الگوریتم بازگشتی چیست؟ – به زبان ساده + مثال و تمرین

سافرادی که علاقه‌مند به برنامه نویسی هستند، در هنگام یادگیری ساختمان داده و طراحی الگوریتم، با مفهوم مهمی به نام «الگوریتم بازگشتی» (Recursive Algorithm) آشنا می‌شوند. این روش برنامه نویسی به شما کمک می‌کند تا برخی مسائل را به‌طور بهینه‌تر و ساده‌تر پیاده‌سازی کنید. در این مطلب از مجله تم آف قصد داریم به این پرسش پاسخ دهیم که الگوریتم بازگشتی چیست و چه ویژگی‌هایی دارد. همچنین، به منظور درک بهتر این مفهوم، مثال‌های ساده و کاربردی برای آن ارائه شده است.

الگوریتم بازگشتی چیست ؟

در الگوریتم بازگشتی، تابعی وجود دارد که به‌طور مستقیم یا غیر مستقیم خودش را تا زمانی فراخوانی می‌کند که شرط توقف تکرار فراخوانی اتفاق نیفتد. الگوریتم بازگشتی در حل مسائلی استفاده می‌شود که بتوان مسئله را به بخش‌های کوچکتری تقسیم کرد و هر یک از این بخش‌های کوچکتر، با تابع اصلی تعریف شده برای مسئله قابل حل باشند. به عبارتی، در طی فرآیند الگوریتم بازگشتی، خروجی‌های بخش‌های کوچکتر مسئله محاسبه و سپس مسئله اصلی، با استفاده از خروجی‌های حاصل شده حل می‌شود.

کاربرد الگوریتم بازگشتی چیست ؟

با استفاده از الگوریتم بازگشتی می‌توان از قطعه کدهای کمتری برای حل مسائل استفاده کرد. به این ترتیب، نوشتن برنامه ساده‌تر انجام می‌شود. این ویژگی به خوانایی برنامه نیز کمک بسزایی می‌کند. همچنین، این الگوریتم برای حل مسائلی مناسب است که روال حل بخش‌های کوچکتر مسئله، همانند مسئله اصلی باشد. محاسبه فاکتوریل و محاسبه n-امین عدد فیبوناچی به عنوان مسائلی محسوب می‌شوند که می‌توان آن‌ها را به‌راحتی با الگوریتم بازگشتی پیاده‌سازی کرد.

ساختار الگوریتم بازگشتی چیست ؟

به منظور پیاده‌سازی الگوریتم بازگشتی، در ابتدا باید مسئله را به ۲ بخش تقسیم کنیم که در ادامه به آن‌ها اشاره شده است:

• وضعیت نهایی: وضعیت نهایی الگوریتم بازگشتی باعث متوقف شدن اجرای الگوریتم می‌شود. چنانچه شرایطی را برای وضعیت نهایی الگوریتم مشخص نکنیم، الگوریتم بازگشتی به دفعات نامتناهی اجرا می‌شود.
• مرحله تکرار: این بخش از الگوریتم بازگشتی باعث فراخوانی مجدد تابع بازگشتی می‌شود و این روند تکرار آنقدر ادامه پیدا می‌کند که به وضعیت نهایی برسیم و الگوریتم متوقف شود. با هر بار فراخوانی تابع بازگشتی، به وضعیت نهایی نزدیک می‌شویم.

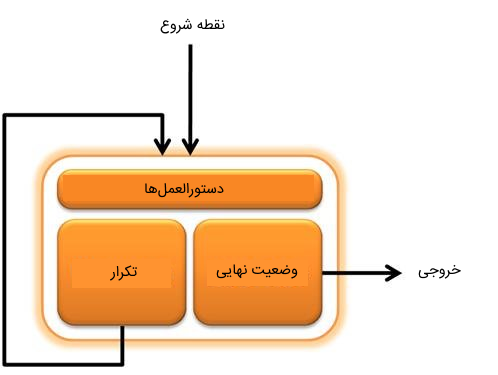
در بخش‌های بعدی مطلب، مثال‌هایی از الگوریتم بازگشتی ارائه شده است که به درک مفاهیم این بخش کمک می‌کنند.

مثال فیبوناچی با الگوریتم بازگشتی

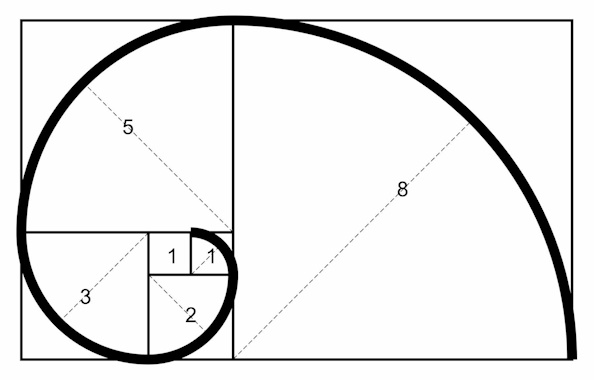
یکی از مثال‌هایی که می‌توانیم برای الگوریتم بازگشتی ارائه کنیم، دنباله فیبوناچی است. در مسئله فیبوناچی به دنبال یافتن مقدار عددی موقعیت n-ام از یک سری اعداد هستیم. سری اعداد فیبوناچی با ۲ عدد ۰ و ۱ شروع می‌شوند و به منظور یافتن مقدار عددی n-ام از این سری، باید n-1 عدد قبلی را با یکدیگر جمع کنیم.

برای حل این مسئله می‌توان ۲ بخش از ساختار الگوریتم بازگشتی را به این نحو تعریف کرد:

• وضعیت نهایی: اگر n برابر با عدد ۱ باشد، تابع فیبوناچی باید مقدار ۰ را برگرداند، زیرا اولین عدد از سری فیبوناچی برابر با ۰ است. چنانچه مقدار n برابر با عدد ۲ باشد، تابع فیبوناچی باید مقدار ۱ را در خروجی ارائه دهد، زیرا دومین عدد از سری فیبوناچی برابر با عدد ۱ است.
• مرحله تکرار: چنانچه مقدار n برابر با هر عددی به جز اعداد ۰ و ۱ باشد، با استفاده از دستور fibonacci(n-1) + fibonacci(n-2)

   می‌توان مقدار عددی سری فیبوناجی را در موقعیت n-ام مشخص کرد.

در ادامه، به نحوه پیاده‌سازی مسئله فیبوناچی با چند زبان برنامه نویسی خواهیم پرداخت.

پیاده سازی مسئله فیبوناچی با الگوریتم بازگشتی در زبان پایتون

در قطعه کد زیر، نحوه پیاده‌سازی مسئله فیبوناچی را با استفاده از الگوریتم بازگشتی در زبان برنامه نویسی پایتون ملاحظه می‌کنید.

def fibonacci(n):
# Python code to implement Fibonacci series
 
# Function for fibonacci
def fib(n):
 
    # Stop condition
    if (n == 0):
        return 0
 
    # Stop condition
    if (n == 1 or n == 2):
        return 1
 
    # Recursion function
    else:
        return (fib(n - 1) + fib(n - 2))

# Driver Code
 
# Initialize variable n.
n = 5;
print("Fibonacci series of 5 numbers is :",end=" ")
 
# for loop to print the fibonacci series.
for i in range(0,n):
    print(fib(i),end=" ")

خروجی قطعه کد بالا در ادامه ملاحظه می‌شود.

Fibonacci series of 5 numbers is: 0 1 1 2 3 

پیاده سازی مسئله فیبوناچی با الگوریتم بازگشتی در زبان C++‎

در قطعه کد زیر، نحوه پیاده‌سازی مسئله فیبوناچی را با استفاده از الگوریتم بازگشتی در زبان برنامه نویسی C++‎ ملاحظه می‌کنید.

// C++ code to implement Fibonacci series
#include 
using namespace std;
 
// Function for fibonacci
 
int fib(int n)
{
    // Stop condition
    if (n == 0)
        return 0;
 
    // Stop condition
    if (n == 1 || n == 2)
        return 1;
 
    // Recursion function
    else
        return (fib(n - 1) + fib(n - 2));
}
 
// Driver Code
int main()
{
    // Initialize variable n.
    int n = 5;
    cout

خروجی حاصل شده از قطعه کد بالا در ادامه ارائه شده است.

Fibonacci series of 5 numbers is: 0 1 1 2 3 

پیاده سازی مسئله فیبوناچی با الگوریتم بازگشتی در زبان C

کد زیر، نحوه پیاده‌سازی مسئله فیبوناچی را با استفاده از الگوریتم بازگشتی در زبان برنامه نویسی C نشان می‌دهد.

// C code to implement Fibonacci series
#include 
 
// Function for fibonacci
int fib(int n)
{
    // Stop condition
    if (n == 0)
        return 0;
 
    // Stop condition
    if (n == 1 || n == 2)
        return 1;
 
    // Recursion function
    else
        return (fib(n - 1) + fib(n - 2));
}
 
// Driver Code
int main()
{
    // Initialize variable n.
    int n = 5;
    printf("Fibonacci series "
           "of %d numbers is: ",
           n);
 
    // for loop to print the fibonacci series.
    for (int i = 0; i 

خروجی قطعه کد بالا در ادامه آمده است.

Fibonacci series of 5 numbers is: 0 1 1 2 3 

پیاده سازی مسئله فیبوناچی با الگوریتم بازگشتی در زبان جاوا

کد زیر، نحوه پیاده‌سازی مسئله فیبوناچی را با استفاده از الگوریتم بازگشتی در زبان برنامه نویسی جاوا را نشان می‌دهد.

// Java code to implement Fibonacci series
import java.util.*;
 
class GFG
{
 
// Function for fibonacci
static int fib(int n)
{
    // Stop condition
    if (n == 0)
        return 0;
 
    // Stop condition
    if (n == 1 || n == 2)
        return 1;
 
    // Recursion function
    else
        return (fib(n - 1) + fib(n - 2));
}
 
// Driver Code
public static void main(String []args)
{
   
    // Initialize variable n.
    int n = 5;
    System.out.print("Fibonacci series of 5 numbers is: ");
 
    // for loop to print the fibonacci series.
    for (int i = 0; i 

خروجی قطعه کد بالا در ادامه ارائه شده است..

Fibonacci series of 5 numbers is: 0 1 1 2 3 

پیاده سازی مسئله فیبوناچی با الگوریتم بازگشتی در سی شارپ

در قطعه کد زیر، نحوه پیاده‌سازی مسئله فیبوناچی را با استفاده از الگوریتم بازگشتی در زبان برنامه نویسی C#‌‎ ملاحظه می‌کنید.

using System;
 
public class GFG
{
 
  // Function for fibonacci
  static int fib(int n)
  {
 
    // Stop condition
    if (n == 0)
      return 0;
 
    // Stop condition
    if (n == 1 || n == 2)
      return 1;
 
    // Recursion function
    else
      return (fib(n - 1) + fib(n - 2));
  }
 
  // Driver Code
  static public void Main ()
  {
 
    // Initialize variable n.
    int n = 5;
    Console.Write("Fibonacci series of 5 numbers is: ");
 
    // for loop to print the fibonacci series.
    for (int i = 0; i 

خروجی قطعه کد بالا در زیر ارائه شده است.

Fibonacci series of 5 numbers is: 0 1 1 2 3 

پیاده سازی مسئله فیبوناچی با الگوریتم بازگشتی در جاوا اسکریپت

قطعه کد زیر، نحوه پیاده‌سازی مسئله فیبوناچی را با استفاده از الگوریتم بازگشتی در زبان برنامه نویسی جاوا اسکریپت نشان می‌دهد.

// JavaScript code to implement Fibonacci series
 
// Function for fibonacci
function fib(n)
{
   // Stop condition
   if(n == 0)
     return 0;
    
   // Stop condition
   if(n == 1 || n == 2)
      return 1;
   // Recursion function
   else
      return fib(n-1) + fib(n-2);
}
 
// Initialize variable n.
let n = 5;
 
document.write("Fibonacci series of 5 numbers is: ");
 
// for loop to print the fibonacci series.
for(let i = 0; i 

خروجی قطعه کد بالا در ادامه آمده است.

Fibonacci series of 5 numbers is: 0 1 1 2 3 

مثال فاکتوریل با استفاده از تابع بازگشتی

محاسبه فاکتوریل نیز از دیگر مسائلی است که می‌توان آن را با استفاده از الگوریتم بازگشتی پیاده‌سازی کرد. فاکتوریل عدد n از محاسبه حاصل ضرب اعداد ۱ تا n محاسبه می‌شود. فاکتوریل عدد ۰ برابر با ۱ است و برای اعداد منفی نیز مقدار فاکتوریل تعریف نمی‌شود.

برای پیاده‌سازی مسئله فاکتوریل با استفاده از الگوریتم بازگشتی می‌توان تابعی تعریف کرد که عدد n را به عنوان آرگومان دریافت می‌کند و در خروجی مقدار فاکتوریل را برمی‌گرداند. برای حل مسئله فاکتوریل نیز می‌توان ۲ بخش اصلی الگوریتم بازگشتی را به شکل زیر مشخص کرد:

• وضعیت نهایی: اگر عدد n برابر با ۰ یا ۱ بود، عدد ۱ را به عنوان خروجی تابع فاکتوریل برمی‌گردانیم. چنانچه عدد n کوچکتر از ۰ باشد، تابع باید خطایی را در خروجی نشان دهد.
• مرحله تکرار: با استفاده از دستور n * factorial(n-1)

   می‌توان ضرب مقادیر ۱ تا n را محاسبه کرد.

در ادامه این مطلب از مجله تم آف، به نحوه پیاده‌سازی مسئله فاکتوریل با استفاده از روش بازگشتی در چندین زبان برنامه نویسی می‌پردازیم.

پیاده سازی مسئله فاکتوریل با الگوریتم بازگشتی در پایتون

در قطعه کد زیر، نحوه پیاده‌سازی مسئله فاکتوریل با استفاده از الگوریتم بازگشتی با زبان پایتون ارائه شده است.

def factorial(n):
# Python3 code to implement factorial
 
# Factorial function
def f(n):
 
    # Stop condition
    if (n == 0 or n == 1):
        return 1;
 
    # Recursive condition
    else:
        return n * f(n - 1);
 
 
# Driver code
if __name__=='__main__':
 
    n = 5;
    print("factorial of",n,"is:",f(n))

خروجی قطعه کد بالا را در ادامه آمده است.

factorial of 5 is: 120

پیاده سازی مسئله فاکتوریل با الگوریتم بازگشتی در C++‎

در قطعه کد زیر، نحوه پیاده‌سازی مسئله فاکتوریل را با استفاده از الگوریتم بازگشتی در زبان برنامه نویسی C++‎ ملاحظه می‌کنید.

// C++ code to implement factorial
#include 
using namespace std;
 
// Factorial function
int f(int n)
{
    // Stop condition
    if (n == 0 || n == 1)
        return 1;
 
    // Recursive condition
    else
        return n * f(n - 1);
}
 
// Driver code
int main()
{
    int n = 5;
    cout

خروجی قطعه کد بالا را در ادامه مشاهده می‌کنید.

factorial of 5 is: 120

پیاده سازی مسئله فاکتوریل با روش بازگشتی در زبان C‎

قطعه کد زیر، نحوه پیاده‌سازی مسئله فاکتوریل را با استفاده از الگوریتم بازگشتی در زبان برنامه نویسی C‎ نشان می‌دهد.

// C code to implement factorial
#include 
 
// Factorial function
int f(int n)
{
    // Stop condition
    if (n == 0 || n == 1)
        return 1;
 
    // Recursive condition
    else
        return n * f(n - 1);
}
 
// Driver code
int main()
{
    int n = 5;
    printf("factorial of %d is: %d", n, f(n));
    return 0;
}

خروجی قطعه کد بالا در ادامه ملاحظه می‌شود.

factorial of 5 is: 120

پیاده سازی مسئله فاکتوریل با روش بازگشتی در جاوا

در ادامه، نحوه پیاده‌سازی مسئله فاکتوریل را با استفاده از الگوریتم بازگشتی در زبان برنامه نویسی جاوا‎ را ملاحظه می‌کنید.

// Java code to implement factorial
public class GFG
{
 
  // Factorial function
  static int f(int n)
  {
 
    // Stop condition
    if (n == 0 || n == 1)
      return 1;
 
    // Recursive condition
    else
      return n * f(n - 1);
  }
 
  // Driver code
  public static void main(String[] args)
  {
    int n = 5;
    System.out.println("factorial of " + n + " is: " + f(n));
  }
}

خروجی قطعه کد بالا در ادامه ارائه شده است.

factorial of 5 is: 120

پیاده سازی مسئله فاکتوریل با روش بازگشتی در سی شارپ

کد زیر، نحوه پیاده‌سازی مسئله فاکتوریل را با استفاده از الگوریتم بازگشتی در زبان برنامه نویسی C‎#‎ را نشان می‌دهد.

// C# code to implement factorial
using System;
class GFG {
 
  // Factorial function
  static int f(int n)
  {
    // Stop condition
    if (n == 0 || n == 1)
      return 1;
 
    // Recursive condition
    else
      return n * f(n - 1);
  }
 
  // Driver code
  static void Main()
  {
    int n = 5;
    Console.WriteLine("factorial of " + n + " is: " + f(n));
  }
}
 

خروجی حاصل شده از قطعه کد بالا را در زیر ملاحظه می‌کنید.

factorial of 5 is: 120

پیاده سازی مسئله فاکتوریل با تابع بازگشتی در جاوا اسکریپت‎

در قطعه کد زیر، نحوه پیاده‌سازی مسئله فاکتوریل با استفاده از الگوریتم بازگشتی در زبان برنامه نویسی جاوا اسکریپت ارائه شده است.

// JavaScript code to implement factorial
 
// Factorial function
function f(n)
{
   // Stop condition
   if(n == 0 || n == 1)
     return 1;
      
   // Recursive condition
   else
      return n*f(n-1);
}
 
// Initialize variable n.
let n = 5;
document.write("factorial of "+ n +" is: " + f(n));

خروجی قطعه کد بالا را در زیر ملاحظه می‌کنید.

factorial of 5 is: 120

انواع بازگشت در الگوریتم بازگشتی

در الگوریتم بازگشتی، می‌توان به حالت‌های مختلف، تابع بازگشتی را فراخوانی کرد.

در ادامه، به انواع روش‌های بازگشتی اشاره شده است.

• فراخواندن تابع «بازگشتی به‌طور مستقیم» (Direct Recursion)
• فراخوانی تابع «بازگشتی به‌طور غیر مستقیم» (Indirect Recursion)
• روش «بازگشتی دنباله‌دار» (Tailed Recursion)

در بخش بعدی این مطلب از مجله تم آف، به شرح هر یک از روش‌های فراخوانی تابع بازگشتی پرداخته شده است.

الگوریتم بازگشتی مستقیم

در الگوریتم‌های بازگشتی مستقیم، نام تابع بازگشتی، درون تابع به طور مستقیم فراخوانی می‌شود. در ادامه، مثالی از این نوع الگوریتم بازگشتی را ملاحظه می‌کنید.

// An example of direct recursion
void directRecFun()
{
    // Some code....

    directRecFun();

    // Some code...
}

الگوریتم بازگشتی غیر مستقیم

در الگوریتم‌های بازگشتی غیر مستقیم، فراخوانی مکرر تابع توسط تابع دیگر انجام می‌شود. در ادامه، مثالی از الگوریتم بازگشتی غیر مستقیم آمده است. در این مثال، توابع void indirectRecFun1

 و void indirectRecFun2

 از نوع بازگشتی هستند که یکدیگر را فرا می‌خوانند.

// An example of indirect recursion
void indirectRecFun1()
{
    // Some code...

    indirectRecFun2();

    // Some code...
}
void indirectRecFun2()
{
    // Some code...

    indirectRecFun1();

    // Some code...
}

الگوریتم بازگشتی دنباله دار چیست؟

در الگوریتم بازگشتی دنباله‌دار، نیازی به حافظه «پشته» (Stack) برای نگهداری مقادیر حاصل شده از فراخوانی قبلی تابع وجود ندارد. به عبارتی، در این روش، ابتدا محاسبات لازم انجام و سپس تابع بازگشتی فراخوانده می‌شود.

به منظور درک بهتر عملکرد این نوع الگوریتم، می‌توان از مثالی کمک گرفت. فرض کنید می‌خواهیم حاصل جمع اعداد ۱ تا n را محاسبه کنیم. برای حل این مسئله، می‌توان از ۲ روش بازگشتی ساده و دنباله‌دار استفاده کرد. در قطعه کد زیر، از روش بازگشتی ساده برای حل این مسئله به زبان جاوا استفاده شده است.

public int sumTo(int x) {
    if (x == 1) {
        return x;
    } else {
        return x + sumTo(x - 1);
    }
}

همان‌طور که در قطعه کد بالا ملاحظه می‌شود، برای محاسبه حاصل جمع نهایی، نیاز است نتایج فراخوانی‌های قبلی در پشته ذخیره شوند. نحوه محاسبه مقادیر این تابع در ادامه آمده است.

sumTo(5)
5 + sumTo(4)
5 + (4 + sumTo(3))
5 + (4 + (3 + sumTo(2)))
5 + (4 + (3 + (2 + sumTo(1))))
5 + (4 + (3 + (2 + 1)))
15

بر خلاف روش قبل، در الگوریتم بازگشتی دنباله‌دار، عملیات محاسبات در ابتدا انجام می‌شود و سپس تابع بازگشتی فراخوانده خواهد شد. در قطعه کد زیر، مثال قبل با الگوریتم بازگشتی دنباله‌دار با زبان جاوا پیاده‌سازی شده است.

public int tailRecSumTo(int x, int total) {
    if (x == 0) {
        return total;
    } else {
        return tailRecSumTo(x - 1, total + x);
    }
}

نحوه محاسبه حاصل جمع نهایی بر اساس قطعه کد بالا به صورت زیر است.

tailRecSumTo(5, 0)
tailRecSumTo(4, 5)
tailRecSumTo(3, 9)
tailRecSumTo(2, 12)
tailRecSumTo(1, 14)
tailRecSumTo(0, 15)
15

همان‌طور که ملاحظه می‌شود،‌ در هر مرحله، محاسبات جمع انجام می‌شود و نیازی به نگهداری تمام مقادیر ورودی تابع در حافظه نیست.

مزایای تابع بازگشتی چیست ؟

روش بازگشتی در برنامه نویسی دارای مزیت‌های مهمی است و همین امر باعث شده است در حل مسائل مختلفی از آن استفاده شود. در ادامه، به برخی از مهم‌ترین مزیت‌های الگوریتم بازگشتی اشاره شده است.

• ساده‌سازی مسائل پیچیده: با استفاده از الگوریتم بازگشتی می‌توان مسائل پیچیده را به بخش‌های کوچک‌تر تقسیم کرد تا پیاده‌سازی آن‌ها ساده‌تر شود.
• مدیریت بهتر زمان و حافظه: از آنجایی که الگوریتم بازگشتی باعث کاهش حجم کد نویسی می‌شود، نقش بسزایی در کاهش زمان پردازش و میزان مصرف حافظه دارد.
• افزایش میزان خوانایی برنامه: الگوریتم بازگشتی نقش مهمی در ساده کردن برنامه نویسی دارد. همین امر باعث افزایش میزان خوانایی برنامه می‌شود.
• بهبود پردازش داده: با استفاده از روش بازگشتی می‌توان عملیات ذخیره و بازیابی اطلاعات در حافظه را بهبود داد. از این الگوریتم می‌توان برای پیمایش ساختمان داده‌هایی نظیر درخت و گراف به آسانی استفاده کرد.

معایب روش بازگشتی چیست ؟

الگوریتم بازگشتی علیرغم مزیت‌های مهمی که دارد، دارای معایبی نیز هست که در ادامه به مهم‌ترین آن‌ها اشاره می‌کنیم.

• پر شدن حافظه پشته: در هنگام استفاده از روش بازگشتی ممکن است با خطای پر بودن پشته مواجه شویم. این رویداد زمانی اتفاق می‌افتد که تابع بازگشتی به دفعات زیادی فراخوانده شود.
• ابهام در درک و خطایابی برنامه: در مسائل پیچیده ممکن است درک و خطایابی برنامه دشوار باشد. به عنوان مثال ممکن است در توابع بازگشتی، چندین حالت توقف در نظر بگیریم که همین امر باعث می‌شود تشخیص نقطه توقف تابع دشوار شود.
• سرعت اجرای پایین برنامه: با فراخوانی مکرر توابع بازگشتی، ارسال پارامترها به تابع و به‌روزرسانی حافظه پشته اتفاق می‌افتند. این امر سبب می‌شود سرعت اجرای این توابع پایین بیاید.
• استفاده از روش بازگشتی در مسائل محدود: از الگوریتم بازگشتی صرفاً می‌توان در برخی مسائل خاص استفاده کرد.

جمع‌بندی

الگوریتم بازگشتی یکی از مفاهیم مهم برنامه نویسی است و از آن می‌توان برای ساده‌تر کردن پیاده‌سازی برخی مسائل پیچیده استفاده کرد. این روش از برنامه نویسی بر پایه ۲ مفهوم وضعیت نهایی و مرحله تکرار عمل می‌کند که همین ۲ ویژگی باعث می‌شوند خوانایی و درک برنامه بیشتر شود. در مطلب فعلی از مجله تم آف سعی داشتیم با زبان ساده به این پرسش‌ها پاسخ دهیم که الگوریتم بازگشتی چیست و مزایا و معایب آن چه هستند. همچنین، با ارائه مثال‌های کاربردی، نحوه عملکرد این روش را توضیح دادیم.