کار با داده های مالی در پایتون — راهنمای مقدماتی

به دلیل اهمیت و کاربرد بالای دادههای مالی، بررسی عمیقتر آنها برای فهم بهترشان امری ضروری است. دادههای مالی میتواند شامل سریهای زمانی و سایر دادهها شود. در این مطلب به آموزش مقدماتی کار با داده های مالی در پایتون خواهیم پرداخت. این دادهها از نوع سریهای زمانی شامل تاریخچه قیمت برخی نمادها هستند.

کتابخانه های مورد نیاز برای کار با داده های مالی در پایتون
وارد محیط برنامهنویسی پایتون شده و کتابخانههای مورد نیاز را فراخوانی میکنیم:
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
import statsmodels.graphics.tsaplots as tsapltاین کتابخانهها به ترتیب برای موارد زیر استفاده خواهند شد:
- کار با آرایهها و محاسبات برداری
- کار با دیتافریمها و فایلهای داده
- دریافت دادههای مالی به صورت آنلاین از طریف API مربوط به Yahoo Finance
- رسم نمودار
- رسم نمودارهای خودهمبستگی
تنظیمات مربوط به برخی کتابخانهها را نیز بهشکل زیر مینویسیم:
np.random.seed(0)
plt.style.use('ggplot')برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
دریافت آنلاین داده از API
برای دریافت اطلاعات مربوط به تاریخچه قیمت، از API (مخفف Application Programming Interface) مربوط به Yahoo Finance استفاده خواهیم کرد. به این منظور، بهشکل زیر نماد مورد نظر را تعریف میکنیم:
Ticker = yf.Ticker('GLD')در این سطر از اسم اختصار GLD که مربوط به طلا است استفاده میکنیم.
حال میتوانیم تاریخچه را با استفاده از متد history دریافت کنیم:
DF = Ticker.history(interval='1d', start='2017-01-01', end='2022-01-01')این متد در خروجی یک دیتافریم برمیگرداند. توجه داشته باشید که ورودیهای بیشتری نیز برای این متد قابل تعریف است که برخی مهمترینها در زیر آورده شدهاند:
- period: این ورودی نشاندهنده مدت زمان مورد درخواست است.
- interval: این ورودی نشاندهنده تایم فریم ثبت داده است.
- start: این ورودی تاریخ اولین رکورد را تعیین میکند.
- end: این ورودی تاریخ آخرین رکورد را تعیین میکند.
- tz: این ورودی منطقه زمانی (Time Zone) مورد نظر برای داده را تعیین میکند.
حال برای مشاهده ۱۰ سطر اول دیتافریم دریافتشده، بهشکل زیر عمل میکنیم:
print(DF.head(10))که در خروجی خواهیم داشت:
Open High Low Close Volume Dividends Stock Splits Date 2017-01-03 109.620003 111.000000 109.370003 110.470001 7527400 0 0 2017-01-04 111.059998 111.220001 110.610001 110.860001 4904100 0 0 2017-01-05 112.160004 112.940002 112.070000 112.580002 9606800 0 0 2017-01-06 111.809998 112.379997 111.570000 111.750000 7686100 0 0 2017-01-09 112.389999 113.040001 112.180000 112.669998 5674600 0 0 2017-01-10 112.940002 113.449997 112.639999 113.150002 6093400 0 0 2017-01-11 112.870003 114.190002 112.169998 113.500000 9918700 0 0 2017-01-12 114.519997 114.930000 113.809998 113.910004 8457300 0 0 2017-01-13 113.650002 114.309998 113.190002 114.209999 7261500 0 0 2017-01-17 115.889999 115.959999 115.500000 115.849998 9142400 0 0
به این ترتیب، مشاهده میکنیم که داده بهدرستی دریافت شده و شامل ستونهای زیر است:
- Date: تاریخ هر سطر از داده را نشان میدهد.
- Open: اولین قیمت مشاهدهشده در روز مربوطه را نشان میدهد.
- High: بیشترین قیمت مشاهدهشده در روز مربوطه را نشان میدهد.
- Low: کمترین قیمت مشاهدهشده در روز مربوطه را نشان میدهد.
- Close: آخرین قیمت مشاهدهشده در روز مربوطه را نشان میدهد. توجه داشته باشید که در برخی از بازارها، قیمت Close میانگینی وزندار از معاملات آن روز است و از قیمت Last به عنوان آخرین قیمت مشاهده شده استفاده میشود.
- Volume: تعداد و حجم معاملات در روز مربوطه را نشان میدهد.
در ادامه، دیتافریم دو ستون اضافه نیز وجود دارد که خالی میباشند به همین دلیل، آنها را بهشکل زیر حذف میکنیم:
DF.drop(['Dividends', 'Stock Splits'], axis=1, inplace=True)پس از اعمال کد فوق، دیتافریم بهصورت زیر خواهد بود:
Open High Low Close Volume Date 2017-01-03 109.620003 111.000000 109.370003 110.470001 7527400 2017-01-04 111.059998 111.220001 110.610001 110.860001 4904100 2017-01-05 112.160004 112.940002 112.070000 112.580002 9606800 2017-01-06 111.809998 112.379997 111.570000 111.750000 7686100 2017-01-09 112.389999 113.040001 112.180000 112.669998 5674600 2017-01-10 112.940002 113.449997 112.639999 113.150002 6093400 2017-01-11 112.870003 114.190002 112.169998 113.500000 9918700 2017-01-12 114.519997 114.930000 113.809998 113.910004 8457300 2017-01-13 113.650002 114.309998 113.190002 114.209999 7261500 2017-01-17 115.889999 115.959999 115.500000 115.849998 9142400
به این ترتیب، ستونهای اضافه حذف میشوند.
حال میتوانیم درصد تغییرات قیمت در هر روز معاملاتی را محاسبه و در یک ستون جدید وارد دیتافریم کنیم.
درصد تغییرات قیمت بهصورت زیر قابل محاسبه است:
$$text { Relative Change }(%)=100 times frac{text { Close }-text { Open }}{text { Open }}=100 timesleft(frac{text { Close }}{text { Open }}-1right) $$
برای این منظور، میتوانیم بنویسیم:
DF['Return'] = 100 * (DF['Close'] / DF['Open'] - 1)پس از اعمال کد فوق، دیتافریم بهصورت زیر درمیآید:
Open High Low Close Volume Return Date 2017-01-03 109.620003 111.000000 109.370003 110.470001 7527400 0.775405 2017-01-04 111.059998 111.220001 110.610001 110.860001 4904100 -0.180080 2017-01-05 112.160004 112.940002 112.070000 112.580002 9606800 0.374463 2017-01-06 111.809998 112.379997 111.570000 111.750000 7686100 -0.053660 2017-01-09 112.389999 113.040001 112.180000 112.669998 5674600 0.249131 2017-01-10 112.940002 113.449997 112.639999 113.150002 6093400 0.185939 2017-01-11 112.870003 114.190002 112.169998 113.500000 9918700 0.558162 2017-01-12 114.519997 114.930000 113.809998 113.910004 8457300 -0.532652 2017-01-13 113.650002 114.309998 113.190002 114.209999 7261500 0.492739 2017-01-17 115.889999 115.959999 115.500000 115.849998 9142400 -0.034516
به این ترتیب، ستون مربوط به درصد تغییرات قیمت به دیتافریم اضافه میشود.
رسم برخی نمودارهای مهم
ابتدا نمودار مربوط به قیمت Close را رسم میکنیم تا تغییرات قیمت نشان داده شود. برای این منظور، مینویسیم:
plt.plot(DF['Close'])
plt.show()در خروجی کد فوق، نمودار زیر حاصل میشود:
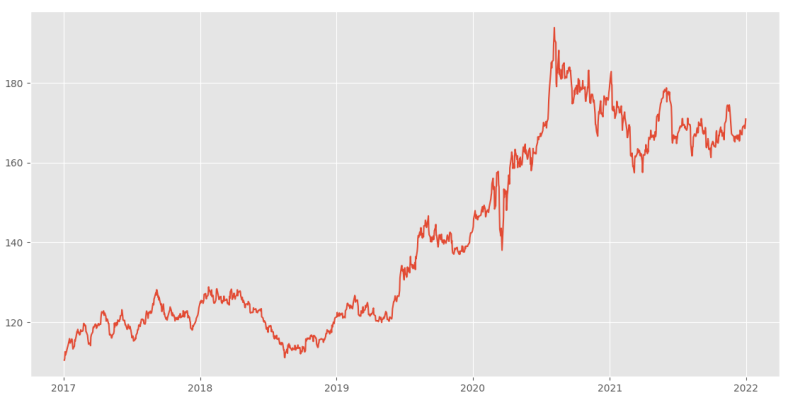
به این ترتیب، مشاهده میکنیم که نمودار قیمت در مقابل زمان رسم شده است. این نمودار مشکلاتی دارد، برای مثال بهتر است از نمودار نیمه لگاریتمی (Semi-Logarithm) استفاده کنیم:
plt.semilogy(DF['Close'])
plt.show()در خروجی، تصویر زیر را خواهیم داشت.
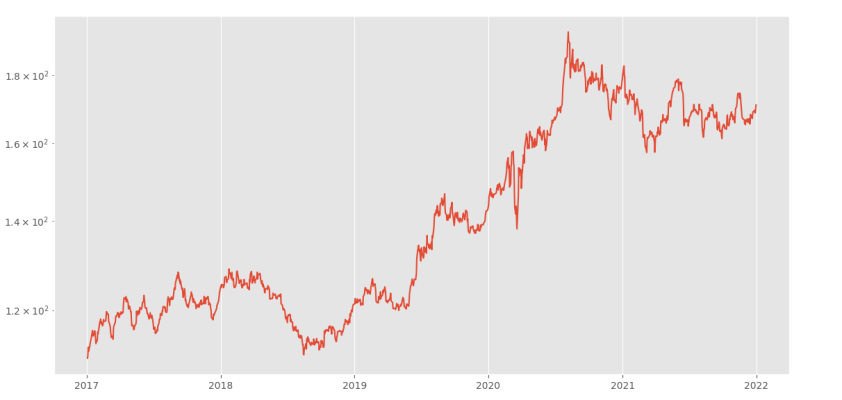
به این ترتیب، نمودار حاصل روند، سطوح حمایت و سطوح مقاومت را به خوبی نشان میدهد.
بهتر است یک عنوان برای نمودار Title و برچسبهایی برای محورها Xlabel & Ylabel تعیین کنیم. کاهش ضخامت خط نمودار نیز میتواند جزئیات نمودار را بهتر نشان دهد:
plt.semilogy(DF['Close'], lw=0.9)
plt.title('Gold Price Over Last 5 Years')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.show()که شکل زیر را خواهیم داشت.
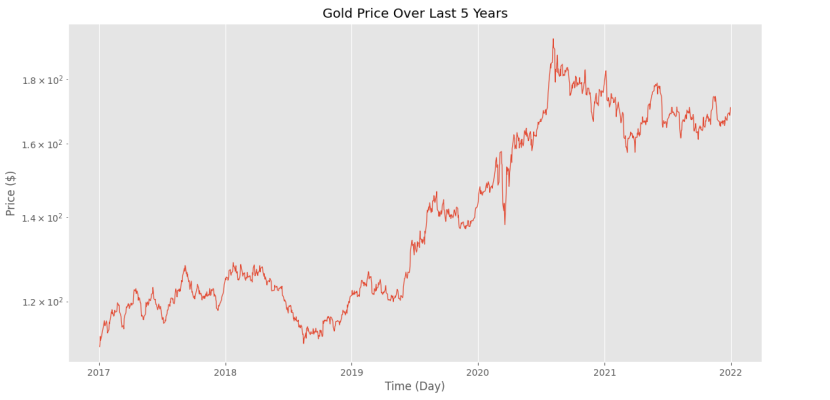
به این ترتیب، نمودار مد نظر رسم میشود و بهخوبی اطلاعات مربوط به قیمت را نشان میدهد.
میتوانیم نمودار دیگری نیز برای درصد تغییرات قیمت رسم کنیم:
plt.plot(DF['Return'], lw=0.9)
plt.title('Gold Return Over Last 5 Years')
plt.xlabel('Time (Day)')
plt.ylabel('Relative Change (%)')
plt.show()که نمودار زیر حاصل خواهد شد.
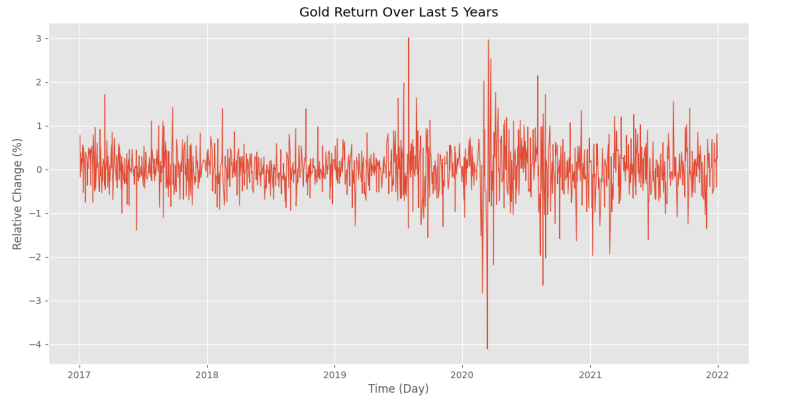
به این ترتیب، مشاهده میکنیم که در اغلب روزها، تغییرات قیمت کمتر از ٪۱ بوده است. برای تشخیص روزهایی با تغییرات قیمت غیرعادی، میتوانیم از دامنه میانچارکی استفاده کنیم.
اگر برای یک متغیر چارکهای اول و سوم را با نماد $$q_1$$ و $$q_3$$ نشان دهیم، دامنه میانچارک بهصورت زیر تعریف میشود:
$$ i q r = q_3 – q _ 1 $$
سپس میتوانیم «حد بالا» (Upper Bound) و «حد پایین» (Lower Bound) را بهشکل زیر تعریف کنیم:
$$ begin{aligned}
&U=q _3+1.5 times i q r=2.5 times q_{3}-1.5 times q_{1} \
&L=q _1-1.5 times i q r=2.5 times q_{1}-1.5 times q_{3}
end{aligned} $$
دادههایی که در خارج از این بازه قرار گیرند، میتوانند بهعنوان ناهنجاری (Anomaly) تشخیص داده شوند. به این منظور، میتوانیم محاسبات لازم را انجام داده و دو خط مربوط به حد بالا و حد پایین را روی نمودار قبلی رسم کنیم:
q1 = DF['Return'].quantile(0.25)
q3 = DF['Return'].quantile(0.75)
iqr = q3 - q1
U = q3 + 1.5 * iqr
L = q1 - 1.5 * iqr
plt.plot(DF['Return'], lw=0.9, label='Return')
plt.plot([DF.index[0], DF.index[-1]], [U, U], lw=1.2, c='k', label='Lower Bound')
plt.plot([DF.index[0], DF.index[-1]], [L, L], lw=1.2, c='k', label='Upper Bound')
plt.title('Gold Return Over Last 5 Years')
plt.xlabel('Time (Day)')
plt.ylabel('Relative Change (%)')
plt.legend()
plt.show()با اجرای کد فوق، نمودار زیر در خروجی نشان داده میشود.
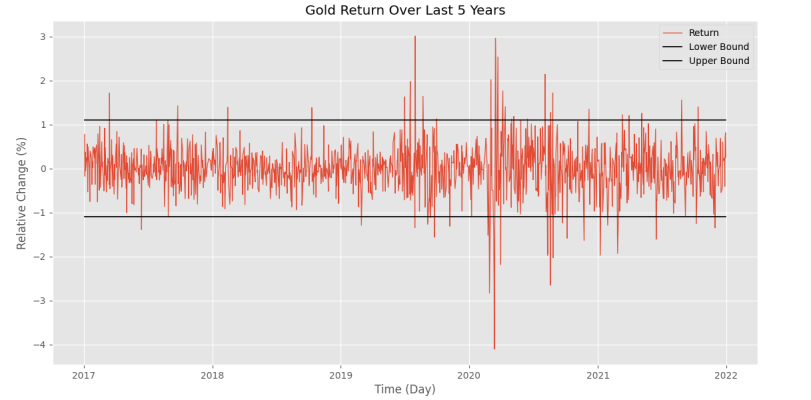
به این ترتیب، روزهای با تغییرات غیرعادی بهخوبی تشخیص داده میشود. در تحلیل سریهای زمانی، بعضاً اصلاح این دادهها از اهمیت بالایی برخوردار است.
میتوانیم حد بالا و پایین را با توجه به میانگین و انحراف معیار نیز تعریف کنیم:
$$ begin{aligned}
M &=frac{1}{n} sum_{i=1}^{n} x_{i} \
S &=sqrt{frac{1}{n} sum_{i=1}^{n}left(x_{i}-Mright)^{2}} \
U &=M+2 times S \
L &=M-2 times S
end{aligned} $$
برای این حالت نیز کدنویسی بهشکل زیر تغییر میکند:
M = DF['Return'].mean()
S = DF['Return'].std()
U = M + 2 * S
L = M - 2 * S
plt.plot(DF['Return'], lw=0.9, label='Return')
plt.plot([DF.index[0], DF.index[-1]], [U, U], lw=1.2, c='k', label='Lower Bound')
plt.plot([DF.index[0], DF.index[-1]], [L, L], lw=1.2, c='k', label='Upper Bound')
plt.title('Gold Return Over Last 5 Years')
plt.xlabel('Time (Day)')
plt.ylabel('Relative Change (%)')
plt.legend()
plt.show()که شکل زیر را خواهیم داشت.
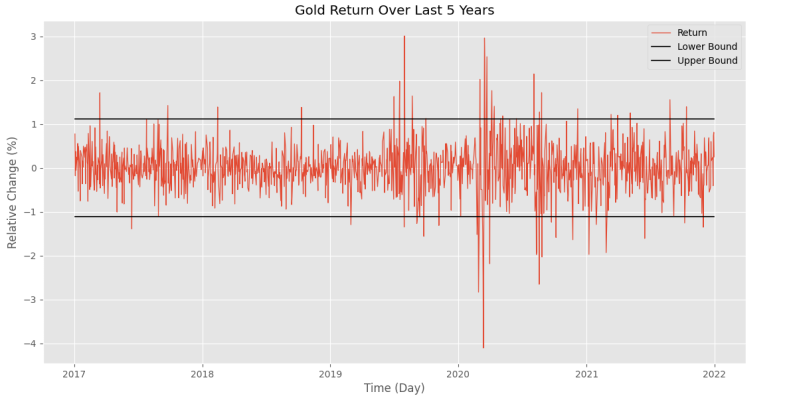
مشاهده میکنیم که تفاوت چندانی با روش قبلی مشاهده نمیشود.
خودهمبستگی قیمت
با توجه به اینکه دادهها از نوع سری زمانی (Time Series) هستند، میتوان همبستگی قیمت با خود را نیز بررسی کرد که خودهمبستگی (Autocorrelation) نام دارد. برای مطالعه بیشتر میتوانید به مطلب «مدل خودهمبسته (Autoregressive) در پایتون – راهنمای گام به گام» مراجعه کنید.
برای رسم نمودار تابع خودهمبستگی (Autocorrelation Function – ACF) میتوانیم بهصورت زیر بنویسیم:
tsaplt.plot_acf(DF['Close'], lags=800, c='teal', lw=0.4, markersize=1)
plt.xlabel('Lags (Days)')
plt.ylabel('Pearson Correlation Coefficient')
plt.show()پس از اجرای کد، نمودار بهصورت زیر حاصل میشود.
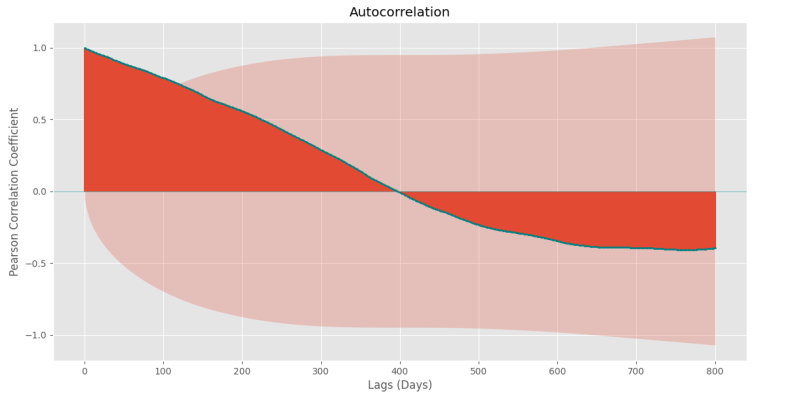
به این ترتیب، مشاهده میکنیم که قیمت طلا با ۱۲۰ روز گذشته رابطه معنادار داشته و با Lag=760 نیز بیشترین رابطه عکس را دارد. از طرفی، نبود هیچگونه همبستگی با Lag=395 نیز بهخوبی قابل مشاهده است.
میتوانیم نمودار تابع خودهمبستگی جزئی (Partial Autocorrelation Function – PACF) را نیز بهشکل زیر رسم کنیم:
tsaplt.plot_pacf(DF['Close'], lags=200, c='teal', lw=0.4, markersize=1)
plt.xlabel('Lags (Days)')
plt.ylabel('Pearson Correlation Coefficient')
plt.show()که نمودار زیر حاصل میشود.
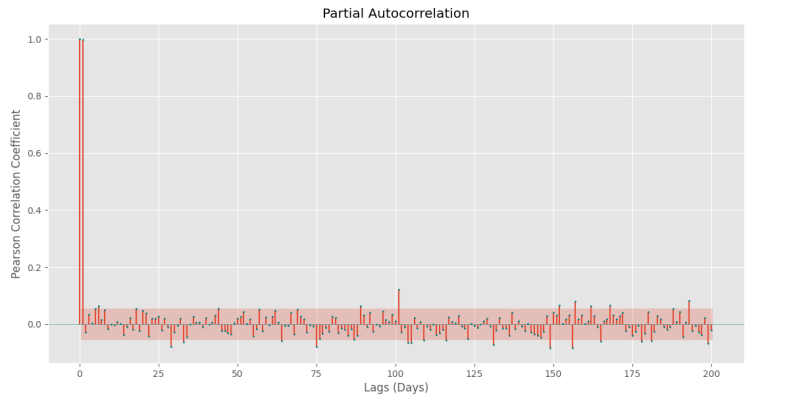
مشاهده میکنیم که قیمت با تأخیرهای زیر رابطه معنادار خوبی دارد:
$$ text {Lags}={0,1,6,29,101,149,156,157,193} $$
به این صورت میتوانیم تأخیرهای مهم را استخراج کنیم و در مدلسازیها استفاده کنیم.
دو نمودار اخیر را برای ستون Return نیز رسم میکنیم که نتایج بهشکل زیر میشود.
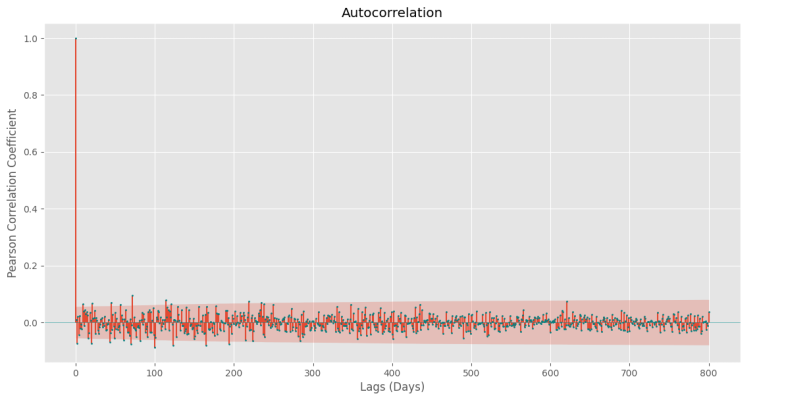
و
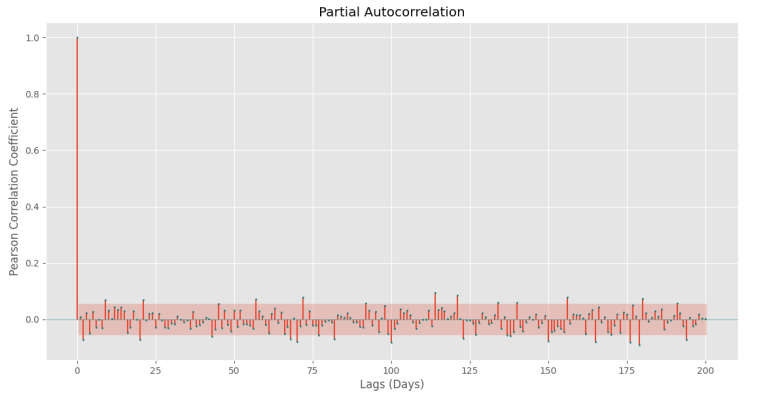
کاملاً مشهود است که تغییرات زیادی در نمودارها ایجاد شده است. به این ترتیب، نشان داده شد که اعمال اپراتور تغییرات نسبی باعث تغییرات زیادی در رفتار و همبستگی سری زمانی میشود. به این دلیل، پیشپردازش اعمالشده روی سری زمانی، در نتایج مدلسازی بسیار تأثیرگذار است.
ذخیره فایل نهایی برای استفادههای بعدی
در صورت استفاده از نمادهای زیاد، دریافت تمامی دادهها در هر بار اجرای الگوریتمها، بهدلیل برخی محدودیتهای API، زمانبر بودن دریافت داده و کمبود منابع سختافزاری، بهتر است تا دادهها را ذخیره کنیم و در دفعات بعدی از فایلهای ذخیرهشده استفاده کنیم.
به این منظور، میتوانیم بهصورت زیر عمل کنیم:
DF.to_csv('GLD.csv', sep=',', encoding='utf-8', index=True)در خروجی این کد، یک فایل CSV در کنار برنامه ایجاد میشود که میتوانید آن را از اینجا (+) دانلود کنید.
به این ترتیب، مجموعه داده نیز ذخیره میشود و در استفادههای بعدی میتوان از آن استفاده کرد.
جمعبندی کار با داده های مالی در پایتون
در این مطلب، به کار با داده های مالی در پایتون از قبیل پردازش، رسم نمودار و تحلیلهای پایه در رابطه با دادههای مالی پرداختیم.
برای مطالعه بیشتر میتوان به پرسشهای زیر پاسخ داد:
- خود همبستگی لگاریتم قیمت به چه صورت است؟
- چگونه میتوان یک مدل خودهمبسته برای پیشبینی تغییرات قیمت ایجاد کرد؟
- ارتباط بین قیمت طلا و نقره به چه صورت است؟
- چگونه میتوان داده روزهای با تغییرات ناهنجار را اصلاح کرد؟

