پیاده سازی میانگین متحرک هال در پایتون — راهنمای گام به گام

در مطالب گذشته مجله تم آف، به روشهای کاهش «تأخیر» (Lag) در میانگینهای متحرک پرداختیم و چندین روش را مشاهده کردیم. در این مطلب میخواهیم به میانگین متحرک هال (Hull Moving Average) یا HMA بپردازیم که تأخیر بسیار کمی دارد و بسیار عالی عمل میکند. به همین منظور، این میانگین متحرک، در بین دیگران، پرطرفدار است.

میانگین متحرک هال
برای محاسبه این میانگین متحرک در پنجره زمانی L، به شکل زیر دو «میانگین متحرک وزندار» (Weighted Moving Average) یا WMA محاسبه میکنیم:
$$ begin{gathered}
W M A_{s}=W M Aleft(X, frac{L}{2}right) \
W M A_{l}=W M A(X, L)
end{gathered} $$
برای آشنایی بیشتر با میانگین متحرک وزندار، میتوانید به مطلب «میانگین متحرک وزن دار در پایتون — راهنمای گام به گام» مراجعه کنید.
به این ترتیب، دو میانگین متحرک کوتاه (Short) و بلند (Long) خواهیم داشت. حال میتوانیم همانند حالتی که در میانگین متحرک دوگانه (Double Exponential Moving Average) یا DEMA داشتیم، اختلاف دو میانگین متحرک وزندار را به میانگین متحرک کوتاه اضافه کنیم:
$$text { Raw HMA }=W M A_{s}+left(W M A_{s}-W M A_{l}right)=2 times W M A_{s}-W M A_{l}$$
به این ترتیب، بخشی از تأخیر با استفاده از میانگین متحرک وزندار رفع میشود. بخشی دیگر از تأخیر نیز با استفاده از طول بازههای مختلف و اصلاح آنها برطرف میشود. برای هموار کردن (Smoothing) خروجی اندیکاتور (Indicator)، بار دیگر میانگین متحرک وزندار را روی خروجی قبلی اعمال میکنیم:
$$H M A=W M A(operatorname{Ram} H M A, sqrt{L}) $$
به این ترتیب، خروجی حاصل هم هموار بوده و هم دارای تأخیر کمتری است.
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
پیاده سازی میانگین متحرک هال در پایتون
برای پیادهسازی این اندیکاتور در پایتون، وارد محیط برنامهنویسی شده و کتابخانههای مورد نیاز فراخوانی میکنیم:
import numpy as np
import yfinance as yf
import matplotlib.pyplot as pltاین سه کتابخانه به ترتیب برای محاسبات برداری، دریافت داده و رسم نمودار استفاده خواهند شد.
تنظیمات کتابخانه Matplotlib را نیز به شکل زیر تعریف میکنیم:
plt.style.use('ggplot')حال دادههای یک سال اخیر مربوط به شرکت Microsoft که با نماد MSFT شناخته میشود را دریافت میکنیم:
Ticker = yf.Ticker('MSFT')
DF = Ticker.history(period='1y', interval='1d')پس از اجرای کد، ۵ سطر ابتدایی را میتوانیم با کد زیر مشاهده کنیم:
print(DF.head())که خروجی به شکل زیر خواهد بود:
Open High Low Close Volume Dividends Stock Splits Date 2021-03-22 228.409512 234.985934 228.280557 234.083298 30127000 0.0 0 2021-03-23 235.571177 239.102411 235.154572 235.660446 31638400 0.0 0 2021-03-24 235.928260 236.077042 233.418703 233.557571 25620100 0.0 0 2021-03-25 233.398890 235.025639 229.699031 230.462799 34061900 0.0 0 2021-03-26 229.679176 234.797489 229.679176 234.569336 25479900 0.0 0
حال میتوان نموداری برای ستون مربوط به قیمت Close رسم کرد:
DF.plot(y='Close',
kind='line',
title='MSFT Last 1 Year Historical Price',
logy=True,
xlabel='Date',
ylabel='Price ($)')
plt.show()که نمودار به شکل زیر خواهد بود.
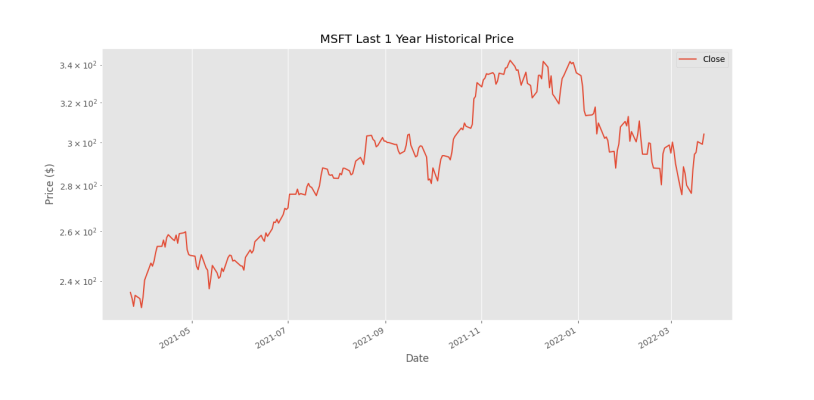
حال میتوانیم میانگین متحرک هال را پیادهسازی کنیم. برای پیادهسازی، نیاز داریم تا تابع مربوط به میانگین متحرک وزندار را از مطالب گذشته وارد کد کنیم:
def WMA(S:np.ndarray, L:int):
W = np.arange(start=1, stop=L+1, step=1)
W = W / W.sum()
nD0 = S.size
nD = nD0 - L + 1
wma = np.zeros(nD)
for i in range(nD):
wma[i] = np.multiply(S[i:i + L], W).sum()
return wmaحال یک تابع با نام HMA ایجاد میکنیم که در ورودی سری زمانی و طول پنجره زمانی را میگیرد:
def HMA(S:np.ndarray, L:int):اکنون طول پنجره برای میانگین متحرکها را محاسبه کنیم:
def HMA(S:np.ndarray, L:int):
lShort = round(L / 2)
lLong = L
lSmooth = round(L**0.5)توجه داشته باشید که چون ممکن است $$ frac {L}2$$ و $$sqrt {L}$$ اعداد طبیعی نباشند، باید از تابع Round برای تبدیل این اعداد به Integer استفاده کنیم.
حال دو میانگین متحرک وزندار کوتاه و بلند را محاسبه میکنیم:
def HMA(S:np.ndarray, L:int):
lShort = round(L / 2)
lLong = L
lSmooth = round(L**0.5)
sWMA = WMA(S, lShort)
lWMA = WMA(S, lLong)حال میتوانیم Raw HMA را محاسبه کنیم. برای محاسبه، باید طول دو میانگین متحرک وزندار با یکدیگر برابر باشد، برای این منظور، به شکل زیر عمل میکنیم:
def HMA(S:np.ndarray, L:int):
lShort = round(L / 2)
lLong = L
lSmooth = round(L**0.5)
sWMA = WMA(S, lShort)
lWMA = WMA(S, lLong)
sWMA = sWMA[-lWMA.size:]حال رابطه مربوط به Raw HMA را اعمال میکنیم:
def HMA(S:np.ndarray, L:int):
lShort = round(L / 2)
lLong = L
lSmooth = round(L**0.5)
sWMA = WMA(S, lShort)
lWMA = WMA(S, lLong)
sWMA = sWMA[-lWMA.size:]
rawHMA = 2 * sWMA - lWMAبه این ترتیب HMA خام محاسبه میشود. برای جلوگیری از رفتارهای شدید و نوسان زیاد، بار دیگر میانگین متحرک وزندار را به شکل زیر اعمال میکنیم و خروجی تابع حاصل میشود:
def HMA(S:np.ndarray, L:int):
lShort = round(L / 2)
lLong = L
lSmooth = round(L**0.5)
sWMA = WMA(S, lShort)
lWMA = WMA(S, lLong)
sWMA = sWMA[-lWMA.size:]
rawHMA = 2 * sWMA - lWMA
hma = WMA(rawHMA, lSmooth)
return hmaبه این ترتیب، تابع کامل میشود.
حال به شکل زیر تابع را فراخوانی میکنیم:
S = DF['Close'].to_numpy()
hma = HMA(S, 15)اکنون میتوان نموداری برای نمایش رفتار میانگین متحرک هال در مقابل قیمت رسم کرد:
T = np.arange(S.size)
plt.semilogy(T, S, lw=0.9, c='crimson', label='Price')
plt.semilogy(T[-hma.size:], hma, lw=0.9, c='teal', label='HMA(15)')
# plt.semilogy(T[-ema.size:], ema, lw=0.9, c='k', label='EMA(15)')
# plt.semilogy(T[-wma.size:], wma, lw=0.9, c='lime', label='WMA(15)')
plt.title('MSFT Last 1 Year Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()که در خروجی شکل زیر را خواهیم داشت.
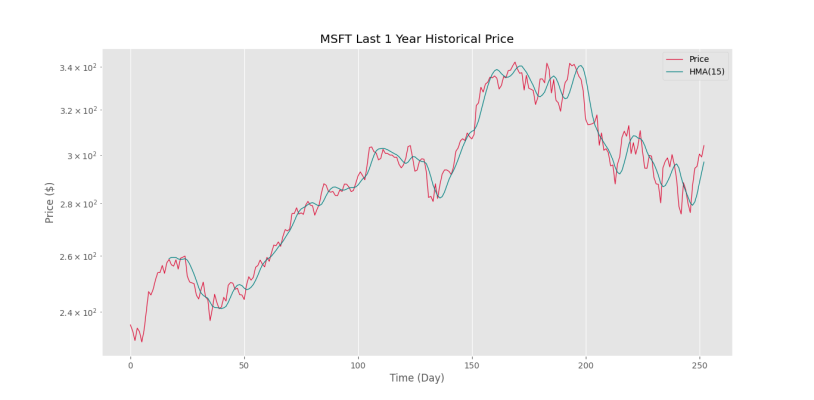
به این ترتیب، مشاهده میکنیم که رفتار بسیار مناسبی از میانگین متحرک هال ایجاد میشود. با افزایش طول پنجره از ۱۵ به ۳۰، نمودار به شکل زیر تغییر مییابد.
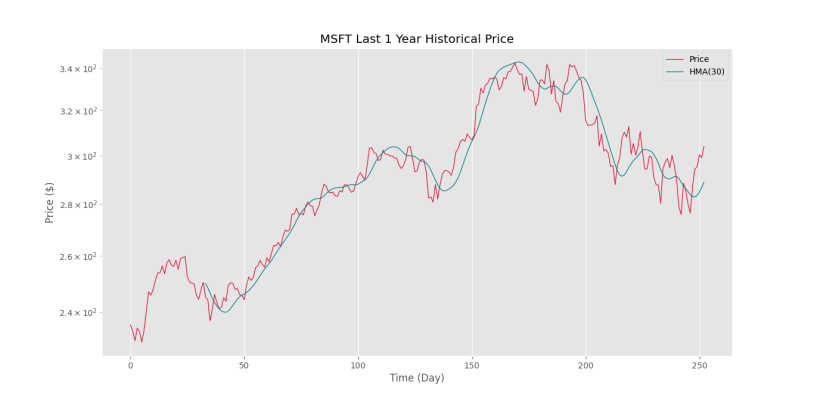
مشاهده میکنیم که با دو برابر شدن طول پنجره، همچنان تأخیر کم است. این مورد یکی از نقاط قوت میانگین متحرک هال است.
برای مقایسه رفتار این میانگین متحرک با سایرین، کد مربوط به میانگین متحرک ساده را نیز وارد کد میکنیم:
def SMA(S:np.ndarray, L:int):
nD0 = np.size(S)
nD = nD0 - L + 1
sma = np.zeros(nD)
for i in range(nD):
sma[i] = np.mean(S[i:i + L])
return smaحال برای رسم نمودار، به شکل زیر عمل میکنیم:
sma = SMA(S, 30)
wma = WMA(S, 30)
hma = HMA(S, 30)
T = np.arange(S.size)
plt.semilogy(T, S, lw=0.9, c='crimson', label='Price')
plt.semilogy(T[-sma.size:], sma, lw=0.9, c='teal', label='SMA(30)')
plt.semilogy(T[-wma.size:], wma, lw=0.9, c='k', label='WMA(30)')
plt.semilogy(T[-hma.size:], hma, lw=0.9, c='lime', label='HMA(30)')
plt.title('MSFT Last 1 Year Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()که در خروجی شکل زیر حاصل خواهد شد.
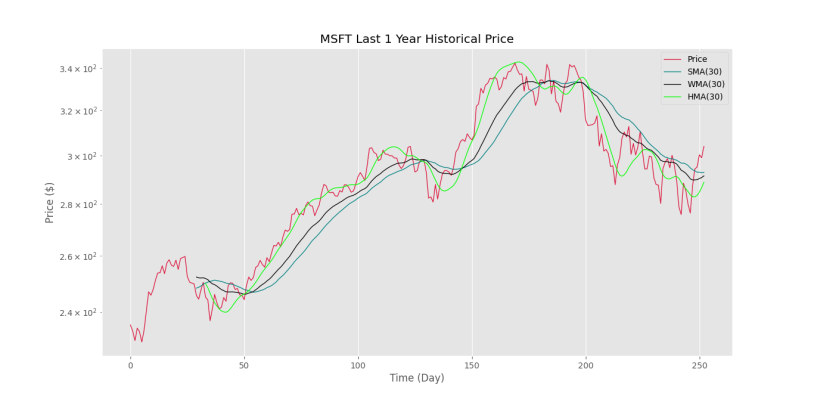
به این ترتیب، چند نکته در نمودار نمایان میشود:
- میانگین متحرک ساده دارای بیشترین تأخیر و میانگین متحرک هال دارای کمترین تأخیر است.
- میانگین متحرک هال، در هر روند، داخل شمعها حرکت میکند.
- تقاطع این سه میانگین متحرک تقریباً با هم همزمان است.
- یک بار شکست میانگین متحرک هال، نشانه خوبی از ضعیف شدن روند است که پس از آن به احتمال زیاد خنثی شدن روند و به دنبال آن تغییر روند مشاهده میشود.
- میانگین متحرک هال، مومنتوم (Momentum) قیمت را بهتر نشان میدهد.
- میانگین متحرک هال، تمایل بالایی به خطی شدن در طول روند دارد.
- علامت تغییرات میانگین متحرک هال، ارتباط بالایی با جهت روند کلی دارد.
برای بررسی مورد ۷، به شکل زیر تفاضل مقادیر میانگین متحرک هال را محاسبه میکنیم:
hma = HMA(S, 30)
dhma = hma[1:] - hma[:-1]حال میتوانیم دو نمودار رسم کنیم که در بالایی قیمت و در پایین تغییرات میانگین متحرک هال را نشان دهد:
z = np.zeros_like(dhma)
T = np.arange(S.size)
plt.subplot(2,1,1)
plt.semilogy(T, S, lw=0.8, c='teal', label='Price')
plt.title('MSFT Last 1 Year Historical Price')
plt.ylabel('Price ($)')
plt.xlim(left=-1, right=S.size)
plt.subplot(2,1,2)
plt.fill_between(T[-dhma.size:], z, dhma, where=(dhma >= z), color='lime')
plt.fill_between(T[-dhma.size:], z, dhma, where=(dhma توجه داشته باشید که به دلیل اختلاف در طول آرایه قیمت و dHMA، باید xlim تعیین شود مقدار محود X بین هر دو نمودار یکسان باشد.
پس از اجرا نمودار زیر حاصل میشود.
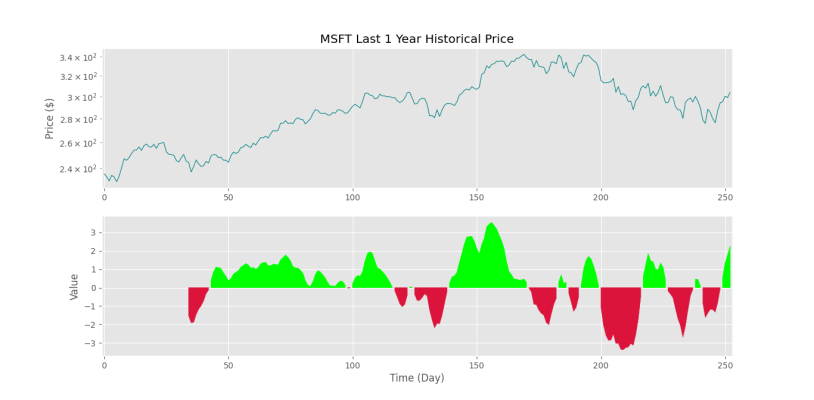
به این ترتیب مشاهده میکنیم که تمایل درونی بازار برای رشد یا ریزش، بهخوبی با تغییرات میانگین متحرک هال همبستگی دارد. به همین دلیل، در تحلیل تکنیکال (Technical Analysis) علاوه بر رسم نمودار میانگین متحرک هال، رنگ آن را نیز با توجه به علاوت تغییرات تعیین میکنند که بسیار کمککننده است.
معرفی فیلم آموزش پیاده سازی اندیکاتورهای تکنیکال با پایتون Python
اندیکاتورهای مالی از ابزارهای مهم تحلیل معاملات هستند که با کمک زبانهای برنامهنویسی میتوان محاسبات مربوط به آنها را انجام داد. در آموزش پیاده سازی اندیکاتورهای تکنیکال با پایتون Python که در ۲ ساعت و ۱۶ دقیقه تهیه و تدوین شده است، ضمن آشنایی کوتاه با ۱۰ اندیکاتور پرکاربرد، پیادهسازی گام به گام آنها در محیط زبان برنامهنویسی پایتون (Python) ارائه شده است.
- برای مشاهده آموزش پیاده سازی اندیکاتورهای تکنیکال با پایتون Python + اینجا کلیک کنید.
جمعبندی
در این مطلب، با میانگین متحرک هال آشنا شدیم، روش محاسبه و پیادهسازی آن را بررسی کردیم و در نهایت با برخی ویژگیهای آن آشنا شدیم.
برای مطالعه بیشتر، میتوان موارد زیر را بررسی کرد:
- اگر به جای استفاده از WMA در محاسبات، از EMA استفاده کنیم، نتایج چگونه خواهد بود؟
- سایر نکات گفتهشده در مورد ویژگیهای میانگین متحرک هال را بررسی کرده و به شکل نمودار نشان دهید.
- مقدار مناسب برای طول پنجره را در بازه ۱۰ روز تا ۱۰۰ روز بیابید.
- ارتباط بین علامت تغییرات SMA و EMA و WMA را با روند قیمت مقایسه کنید.
- نمودار Raw HMA را به همراه HMA رسم کنید و رفتار هر کدام را توضیح دهید.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش پیادهسازی انواع میانگین های متحرک در پایتون» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- میانگین متحرک چیست؟ + پیاده سازی Moving Average در پایتون
- پیاده سازی میانگین متحرک نمایی در پایتون — راهنمای گام به گام
- میانگین متحرک نمایی دوگانه و سه گانه در پایتون — راهنمای گام به گام
- میانگین متحرک وزن دار در پایتون — راهنمای گام به گام
- پیاده سازی میانگین متحرک هال در پایتون — راهنمای گام به گام(همین مطلب)

