میانگین متحرک وزن دار در پایتون — راهنمای گام به گام

در مطالب گذشته مجله فراردس، با میانگین متحرک ساده (SMA)، میانگین متحرک نمایی (EMA) و میانگین متحرک نمایی دوگانه و سهگانه آشنا شدیم. در این آموزش، روش پیاده سازی میانگین متحرک وزن دار در پایتون را شرح میدهیم.

میانگین متحرک وزن دار
علاوه بر روش وزندهی نمایی، میتوان وزندهی خطی را نیز استفاده کرد. به این روش، میانگین متحرک وزندار (Weighted Moving Average) یا WMA گفته میشود که بعضاً با اسم میانگین متحرک وزندار زمانی (Time Weighted Moving Average) یا TWMA نیز شناخته میشود.
در این روش نیز به دادههای اخیر وزن بیشتری داده میشود و تأخیر کمتری نسبت به میانگین متحرک ساده ایجاد میشود. وزنها، با یکدیگر یک دنباله عددی ایجاد میکنند که مجموع آنها برابر $$1$$ است. برای مثال اگر طول پنجره برابر $$3$$ باشد، میانگین متحرک وزندار به شکل زیر محاسبه میشود:
$$ W M A_{t}=sum_{i=1}^{3} w_{i} x_{t-i+1}=w_{1} x_{t}+w_{2} x_{t-1}+w_{3} x_{t-2} $$
برای وزنها میتوان روابط زیر را نوشت:
$$begin{aligned}
w_{1}-w_{2}& =w_{2}-w_{3}=d \
w_{1}+w_{2}+w_{3}&=1
end{aligned} $$
به این ترتیب، با حل روابط، مقادیر وزنها به شکل زیر محاسبه میشود:
$$ begin{aligned}
&w_{1}=frac{3}{6} \
&w_{2}=frac{2}{6} \
&w_{3}=frac{1}{6}
end{aligned} $$
به این ترتیب، قدر نسبت بین وزنها برابر $$frac 1 6 $$ بوده و مجموع وزنها نیز برابر $$1$$ است.
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
محاسبه وزنها در پایتون
وارد محیط برنامهنویسی پایتون شده و کتابخانههای مورد نیاز را فراخوانی میکنیم:
import numpy as np
import matplotlib.pyplot as pltسپس تنظیمات مربوط به نمودار را تعیین میکنیم:
plt.style.use('ggplot')حال طول بازه را تعیین میکنیم:
L = 15اکنون میتوانیم یک دنباله هندسی با قدر نسبت $$1$$ تولید کنیم:
W = np.arange(start=L, stop=0, step=-1)میدانیم که مجموع آرایه وزنها، برابر $$1$$ نخواهد بود، به همین دلیل باید تمامی وزنها را به مجموع مقادیر وزنها تقسیم کنیم:
W = W / W.sum()حال اگر مجموع مقادیر وزنها را نشان دهیم:
print(f'Sum of Weights are: {np.sum(W)}')خروجی به صورت زیر خواهد بود:
Sum of Weights are: 1.0
برای بررسی قدر نسبت بین وزنها نیز میتوان نوشت:
D = W[:-1] - W[1:]
print(f'Difference of Weights are:n{D}')که در این خروجی نیز خواهیم داشت:
Difference of Weights are: [0.00833333 0.00833333 0.00833333 0.00833333 0.00833333 0.00833333 0.00833333 0.00833333 0.00833333 0.00833333 0.00833333 0.00833333 0.00833333 0.00833333]
به این ترتیب، مشاهده میکنیم که اختلاف وزنها با هم برابر بوده و مجموعه نیز برای 1 است.
میتوان در نموداری رابطه وزنها را با یکدیگر نشان داد:
plt.bar(np.arange(L), W, width=0.3, color='lime')
plt.title(f'Weighted for L={L}')
plt.xlabel('Lag')
plt.ylabel('Weight')
plt.xticks(np.arange(L))
plt.show()و نمودار زیر حاصل میشود.
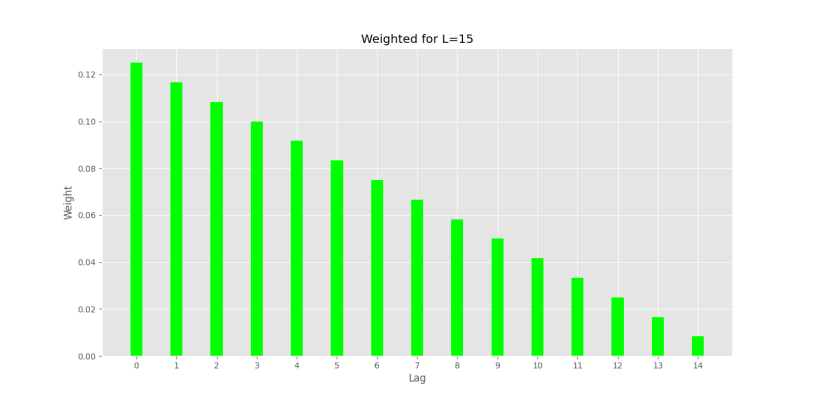
به این ترتیب، مشاهده میکنیم که آخرین روز، بیشترین وزن را دارد و در طی یک روند خطی، با دور شدن از آخرین روز، وزن داده نیز کاهش مییابد.
پیادهسازی میانگین متحرک وزن دار در پایتون
پیادهسازی میانگین متحرک وزندار در پایتون، ابتدا کتابخانههای زیر را فراخوانی میکنیم:
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as pltحال تنظیمات نمودارها را اعمال کرده و داده مورد نیاز را دریافت میکنیم:
plt.style.use('ggplot')
Ticker = yf.Ticker('AAPL')
DF = Ticker.history(interval='1d', start='2021-01-01', end='2022-01-01')در دو سطر کد فوق، نماد مربوط به شرکت Apple تعریف شده و سپس داده قیمت روزانه مربوط به یک سال از آن در قالب یک دیتافریم (Data Frame) دریافت میشود.
حال میتوانیم پنج سطر ابتدایی داده را مشاهده کنیم:
print(DF.head())که خواهیم داشت:
Open High Low Close Volume Dividends Stock Splits Date 2020-12-31 133.088923 133.744048 130.746367 131.709198 99116600 0.0 0 2021-01-04 132.533082 132.622413 125.823047 128.453461 143301900 0.0 0 2021-01-05 127.937271 130.766210 127.480664 130.041595 97664900 0.0 0 2021-01-06 126.775939 130.081327 125.445840 125.664215 155088000 0.0 0 2021-01-07 127.411211 130.657044 126.914907 129.952286 109578200 0.0 0
به این ترتیب، مشاهده میکنیم که مجموعه داده بهدرستی دریافت شده است.
حال میتوانیم مقادیر ستون Close را تبدیل به یک آرایه کرده و یک نمودار خطی (Line Plot) برای قیمت آن رسم کنیم:
S = DF['Close'].to_numpy()
plt.semilogy(S, lw=0.9, c='crimson')
plt.title('AAPL 1 Year Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.show()به این ترتیب، شکل زیر را خواهیم داشت.
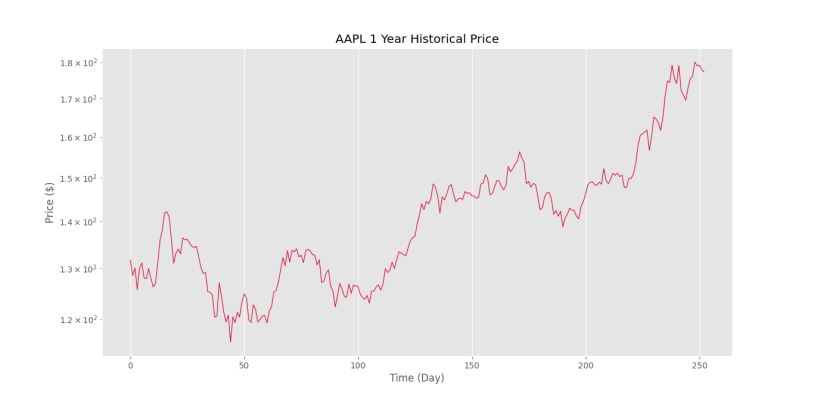
به این ترتیب نمودار قیمت حاصل شد.
حال تابعی برای محاسبه میانگین متحرک وزندار ایجاد میکنیم که در ورودی، داده سری زمانی و طول بازه میانگینگیری را دریافت میکند:
def WMA(S:np.ndarray, L:int):اکنون میتوانیم ماتریس وزن را داخل تابع محاسبه کنیم:
def WMA(S:np.ndarray, L:int):
W = np.arange(start=1, stop=L+1, step=1)
W = W / W.sum()توجه داشته باشید که آخرین روز داده، در انتهای پنجره زمانی قرار دارد، به همین دلیل، ماتریس وزن باید به صورت صعودی ایجاد شود.
حال اندازه سری ورودی و سایز سری خروجی را محاسبه میکنیم:
def WMA(S:np.ndarray, L:int):
W = np.arange(start=1, stop=L+1, step=1)
W = W / W.sum()
nD0 = S.size
nD = nD0 - L + 1حال یک آرایه خالی برای ذخیره مقدار میانگین متحرک ایجاد میکنیم:
def WMA(S:np.ndarray, L:int):
W = np.arange(start=1, stop=L+1, step=1)
W = W / W.sum()
nD0 = S.size
nD = nD0 - L + 1
wma = np.zeros(nD)حال میتوانیم یک حلقه ایجاد کرده و مقدار را برای هر روز محاسبه کنیم و در نهایت ماتریس خروجی را برگردانیم:
def WMA(S:np.ndarray, L:int):
W = np.arange(start=1, stop=L+1, step=1)
W = W / W.sum()
nD0 = S.size
nD = nD0 - L + 1
wma = np.zeros(nD)
for i in range(nD):
wma[i] = np.multiply(S[i:i + L], W).sum()
return wmaتوجه داشته باشید که تابع np.multiply اعضای دو ماتریس ورودی را نظیر به نظیر به همدیگر ضرب میکند. برای گرفتن مجموع، باید از متد sum استفاده کنیم.
حال برای استفاده از تابع پیادهسازی شده، به شکل زیر عمل میکنیم:
wma = WMA(S, 15)حال برای رسم نمودار، به شکل زیر عمل میکنیم:
T = np.arange(S.size)
plt.semilogy(T, S, lw=0.9, c='crimson', label='Price')
plt.semilogy(T[-wma.size:], wma, lw=0.9, c='teal', label='WMA(15)')
plt.title('AAPL 1 Year Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()به این ترتیب، نمودار زیر حاصل میشود.
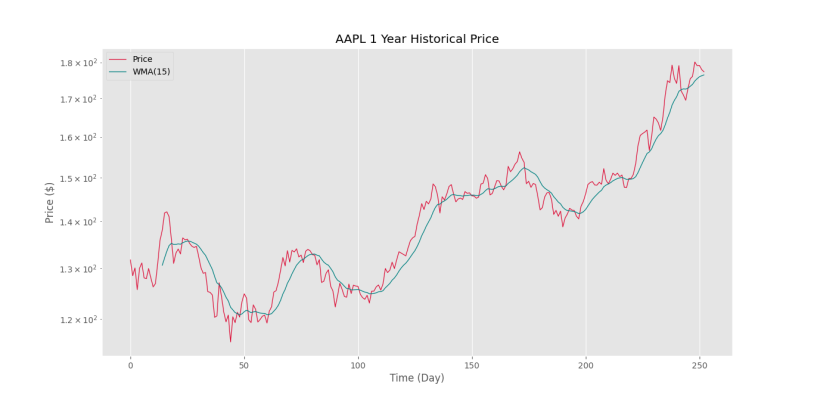
به این ترتیب، میانگین متحرک وزندار محاسبه شده، به خوبی نقش حمایت و مقاومت را ایفا میکند.
برای مقایسه رفتار میانگین متحرک ساده، نمایی و وزندار، ابتدا توابع مربوط به آنها را وارد برنامه میکنیم:
def SMA(S:np.ndarray, L:int):
nD0 = np.size(S)
nD = nD0 - L + 1
sma = np.zeros(nD)
for i in range(nD):
sma[i] = np.mean(S[i:i + L])
return sma
def EMA(S:np.ndarray, L:int, r:float=1):
a = (1 + r) / (L + r)
nD0 = S.size
nD = nD0 - L + 1
ema = np.zeros(nD)
ema[0] = np.mean(S[:L])
for i in range(1, nD):
ema[i] = a * S[i+L-1] + (1-a) * ema[i-1]
return emaحال به شکل زیر هر سه اندیکاتور را محاسبه کرده و نمودار را رسم میکنیم:
sma = SMA(S, 30)
ema = EMA(S, 30)
wma = WMA(S, 30)
T = np.arange(S.size)
plt.semilogy(T, S, lw=0.9, c='crimson', label='Price')
plt.semilogy(T[-sma.size:], sma, lw=0.9, c='teal', label='SMA(30)')
plt.semilogy(T[-ema.size:], ema, lw=0.9, c='k', label='EMA(30)')
plt.semilogy(T[-wma.size:], wma, lw=0.9, c='lime', label='WMA(30)')
plt.title('AAPL 1 Year Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()که نمودار زیر حاصل میشود.
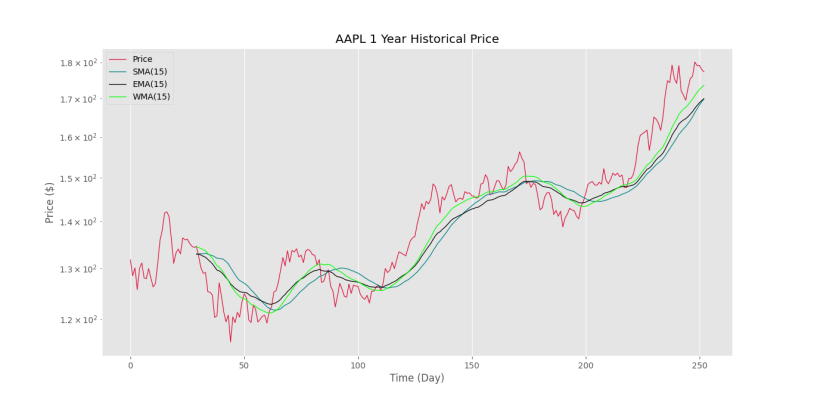
به این ترتیب مشاهده میکنیم که میانگین متحرک وزندار، رفتار نسبتاً بهتری از خود نشان میدهد.
جمعبندی
در این آموزش، میانگین متحرک وزندار را بررسی و پیادهسازی و در نهایت مزیت آن نسبت به سایر روشها که قبلاً بررسی شده بودند را مطالعه کردیم.
برای مطالعه بیشتر میتوان موارد زیر را بررسی کرد:
- تقاطع کدام دو میانگین متحرک میتواند سیگنال بهتری برای رشد یا ریزش قیمت باشد؟
- کدام میانگین متحرک با شیب بیشتری به تغییر جهت واکنش نشان میدهد؟
- از بین میانگین متحرک نمایی و میانگین متحرک وزندار، کدامیک سطوح معتبرتری را نشان میدهد؟
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش پیادهسازی انواع میانگین های متحرک در پایتون» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- میانگین متحرک چیست؟ + پیاده سازی Moving Average در پایتون
- پیاده سازی میانگین متحرک نمایی در پایتون — راهنمای گام به گام
- میانگین متحرک نمایی دوگانه و سه گانه در پایتون — راهنمای گام به گام
- میانگین متحرک وزن دار در پایتون — راهنمای گام به گام(همین مطلب)
- پیاده سازی میانگین متحرک هال در پایتون — راهنمای گام به گام

