متعادل کردن داده در پایتون — بخش دوم: تغییر مجموعه داده

پیشتر، در آموزش «متعادل کردن داده در پایتون — بخش اول: وزن دهی دسته ها» با روش وزندهی دستهها برای متعادل کردن داده در پایتون آشنا شدیم. در این آموزش، به روش دیگری برای متعادل کردن داده در پایتون میپردازیم که روش تغییر مجموعه داده نام دارد.

روشهای متعادل کردن داده
برای برقراری تعادل بین دو دسته، دو راهکار وجود دارد:
- کاهش اندازه دستههای بزرگ با Undersampling
- افزایش اندازه دستههای کوچک با Oversampling
در روش اول، تعدادی از دادههای کلاسهای بزرگتر را حذف میکنیم تا تعداد دادههای تمامی دستهها با هم برابر باشد. در این روش، اگر دستهای با تعداد دادههای خیلی کم موجود باشد، بخش بسیار بزرگی از دادهها از دست خواهد رفت.
برای مثال اگر 4 دسته با تعداد دادههای زیر داشته باشیم:
| Size | Class |
| 20 | A |
| 50 | B |
| 30 | C |
| 10 | D |
پس از انجام عملیات Undersampling به یک مجموعه داده با اندازه 40 میرسیم. این در شرایطی است که 110 داده در ابتدا موجود بود. بنابراین، یکی از نقطه ضعفهای این روش، موجود بودن دستههایی با اندازه بسیار پایینتر است.
در روش دوم، از دادههای کلاسهای کوچکتر نمونههای مشابه تولید میکنیم. برای مثال، اگر داده با ویژگیهای زیر مربوط به دسته D باشد:
$$ large x=[1.2 ;; ;-0.2 ;;; 2.3;;; -1.9] $$
با اطمینان بالایی میتوان گفت که داده زیر نیز مربوط به دسته D است:
$$ large x=[1.1 ;; ;-0.2 ;;; 2.3;;; -1.8] $$
بنابراین، میتوان از هر داده واقعی موجود در کلاس D، به تعداد زیادی داده جدید تولید کرد، به گونهای که 10 داده به 50 داده تبدیل شود.
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
متعادل کردن داده در پایتون: روش تغییر مجموعه داده
برای آشنایی با روش تغییر مجموعه داده در پایتون وارد محیط برنامهنویسی میشویم تا هر دو روش را پیادهسازی کنیم:
import numpy as np
import sklearn.datasets as dt
import matplotlib.pyplot as pltاین کتابخانهها به ترتیب برای کار روی آرایهها، استفاده از مجموعه داده IRIS و رسم نمودار مورد استفاده قرار خواهند گرفت.
ابتدا تنظیمات زیر را برای Seed و Style انجام میدهیم:
np.random.seed(0)
plt.style.use('ggplot')حال مجموعه داده IRIS را فراخوانی کرده و یک مجموعه داده نامتعادل از آن ایجاد میکنیم:
IRIS = dt.load_iris()
ind = list(range(0, 50)) + list(range(50, 70)) + list(range(100, 130))
X = IRIS.data[ind]
Y = IRIS.target[ind]
TN = IRIS.target_namesحال برای بررسی تعداد دادههای هر کلاس میتوان نوشت:
N = {tn: Y[Y == i].size for i, tn in enumerate(TN)}
print(N)که خواهیم داشت:
{'setosa': 50, 'versicolor': 20, 'virginica': 30}
به این ترتیب مشاهده میکنیم که مجموعه دادهای نامتعادل ایجاد شده است.
پیادهسازی روش Undersampling
حال میخواهیم روش Undersampling را با استفاده از یک تابع پیادهسازی کنیم. این تابع در وردی X و Y را خواهد گرفت:
def Undersample(X:np.ndarray, Y:np.ndarray):سپس نیاز است تا تمامی Labelها شناسایی شود:
def Undersample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)حال باید تعداد دادههای موجود برای هر Label شمارش شود:
def Undersample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}حال باید اندازه کوچکترین دسته تعیین شود:
def Undersample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}
nMin = min(list(N.values()))حال دو لیست خالی برای X و Yهای خروجی ایجاد میکنیم:
def Undersample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}
nMin = min(list(N.values()))
uX = []
uY = []حال باید حلقه اصلی تابع را بنویسیم و به ازای هر دسته، به صورت تصادفی دادههایی انتخاب و به لیستهای ایجاد شده اضافه کنیم:
def Undersample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}
nMin = min(list(N.values()))
uX = []
uY = []
for i in Labels:
ind = np.random.choice(N[i], nMin)
Xi = X[Y == i]
for j in Xi[ind]:
uX.append(j)
uY.append(i)
return np.array(uX), np.array(uY)به این ترتیب، به ازای هر دسته، به تعداد nMin داده انتخاب شده و index آنها در متغیر ind ذخیره میشود. سپس X دادههای مربوط به دسته i انتخاب میشود.
در حلقه دوم، دادههای انتخاب شده که درون ind ذخیره شدهاند، یک یک به لیستهای ایجاده شده اضافه میشوند. در نهایت نیز لیستهای نهایی را به آرایه تبدیل کرده و در خروجی تابع دریافت میکنیم.
برای فراخوانی تابع مینویسیم:
uX, uY = Undersample(X, Y)برای بررسی خروجی تابع میتوانیم بنویسیم:
uN = {tn: uY[uY == i].size for i, tn in enumerate(TN)}
print(f'{uX.shape = }')
print(f'{uY.shape = }')
print(f'{uN = }')که خواهیم داشت:
uX.shape = (60, 4)
uY.shape = (60,)
uN = {'setosa': 20, 'versicolor': 20, 'virginica': 20}
به این ترتیب، نتایج مورد انتظار تولید شده است و این مجموعه داده میتواند برای آموزش مدل مورد استفاده قرار گیرد.
پیادهسازی روش Oversampling
حال میخواهیم روش Oversampling را با استفاده از یک تابع پیادهسازی کنیم.
سه سطر ابتدای تابع Oversample و Undersample با هم مشابه است:
def Oversample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}در این مرحله باید بزرگترین اندازه دسته مشخص شود:
def Oversample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}
nMax = max(list(N.values()))همچنین به دو لیست برای نگهداری مقادیر ورودی و خروجی دادهها نیاز داریم:
def Oversample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}
nMax = max(list(N.values()))
uX = []
uY = []به این ترتیب، موارد گفته شده اضافه میشوند.
حال حلقه اصلی تابع را مینویسیم. به ازای هر دسته، میتوان نوشت:
def Oversample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}
nMax = max(list(N.values()))
uX = []
uY = []
for i in Labels:ابتدا دادههای موجود در دسته را بدون تغییر اضافه میکنیم:
def Oversample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}
nMax = max(list(N.values()))
uX = []
uY = []
for i in Labels:
Xi = X[Y == i]
for j in Xi:
uX.append(j)
uY.append(i)حال اختلاف اندازه دسته $$i$$ با بزرگترین دسته را محاسبه میکنیم:
def Oversample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}
nMax = max(list(N.values()))
uX = []
uY = []
for i in Labels:
Xi = X[Y == i]
for j in Xi:
uX.append(j)
uY.append(i)
nDiff = nMax - N[i]حال باید به تعداد nDiff داده جدید از روی دادههای موجود تولید کنیم. برای این کار یک حلقه ایجاد میکنیم:
def Oversample(X:np.ndarray, Y:np.ndarray):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}
nMax = max(list(N.values()))
uX = []
uY = []
for i in Labels:
Xi = X[Y == i]
for j in Xi:
uX.append(j)
uY.append(i)
nDiff = nMax - N[i]
for j in range(nDiff):حال باید داده اصلی را انتخاب کنیم:
for j in range(nDiff):
x = Xi[np.random.randint(N[i])]حال باید به صورت تصادفی روی برخی از ویژگیهای x تغییراتی تصادفی اعمال کنیم. برای تعیین تعداد ویژگیهایی که باید تغییر کنند، یک ورودی دیگر برای تابع با نام nMutation تعریف میکنیم که یک عدد صحیح خواهد بود:
def Oversample(X:np.ndarray, Y:np.ndarray, nMutation:int):حال میتوانیم ویژگیهایی را برای تغییر انتخاب کنیم:
for j in range(nDiff):
x = Xi[np.random.randint(N[i])]
f = np.random.choice(X.shape[1], nMutation)حال میتوانیم ویژگیهای انتخاب شده در f را تغییر دهیم:
for j in range(nDiff):
x = Xi[np.random.randint(N[i])]
f = np.random.choice(X.shape[1], nMutation)
for k in f:
x[k] *= np.random.uniform(1-0.1, 1+0.1)به این ترتیب، تغییراتی تصادفی در x ایجاد میشود.
توجه داشته باشید که برای ایجاد اندکی نویز در مقدار اولیه ویژگی، میتوان روشهای مختلف را استفاده کرد:
- مقداردهی تصادفی براساس توزیع آماری دادهها
- ضرب در یک عددی در بازه $$ [1-e,1+e] $$
- افزودن یک عدد در بازه $$[-e,+e]$$
حال x نهایی را به همراه دسته به لیستهای ایجاد شده اضافه میکنیم:
for j in range(nDiff):
x = Xi[np.random.randint(N[i])]
f = np.random.choice(X.shape[1], nMutation)
for k in f:
x[k] *= np.random.uniform(1-0.1, 1+0.1)
uX.append(x)
uY.append(i)به این ترتیب، تمامی موارد گفته شده اعمال میشود و در نهایت نیاز است تا دو لیست ایجاد شده تبدیل به آرایه شده و خروجی داده شوند:
def Oversample(X:np.ndarray, Y:np.ndarray, nMutation:int):
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}
nMax = max(list(N.values()))
uX = []
uY = []
for i in Labels:
Xi = X[Y == i]
for j in Xi:
uX.append(j)
uY.append(i)
nDiff = nMax - N[i]
for j in range(nDiff):
x = Xi[np.random.randint(N[i])]
f = np.random.choice(X.shape[1], nMutation)
for k in f:
x[k] *= np.random.uniform(1-0.1, 1+0.1)
uX.append(x)
uY.append(i)
return np.array(uX), np.array(uY)تا به اینجا تابع کامل است. میتوان در برخی موارد نیز بهبودهایی داده و تابع را به شکل زیر در آورد:
def Oversample(X:np.ndarray, Y:np.ndarray, nMutation:int, e:float=0.1):
nX = X.shape[1]
Labels = np.unique(Y)
N = {i: Y[Y == i].size for i in Labels}
nMax = max(list(N.values()))
uX = []
uY = []
for i in Labels:
Xi = X[Y == i]
for j in Xi:
uX.append(j)
uY.append(i)
nDiff = nMax - N[i]
for j in range(nDiff):
x = Xi[np.random.randint(N[i])]
f = np.random.choice(nX, nMutation)
for k in f:
x[k] *= np.random.uniform(1-e, 1+e)
uX.append(x)
uY.append(i)
return np.array(uX), np.array(uY)
به این ترتیب، رفتار تابع بیشتر قابل تنظیم بوده و در برخی موارد بهینهتر عمل میکند.
حال از تابع خروجی گرفته و خروجیها را بررسی میکنیم:
oX, oY = Oversample(X, Y, 2)
oN = {tn: oY[oY == i].size for i, tn in enumerate(TN)}
print(f'{oX.shape = }')
print(f'{oY.shape = }')
print(f'{oN = }')که خواهیم داشت:
oX.shape = (150, 4)
oY.shape = (150,)
oN = {'setosa': 50, 'versicolor': 50, 'virginica': 50}
بنابراین با 100 داده نامتعادل، به 150 داده متعادل رسیدیم.
حال برای بررسی کیفیت دادههای تولید شده، آنها را با دادههای واقعی مقایسه میکنیم:
plt.subplot(2, 2, 1)
plt.scatter(IRIS.data[:, 0], IRIS.data[:, 1], c=IRIS.target, s=13)
plt.title('Main Data')
plt.xlabel('X1')
plt.ylabel('X2')
plt.xlim(4, 8)
plt.ylim(1.9, 4.5)
plt.subplot(2, 2, 2)
plt.scatter(oX[:, 0], oX[:, 1], c=oY, s=13)
plt.title('Oversampled Data')
plt.xlabel('X1')
plt.xlim(4, 8)
plt.ylim(1.9, 4.5)
plt.subplot(2, 2, 3)
plt.scatter(IRIS.data[:, 2], IRIS.data[:, 3], c=IRIS.target, s=13)
plt.xlabel('X3')
plt.ylabel('X4')
plt.xlim(0.5, 7)
plt.ylim(0, 2.7)
plt.subplot(2, 2, 4)
plt.scatter(oX[:, 2], oX[:, 3], c=oY, s=13)
plt.xlabel('X3')
plt.xlim(0.5, 7)
plt.ylim(0, 2.7)
plt.show()که در خروجی نمودار زیر حاصل میشود.
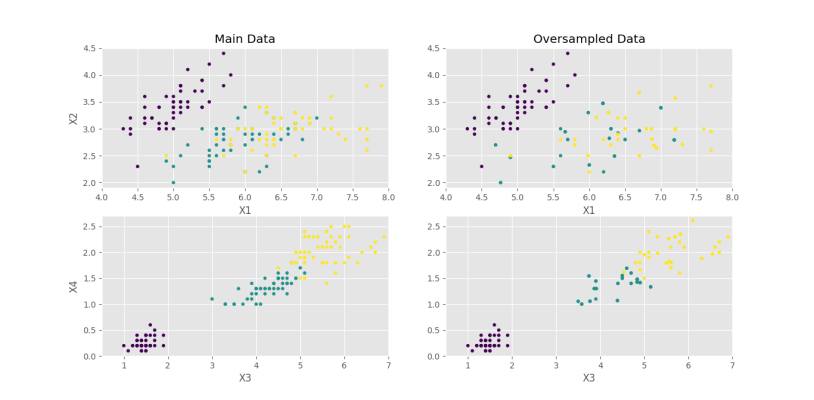
به این ترتیب مشاهده میکنیم که برای X1 و X2 نتایج متوسطی ایجاد شده است، اما برای X3 و X4 مرزهای اصلی رعایت شده است.
اگر مقدار $$e$$ را از 0٫1 به 0٫2 افزایش دهیم، شکل زیر را خواهیم داشت.
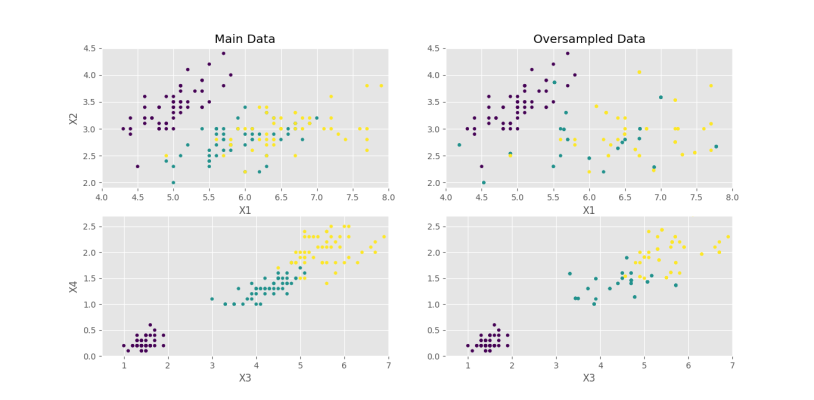
به این ترتیب، مشاهده میکنیم دادههای با فواصل بیشتر از مرکز دسته ایجاد شدهاند که به اشتباه وارد محدوده دستههای دیگر شدهاند. بنابراین، افزایش بیش از حد e میتواند دادههایی نادرست ایجاد کند. کم بودن مقدار e نیز باعث تولید دادههایی بسیار نزدیک به دادههای اصلی میشود که عملاً باعث تکرار دادههای قبلی خواهد شد.
اگر تعداد nMutation را از 2 به 4 برسانیم با e=0٫1 به نمودار زیر میرسیم.
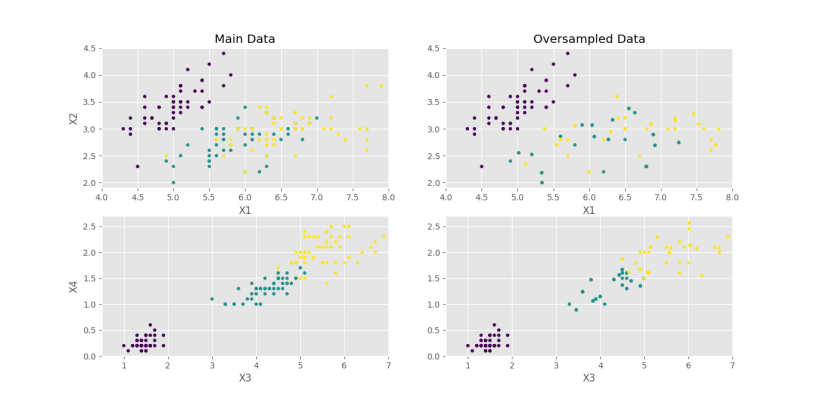
که با توجه به حالت nMutation=2 و e=0.1، تفاوتهای زیر حاصل شده است:
- به طور کلی، دادههای متنوعتری حاصل شده است.
- دادهها به مرکز دستهها بیشتر همگرا شدهاند.
- پراکندگی دادهها زیاد شده است.
بنابراین، هم مقدار e و هم مقدار nMutation مهم بوده و باید با دقت تعیین شوند.
برای بررسیهای بیشتر، میتوان این کارها را انجام داد: روند انتخاب دادهها در روش Undersampling را بهبود داد، روش اضافه کردن نویز به دادهها در روش Oversampling را تغییر داد، nMax در روش Oversampling را %80 بزرگترین دسته در نظر گرفت و ترکیبی از دو روش گفته شده را به کار برد.
جمعبندی
در این آموزش، با روشهای متعادل کردن دادهها آشنا شدیم. همچنین، تغییر مجموعه داده در پایتون را برای متعادل کردن دادهها با دو روش Undersampling و Oversampling شرح دادیم.
همچنین، روش اول یعنی روش وزندهی دستهها را میتوانید در این لینک مطالعه کنید.

