ساخت ربات معامله گر رمزارز با لگاریتم تغییرات قیمت — پیاده سازی در پایتون | تم آف

در مطالب گذشته، به کاربرد میانگین متحرک ساده و اندیکاتور استوکستیک در ایجاد و آموزش ربات‌های معامله‌گر پرداختیم. در این مطلب قصد داریم یک مدل خودهمبسته (Autoregressive) ایجاد کنیم که با استفاده از لگاریتم نسبت قیمت در L روز گذشته، سیگنال مربوط به هر روز را محاسبه کند و با توجه به آن معامله کند.

لگاریتم تغییرات قیمت

لگاریتم نسبت قیمت را می‌توانیم به شکل زیر تعریف می‌کنیم:

$$L C_{t}=log left(frac{text { Close }_{t}}{text { open }_{t}}right)$$

با توجه به اینکه قصد داریم یک مدل خودهمبسته ایجاد کنیم، با اضافه کردن اپراتور تأخیر (Lag Operator)، لگاریتم نسبت قیمت مربوط به تأخیر $$l$$ در زمان $$t$$ به شکل زیر قابل محاسبه خواهد بود:

$$ L C_{t, l}=log left(frac{C l o s e_{t-l}}{O p e n_{t-l}}right)$$

حال می‌توانیم یک مدل خودهمبسته خطی تعریف کنیم:

$$ S_{t}=sum_{l=0}^{L-1} W_{l} times L C_{t, l}=sum_{l=0}^{L-1} W_{l} times log left(frac{text { Close }_{t-l}}{text{Open }_{t-l}}right) $$

به این ترتیب سیگنال در زمان $$t$$ ترکیبی خطی از لگاریتم نسبت قیمت در $$L$$ دوره گذشته خواهد بود.

تعیین حد آستانه

برای جلوگیری از انجام معاملات اشتباه، یک حد آستانه (Threshold) تعریف می‌کنیم که همواره عددی مثبت است. با استفاده از حد آستانه، سیگنال نهایی را به شکل زیر محاسبه می‌کنیم:

$$ F S_{t}= begin{cases}0 & left|S_{t}right|

به این ترتیب، سیگنال‌های با شدت کم، به $$0$$ تنظیم می‌شوند و مانع از انجام معاملات اشتباه می‌شود. مقدار حد آستانه نیز باید بهینه‌سازی شود، به همین دلیل، آن را نیز در آرایه (Array) پارامترها در نظر می‌گیریم.

اگر در یک نمودار سیگنال نهایی را در مقابل سیگنال اولیه رسم کنیم، شکل زیر را خواهیم داشت.

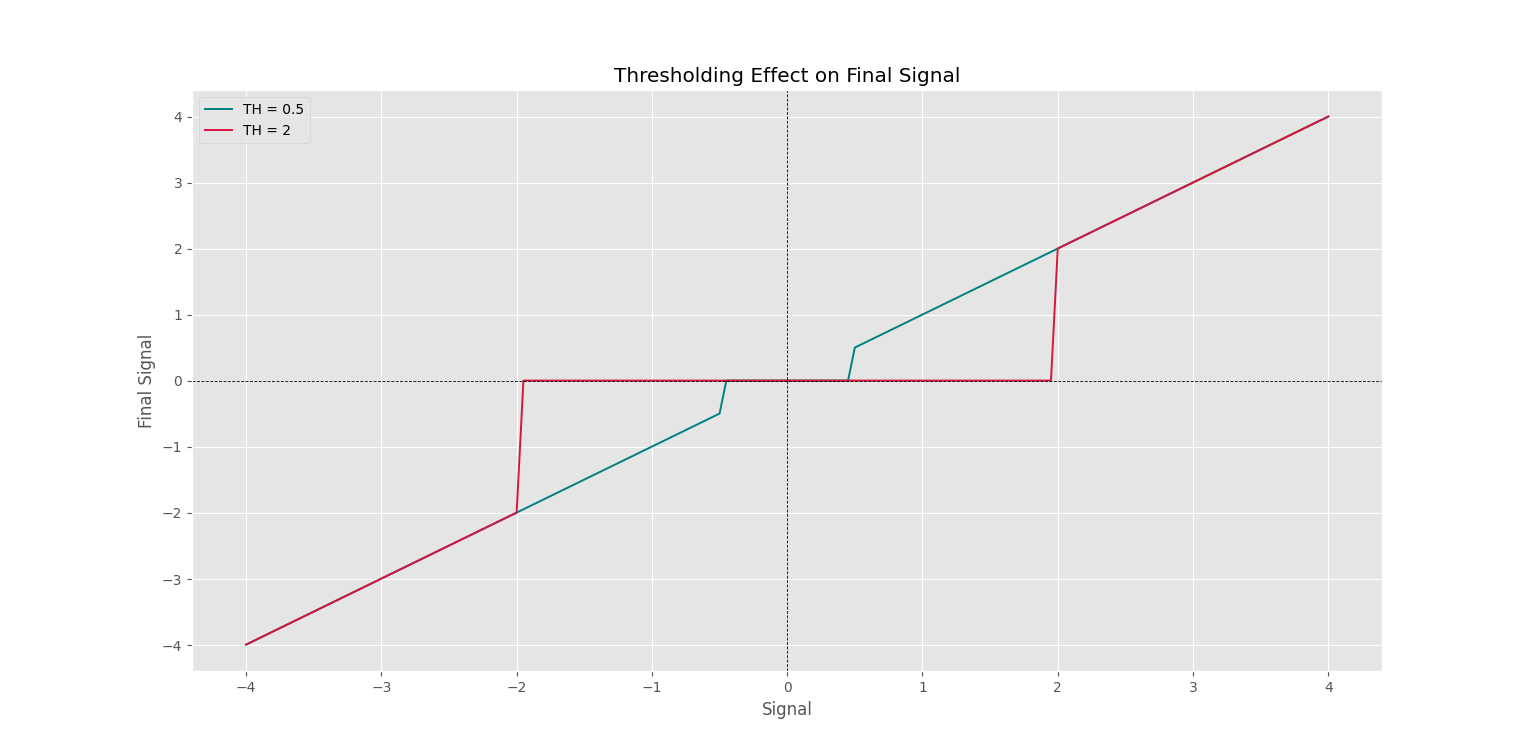
به این ترتیب، می‌توان مشاهده کرد که در بازه مقدار سیگنال نهایی برابر با صفر است و در خارج از بازه، به سیگنال ورودی واکنش نشان می‌دهد.

نظم‌دهی به ربات

با توجه به اینکه ممکن است تغییرات قیمت در برخی روزها، بدون تأثیر در سیگنال باشند، اضافه شدن آن‌ها به مدل‌سازی سیگنال، باعث بیش‌برازش (Overfitting) ربات خواهد شد. به همین دلیل، از یک جمله نظم‌دهی (Regularization Term) نیز برای جلوگیری از این اتفاق استفاده می‌کنیم. جمله نظم‌دهی را از درجه دوم در نظر گرفته و به شکل زیر تعریف می‌کنیم:

$$G(W)=lambda sum_{l=0}^{L-1} W_{l}^{2}=lambda|W|_{2}^{2} $$

حال می‌توانیم تابع هزینه را به شکل زیر ایجاد کنیم:

$$L(W, T H)=-R(W, T H)+G(W) $$

تابع $$R$$ نشان‌دهنده بازده ربات است که با شبیه‌سازی معاملات در طول زمان به دست می‌آید. به این ترتیب هم سود ربات بیشینه می‌شود، هم از انجام معاملات اشتباه جلوگیری می‌شود و هم به ربات نظم‌دهی می‌شود تا بیش‌برازش رخ ندهد.

پیاده‌سازی ربات

حال برای پیاده‌سازی ربات، وارد محیط برنامه‌نویسی می‌شویم و کتابخانه‌های مورد نیاز را فراخوانی می‌کنیم:

این کتابخانه‌ها به ترتیب برای موارد زیر استفاده خواهند شد:

import numpy as np
import pandas as pd
import pyswarm as ps
import pandas_datareader as pdt
import matplotlib.pyplot as plt

1. محاسبات برداری و ایجاد آرایه
2. کار با دیتافریم‌ها
3. بهینه‌سازی ربات
4. دریافت داده به صورت برخط (Online)
5. رسم نمودار

حال کلاس مربوط به ربات را ایجاد می‌کنیم:

class arLCbot:

متد سازنده را تعریف می‌کنیم و در ورودی مقدار $$L$$ (که نشان‌دهنده پنجره زمانی نگاه به گذشته است) و نسبت اندازه مجموعه داده آموزش (Train Dataset) به مجموعه داده کل را دریافت می‌کنیم:

    def __init__(self, L:int, sTrain:float=0.6):

حال پارامترهای ورودی را در شیء ذخیره و دو لیست مربوط به Log بازده، خطا و مقدار نظم‌دهی در طول فرآیند آموزش را ایجاد می‌کنیم:

    def __init__(self, L:int, sTrain:float=0.6):
        self.L = L
        self.sTrain = sTrain
        self.TrainLogReturn = []
        self.TrainLogLoss = []
        self.TrainLogRegularization = []

پیاده‌سازی متد دریافت داده

حال می‌توانیم متد دیگری برای دریافت داده مربوط به نماد مورد نظر ایجاد کنیم:

    def GetData(self, Ticker:str, Start:str, End:str):

ورودی‌های تابع را در شیء ذخیره می‌کنیم:

    def GetData(self, Ticker:str, Start:str, End:str):
        self.Ticker = Ticker
        self.Start = Start
        self.End = End

سپس دیتافریم مربوط به قیمت نماد را دریافت می‌کنیم و در شیء ذخیره می‌کنیم:

    def GetData(self, Ticker:str, Start:str, End:str):
        self.Ticker = Ticker
        self.Start = Start
        self.End = End
        self.DF = pdt.DataReader(Ticker,
                                 data_source='yahoo',
                                 start=Start,
                                 end=End)

حال ستون‌های اضافی موجود را نیز حذف می‌کنیم:

    def GetData(self, Ticker:str, Start:str, End:str):
        self.Ticker = Ticker
        self.Start = Start
        self.End = End
        self.DF = pdt.DataReader(Ticker,
                                 data_source='yahoo',
                                 start=Start,
                                 end=End)
        self.DF.drop(labels=['Volume', 'Adj Close'],
                     axis=1,
                     inplace=True)

به این ترتیب، مجموعه داده خام دریافت و ذخیره خواهد شد.

پیاده‌سازی متد پردازش داده

حال برای پردازش داده، یک متد دیگری تعریف می‌کنیم که هیچ ورودی‌ای به جز شیء ندارد:

    def ProcessData(self):

در اولین قدم، لگاریتم نسبت قیمت را محاسبه می‌کنیم و آن را به عنوان یک ستون به دیتافریم اضافه می‌کنیم:

    def ProcessData(self):
        self.DF['LC'] = np.log(self.DF['Close'] / self.DF['Open'])

حال می‌توانیم با استفاده از یک حلقه، برای تمامی تأخیرها از $$0$$ تا $$L-1$$ ستون مورد نظر را ایجاد کنیم. برای این فرآیند از متد shift استفاده می‌کنیم:

    def ProcessData(self):
        self.DF['LC'] = np.log(self.DF['Close'] / self.DF['Open'])
        for i in range(self.L):
            self.DF[f'LC(t-{i})'] = self.DF['LC'].shift(i)

حال ستون مربوط به اولین فرصت خرید را نیز اضافه می‌کنیم که قیمت Open روز بعد را نشان می‌دهد:

    def ProcessData(self):
        self.DF['LC'] = np.log(self.DF['Close'] / self.DF['Open'])
        for i in range(self.L):
            self.DF[f'LC(t-{i})'] = self.DF['LC'].shift(i)
        self.DF['FP'] = self.DF['Open'].shift(-1)

با توجه به ایجاد مقدار NaN یا Not a Number در برخی سطرها، آن‌ها را حذف می‌کنیم. سپس اندازه مجموعه داده حاصل را محاسبه، و اندازه مجموعه داده آموزش را محاسبی می‌کنیم. در نهایت، دو مجموعه داده آموزش و آزمایش را جدا و در شیء ذخیره می‌کنیم:

    def ProcessData(self):
        self.DF['LC'] = np.log(self.DF['Close'] / self.DF['Open'])
        for i in range(self.L):
            self.DF[f'LC(t-{i})'] = self.DF['LC'].shift(i)
        self.DF['FP'] = self.DF['Open'].shift(-1)
        self.DF.dropna(inplace=True)
        self.nD = len(self.DF)
        self.nDtr = round(self.sTrain * self.nD)
        self.nDte = self.nD - self.nDtr
        self.trDF = self.DF.iloc[:self.nDtr, :]
        self.teDF = self.DF.iloc[self.nDtr:, :]

به این ترتیب، در این متد، داده خام پردازش، ستون‌های مورد نیاز اضافه، سپس عملیات پاکسازی و تقسیم داده صورت می‌گیرد.

پیاده‌سازی متد شبیه‌سازی معامله

حال متد مربوط شبیه‌سازی انجام معاملات را ایجاد می‌کنیم و در ورودی مقدار حد آستانه، ماتریس وزن‌ها (ضرایب تأخیرها) و دیتافریم را دریافت می‌کنیم:

    def Trade(self, TH:float, W:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)

در مرحله بعد، سه آرایه برای ذخیره پول، سهم و ارزش پرتفوی در طول زمان ایجاد می‌کنیم:

    def Trade(self, TH:float, W:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)

حال دو دیکشنری نیز برای ذخیره سابقه معاملات خرید و فروش به طور جداگانه ایجاد می‌کنیم:

    def Trade(self, TH:float, W:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}

به این ترتیب، تمامی متغیرها برای ذخیره تاریخچه ربات کامل خواهد بود. حال باید سیگنال را در طول زمان محاسبه کنیم. برای این منظور، باید ماتریس وزن هر روز را در ماتریس تأخیر در طول روزهای مختلف (ماتریس X) ضرب کنیم. بنابراین ماتریس مربوط به تأخیرهای مختلف در طول مجموعه داده را از دیتافریم جدا می‌کنیم:

    def Trade(self, TH:float, W:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        X = DF.iloc[:, -self.L - 1:-1].to_numpy()

توجه داشته باشید که ستون آخر دیتافریم مربوط به اولین فرصت خرید است و $$L$$ ستون قبل آن مربوط به تأخیرهای مورد نظر است که برای محاسبه سیگنال مورد نیاز هستند. حال ضرب ماتریسی بین وزن‌ها ($$W$$) و ماتریس $$X$$ را انجام می‌دهیم و سیگنال اولیه حاصل می‌شود:

    def Trade(self, P:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        X = DF.iloc[:, -self.L - 1:-1].to_numpy()
        Signals = np.dot(X, P)

حال باید به کمک حد آستانه، سیگنال نهایی را محاسبه کنیم، که خواهیم داشت:

    def Trade(self, TH:float, W:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        X = DF.iloc[:, -self.L - 1:-1].to_numpy()
        Signals = np.dot(X, W)
        Signals[np.abs(Signals) 

به این ترتیب، سیگنال حاصل ترکیبی خطی از لگاریتم نسبت قیمت در L روز گذشته خواهد بود که برای هر روز قابل محاسبه است و مقادیر با شدت کم، به عدد صفر گرد شده‌اند. حال سرمایه اولیه و سهام اولیه را تعیین می‌کنیم و حلقه مربوط به معامله را ایجاد می‌کنیم:

    def Trade(self, TH:float, W:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        X = DF.iloc[:, -self.L - 1:-1].to_numpy()
        Signals = np.dot(X, W)
        Signals[np.abs(Signals) 

حال اولین فرصت خرید و سیگنال روز مربوطه را استخراج می‌کنیم:

    def Trade(self, TH:float, W:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        X = DF.iloc[:, -self.L - 1:-1].to_numpy()
        Signals = np.dot(X, W)
        Signals[np.abs(Signals) 

حال شروط مربوط به انجام معامله را نوشته، تبدیلات بین پول و سهام را انجام و در نهایت معامله انجام‌شده را در تاریخچه ذخیره می‌کنیم:

    def Trade(self, TH:float, W:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        X = DF.iloc[:, -self.L - 1:-1].to_numpy()
        Signals = np.dot(X, W)
        Signals[np.abs(Signals)  0 and share == 0:
                share = money / fp
                money = 0
                Buys['Time'].append(i)
                Buys['Price'].append(fp)
            elif signal  0:
                money = share * fp
                share = 0
                Sells['Time'].append(i)
                Sells['Price'].append(fp)

در انتهای روز معاملاتی نیز پول، سهم و ارزش پرتفوی را محاسبه و ذخیره می‌کنیم:

    def Trade(self, TH:float, W:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        X = DF.iloc[:, -self.L - 1:-1].to_numpy()
        Signals = np.dot(X, W)
        Signals[np.abs(Signals)  0 and share == 0:
                share = money / fp
                money = 0
                Buys['Time'].append(i)
                Buys['Price'].append(fp)
            elif signal  0:
                money = share * fp
                share = 0
                Sells['Time'].append(i)
                Sells['Price'].append(fp)
            Moneys[i] = money
            Shares[i] = share
            Values[i] = money + share * fp

به این ترتیب، محاسبات مربوط به هر روز انجام خواهد شد. در انتها نیاز داریم تا میانگین بازده روزانه و نرخ بُرد (Win Rate) را نیز محاسبه کنیم و خروجی‌های مورد نیاز را برگردانیم. به این منظور خواهیم داشت:

    def Trade(self, TH:float, W:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        X = DF.iloc[:, -self.L - 1:-1].to_numpy()
        Signals = np.dot(X, W)
        Signals[np.abs(Signals)  0 and share == 0:
                share = money / fp
                money = 0
                Buys['Time'].append(i)
                Buys['Price'].append(fp)
            elif signal  0:
                money = share * fp
                share = 0
                Sells['Time'].append(i)
                Sells['Price'].append(fp)
            Moneys[i] = money
            Shares[i] = share
            Values[i] = money + share * fp
        Return = 100 * ((Values[-1] / Values[0])**(1 / (nD - 1)) - 1)
        wr = WR(Buys, Sells)
        return Moneys, Shares, Values, Signals, Buys, Sells, wr, Return

تابع مربوط به محاسبه نرخ برد را نیز به شکل زیر تعریف می‌کنیم:

def WR(Buys:dict, Sells:dict):
    nT = 0 # Count of Total Trader
    nW = 0 # Count of Wins
    for b, s in zip(Buys['Price'], Sells['Price']):
        nT += 1
        if s > b:
            nW += 1
    if nT != 0:
        return 100 * nW / nT
    return 0

به این ترتیب، متد مربوط به شبیه‌سازی معامله نیز تکمیل می‌شود.

پیاده‌سازی متد تابع هزینه

حال متد مربوط به تابع هزینه (Loss Function) را ایجاد می‌کنیم و در ورودی پارامترها، دیتافریم و مقدار لاندا (λ) که برای نظم‌دهی ربات هست را دریافت می‌کنیم:

    def Loss(self, P:np.ndarray, DF:pd.core.frame.DataFrame, Lambda:float=8e-2):

حال، در اولین اقدام، مقدار حد آستانه و آرایه وزن‌ها را از پارامترها استخراج می‌کنیم. به طور قراردادی، اولین عضو پارامترها را حد آستانه در نظر می‌گیریم:

    def Loss(self, P:np.ndarray, DF:pd.core.frame.DataFrame, Lambda:float=8e-2):
        TH = P[0]
        W = P[1:]

سپس متد Trade را فراخوانی می‌کنیم و از بین تمامی خروجی‌ها، آخرین مورد که مربوط به میانگین بازده روزانه است را با نام $$r$$ تعریف می‌کنیم:

    def Loss(self, P:np.ndarray, DF:pd.core.frame.DataFrame, Lambda:float=8e-2):
        TH = P[0]
        W = P[1:]
        R = self.Trade(TH, W, DF)[-1]

حال مقدار جمله نظم‌دهی را محاسبه و سپس مقدار هزینه را محاسبه می‌کنیم:

    def Loss(self, P:np.ndarray, DF:pd.core.frame.DataFrame, Lambda:float=8e-2):
        TH = P[0]
        W = P[1:]
        R = self.Trade(TH, W, DF)[-1]
        G = Lambda * np.power(W, 2).sum()
        L = -R + G

اکنون مقدار بازده، هزینه و مقدار نظم‌دهی را در لیست‌های مربوط ذخیره می‌کنیم. در نهایت نیز، مقدار هزینه را برمی‌گردانیم:

    def Loss(self, P:np.ndarray, DF:pd.core.frame.DataFrame, Lambda:float=8e-2):
        TH = P[0]
        W = P[1:]
        R = self.Trade(TH, W, DF)[-1]
        G = Lambda * np.power(W, 2).sum()
        L = -R + G
        self.TrainLogReturn.append(R)
        self.TrainLogLoss.append(L)
        self.TrainLogRegularization.append(G)
        return L

به این ترتیب، تابع هزینه برای بهینه‌سازی پارامترها آماده است.

پیاده‌سازی متد بهینه‌ساز

در این مرحله، نیاز داریم تا یک متد نیز برای انجام فرایند آموزش ربات ایجاد کنیم. این متد از الگوریتم بهینه‌سازی ازدحام ذرات (Particle Swarm Optimization یا PSO) استفاده خواهد، به همین دلیل، در ورودی تعداد ذرات و بیشترین تعداد مراحل را دریافت می‌کند:

    def Train(self, SS:int, MI:int):

حال، حد پایین (Lower Bound) و حد بالا (Upper Bound) وزن‌ها را از $$-1$$ تا $$+1$$ تعیین می‌کنیم:

    def Train(self, SS:int, MI:int):
        lb = -1 * np.ones(self.L + 1)
        ub = +1 * np.ones(self.L + 1)

با توجه به اینکه حد آستانه همواره مثبت است و نباید مقادیر خیلی بزرگی به خود بگیرد، آن را نیز بین $$0.005$$ و $$0.15$$ محدود می‌کنیم:

    def Train(self, SS:int, MI:int):
        lb = -1 * np.ones(self.L + 1)
        ub = +1 * np.ones(self.L + 1)
        lb[0] = 0.005
        ub[0] = 0.15

حال تابع pso از کتابخانه pyswarm را بر روی تابع هزینه اعمال می‌کنیم و سایر ورودی‌ها را نیز تعریف می‌کنیم:

    def Train(self, SS:int, MI:int):
        lb = -1 * np.ones(self.L + 1)
        ub = +1 * np.ones(self.L + 1)
        lb[0] = 0.005
        ub[0] = 0.15
        self.P, self.BestLoss = ps.pso(self.Loss,
                                       lb,
                                       ub,
                                       args=(self.trDF, ),
                                       swarmsize=SS,
                                       maxiter=MI)

این تابع، در خروجی به ترتیب بهترین جواب و بهترین مقدار تابع هزینه را برمی‌گرداند که به ترتیب در self.P و self.BestLoss ذخیره می‌کنیم.

مقدار حد آستانه و آرایه وزن‌ها را نیز استخراج و در شی ذخیره می‌کنیم:

    def Train(self, SS:int, MI:int):
        lb = -1 * np.ones(self.L + 1)
        ub = +1 * np.ones(self.L + 1)
        lb[0] = 0.005
        ub[0] = 0.15
        self.P, self.BestLoss = ps.pso(self.Loss,
                                       lb,
                                       ub,
                                       args=(self.trDF, ),
                                       swarmsize=SS,
                                       maxiter=MI)
        self.TH = self.P[0]
        self.W = self.P[1:]

حال می‌توانیم میانگین بازده روزانه را نیز محاسبه کنیم:

    def Train(self, SS:int, MI:int):
        lb = -1 * np.ones(self.L + 1)
        ub = +1 * np.ones(self.L + 1)
        lb[0] = 0.005
        ub[0] = 0.15
        self.P, self.BestLoss = ps.pso(self.Loss,
                                       lb,
                                       ub,
                                       args=(self.trDF, ),
                                       swarmsize=SS,
                                       maxiter=MI)
        self.TH = self.P[0]
        self.W = self.P[1:]
        self.BestReturn = self.Trade(self.TH,
                                     self.W,
                                     self.trDF)[-1]

به این ترتیب، کلیه موارد در شرایط بهینه محاسبه می‌شود. حال نیاز داریم تا نتایج را نمایش دهیم:

    def Train(self, SS:int, MI:int):
        lb = -1 * np.ones(self.L + 1)
        ub = +1 * np.ones(self.L + 1)
        lb[0] = 0.005
        ub[0] = 0.15
        self.P, self.BestLoss = ps.pso(self.Loss,
                                       lb,
                                       ub,
                                       args=(self.trDF, ),
                                       swarmsize=SS,
                                       maxiter=MI)
        self.TH = self.P[0]
        self.W = self.P[1:]
        self.BestReturn = self.Trade(self.TH,
                                     self.W,
                                     self.trDF)[-1]
        print('_' * 60)
        print('Optimization Result:')
        print(f'tTH:        {round(self.TH, 4)}')
        for i in range(self.L):
            print(f'tW(Lag={i}): {round(self.P[i + 1], 4)}')
        print(f'tReturn:    {round(self.BestReturn, 4)} %')
        print('_' * 60)

به این ترتیب، مقدار حد آستانه، وزن هر روز و بازده روزانه حاصل نمایش داده خواهد شد.

پیاده‌سازی متد رسم نمودار وزن‌ها

حال برای مصورسازی (Visualization) وزن‌ها متد زیر را تعریف می‌کنیم تا مقدار وزن هر کدام از تأخیرها با شکل بصری قابل نمایش باشد:

    def PlotWeights(self):
        T = np.arange(start=0, stop=self.L, step=1)
        plt.bar(T,
                self.W,
                width=0.4,
                color='crimson')
        plt.axhline(lw=1, c='k')
        plt.title('Weight of Lags')
        plt.xlabel('Lag')
        plt.ylabel('Weight')
        plt.show()

توجه داشته باشید که اولین وزن به ستون مربوط به لگاریتم نسبت قیمت در روز فعلی ضرب می‌شود. به همین دلیل، ایندکس (Index) نشان‌دهنده تأخیر نیز می‌شود.

پیاده‌سازی متد رسم عملکرد ربات در طول آموزش

با توجه به اینکه در طول آموزش مدل، بازده، خطا و مقدار نظم‌دهی را ذخیره می‌کنیم، در این بخش می‌توانیم سه نمودار رسم کنیم:

    def PlotTrainLog(self):
        plt.plot(self.TrainLogReturn,
                 lw=0.8,
                 c='teal',
                 label='Return')
        plt.plot(self.TrainLogLoss,
                 lw=0.8,
                 c='crimson',
                 label='Loss')
        plt.plot(self.TrainLogRegularization,
                 lw=0.8,
                 c='lime',
                 label='Regularization')
        plt.title('Bot Return, Loss & Regularization Over Training Iterations')
        plt.xlabel('Function Evaluation')
        plt.ylabel('Value')
        plt.legend()
        plt.show()

پیاده‌سازی متد رسم نمودار قیمت و ارزش پرتفوی در طول زمان

این متد یک ورودی برای تعیین داده مورد نظر دریافت می‌کند و براساس آن نمودار را رسم می‌کند:

    def PlotValue(self, Data:str):
        if Data == 'Train':
            DF = self.trDF
        elif Data == 'Test':
            DF = self.teDF
        O = self.Trade(self.TH, self.W, DF)
        Values, bReturn = O[2], O[7]
        plt.subplot(1, 2, 1)
        hReturn = 100 * ((DF['Close'][-1] / DF['Close'][0])**(1 / (len(DF) - 1)) - 1)
        T = np.arange(start=0, stop=Values.size, step=1)
        hMeanValue = DF['Close'][0] * (1 + hReturn / 100)**T
        plt.plot(DF.index,
                 DF['Close'],
                 lw=0.8,
                 c='crimson',
                 label='Close')
        plt.plot(DF.index,
                 hMeanValue,
                 ls='--',
                 lw=1,
                 c='k',
                 label=f'Mean Values (ADR: {round(hReturn, 4)} %)')
        plt.title(f'Price Over Time ({Data})')
        plt.xlabel('Time (Day)')
        plt.ylabel('Price ($)')
        plt.yscale('log')
        plt.legend()
        plt.subplot(1, 2, 2)
        bMeanValue = (1 + bReturn / 100)**T
        plt.plot(DF.index,
                 Values,
                 lw=0.8,
                 c='crimson',
                 label='Real Values')
        plt.plot(DF.index,
                 bMeanValue,
                 ls='--',
                 lw=1,
                 c='k',
                 label=f'Mean Values (ADR: {round(bReturn, 4)} %)')
        plt.title(f'Value Over Time ({Data})')
        plt.xlabel('Time (Day)')
        plt.ylabel('Value')
        plt.yscale('log')
        plt.legend()
        plt.show()

توجه داشته باشید که میانگین بازده روزانه نماد به شکل زیر آخرین قیمت را براساس اولین قیمت و فاصله زمانی توصیف می‌کند:

$$ text { Close }_{T}=text { Close }_{1} timesleft(1+frac{A D R}{100}right)^{T-1} $$

با حل رابطه، می‌توان گفت:

$$ A D R=100 timesleft(sqrt[T-1]{frac{operatorname{Close}_{T}}{operatorname{Close}_{1}}}-1right) $$

به همین دلیل، برای محاسبه میانگین بازده روزانه نماد در حالت Hold به شکل زیر می‌نویسیم:

hReturn = 100 * ((DF['Close'][-1] / DF['Close'][0])**(1 / (len(DF) - 1)) - 1)

پیاده‌سازی متد رسم نمودار سیگنال و خرید/فروش روی قیمت

این متد نیز مانند متد قبلی روی مجموعه آموزش و آزمایش قابل فراخوانی هست، به همین دلیل یک ورودی خواهد داشت:

    def PlotSignal(self, Data:str):
        if Data == 'Train':
            DF = self.trDF
        elif Data == 'Test':
            DF = self.teDF
        O = self.Trade(self.TH, self.W, DF)
        Signals, Buys, Sells = O[3], O[4], O[5]
        plt.subplot(3, 1, (1, 2))
        plt.plot(DF.index,
                 DF['Close'].to_numpy(),
                 lw=0.7,
                 c='k',
                 label='Close')
        plt.scatter(DF.index[Buys['Time']],
                    Buys['Price'],
                    s=24,
                    c='lime',
                    marker='o',
                    label='Buy')
        plt.scatter(DF.index[Sells['Time']],
                    Sells['Price'],
                    s=24,
                    c='crimson',
                    marker='o',
                    label='Sell')
        plt.title(f'Price Over Time ({Data})')
        plt.ylabel('Price ($)')
        plt.yscale('log')
        plt.tight_layout()
        plt.legend()
        plt.subplot(3, 1, 3)
        Z = np.zeros_like(Signals)
        plt.plot(DF.index,
                 Signals,
                 lw=0.5,
                 c='k')
        plt.fill_between(DF.index,
                         Signals,
                         Z,
                         where=(Signals > Z),
                         color='lime',
                         alpha=0.9,
                         label='Buy Signal')
        plt.fill_between(DF.index,
                         Signals,
                         Z,
                         where=(Signals 

به این ترتیب، تمامی متدهای مورد نیاز برای کلاس پیاده‌سازی می‌شود.

حال برای استفاده از کلاس نوشته‌شده، ابتدا تنظیمات زیر را اعمال می‌کنیم:

np.random.seed(0)
plt.style.use('ggplot')

حال می‌توانیم ربات را ایجاد کرده و مقدار $$L$$ را برابر $$10$$ قرار دهیم. به این ترتیب، ربات از لگاریتم نسبت قیمت در $$10$$ روز اخیر برای تصمیم‌گیری استفاده خواهد کرد:

Trader = arLCbot(10)

اکنون، داده مورد نظر را دریافت می‌کنیم:

Trader.GetData('BTC-USD', '2018-01-01', '2022-05-01')

به این ترتیب، حدود $$1600$$ روز داده خام خواهیم داشت.

حال می‌توانیم مجموعه داده را پردازش و آن را تقسیم کنیم:

Trader.ProcessData()

در نهایت نیز تابع مربوط به آموزش ربات را فراخوانی می‌کنیم:

Trader.Train(SS=40, MI=15)

به این ترتیب، فرایند آموزش ربات به اتمام می‌رسد و نتایج زیر ظاهر می‌شود:

Optimization Result:
        TH:        0.0486
        W(Lag=0): -0.0569
        W(Lag=1):  0.0669
        W(Lag=2):  0.194
        W(Lag=3): -0.0351
        W(Lag=4):  0.4303
        W(Lag=5):  0.4932
        W(Lag=6): -0.3226
        W(Lag=7):  0.2929
        W(Lag=8): -0.0237
        W(Lag=9):  0.2188
        Return:    0.1887 %

مشاهده می‌کنیم که بهترین مقدار برای حد آستانه $$0.0486$$ تعیین می‌شود. به این ترتیب، سیگنال‌های بین $$-0.0486$$ و $$+0.0486$$ برای گرفتن هیچ موقعیتی استفاده نخواهد شد.

شدیدترین ارتباط سیگنال امروز نیز با $$5$$ روز قبل نشان داده می‌شود.

برای مجموعه داده آموزش نیز میانگین بازده روزانه $$0.1887$$ درصد به دست می‌آید.

حال می‌توانیم نمودار وزن‌ها را نیز به شکل زیر رسم کنیم:

Trader.PlotWeights()

که در نتیجه این دستور، نمودار زیر حاصل می‌شود.

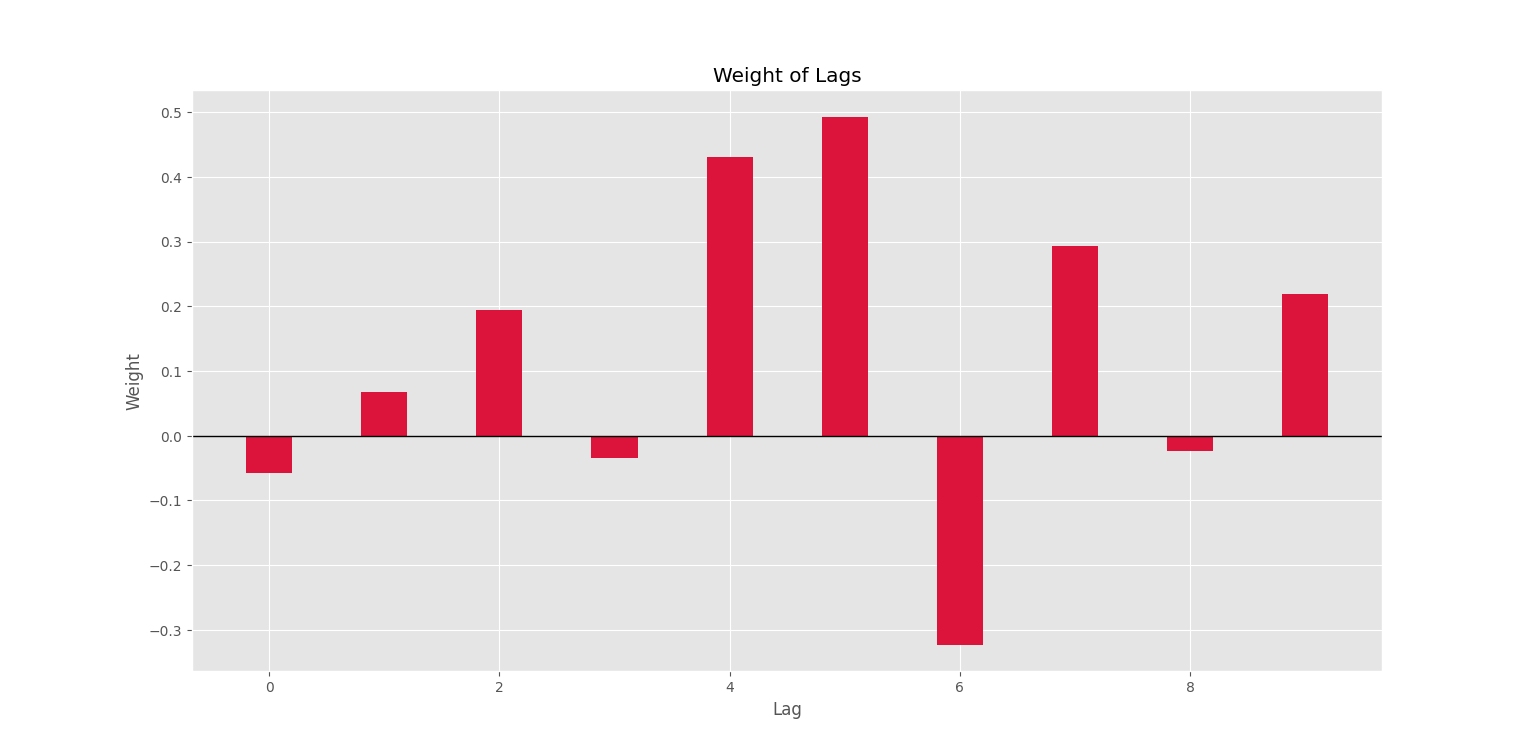
حال می‌توانیم نمودار مربوط به عملکرد ربات در طول آموزش را نیز رسم کنیم:

Trader.PlotTrainLog()

که در این صورت، نمودار زیر حاصل خواهد شد.

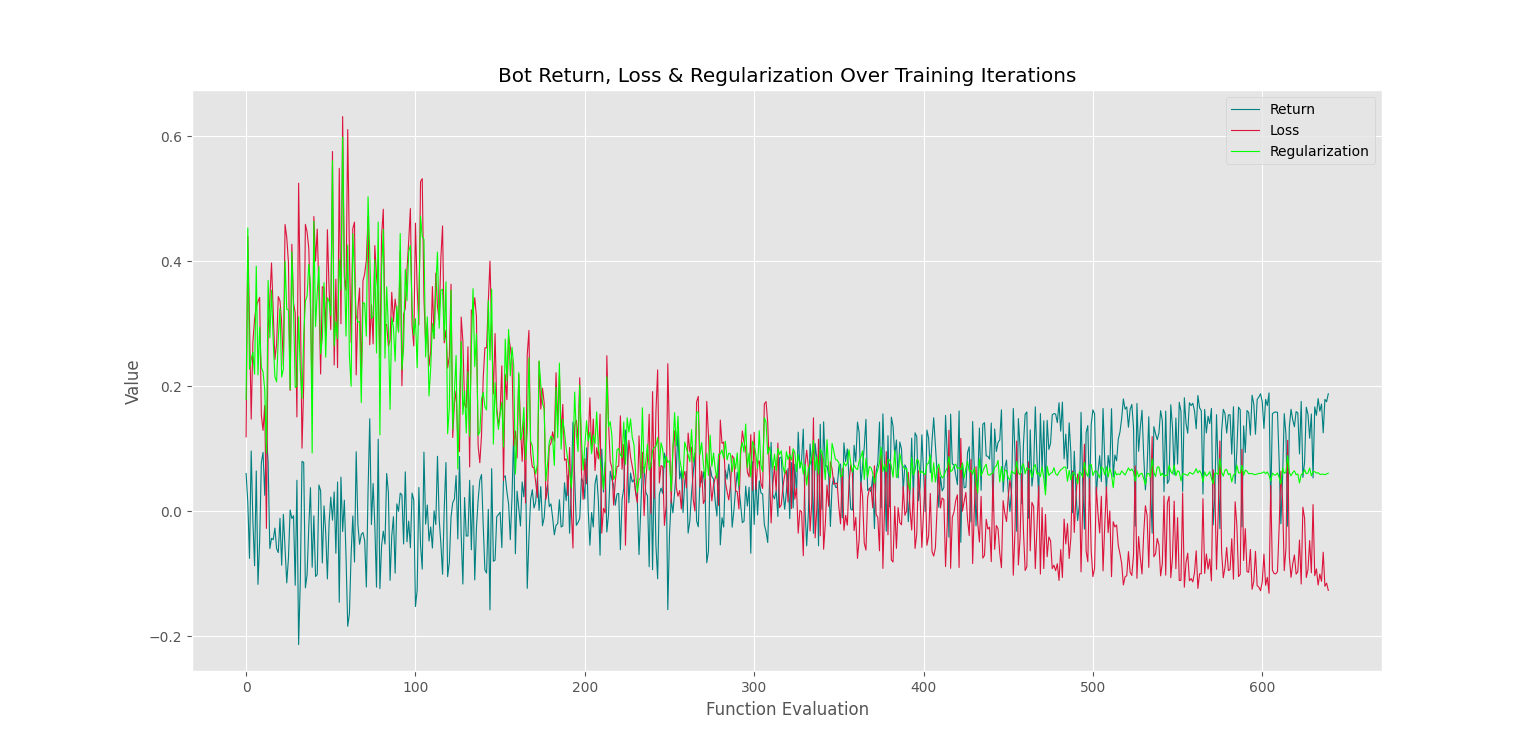
به این ترتیب، مشاهده می‌کنیم که همزمان با کاهش خطا و مقدار نظم‌دهی، بازده ربات نیز افزایش می‌یابد. توجه داشته باشید که اختلاف دو نمودار Return و Regularization برابر با نمودار Loss است.

حال می‌توانیم نمودار مربوط به بازده نماد و بازده ربات را در کنار هم رسم کنیم:

Trader.PlotValue('Train')

که نمودار زیر حاصل می‌شود.

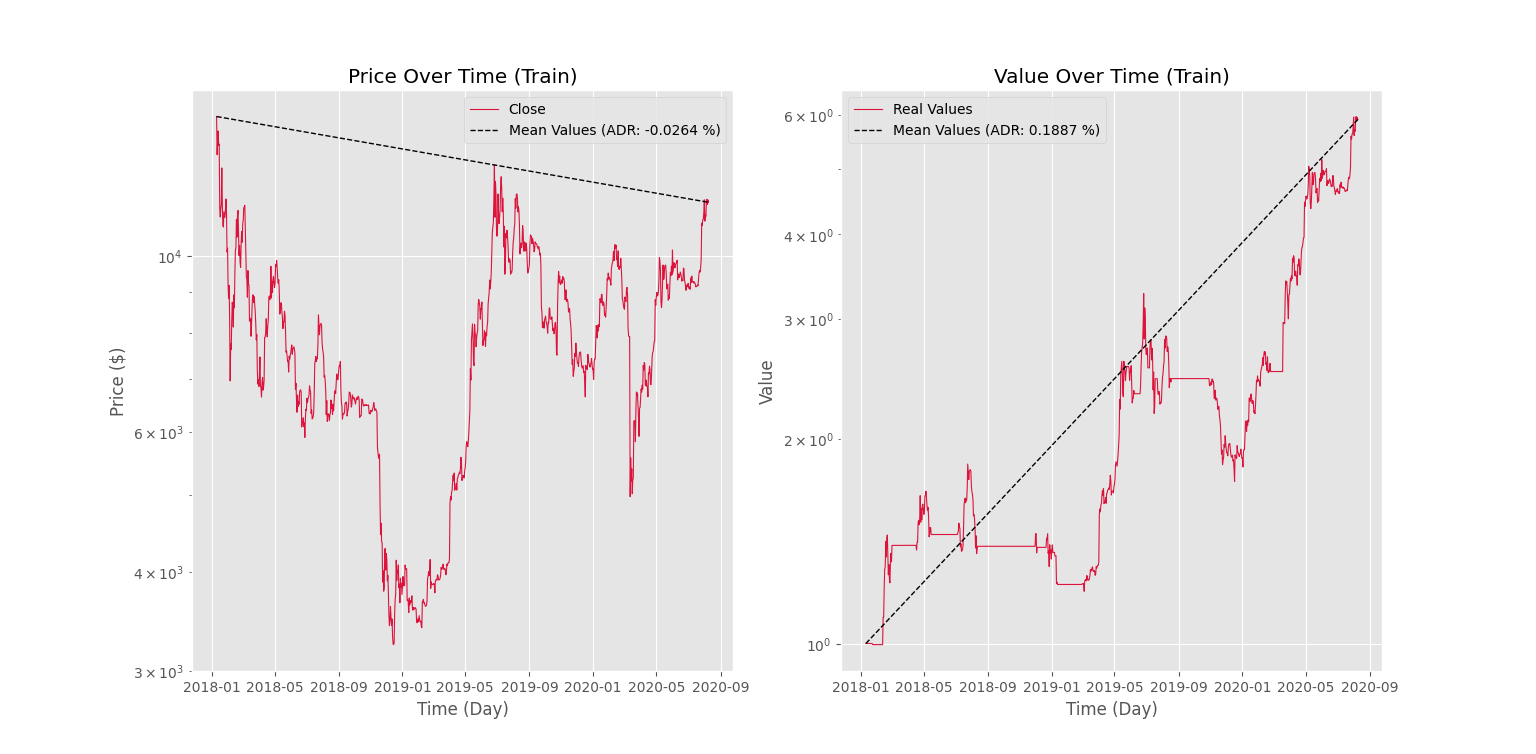
به این ترتیب، مشاهده می‌کنیم که با وجود روند و بازده منفی در خود نماد، ربات توانسته به سود روزانه $$0.1887$$ درصد برسد که بسیار مناسب است.

حال می‌توانیم نمودار سیگنال و نقاط خرید و فروش را نیز رسم کنیم:

Trader.PlotSignal('Train')

که در این مورد نیز شکل زیر را خواهیم داشت.

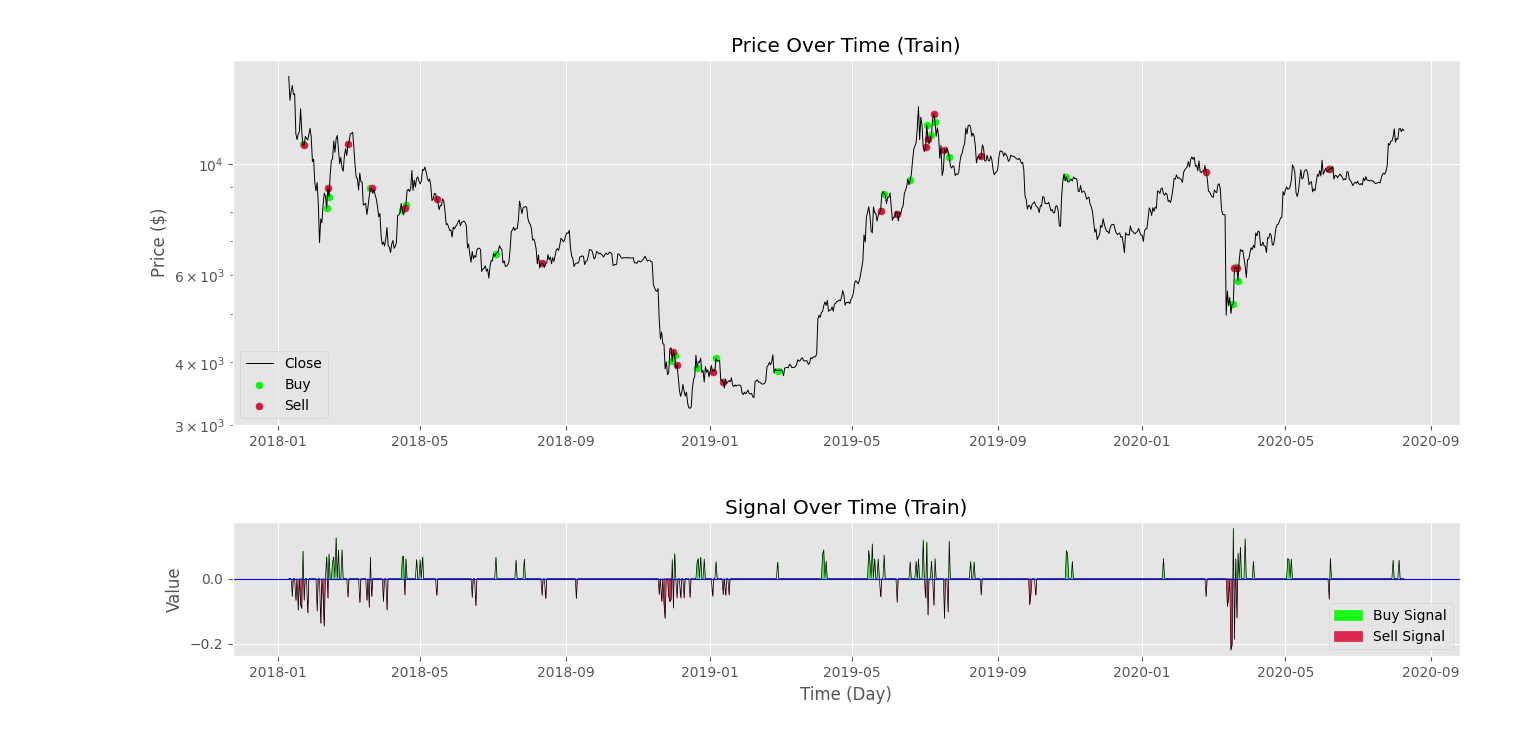
به این ترتیب، مشاهده می‌کنیم که در اغلب روزها مقدار سیگنال صفر است که به دلیل استفاده از حد آستانه است. به این ترتیب۷ تعداد کم شده است و در مقابل اعتبار آن‌ها افزایش یافته است.

می‌توانیم این دو نمودار را برای مجموعه داده آزمایش نیز تکرار کنیم، که در این صورت شکل‌های زیر را خواهیم داشت.

شکل اول به‌صورت زیر است.

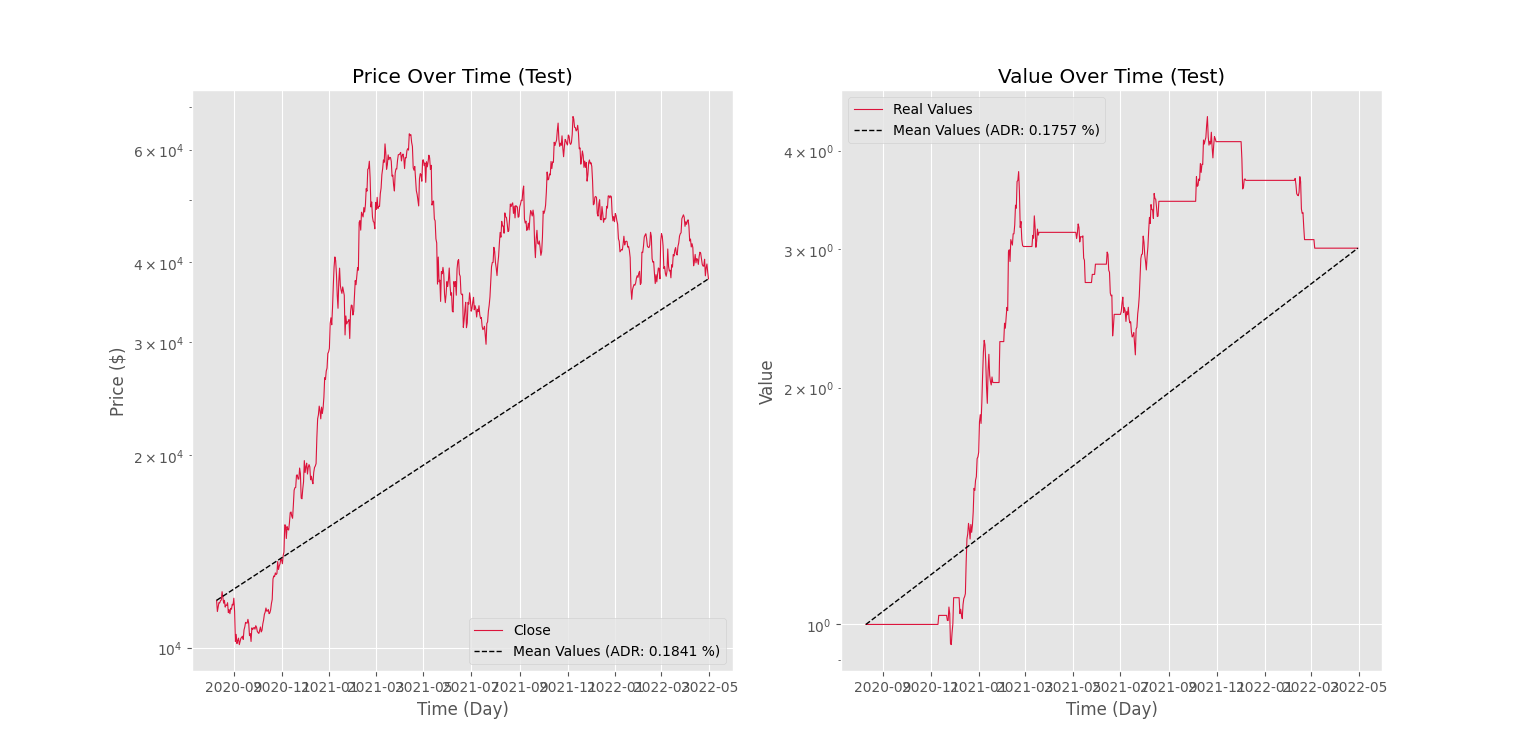
شکل دوم نیز در ادامه آورده شده است.

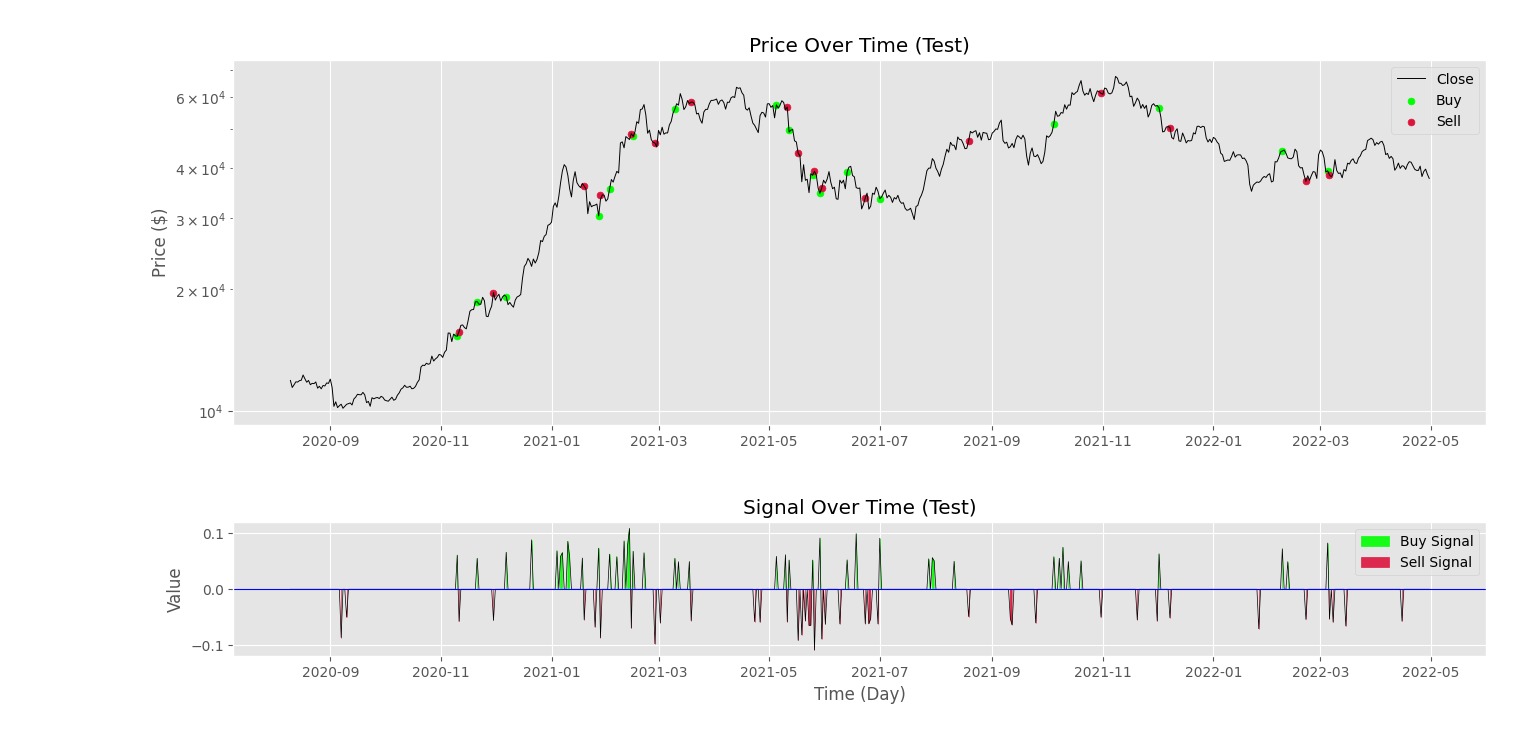
به این ترتیب، در نمودار اول مشاهده می‌کنیم که نماد از یک روند صعودی برخوردار بوده که به میانگین سود روزانه $$0.1841$$ درصد رسیده است که عدد نسبتاً بزرگی است. در مقابل، ربات نیز در بازه متناظر به میانگین سود $$0.1757$$ درصد رسیده است که مقدار نزدیکی است. در نمودار دوم می‌توان با بررسی دقیق‌تر به این نتیجه رسید که غالب سود ربات، در روندهای صعودی قوی دریافت شده است. سایر معاملات انجام‌شده در مواقعی بوده‌اند که بازار دارای روند قدرتمندی نبوده و ربات دچار ضعف در عملکرد شده است. به این دلیل، استفاده از یک مدل خودهمبسته براساس تاریخچه لگاریتم نسبت قیمت، در کنار مزایا، این ضعف را نیز دارد.

محاسبه نرخ بُرد

برای محاسبه نرخ بُرد، ابتدا متد Trade را روی هر دو مجموعه داده آموزش و آزمایش اجرا می‌کنیم:

trWR = Trader.Trade(Trader.TH,
                    Trader.W,
                    Trader.trDF)[-2]
teWR = Trader.Trade(Trader.TH,
                    Trader.W,
                    Trader.teDF)[-2]

توجه داشته باشید که متد Trade در خروجی $$8$$ متغیر برمی‌گرداند که هفتمین متغیر مربوط به نرخ بُرد است.

حال هر دو عدد حاصل را نمایش می‌دهیم:

print(f'Train Win Rate: {round(trWR, 2)} %')
print(f'Test Win Rate:  {round(teWR, 2)} %')

که خواهیم داشت:

Train Win Rate: 59.09 %
Test Win Rate:  58.82 %

به این ترتیب، مشاهده می‌کنیم که غالب معاملات سودده بوده‌اند و عملکرد روی مجموعه داده آزمایش، به عملکرد بر روی مجموعه داده آزمایش نزدیک است، بنابراین، می‌توان تعمیم‌پذیری (Generalizability) مدل را تأیید کرد.

جمع‌بندی

به این ترتیب، ربات مورد نظر را به کمک برنامه‌نویسی شی‌ءگرا (Object Oriented Programmingیا OOP) پیاده‌سازی کردیم و نتایج را تحلیل کردیم. برای مطالعه بیشتر، می‌توان موارد زیر را بررسی کرد:

1. اگر به جای لگاریتم نسبت قیمت، از تغییرات قیمت نسبی استفاده کنیم، نتایج به چه شکلی تغییر خواهد کرد؟
2. اگر مقدار λ برابر با صفر تنظیم شود، نتایج به چه شکلی خواهد بود؟
3. چگونه می‌توان این ربات را بهبود داد تا بتواند روندها را بهتر شناسایی کند؟
4. اگر در رابطه درنظر‌گرفته‌شده برای سیگنال، علاوه بر ضرایب مربوط به لگاریتم نسبت قیمت در روزهای گذشته، یک مقدار ثابت نیز به عبارت اضافه کنیم تا نقش عرض از مبدأ (Intercept) یا بایاس (Bias) را داشته باشد، نتایج به چه شکلی تغییر خواهد کرد؟ آیا تعمیم‌پذیری مدل تغییر خواهد کرد؟
5. با تقسیم مجموعه داده اولیه به 3 بخش، یک مجموعه داده ارزیابی نیز ایجاد کنید و در طول آموزش بازده ربات را برای این مجموعه داده نیز محاسبه کنید. این نمودار چه شباهتی به منحنی یادگیری (Learning Curve) دارد؟ از این نمودار چه اطلاعاتی می‌توان استخراج کرد؟