رگرسیون خطی در یادگیری ماشین — از صفر تا صد + کد

«رگرسیون خطی» (Linear Regression) اولین الگوریتم «یادگیری ماشین» (Machine Learning) برای «علم داده» (Data Science) به حساب میآید. رگرسیون خطی در یادگیری ماشین، یک مدل «یادگیری نظارتی» (Supervised Learning) محسوب میشود که در آن، هدفِ مدل پیدا کردن «بهترین خط برازش» (Best Fit Line) بین متغیرهای مستقل و وابسته است. به عبارت دیگر، این مدل بین متغیرهای مستقل و وابسته رابطهای خطی به وجود میآورد. در این مطلب به رگرسیون خطی در یادگیری ماشین طور جامع توضیح داده شده است و موارد مرتبط با آن نیز مورد بررسی قرار گرفتهاند.

رگرسیون خطی در یادگیری ماشین چیست ؟
رگرسیون خطی یکی از سادهترین و محبوبترین الگوریتمهای یادگیری ماشین به حساب میآید. این مدل، روشی آماری است و برای تجزیه و تحلیل پیشبینی استفاده میشود. رگرسیون خطی برای متغیرهای پیوسته، واقعی و عددی از جمله میزان فروش، حقوق، سن افراد، قیمت محصولات و سایر موارد مورد استفاده قرار میگیرد.
رگرسیون خطی در یادگیری ماشین رابطه خطی بین متغیری وابسته مانند Y و یک یا چند متغیر مستقل مثل X را نشان میدهد، از این رو به آن رگرسیون خطی گفته میشود. به عبارت دیگر، از آنجایی که رگرسیون خطی نشان دهنده رابطه خطی است، چگونگی تغییر مقدار متغیر وابسته را با توجه به مقدار متغیر مستقل پیدا میکند. مدل رگرسیون خطی، یک خط مستقیم شیبدار و رابطه بین متغیرها را نشان میدهد. نمودار زیر برای نشان دادن مدل رگرسیون خطی ارائه شده است.
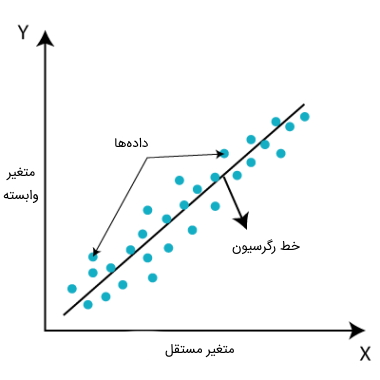
معادله ریاضی رگرسیون خطی به صورت زیر نوشته میشود:
$$y = a_0 + a_1 + ε$$
وظیفه هر کدام از متغیرهای معادله فوق در ادامه شرح داده شده است:
- Y: متغیر وابسته یا همان متغیر هدف را نشان میدهد.
- X: متغیر مستقل یا همان متغیر پیشبینی را مشخص میکند.
- $$a_0 $$: نقطهای که تابع محور Y را قطع میکند (به واسطه آن درجه بیشتری از آزادی عمل ارائه میشود).
- $$a_1 $$: ضریب رگرسیون خطی (ضریب مقیاس برای هر مقدار ورودی را نشان میدهد).
- ε: خطای تصادفی را مشخص میکند.
مقدار متغیرهای X و Y مجموعه دادههای «آموزشی» (Train) را برای مدل رگرسیون خطی در یادگیری ماشین نشان میدهند.
انواع رگرسیون خطی در یادگیری ماشین
دو نوع الگوریتم رگرسیون خطی در ماشین لرنینگ وجود دارد که در ادامه فهرست شدهاند:
- «رگرسیون خطی ساده» (Simple Linear Regression): زمانی به یک الگوریتم رگرسیون خطی ساده گفته میشود که برای پیشبینی مقدار متغیر عددی وابسته از یک متغیر مستقل واحد استفاده شود.
- «رگرسیون خطی چندگانه» (Multiple Linear regression): اگر برای پیشبینی مقدار متغیر وابسته عددی بیش از یک متغیر مستقل استفاده شود، به این مدل، رگرسیون خطی چندگانه گفته میگویند.
در ادامه این نوشتار هر کدام از انواع الگوریتمهای رگرسیون خطی در یادگیری ماشین شرح داده شدهاند.
رگرسیون خطی ساده در یادگیری ماشین چیست ؟
خطی که رابطه بین متغیرهای وابسته و مستقل را نشان میدهد، «خط رگرسیون» (Regression Line) نامیده میشود.
به طور کلی خط رگرسیون میتواند دو نوع ارتباط زیر را نشان دهد:
- «ارتباط خطی مثبت» (Positive Linear Relationship): اگر متغیر وابسته محور Y افزایش پیدا کند و متغیر مستقل روی محور X افزایش داشته باشد، به این ارتباط خطی به اصطلاح ارتباط رگرسیون خطی مثبت گفته میشود. در ادامه نموداری با این نوع از ارتباط نمایش داده شده است.
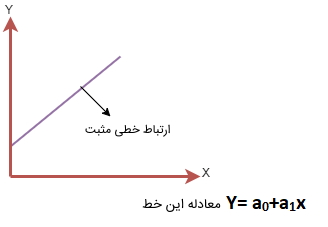
- «ارتباط خطی منفی» (Negative Linear Relationship): اگر متغیرهای وابسته روی محور Y کاهش پیدا کنند و متغیرهای مستقل روی محور X افزایش داشته باشند، رابطه رگرسیون خطی منفی در مدل به وجود میآید.
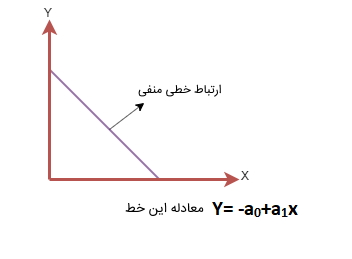
رگرسیون خطی چندگانه در یادگیری ماشین چیست ؟
در روش رگرسیون خطی چندگانه، بیش از یک متغیر مستقل برای مدل جهت پیدا کردن ارتباط وجود دارد. در معادله رگرسیون خطی چندگانه که در آن $$b_0 $$ نقطه قطع کردن است، $$b_1, b_2, b_3, b_4, … , b_n $$ ضرایب یا دامنههای متغیرهای مستقل $$x_1, x_2, x_3, x_4, … , x_n $$ هستند و $$y$$ یک متغیر وابسته به حساب میآید.
$$y = b_0 + b_1 x_1 + b_2 x_2 + b_3 x_3 + … + b_n x_n $$
اصطلاحات پیش بینی با استفاده از رگرسیون خطی در یادگیری ماشین
در این بخش با استفاده از مثال چند اصطلاح رایج در الگوریتمهای یادگیری ماشین و همچنین رگرسیون خطی آموزش داده شدهاند. در این مثال، تابع پیشبینی با استفاده از رگرسیون خطی، میتواند تخمینی از فروش را با توجه به هزینههای تبلیغات رادیویی شرکت و مقادیر فعلی برای «وزن» (Weight) و «بایاس» (Bias) به دست بیاورد. در ادامه رابطه ریاضی این مثال نشان داده شده است:
$$ Sales = Weight ⋅ Radio + Bias $$
در ادامه هر یک از مؤلفههای رابطه فوق بررسی و شرح داده شدهاند:
- وزن یا همان Weight: ضرایبی برای متغیر مستقل رادیو هستند. در یادگیری ماشین این ضرایب، وزن نامیده میشوند.
- رادیو یا همان Radio در فرمول فوق: ضرایب مستقلی هستند که در یادگیری ماشین به آنها ویژگی گفته میشود.
- بایاس یا همان Bias: به نقطهای که خط جدا کننده محور Yها را قطع میکند، در یادگیری ماشین بایاس گفته میشود. بایاس همه پیشبینیهای انجام شده را خنثی میکند.
کدهای رابطه فوق در ادامه نمایش داده شدهاند:
def predict_sales(radio, weight, bias):
return weight*radio + biasالگوریتم این مثال تلاش میکند تا مقدارهای صحیحی را برای وزن و بایاس یاد بگیرد. در انتهای یادگیری این الگوریتم، معادله خط مورد نظر بهترین برازش را به صورت تقریبی نشان میدهد. در ادامه بهترین خط برازش رگرسیون آموزش داده شده مشاهده میشود.
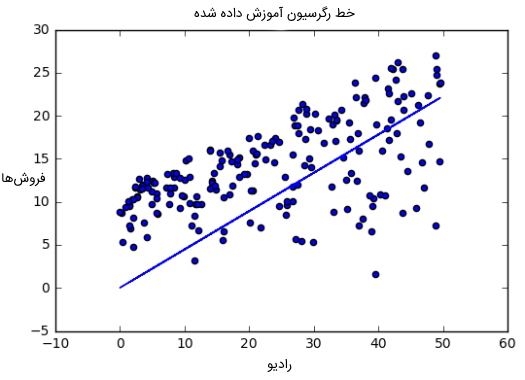
هدف الگوریتم رگرسیون خطی در یادگیری ماشین چیست ؟
هدف اصلی الگوریتمهای رگرسیون خطی، پیدا کردن بهترین خط برازش و مقدارهای بهینه برای جدا کنندهها و ضرایب از جمله به حداقل رساندن خطاها است. خطا در الگوریتمهای رگرسیون خطی، تفاوت بین مقدار واقعی و مقدار پیشبینی شده به حساب میآید و هدف الگوریتم کاهش این تفاوت است. در ادامه نموداری ارائه شده است که خطا را در یک الگوریتم رگرسیون خطی نشان میدهد.
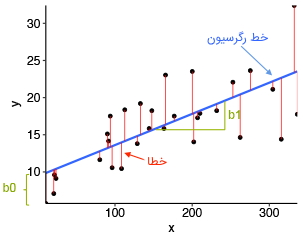
توضیحاتی در رابطه با نمودار فوق در ادامه فهرست شدهاند:
- x در نمودار فوق نشاندهنده متغیر وابسته است که روی محور Xها و y متغیر مستقل را نشان میدهد که روی محور Yها ترسیم شده است.
- نقطههای سیاه نشاندهنده نقاط داده یعنی همان مقدارهای واقعی هستند.
- $$ b_0 $$ فاصله جدا شده بین صفر تا ۱۰ و $$ b_1 $$ شیب متغیر x را نشان میدهد.
- خط آبی بهترین خط برازش پیشبینی توسط مدل رگرسیون خطی به حساب میآید. به عبارت دیگر، مقادیر پیشبینی شده روی خط آبی قرار دارند.
فاصله عمودی بین نقاط داده و خط رگرسیون به عنوان خطا یا باقیمانده شناخته میشود. هر نقطه داده دارای یک باقیمانده و مجموعه همه این تفاوتها به عنوان مجموع خطاها یا باقیماندهها در نظر گرفته شدهاند. رابطه ریاضی خطا برای الگوریتم رگرسیون خطی در ادامه نمایش داده شده است:
$$ Residual / Error = Actual values – Predicted Values $$
در فرمول فوق، خطا یا همان باقی مانده با استفاده از کم کردن مقدار واقعی از مقدار پیشبینی شده محاسبه شده است.
$$ Sum of Residuals / Errors = Sum ( Actual – Predicted Values)$$
مجموع مقادیر باقیمانده یا خطاها با استفاده از فرمول فوق به این صورت محاسبه شده است که مجموع مقادیر واقعی منهای مقادیر پیشبینی شده حساب میشود.
$$Square of Sum of Residuals / Errors = ( Sum ( Actual – Predicted Values) )^2$$
با استفاده از فرمول فوق، مربع مجموع خطا یا باقی مانده محاسبه میشود. در این رابطع، نتیجهای که از رابطه قبلی به دست آمده بود به توان دوم میرسد. رابطه زیر نشاندهنده فرمول ریاضی خطای کلی در الگوریتم رگرسیون خطی است:
$$sum e_i^2 = sum (Y _i – hat {Y_ i})$$
در بخش بعدی از مطلب «رگرسیون خطی در یادگیری ماشین»، پس از معرفی مجموعه دورههای آموزش «داده کاوی» (Data Mining) و یادگیری ماشین، به بررسی برخی از فرضیههای رگرسیون خطی پرداخته شده است.
معرفی فیلم های آموزش داده کاوی و یادگیری ماشین تم آف

دورههای آموزشی ویدیویی پلتفرم تم آف بر اساس موضوع به صورت مجموعههای آموزشی متفاوتی دستهبندی شدهاند. یکی از این مجموعههای جامع مربوط به دورههای آموزش داده کاوی و یادگیری ماشین است. علاقهمندان میتوانند از این مجموعه آموزشی برای مطالعه بیشتر استفاده کنند. در زمان تدوین این مطلب، مجموعه دورههای داده کاوی و یادگیری ماشین تم آف حاوی بیش از ۳۲۶ ساعت محتوای ویدیویی و حدود ۴۱ عنوان آموزشی مختلف بوده است. در ادامه این بخش، برخی از دورههای این مجموعه به طور خلاصه معرفی شدهاند:
- فیلم آموزش یادگیری ماشین Machine Learning با پایتون Python (طول مدت: ۱۰ ساعت، مدرس: مهندس سعید مظلومی راد): در این دوره آموزشی تم آف ابتدا سعی شده است، بستههای شناخته شده پایتون معرفی و سپس کار با توابع آنها آموزش داده شوند. در انتها نیز مباحث یادگیری ماشین همراه با مثالهای متعدد در پایتون مورد بررسی قرار گرفتهاند. برای مشاهده فیلم آموزش یادگیری ماشین Machine Learning با پایتون Python + کلیک کنید.
- فیلم آموزش یادگیری عمیق با پایتون – تنسورفلو و کراس TensorFlow و Keras (طول مدت: ۲ ساعت و ۵۷ دقیقه، مدرس: دکتر سعید محققی): در این دوره آموزشی، تمرکز بر روی آموزش محبوبترین ابزارهای نرم افزاری، پرکاربردترین کتابخانههای کدنویسی از جمله تنسورفلو و کراس و رایجترین مدلها و دادهها در زمینه یادگیری عمیق است. برای مشاهده فیلم آموزش یادگیری عمیق با پایتون – تنسورفلو و کراس TensorFlow و Keras + کلیک کنید.
- فیلم آموزش یادگیری عمیق – شبکه های GAN با پایتون (طول مدت: ۵ ساعت و ۶ دقیقه، مدرس: دکتر عادل قاضی خانی): در تم آف شبکههای GAN معمولی، شبکههای Deep Convolutional GAN ،Semi-Supervised GAN ،Conditional GAN و CycleGAN بررسی میشوند. علاوه بر این، قبل از ورود به حوزه شبکههای GAN، مفاهیم مقدماتی مورد نیاز یادگیری ماشین و شبکههای عصبی بیان شده است. در این آموزش از زبان پایتون برای برنامه نویسی شبکههای GAN استفاده میشود. برای مشاهده فیلم آموزش یادگیری عمیق – شبکه های GAN با پایتون + کلیک کنید.
- فیلم آموزش پردازش زبان های طبیعی NLP در پایتون Python با پلتفرم NLTK (طول مدت: ۷ ساعت و ۱۲ دقیقه، مدرس: مهندس احسان یزدانی): در این دوره آموزشی، زبان برنامه نویسی پایتون برای پردازش زبان طبیعی و مهمترین ابزار آن، یعنی NLTK آموزش داده شده است. برای مشاهده فیلم آموزش پردازش زبان های طبیعی NLP در پایتون Python با پلتفرم NLTK + کلیک کنید.
- فیلم آموزش کتابخانه scikit-learn در پایتون – الگوریتم های یادگیری ماشین (طول مدت: ۳ ساعت و ۵۷ دقیقه، مدرس: سید علی کلامی هریس): هدف این دوره آموزشی ویدویی، آموزش بخشی از الگوریتمهای یادگیری ماشین موجود در کتابخانه scikit-learn پایتون است. برای مشاهده فیلم آموزش کتابخانه scikit-learn در پایتون – الگوریتم های یادگیری ماشین + کلیک کنید.
- آموزش شبکه های عصبی پیچشی CNN – مقدماتی (طول مدت: ۲ ساعت و ۱۲ دقیقه، مدرس: سایه کارگری): از آنجا که شبکههای عصبی پیچشی یکی از نیازهای اصلی علاقهمندان به پردازش تصویر و بینایی ماشین به حساب میآیند، فراگیری مفاهیم این شبکهها از اهمیت بالایی برخوردار است و در این تم آف به آموزش آنها پرداخته میشود. برای مشاهده آموزش شبکههای عصبی پیچشی CNN – مقدماتی + کلیک کنید.
حال پس از معرفی مجموعه دورههای آموزش داده کاوی و یادگیری ماشین تم آف، بخش بعدی مطلب «رگرسیون خطی در یادگیری ماشین» به بررسی برخی از مفروضات این الگوریتم، اختصاص دارد.
فرضیه های رگرسیون خطی در یادگیری ماشین
الگوریتم رگرسیون خطی دارای برخی از فرضیهها و باورهایی است که مفاهیم بسیار سادهای هستند و در ادامه این بخش مورد بررسی قرار میگیرند.
خطی بودن در الگوریتم رگرسیون خطی چیست ؟
این خصوصیت الگوریتم رگرسیون خطی، بیان میکند که متغیر وابسته Y باید به صورت خطی با متغیرهای مستقل ارتباط داشته باشند. این فرض با رسم نمودار پراکندگی بین متغیرها بررسی و نمایش داده میشود.
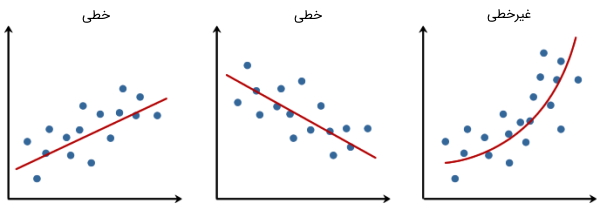
نرمال بودن در الگوریتم رگرسیون خطی چیست ؟
متغیرهای X و Y در الگوریتم رگرسیون خطی باید توزیع نرمالی داشته باشند. برای بررسی نرمال بودن دادهها و متغیرهای الگوریتم رگرسیون خطی میتوان از روشهای ترسیم هیستوگرام، KDE و Q-Q استفاده کرد. در ادامه نمودار هیستوگرام باقیمانده و «چندک» (Quantile) باقیمانده ارائه شده است.
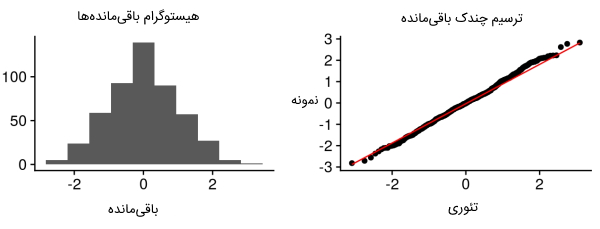
هم واریانسی در الگوریتم رگرسیون خطی چیست ؟
در الگوریتم رگرسیون خطی، واریانس عبارتهای دارای خطا باید ثابت باشد، به عبارت دیگر، نیاز است که گسترش باقیمانده برای همه متغیرهای X ثابت در نظر گرفته شود. این فرضیه را میتوان با رسم نمودار باقیمانده بررسی کرد. اگر این فرضیه انجام نشود و رد شود، نقاط داده به صورت قیف در نمودار جمع میشوند و اگر فرضیه به درستی انجام گیرد، نقاط داده ثابت خواهند بود. در ادامه نمودارهای باقیماندهها در شرایط مختلف برای الگوریتم رگرسیون خطی نمایش داده شدهاند:
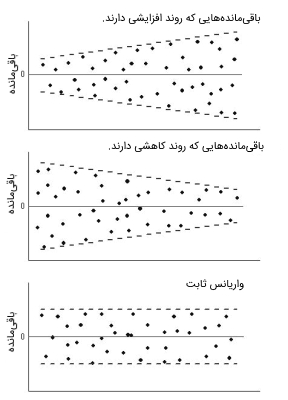
استقلال و غیر هم خطی چندگانه در الگوریتم رگرسیون خطی چیست ؟
فرضیه استقلال و غیر هم خطی چندگانه در الگوریتم رگرسیون خطی بیان میکند که متغیرها باید نسبت به یکدیگر مستقل باشند؛ به عبارت دیگر نباید بین متغیرهای مستقل «همبستگی» (Correlation) وجود داشته باشد. برای بررسی این موضوع میتوان از «ماتریس همبستگی» (Correlation Matrix) یا معیار VIF استفاده کرد. اگر معیار VIF بزرگتر از ۵ باشد، متغیرها همبستگی بالایی دارند. در تصویر زیر همبستگی بالایی بین متغیرهای سطر x5 و x6 وجود دارد.
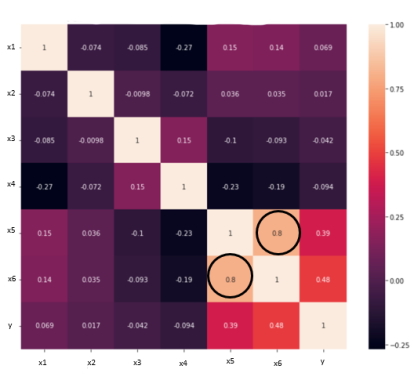
رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده
نداشتن خود همبستگی در الگوریتم رگرسیون خطی چیست ؟
عبارتهای خطا باید مستقل از یکدیگر باشند. خود همبستگی را میتوان با استفاده از «آزمون دوربین واتسون» (Durbin Watson Test) بررسی کرد. فرضیه «تهی» (Null) فرض میکند که هیچ خود همبستگی در الگوریتم وجود ندارد. به طور کلی مقدار این آزمون ۰ تا ۴ است و اگر مقدار ۴ باشد، هیچ خود همبستگی وجود ندارد.
چگونه می توان بهترین خط برازش را در رگرسیون خطی پیدا کرد؟
زمانی که فرد با رگرسیون خطی در حال کار کردن است، مهمترین هدف پیدا کردن بهترین خط برازش به حساب میآید. به عبارت دیگر، هدف یافتن خطی است که کمترین خطا را بین مقدارهای پیشبینی شده و مقدارهای واقعی داشته باشد. بنابراین بهترین خط برازش، خطی است که کمترین خطا را دارد. مقدارهای مختلف موجود برای وزنها و ضرایب خطهای $$ (a_0 , a_1)$$ باعث ایجاد خطهای رگرسیون مختلفی میشود. بنابراین، نیاز است که بهترین مقدار برای $$ a_0 $$ و $$ a_1 $$ به منظور پیدا کردن مناسبترین خط برازش محاسبه شود. از این رو، برای محاسبه این مقدار از «تابع هزینه» (Cost Function) استفاده میشود که در ادامه به آن پرداختهایم.
تابع زیان یا تابع هزینه چیست؟
تابع هزینه یا همان تابع زیان به توسعه دهندگان این امکان را میدهد تا با استفاده از آن بهترین مقدار ممکن را برای $$ a_0 $$ و $$ a_1 $$ پیدا کنند و بهترین و مناسبترین خط برازش را برای نقاط داده فراهم میکند. از آنجایی که مدل نیازمند بهترین مقدار برای $$ a_0 $$ و $$ a_1 $$ است، میتوان این مسئله را به عنوان یک مسئله کمینهسازی در نظر گرفت و خطای بین مقدار واقعی و مقدار پیشبینی شده را به حداقل رساند.
توابع زیان (Loss Function) در یادگیری ماشین – به همراه کدهای پایتون
در تصویر زیر معادله ریاضی تابع هزینه نمایش داده شده است:
$$minimize = frac 1n sum_ {i=1} ^ {n} {(pred _i – y _i)}^2$$
$$J = frac 1n sum_ {i=1} ^ {n} {(pred _i – y _i)}^2$$
تابع فوق برای کمینهسازی خطا انتخاب میشود. برای محاسبه این مقدار میبینیم، اختلاف خطای بین مقدارهای واقعی و پیشبینی شده به توان ۲ رسانده شدهاند، این مقدار برای تمام نقاط داده، محاسبه و باهم جمع میشوند و در نهایت مقدار به دست آمده، بر تعداد کل نقاط داده تقسیم خواهند شد. به عبارت دیگر، رابطه تابع هزینه میانگین مربع مقدار خطا برای همه نقاط داده را فراهم میکند. بنابراین، این تابع هزینه به عنوان تابع «میانگین مربعهای خطا» (Mean Squared Error | MSE) نیز شناخته میشود. حال، با استفاده از این تابع MSE، مقادیر $$ a_0 $$ و $$ a_1 $$ طوری تغییر داده میشوند که مقدار MSE در حالت مینیمم قرار بگیرد.
بررسی معیارهای ارزیابی رگرسیون در پایتون — پیاده سازی + کدها
میتوان کدهای زبان برنامه نویسی «پایتون» (Python) تابع هزینه را به صورت زیر نوشت:
def cost_function(radio, sales, weight, bias):
companies = len(radio)
total_error = 0.0
for i in range(companies):
total_error += (sales[i] - (weight*radio[i] + bias))**2
return total_error / companiesگرادیان کاهشی چیست؟
مفهوم دیگری که باید در رگرسیون خطی آن را درک کرد، «گرادیان کاهشی» (Gradient Descent) است. گرادیان کاهشی روشی برای بهروزرسانی $$ a_0 $$ و $$ a_1 $$ برای کاهش مقدار تابع هزینه یا همان MSE به حساب میآید. ایده این روش به این صورت است که در ابتدا کار با مقادیری برای $$ a_0 $$ و $$ a_1 $$ شروع میشود و سپس کم کم این مقدار را باید تغییر داد تا مقدار تابع هزینه کاهش پیدا کند. به طور کلی گرادیان کاهشی امکان تغییر مقادیر را به توسعه دهندگان میدهد. در تصویر زیر تاًثیر انواع «نرخ یادگیری» (Learning Rate) روی دو نمودار مشابه نمایش داده شده است.
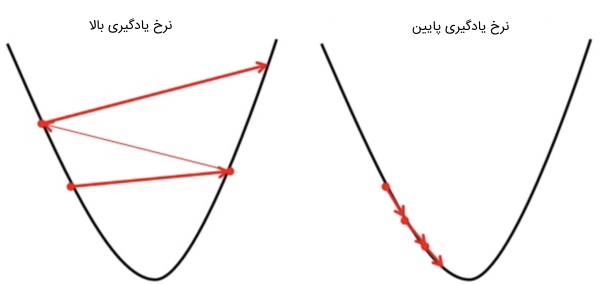
برای درک بهتر نرخ یادگیری، میتوان گودالی شبیه به U تصور کرد و در بالاترین نقطه گودال ایستاد و هدف را رسیدن به انتهای گودال در نظر گرفت. برای رسیدن به انتهای گودال فقط باید تعداد معینی قدم برداشت. اگر فرد تصمیم بگیرید در هر بار فقط یک قدم بردارد، زمان زیادی برای رسیدن به انتهای گودال صرف میشود. اما اگر هر بار قدم بزرگتری برداشت، احتمال این وجود دارد که زودتر به انتهای گودال رسید، اما احتمال دیگری نیز وجود دارد و آن هم این است که با برداشتن گامهای بزرگ ممکن است نتوان در محل مورد نظر یعنی نقطه مینیمم توقف کرد و عبور از آن نقطه اتفاق بیوفتد.
در الگوریتم گرادیان کاهشی، تعداد قدمهایی که برداشته میشود، همان نرخ یادگیری هستند و این نرخ یادگیری مشخص میکند که الگوریتم باید با چه سرعتی به سمت مینیمم همگرا شود. گاهی اوقات تابع هزینه میتواند تابع غیر محدبی باشد که میتوان در آن، در بخش مینیمم محلی قرار گرفت، اما برای الگوریتم رگرسیون خطی در یادگیری ماشین همیشه این تابع، محدب است. تصویر زیر تابع محدب و غیرمحدب را نشان میدهد.
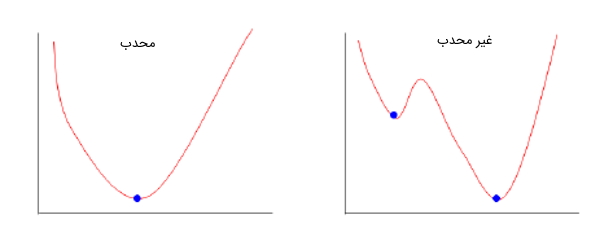
حال باید به این موضوع پرداخت که چطور میتوان با استفاده از گرادیان کاهشی، مقدارهای $$ a_0 $$ و $$ a_1 $$ را بهروزرسانی کرد. برای بهروزرسانی $$ a_0 $$ و $$ a_1 $$ مقدار گرادیانها از تابع هزینه گرفته میشوند. برای پیدا کردن این مقادیر گرادیانها، مشتق جزئی یا همان نسبی با توجه به $$ a_0 $$ و $$ a_1 $$ از تابع گرفته میشود. حال، برای درک اینکه چطور میتوان این مشتق جزئی را محاسبه کرد، اثبات این موضوع در ادامه ارائه شده است:
$$J = frac 1n sum_ {i=1} ^ {n} {(pred _i – y _i)}^2$$
$$J = frac 1n sum_ {i=1} ^ {n} {(a _0 + a _1 . x _i – y_ i)}^2$$
$$ frac {partial J} {partial a_0} = frac 2n sum_ {i=1} ^ {n} (a_0 + a_1 . x _i – y _i) Longrightarrow frac {partial J} {partial a_0} = frac 2n sum_ {i=1} ^ {n} (pred _i – y _i)$$
$$ frac {partial J} {partial a_0} = frac 2n sum_ {i=1} ^ {n} (a_0 + a_1 . x _i – y _i). x_ i Longrightarrow frac {partial J} {partial a_0} = frac 2n sum_ {i=1} ^ {n} (pred _i – y _i). x_ i$$
رابطه نهایی ارائه شده برای مقدار گرادیانها در تصویر زیر نمایش داده شده است:
$$a_0 = a_0 – alpha. frac 2n sum_ {i=1} ^ {n} (pred _i – y _i)$$
$$a_1 = a_1 – alpha. frac 2n sum_ {i=1} ^ {n} (pred _i – y _i). x_ i$$
مشتقات جزئی گرادیانها برای بهروزرسانی مقدار $$ a_0 $$ و $$ a_1 $$ استفاده میشوند. آلفا در معادلههای بالا نشاندهنده نرخ یادگیری یا «فراپارامترهایی» (Hyperparameter) است که باید مشخص شوند. اگر مقدار نرخ یادگیری کم باشد، به مقدار تابع هزینه مینیمم نزدیکتر خواهد بود، اما زمان بیشتری برای رسیدن به این مقدار صرف میشود. همچنین، اگر مقدار نرخ یادگیری بالا باشد، تابع زودتر همگرا خواهد شد، اما ممکن است مقدار نهایی از مینیمم مورد نظر کمتر شود.
برای حل گرادیان کاهشی با استفاده از کدهای پایتون، نقاط داده الگوریتم با استفاده از وزن جدید و مقادیر بایاس تکرار میشوند و میانگین مشتقات جزئی محاسبه خواهند شد. نتایج گرادیان شیب تابع هزینه در موقعیت فعلی (یعنی وزن و بایاس) مسیری را نشان میدهد که باید با استفاده از آن تابع هزینه را کاهش داد (یعنی حرکت در جهت مخالف گرادیان). همچنین اندازه بهروزرسانی با استفاده از نرخ یادگیری کنترل میشود. در ادامه کدهای پیادهسازی گرادیان کاهشی با پایتون نمایش داده شدهاند.
def update_weights(radio, sales, weight, bias, learning_rate):
weight_deriv = 0
bias_deriv = 0
companies = len(radio)
for i in range(companies):
# Calculate partial derivatives
# -2x(y - (mx + b))
weight_deriv += -2*radio[i] * (sales[i] - (weight*radio[i] + bias))
# -2(y - (mx + b))
bias_deriv += -2*(sales[i] - (weight*radio[i] + bias))
# We subtract because the derivatives point in direction of steepest ascent
weight -= (weight_deriv / companies) * learning_rate
bias -= (bias_deriv / companies) * learning_rate
return weight, biasمنظم سازی یا Regularization چیست؟
افزونههای گسترده زیادی برای آموزش مدل خطی به نام متدهای «Regularization» یا همان «منظمسازی» وجود دارند. این روشها نیز برای به حداقل رساندن مجموعه مربعات خطاهای مدل در دادههای آموزشی استفاده میشوند و معمولاً از روش «حداقل مربعات عادی» (Ordinary Least Squares) استفاده میکنند. وقتی بیش از یک ورودی وجود داشته باشد، میتوان از روش حداقل مربعات عادی برای پیشبینی مقادیر ضرایب استفاده کرد. به عبارت دیگر، با استفاده از یک خط رگرسیون به دست آمده از طریق دادهها، فاصله هر نقطه داده تا خط رگرسیون محاسبه میشود، سپس توان ۲ یا همان مربع این فاصله محاسبه خواهد شد و پس از آن، تمام مربعات خطاها با یکدیگر جمع میشوند.
این کمیتی است که روش حداقل مربعات عادی قصد دارد آن را به حداقل برساند. یعنی این روش به دنبال به حداقل رساندن مجموع مربع باقیمانده است. همچنین این روشها به دنبال کاهش پیچیدگی مدل با استفاده از تعداد یا اندازه مطلق مجموعه همه ضرایب در مدل هستند. دو مثال رایج و محبوب از روشهای Regularization برای رگرسیون خطی در یادگیری ماشین در ادامه ارائه شدهاند:
- «رگرسیون لاسو» (Lasso Regression): در این روش از متد حداقل مربعات عادی برای به حداقل رساندن مجموع ضرایب مطلق استفاده میشود و این روش با نام «L1 regularization» شناخته شده است.
- «رگرسیون ستیغی» (Ridge Regression): در این روش از متد حداقل مربعات عادی برای به حداقل رساندن مجموع مربعات ضرایب مطلق استفاده شده است و این روش به عنوان «L2 regularization» شناخته میشود.
این روشها برای استفاده در زمانی مناسب هستند که «همخطی» (Collinearity) در مقادیر ورودی وجود داشته باشد و حداقل مربعات عادی با دادههای آموزشی دارای «بیشبرازش» یا همان «Overfit» باشند.
هم خطی در مدل رگرسیونی — به زبان ساده
آماده سازی داده ها برای رگرسیون خطی در یادگیری ماشین چگونه است؟
تحقیقات زیادی در رابطه با رگرسیون خطی در یادگیری ماشین انجام شده است و روشهای بسیاری درباره نحوه ساختار استفاده از دادهها برای رسیدن به مدلی بهینه وجود دارند. به طور کلی رایجترین روش پیادهسازی رگرسیون خطی، «حداقل مربعات عادی» به حساب میآید و میتوان از قوانین آن استفاده بسیاری کرد. برخی از روشهای آمادهسازی دادهها در الگوریتم رگرسیون خطی در ادامه ارائه شدهاند که میتوان بر اساس نوع مسئله خود مناسبترین روش را برای آمادهسازی دادهها انتخاب کرد:
- «فرضیه خطی» (Linear Assumption): در الگوریتم رگرسیون خطی فرض میشود که رابطه بین ورودیها و خروجیها به صورت خطی است. چیز دیگری نیز در این الگوریتم پشتیبانی نمیشود. زمانی که ویژگیهای مدل زیاد هستند باید به این موضوع توجه شود و ممکن است نیاز باشد که دادههای مدل را تبدیل کرد. برای مثال میتوان تبدیل لگاریتم به تابع نمایی را در نظر گرفت.
- «حذف نویز» (Remove Noise): در رگرسیون خطی فرض میشود که متغیرهای وروردی و خروجی نویزدار نیستند. روشهای پاکسازی دادهها برای داشتن دادههایی بهتر و واضح مورد استفاده قرار میگیرند. این روش برای متغیرهای خروجی دارای اهمیت بالایی است و میتوان در صورت امکان «مقادیر پرت» (Outlier) متغیر خروجی (y) را حذف کرد.
- «حذف همخطی» (Remove Collinearity): زمانی که در دادههای ورودی همبستگی بالایی وجود داشته باشد، الگوریتم رگرسیون خطی دچار بیشبرازش در دادهها میشود. برای رفع این مسئله میتوان محاسبه همبستگیهای دو به دو در دادههای ورودی و حذف بیشترین همبستگیها را در نظر گرفت.
- «توزیع گوسی» (Gaussian Distribution): اگر ورودی و خروجیهای مدل دارای توزیع گوسی باشند، رگرسیون خطی میتواند پیشبینیهای قابل اعتمادتری را ارائه دهد. ممکن است بتوان با تبدیلهایی از جمله تبدیل لگاریتمی و BoxCox روی متغیرهای مدل خود، مزایایی را به دست آورد تا توزیع متغیرها بیشتر به شکل توزیع گوسی شوند.
- «تغییر مقیاس ورودیها» (Rescale Input): اگر متغیرهای ورودی مدل با استفاده از روشهای «استانداردسازی» (Standardization) و «نرمالسازی» (Normalization) تغییر مقیاس داده شوند، الگوریتم رگرسیون خطی میتواند پیشبینیهای قابل اعتمادتری را ارائه دهد.
در بخش بعدی از مقاله «رگرسیون خطی در یادگیری ماشین» به بررسی کدهایی از این الگوریتم پرداخته شده است.
کدهای رگرسیون خطی در یادگیری ماشین
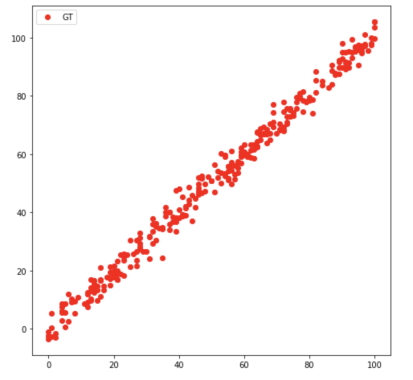
برای ایجاد کدهای الگوریتم رگرسیون خطی در یادگیری ماشین دو روش وجود دارد. روش اول این است که از کتابخانه «Scikit Learn» پایتون استفاده شود و مدل رگرسیون خطی از این کتابخانه «Import» یا همان وارد برنامه شود و به صورت مستقیم مورد استفاده قرار گیرد. روش دوم این است که الگوریتم رگرسیون خطی در یادگیری ماشین خود را با استفاده از معادلههای بالا به صورت دستی بنویسیم. در این بخش هر دوی این روشها شرح داده شدهاند. مجموعه دادههای زیادی به صورت آنلاین برای رگرسوین خطی در دسترس هستند. در کدهای زیر از مجموعه داده وب سایت «Kaggle» [+] استفاده شده است. دادههای بخش «آموزش» به صورت زیر مصورسازی شدهاند:
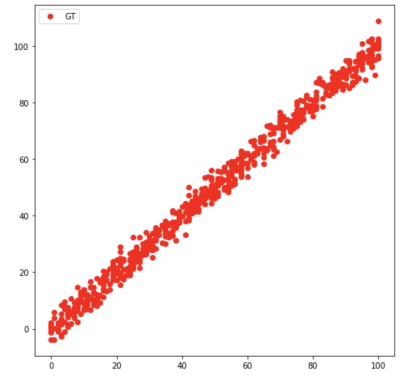
همچنین، دادههای بخش «تست» الگوریتم رگرسیون خطی در یادگیری ماشین نیز به صورت زیر نشان داده میشوند:
پیاده سازی رگرسیون خطی در یادگیری ماشین با کتابخانه Scikit Learn پایتون
در این بخش ابتدا سادهترین راه حل برای ایجاد الگوریتم رگرسیون خطی در یادگیری ماشین شرح داده میشود. این راه حل استفاده از کتابخانه «Scikit Learn» پایتون برای ساخت یک مدل رگرسیون خطی است که کدهای آن در ادامه نمایش داده شدهاند:
import pandas as pd
import numpy as np
df_train = pd.read_csv('/Users/FaraDars/Documents/Datasets/Linear_Regression/train.csv')
df_test = pd.read_csv('/Users/FaraDars/Documents/Datasets/Linear_Regression/test.csv')
x_train = df_train['x']
y_train = df_train['y']
x_test = df_test['x']
y_test = df_test['y']
x_train = np.array(x_train)
y_train = np.array(y_train)
x_test = np.array(x_test)
y_test = np.array(y_test)
x_train = x_train.reshape(-1,1)
x_test = x_test.reshape(-1,1)ابتدا در کدهای فوق، از کتابخانه «Pandas» پایتون برای خواندن مجموعه دادههای آموزش و تست استفاده شده است. متغیرهای مستقل (x) و وابسته (y) بازیابی میشوند و از آنجایی که فقط یک ویژگی (x) وجود دارد، تغییر شکل یا همان «Reshape» متغیرها به گونهای انجام میشود که بتوان از آنها به عنوان وروردی الگوریتم رگرسیون خطی استفاده کرد. ادامه کدهای این پیادهسازی در ادامه ارائه شدهاند:
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
clf = LinearRegression(normalize=True)
clf.fit(x_train,y_train)
y_pred = clf.predict(x_test)
print(r2_score(y_test,y_pred))در کدهای فوق از کتابخانه «Scikit Learn» برای وارد کردن مدل رگرسیون خطی در یادگیری ماشین استفاده شده است. سپس، مدل دادههای آموزشی را به عنوان وروردی دریافت میکند و مقادیر دادههای تست را پیشبینی خواهد کرد. در این روش، برای اندازهگیری دقت پیشبینی مدل، از معیار «R2 score» استفاده شده است و دقتی که این مدل ارائه میدهد روی دادههای تست به صورت نیز نمایش داده میشود:
R2 Score: 0.98880231503
پیاده سازی رگرسیون خطی در یادگیری ماشین با برنامه نویسی معادله اصلی آن
حال، در ادامه این بخش از مطلب «رگرسیون خطی در یادگیری ماشین» مدل رگرسیون خطی با معادلههای ارائه شده در توضیحات مفاهیم این مطلب برای رگرسیون خطی ایجاد و نوشته میشود. در این کدها فقط نیاز است که از کتابخانه «Numpy» پایتون برای محاسبات و «R2 score» برای نشان دادن معیار دقت استفاده شود. کدهای این برنامه در ادامه ارائه شدهاند:
## Linear Regression
import numpy as np
n = 700
alpha = 0.0001
a_0 = np.zeros((n,1))
a_1 = np.zeros((n,1))
epochs = 0
while(epochs در کدهای فوق مقدار 0.0 در متغیرهای a_0 و a_1 مقداردهی اولیه شده است. تعداد «ایپاک» (Epoch) یا هر دوره در مدل برابر با ۱۰۰۰ در نظر گرفته میشود و برای ۱۰۰۰ ایپاک هزینه محاسبه شده است و این هزینه محاسبه شده در گرادیانها مورد استفاده قرار میگیرد. سپس از این مقدارهای گرادیانها برای بهروزرسانی مقدارهای a_0 و a_1 استفاده میشود. در این مدل رگرسیون خطی پس از ۱۰۰۰ ایپاک، بهترین مقدار برای متغیرهای a_0 و a_1 به دست میآید و با استفاده از آنها میتوان بهترین خط صاف برازش را ایجاد کرد. در ادامه کدهای بخش تست این مدل ارائه شده است:
import matplotlib.pyplot as plt
y_prediction = a_0 + a_1 * x_test
print('R2 Score:',r2_score(y_test,y_prediction))
y_plot = []
for i in range(100):
y_plot.append(a_0 + a_1 * i)
plt.figure(figsize=(10,10))
plt.scatter(x_test,y_test,color='red',label='GT')
plt.plot(range(len(y_plot)),y_plot,color='black',label = 'pred')
plt.legend()
plt.show()مجموعه داده تست برای این مدل رگرسیون خطی شامل ۳۰۰ نمونه است. بنابراین، باید متغیرهای $$ a_0 $$ و $$ a_1 $$ از اندازه 700×1
به 300×1
تغییر شکل بدهند. حال، فقط از معادله رگرسیون خطی برای پیشبینی مقدار در مجموعه داده تست استفاده میشود و این دقت پیشبینی دقیقاً مانند روش قبلی با استفاده از R2 score نمایش داده شده و نتیجه آن به صورت زیر ارائه شده است.
R2 Score: 0.98880231503
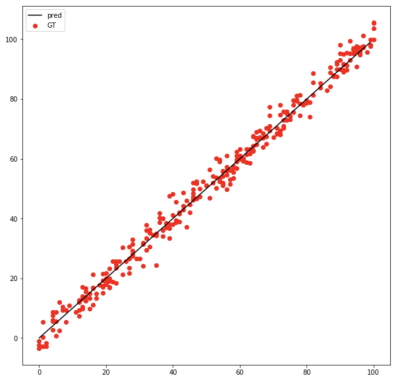
مشاهده میشود که برای این مجموعه داده و روش برنامه نویسی رگرسیون خطی در یادگیری ماشین، دقت پیشبینی دقیقاً مانند روش اول است. همچنین، خط رگرسیون روی نقاط داده مجموعه تست برای درک تصویری بهتر از روش عملکرد این الگوریتم در تصویر زیر نمایش داده میشود:
معیارهای ارزیابی برای تجزیه و تحلیل رگرسیون
برای درک و فهمیدن سطح کارایی یک مدل رگرسیون خطی نیاز است آن را با معیاری ارزیابی کرد. در این بخش از مطلب «رگرسیون خطی در یادگیری ماشین» انواع معیارهای ارزیابی برای تجزیه و تحلیل رگرسیون مورد بررسی قرار میگیرند. ابتدا به بررسی مربع R یا «ضریب تعیین» (Coefficient of Determination) پرداخته میشود.
معیار مربع R یا ضریب تعیین برای ارزیابی رگرسیون خطی در یادگیری ماشین
رایجترین معیار ارزیابی مدلهای رگرسیون خطی در یادگیری ماشین، مربع R یا ضریب تعیین به حساب میآید. میتوان این معیار را به عنوان نسبت تغییرات به کل تغییرات تعریف کرد. مقدار «مربع R» یا همان «R squared» بین صفر تا یک است و هر چه مقدار دقت مدل با این معیار به یک نزدیکتر باشد، مدل دقت بالاتری دارد و مدل بهتری در نظر گرفته میشود. در ادامه معادله این معیار ارزیابی ارائه شده است.
$$R^2 = 1 – frac {SS_ {RES}} {SS_ {TOT}} = frac { sum _i (y_ i – hat {y _i})^2} {sum _i (y _i – overline{y})^2}$$
در معادله فوق، $$SS _ {RES}$$ نشاندهنده مجموعه باقیمانده مربعها و $$SS _ {TOT}$$ مجموعه همه مربعها به حساب میآیند.
معیار مربع R تنظیم شده برای ارزیابی رگرسیون خطی در یادگیری ماشین
معیار ارزیابی «مربع R تنظیم شده» ( Adjusted R squared) نوع بهبود یافته معیار ارزیابی مربع R به حساب میآید. مشکلی که روش R۲ دارد این است که با افزایش ویژگیهای مدل، مقدار R2 نیز افزایش مییابد که البته باعث به وجود آمدن مدل خوبی نیز میشود. اما مربع R تنظیم شده برای حل این مشکل ارائه شده است. این روش فقط ویژگیهایی را در نظر میگیرد که برای مدل مهم هستند و بر این اساس میتواند بهبود واقعی مدل را نشان دهد. همچنین، معیار R تنظیم شده همیشه از معیار R2 کمتر است. در تصویر زیر معادله این معیار نمایش داده میشود.
$$R^2 adjusted = 1- frac {(1 – R^2)(N -1)} {N – P- 1}$$
در رابطه فوق، $$R^2$$ نشاندهنده تعداد نمونههای مربع R، آرگومان p نشاندهنده تعداد پیشبینیها و N اندازه نمونههای کل هستند.
معیار میانگین مربع های خطا برای ارزیابی رگرسیون خطی در یادگیری ماشین
یکی دیگر از معیارهای رایج برای ارزیابی رگرسیون خطی در یادگیری ماشین، «میانگین مربعهای خطا» (Mean Squared Error | MSE) است که میانگین اختلاف مربع مقادیر واقعی و پیشبینی شده را نشان میدهد. رابطه این معیار در ادامه نمایش داده میشود:
$$MSE = frac 1n sum (y – hat {y})^2 $$
بخش داخل پرانتز رابطه فوق، نشاندهنده مربع تفاوت بین مقدارهای واقعی و مقدارهای پیشبینی شده است.
معیار ریشه میانگین مربعات خطا برای ارزیابی رگرسیون خطی در یادگیری ماشین
این معیار «ریشه معیار میانگین مربعات خطا» (Root Mean Squared Error | RMSE) به حساب میآید. به عبارت دیگر، میتوان گفت که ریشه میانگین تفاوت مقدارهای واقعی و پیشبینی شده است. RMSE در بررسی خطاهای بزرگ مورد استفاده قرار میگیرد، با اینکه MSE به این صورت نیست. رابطه این معیار در ادامه نمایش داده شده است:
$$RMSE = sqrt {{ frac 1n sum_ {i=1} ^ {n}} (y _i – hat {y _i})^2} $$
جمعبندی
رگرسیون خطی نوعی الگورتیم در یادگیری ماشین به حساب میآید که هر متخصصی در این حوزه باید با آن آشنا باشد. همچنین میتوان از این الگوریتم به عنوان نقطه شروع خوبی برای یادگیری ماشین لرنینگ استفاده کرد. الگوریتم رگرسیون خطی در یادگیری ماشین بسیار ساده و سودمند است. در این مطلب سعی شد به طور جامع به این سوال پاسخ داده شود که رگرسیون خطی در یادگیری ماشین چیست.
همچنین، بیشتر مسائل مورد نیاز و مرتبط با این الگوریتم از جمله روشهای استفاده، آمادهسازی دادهها و بررسی انواع معیارها همراه با کدهای پایتون مورد بررسی قرار گرفتند. در نهایت برخی از آموزشهای ویدیویی تم آف در زمینه یادگیری ماشین در این مطلب به علاقهمندان و دانشجویان معرفی شدند.

