حذف روند سری های زمانی در پایتون — راهنمای گام به گام

در آموزشهای قبلی مجله تم آف، با تحلیل سری زمانی آشنا شدیم. در این آموزش، روش حذف روند سری های زمانی در پایتون را شرح میدهیم.

روشهای حذف روند سری های زمانی
دادههای سری زمانی (Time Series) به طور کلی از ۵ بخش تشکیل شدهاند:
- سطح یا Level: نشاندهنده سطح و میانگین مقادیر دادهها است که با L نشان میدهیم.
- روند یا Trend: نشاندهنده تمایل سری زمانی به حرکت در یک جهت و بعضاً ثابت ماندن است که آن را با T نشان میدهیم.
- تناوب یا Cyclic: تغییرات یکسان و تکراری است که در فاصلههای منظمی تکرار میشود و آن را با C نشان میدهیم.
- فصلی یا Seasonal: تغییراتی که در فواصل کمتر از یک دوره و تناوب ایجاد میشوند که آن را با S نشان میدهیم.
- تغییرات نامعمول یا Irregular: تغییراتی که به صورت نامنظم رخ میدهند و با دادههای موجود قابل پیشبینی نیستند، بنابراین تصادفی در نظر گرفته میشوند و با I نشان داده میشود.
برای انجام یک تحلیل مناسب، نیاز داریم تا هر مؤلفه را شناسایی و جدا کنیم و در نهایت از ترکیب آنها برای انجام پیشبینی مناسب استفاده کنیم. ترکیب مؤلفههای گفته شده، میتواند به ۳ شکل زیر انجام شود:
1. مدل جمعی (Additive Model):
$$Y_{t}=L+T_{t}+C_{t}+S_{t}+I_{t}$$
2. مدل ضربی (Multiplicative Model):
$$Y_{t}=L cdot T_{t} cdot C_{t} cdot S_{t} cdot I_{t}$$
3. مدل لگاریتم جمعی (Log-Additive Model):
$$Y_{t}=e^{L+T_{t}+C_{t}+S_{t}+I_{t}}$$
در ادامه این مطلب، به روشهای «حذف روند» (Detrending) میپردازیم. به این منظور، روشهای زیر را بررسی خواهیم کرد:
- «تفاضلگیری» (Differentiation)
- «میانگین متحرک» (Moving Average)
- مدلسازی روند با استفاده از «رگرسیون» (Regression)
- «فیلتر هودریک-پرِسکات» (Hodrick-Prescott Filter)
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
حذف روند سری های زمانی در پایتون
قبل از شروع، کتابخانههای مورد نیاز را فراخوانی و تنظیمات مورد نیاز را اعمال میکنیم:
import numpy as np
import yfinance as yf
import matplotlib.pyplot as plt
import sklearn.linear_model as lm
import statsmodels.tsa.filters.hp_filter as hpاین کتابخانهها به ترتیب برای موارد زیر استفاده خواهند شد:
- محاسبات برداری و کار با آرایهها
- دریافت دادههای مالی به صورت آنلاین (Online)
- رسم نمودار دادهها
- ایجاد و آموزش مدلهای خطی
- فیلتر هودریک پرسکات
روش تفاضلگیری
یک سری زمانی با فرمول زیر ایجاد میکنیم:
$$ Y_{t}=5 sin (4 times t)+e^{frac{t}{4}}+I_{t} $$
در این رابطه عبارت $$I_t$$ نشاندهنده رفتارهای نامنظم است.
این سری را در بازه $$[0,4π]$$ به شکل زیر ایجاد میکنیم:
T1 = np.linspace(start=0, stop=4*np.pi, num=160)
S1 = 5 * np.sin(4 * T1) + np.exp(T1 / 4) + np.random.normal(loc=0, scale=0.1, size=(T1.size, ))حال نمودار این سری زمانی را به شکل زیر رسم میکنیم:
plt.plot(T1, S1, lw=1, c='crimson')
plt.title('S1')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()که شکل زیر را خواهیم داشت.
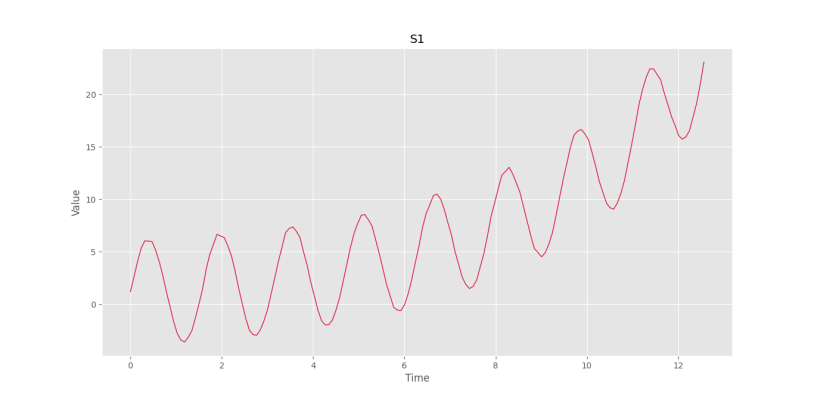
مشاهده میکنیم یک سری زمانی با روند نمایی ایجاد میشود.
برای حذف روند به روش تفاضلگیری، میتوانیم به شکل زیر تابعی تعریف کنیم که با گرفتن سری زمانی و فاصله تفاصلگیری، اختلاف را محاسبه و برگرداند:
def Diff(S:np.ndarray, L:int=1):
D = S[L:] - S[:-L]
return Dحال برای این مجموعه داده، تفاصل هر داده با داده قبلی را محاسبه میکنیم و نمایش میدهیم:
D1 = Diff(S1)
plt.plot(T1[-D1.size:], D1, lw=1, c='crimson')
plt.title('D1')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()که برای کد فوق، نمودار زیر حاصل میشود.

به این ترتیب، مشاهده میکنیم که بخش زیادی از روند دادهها حذف و یک سری زمانی ایستا (Stationary) حاصل شده است. توجه داشته باشید که در برخی مواقع نیاز است تا چندین بار تفاضلگیری انجام دهیم یا تفاضلگیری با طول بیشتر از ۱ انجام دهیم. برای مثال اگر برای سری فوق، تفاضلگیری را با دادههایی به جز دوره قبل انجام دهیم، به احتمال زیاد نتایج مطلوبی نخواهیم گرفت.
میانگین متحرک
میانگینهای متحرک به دلیل اینکه با استفاده از دادههای $$L$$ قبل محاسبه میشوند و در مقابل تغییرات دیرتر واکنش نشان میدهند، میتوانند به عنوان روند استفاده شوند و مزیت مهم آنها، قابلیت تنظیم طول بازه و انواع مختلف آنها است. به همین منظور، میتوان آنها را به عنوان روند در نظر گرفت و از سری زمانی حذف کرد.
برای آشنایی بیشتر با میانگین متحرک میتوانید به مطلب «میانگین متحرک چیست؟ پیادهسازی میانگین متحرک (Moving Average) در پایتون» مراجعه کنید.
حال به عنوان داده، از قیمت بیتکوین (Bitcoin) در ۱ سال اخیر استفاده میکنیم:
DF2 = yf.download(tickers='BTC-USD', period='1y', interval='1d')
S2 = DF2['Close'].to_numpy()حال نمودار را برای این دادهها تکرار میکنیم:
T2 = np.arange(start=0, stop=S2.size)
plt.plot(T2, S2, lw=1, c='crimson')
plt.title('S2')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()که شکل زیر را خواهیم داشت.
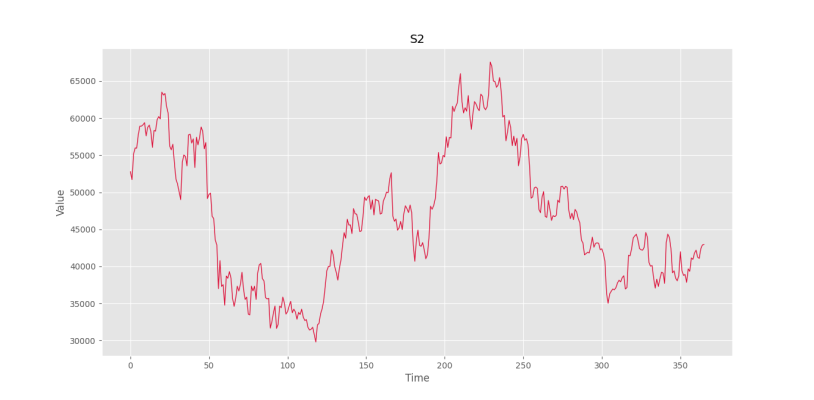
به این ترتیب، روندهای داده به شکل زیر قابل تشخیص است:
- افزایش: روز ۱۲۰ تا ۱۷۰ – روز ۱۸۵ تا ۲۳۰
- خنثی: روز ۰ تا ۴۵ – روز ۳۰۵ تا ۳۶۵
- کاهشی: روز ۴۵ تا ۱۲۰ – روز ۱۷۰ تا ۱۸۵ – روز ۲۳۰ تا ۳۰۵
حال میتوانیم یک تابع برای میانگین متحرک ساده (SMA) به شکل زیر پیادهسازی کنیم:
def SMA(S:np.ndarray, L:int):
nD0 = np.size(S)
nD = nD0 - L + 1
sma = np.zeros(nD)
for i in range(nD):
sma[i] = np.mean(S[i:i + L])
return smaحال میتوانیم میانگین متحرک را اعمال کنیم و سپس در یک نمودار نشان دهیم:
M2 = SMA(S2, 10)
plt.plot(T2, S2, lw=0.9, c='crimson', label='S2')
plt.plot(T2[-M2.size:], M2, lw=1, c='teal', label='M2')
plt.title('S2 + M2')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()که در این صورت، نمودار به شکل زیر خواهد بود.

به این ترتیب، مشاهده میکنیم که میانگین متحرک رفتار نرمتری داشته و بیشتر روند کلی را نشان میدهد. توجه داشته باشید که در برخی نقاط، میانگین متحرک به نوسانهای کوتاهمدت نیز واکنش نشان داده است که میتوان با افزایش $$L$$ این مشکل را رفع کرد. حال اختلاف سری زمانی از میانگین متحرک را محاسبه میکنیم و نمایش میدهیم:
D2 = S2[-M2.size:] - M2
plt.plot(T2[-D2.size:], D2, lw=1, c='crimson')
plt.title('D2')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()که شکل زیر را خواهیم داشت.
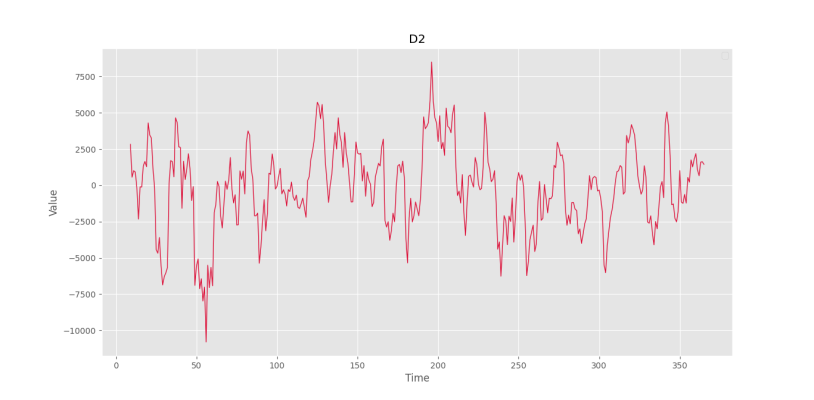
به این ترتیب، مشاهده میکنیم که تا حدود زیادی، روند حذف شده است. کاربرد میانگین متحرکها در حذف روند اینگونه بررسی میشود.
توجه داشته باشید که کم کردن میانگین متحرک از سری زمانی، در واقع معادل میانگینگیری از تفاضل سری زمانی با دادههای $$L$$ دوره قبل است:
$$ S_{t}-M_{t}=S_{t}-frac{1}{L} sum_{i=0}^{L-1} S_{t-i}=frac{1}{L} sum_{i=0}^{L-1}left(S_{t}-S_{t-i}right)=frac{1}{L} sum_{i=0}^{L-1} operatorname{Diff}(t, t-i) $$
به این ترتیب، میتوان مورد گفتهشده را اثبات کرد.
توجه داشته باشید که الزاماً مجبور نیستیم اختلاف بین میانگین متحرک و سری زمانی را محاسبه کنیم، بلکه میتوانیم نسبت آنها را نیز به سری زمانی بدون روند در نظر بگیریم، که در این صروت میتوانیم بنویسیم:
R2 = S2[-M2.size:] / M2
plt.plot(T2[-R2.size:], R2, lw=1, c='crimson')
plt.title('R2')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()و در خروجی به نمودار زیر برسیم.
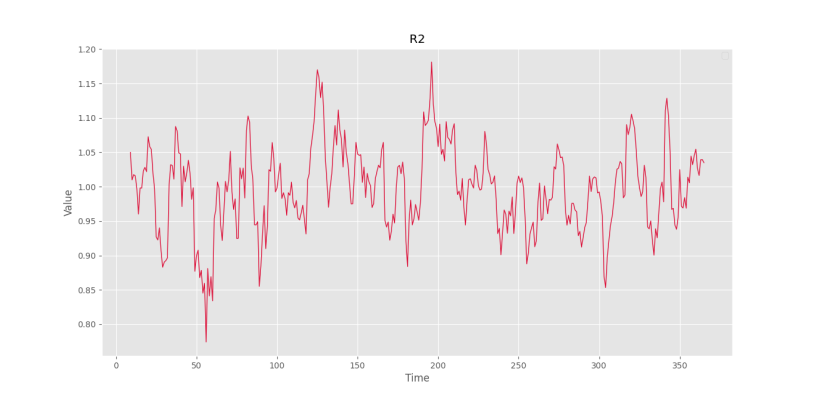
به این ترتیب، مشاهده میکنیم که سری زمانی حاصل، حول مقدار $$Y=1$$ نوسان میکند. برای دادههای مالی، استفاده از مدل ضربی و لگاریتم جمعی مناسبتر است.
مدلسازی روند با استفاده از رگرسیون
در این روش، برخلاف روشهای پیشین که بدون پارامتر (Non-Parametric) بودند، از مدلهایی استفاده میکنیم که دارای پارامتر هستند و با توجه به ویژگیهای هر مجموعه داده، تنظیم میشوند.
یک سری زمانی با رابطه زیر تولید میکنیم:
$$ Y _{t}=sin (10 times t)+t^{2}+I_{t} $$
که به شکل زیر داده را ایجاد و نمودار مورد نظر را رسم میکنیم:
T3 = np.linspace(start=-3, stop=+3, num=100)
S3 = np.sin(10 * T3) + np.power(T3, 2) + np.random.normal(loc=0, scale=0.1, size=(T3.size, ))
plt.plot(T3, S3, lw=1, c='crimson')
plt.title('S3')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()در خروجی نمودار زیر حاصل میشود.
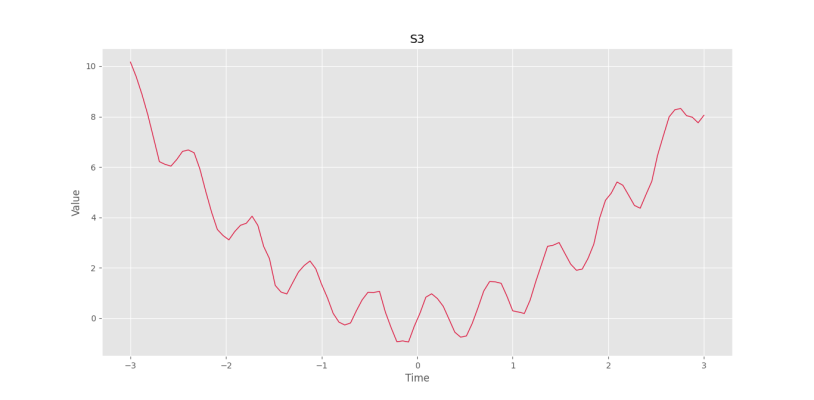
به این ترتیب، مشاهده میکنیم که داده دارای یک روند از نوع چندجملهای درجه دوم است. حال یک مجموعه داده درجه دوم ایجاد میکنیم:
t = T3.reshape((-1, 1))
t2 = np.power(t, 2)
X = np.hstack((t, t2))
Y = S3حال میتوانیم یک مدل خطی ایجاد و آن را با دادههای ایجادشده آموزش دهیم:
Model = lm.LinearRegression()
Model.fit(X, Y)اکنون پیشبینی مدل را برای مجموعه داده دریافت، و به همراه دادهها رسم میکنیم:
M3 = Model.predict(X)
plt.plot(T3, S3, lw=0.9, c='crimson', label='S3')
plt.plot(T3[-M3.size:], M3, lw=1, c='teal', label='M3')
plt.title('S3 + M3')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()که شکل زیر را خواهیم داشت.
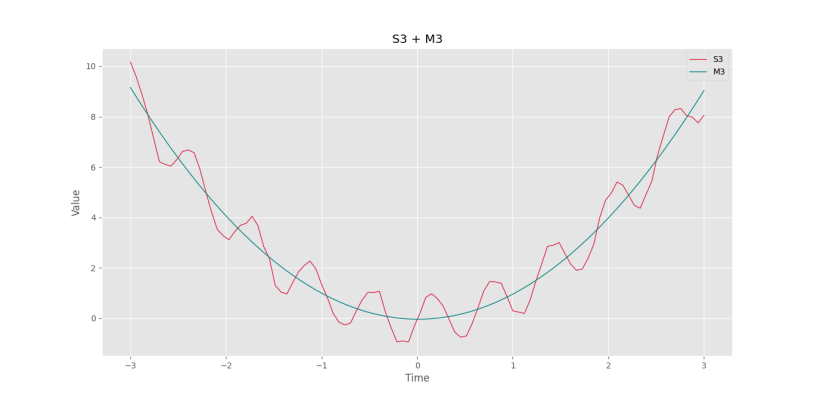
به این ترتیب، مشاهده میکنیم که روند به خوبی محاسبه میشود. حال میتوانیم اختلاف سری زمانی از روند را محاسبه کرده و رسم کنیم:
D3 = S3 - M3
plt.plot(T3, D3, lw=1, c='crimson')
plt.title('D3')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()که به نمودار زیر خواهیم رسید.
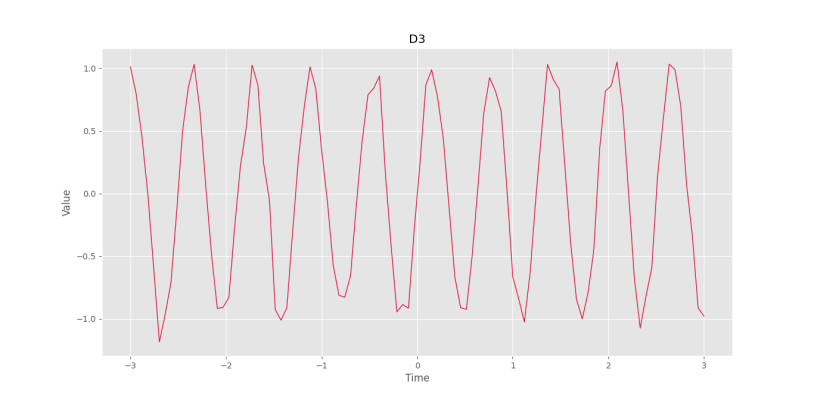
به این ترتیب، مشاهده میکنیم که سری زمانی حاصل، ایستا است.
توجه داشته باشید که نوع روند، باید با توجه به داده تعیین شود. برای مثال ممکن است روند به شکل هر کدام از موارد زیر باشد:
- خطی
- چندجملهای
- نمایی
توجه داشته باشید که روندهای چندجملهای به طور کلی قابلیت «تعمیمپذیری» (Generalization) خوبی ندارند.
در بعضی حالات نیز، میتوان داده را به نوعی «پیشپردازش» (Preprocessing) کرد و تغییر داد تا روند خطی شود، برای مثال در بازارهای مالی که به دلیل ماهیت نمایی، روند نیز رفتار نمایی دارد، اگر از قیمت، لگاریتم گرفته و بعد از آن روند خطی را محاسبه کنیم، مشاهده میکنیم که به خوبی بر روی دادهها قرار میگیرد.
فیلتر هودریک-پرِسکات
این فیلتر توسط Robert J. Hodrick و Edward C. Prescott رایج شده است که برای فیلتر کردن و تجزیه (Decomposition) سریهای زمانی استفاده میشود. فیلتر هودریک-پرِسکات بیشتر در اقتصاد کلان استفاده میشود و نقش «هموارسازی» (Smoothing) نیز دارد.
در این فیلتر، یک مسئله بهینهسازی به شکل زیر تعریف میشود:
$$min _{tau}left(sum_{t=1}^{T}left(y_{t}-tau_{t}right)^{2}+lambda sum_{t=2}^{T-1}left[left(tau_{t+1}-tau_{t}right)-left(tau_{t}-tau_{t-1}right)right]^{2}right)$$
به این ترتیب، اگر یک سری زمانی با طول $$T$$ داشته باشیم، به تعداد $$T$$ عدد پارامتر باید بهینهسازی شوند. بهینهسازی فوق باعث خواهد شد مقدار $$tau$$ به $$y$$ نزدیک شود و همزمان، این اتفاق با کمترین مشتق دوم رخ بدهد. به این ترتیب، سادهترین $$tau$$ محاسبه خواهد شد که به مقادیر واقعی نیز گرایش دارد.
برای استفاده از این فیلتر، قیمت ۲ سال اخیر رمز ارز Binance Coin را دریافت میکنیم و مقادیر Close را در یک آرایه جدا میکنیم:
DF4 = yf.download(tickers='BNB-USD', period='2y', interval='1d')
S4 = DF4['Close'].to_numpy()حال یک نمودار نیمهلگاریتمی (Semi-Logarithm) برای سری زمانی رسم میکنیم:
T4 = np.arange(start=0, stop=S4.size)
plt.semilogy(T4, S4, lw=1, c='crimson')
plt.title('S4')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()که شکل زیر را خواهیم داشت.
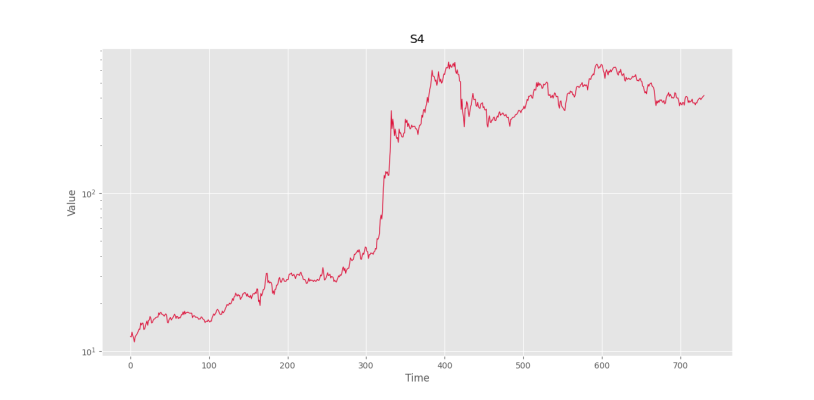
به این ترتیب، مشاهده میکنیم که داده دارای 3 فاز مختلف در روند میباشد، به همین دلیل یک روند خطی یا نمایی، نمیتواند به خوبی عمل کند. در این شرایط، فیلتر هودریک-پرِسکات مناسب خواهد بود.
برای استفاده از این فیلتر، به شکل زیر عمل میکنیم:
D4, M4 = hp.hpfilter(S4, lamb=10000)توجه داشته باشید که پارامتر lamb نشاندهنده میزان محدودیت مدل در ایجاد انحنا است و در صورتی که کم باشد، فیلتر به نوسانهای کوتاهمدت نیز واکنش خواهد داد و برعکس، اگر مقدار آن بسیار زیاد باشد، فیتلر تنها رفتار خطی از خود نشان خواهد داد.
حال نمودار مربوط به روند و سری زمانی را در کنار هم رسم میکنیم:
plt.semilogy(T4, S4, lw=0.9, c='crimson', label='S4')
plt.semilogy(T4[-M4.size:], M4, lw=1, c='teal', label='M4')
plt.title('S4 + M4')
plt.xlabel('Time')
plt.ylabel('Value')
plt.legend()
plt.show()که در خروجی، شکل زیر را خواهیم داشت.
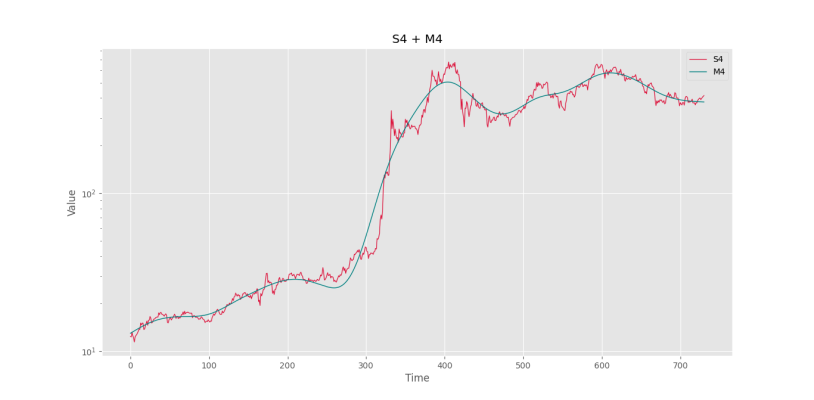
به این ترتیب، مشاهده میکنیم که فیلتر به خوبی توانسته روند را شناسایی کند. نکته مهمی که باید به آن توجه کرد، واکنش فیلتر به برخی نوسانهای کوتاهمدت در روزها مانند ۵۰، ۲۰۰ و ۵۲۰ است. برای رفع این مشکل، مقدار lamb را به ۳۰۰۰۰ افزایش میدهیم و خروجی به شکل زیر حاصل میشود.
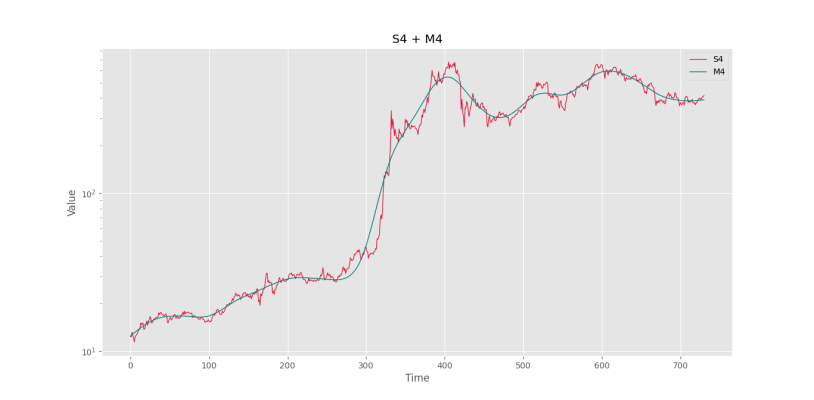
به این ترتیب، مشاهده میکنیم که روند خطیتر شده و تنها در نقاط مورد نیاز انحنا ایجاد کرده است. اگر مقدار lamb خیلی زیاد باشد، برای مثال در این مورد ۳۰۰۰۰۰، نتیجه به شکل زیر خواهد بود.
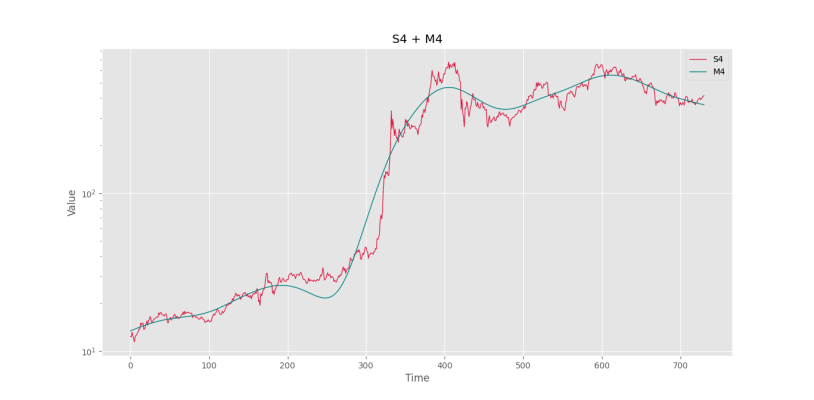
میبینیم که یک رفتار بسیار شدید در روز ۲۵۵ مشاهده میشود که دلیل آن، یک روند رشد شدید از روز ۳۰۰ تا ۴۰۰ است. به دلیل همین رشد، فیلتر مجبور است خود را با این روند تطبیق دهد، ولی در مقابل، شیب این بخش با شیب روش ۰ تا ۲۰۰ تفاوت زیادی دارد، به همین دلیل، این اختلاف در بازه ۲۰۰ تا ۲۹۰ فشرده میشود که دلیل این رفتار نامعمول است.
به همین دلیل، تنظیم صحیح $$lambda$$ بسیار مهم است. حال به ازای $$lambda = 30000$$ سری زمانی بدون روند را رسم میکنیم:
plt.plot(T4, D4, lw=1, c='crimson')
plt.title('D4')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()که شکل زیر را خواهیم داشت.
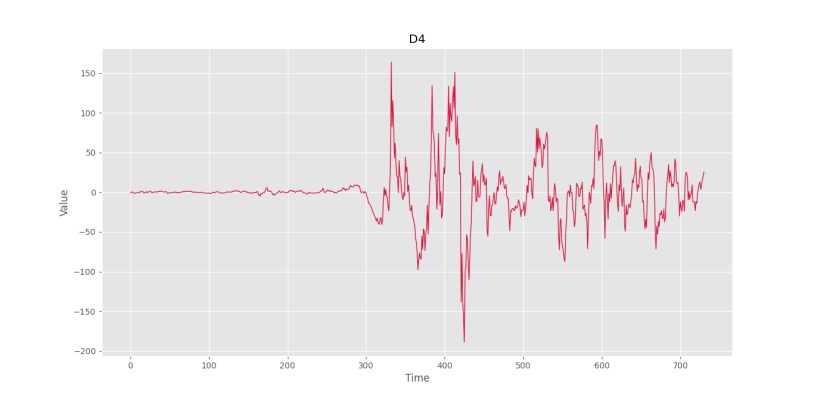
مشاهده میکنیم که در ۳۰۰ روز اول، واریانس سیگنال بسیار کوچک، ولی در باقی روزها واریانس بالایی وجود دارد. علت این مشکل، به روش محاسبه D4 برمیگردد که به صورت تفاضل محاسبه شده است. اگر از یک مدل ضربی استفاده کنیم و D4 را از نسبت سری زمانی اولیه به روند به دست آوریم، مشکل حل خواهد شد. به این منظور، به شکل زیر کد را تغییر میدهیم:
_, M4 = hp.hpfilter(S4, lamb=30000)
D4 = S4 / M4حال اگر رسم نمودار را تکرار کنیم، شکل زیر را خواهیم داشت.
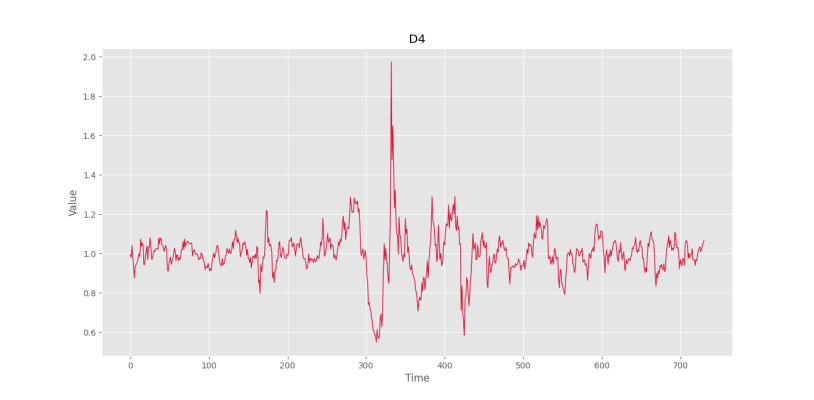
مشاهده میکنیم که در این حالت، واریانس سیگنال در ۳۰۰ روز اول با بقیه داده برابر است و میتواند کاربرد بهتری دارد.
با توجه به مطالب گفتهشده، مزایای فیلتر هودریک-پرِسکات بررسی شد. در کنار مزایای مهم این روش، برخی نقاط ضعف نیز وجود دارد، از جمله:
- این فیلتر برای تعیین مقدار روند در هر زمان، از دادههای بعدی نیز استفاده میکند. این موضوع در دادههای سری زمانی که به ترتیب زمان تولید میشوند، باعث مشکل میشود.
- رفتار این فیلتر در اواسط سری با انتهای آن متفاوت است.
- ممکن است با گذر زمان و اضافه شدن دادههای جدید، روند محاسبهشده توسط این فیلتر، تغییر کرده و اصلاح شود.
- تنظیم پارامتر Lambda ممکن است خیلی آسان نباشد.
جمعبندی حذف روند سری های زمانی در پایتون
در این مطلب، به ۴ روش حذف روند سری های زمانی پرداختیم و با دریافت یا تولید مجموعه دادهای، رفتار و نتایج هر کدام را نشان دادیم. برای مطالعه بیشتر، میتوان موارد زیر را بررسی کرد:
- چگونه میتوان مشکلات گفته شده برای فیتلر هودریک-پرِسکات را رفع کرد؟
- فیلتر هودریک-پرِسکات را با استفاده از Numpy و Scipy پیادهسازی کنید.
- چه معیاری میتواند میزان برازندگی یک روند استخراج شده از سری زمانی را نشان دهد؟
- در تحلیل تکنیکال بازارهای مالی، روند چگونه تشخیص داده میشود؟ چگونه میتوان فرآیند را کدنویسی کرد؟

