آموزش پیاده سازی بسط تیلور در پایتون — به زبان ساده | تم آف

بسط تیلور (سری تیلور | Taylor Series) روشی برای تخمین مقدار یک تابع با استفاده از مشتق مرتبه‌های مختلف آن تابع است. در این مقاله، آموزش پیاده‌سازی بسط تیلور در پایتون برای ۳ تابع پرکاربرد ارائه و نمودار حاصل از آن‌ها با نمودارهای واقعی مقایسه و مقدار خطا نیز محاسبه شده است.

بسط تیلور چیست؟

بسط تیلور روش هوشمندانه‌ای برای تخمین زدن هر تابع چند‌جمله‌ای با عبارت‌هایی به تعداد بی‌نهایت است. هر عبارت در چندجمله‌ای از مشتق‌های تابع در یک نقطه واحد برگرفته می‌شود.

فیلم آموزش محاسبات عددی – مرور و حل مساله در تم آف

کلیک کنید

براساس سری تیلور ، می‌توان تابع $$ f_{(x)} $$ را حول نقطه $$ x = a $$ به صورت زیر تخمین زد:

$$ f_{(x)} = f_{(a)} + frac{f’_{(a)}}{1!}(x-a)+ frac{f”_{(a)}}{2!}(x-a)^2 dots $$

می‌توان با استفاده از $$ sum $$ آن را به صورت زیر نوشت:

$$ f_{(x)} = sum_{n=0}^{infty}{frac{f^{(n)}_{(a)}}{n!}(x-a)^n} $$

براساس این رابطه، می‌توان برای توابع مختلف، تخمین چندجمله‌ای آن را پیدا کرد. برای مثال، بسط تیلور مربوط به برخی توابع پرکاربرد، حول $$ x = 0 $$ در زیر آورده شده است که به آن‌ها سری مک‌لورن نیز گفته می‌شود:

$$ e^x = sum_{n=0}^{infty}{frac{x^n}{n!}} = 1 + x + frac{x^2}{2!} dots  $$

$$ sin x = sum_{n=0}^{infty}{frac{(-1)^n}{(2n + 1)!}}x^{2n+1} =x – frac{x^3}{3!} + frac{x^5}{5!} dots  $$

$$ cos x = sum_{n=0}^{infty}{frac{(-1)^n}{(2n)!}}x^{2n} =1 – frac{x^2}{2!} + frac{x^4}{4!} dots  $$

باید توجه داشت که براساس همین روابط می‌توان فرمول اویلر را نیز اثبات کرد. این رابطه به صورت زیر است:

$$ e^{ix} = cosx + i space sinx $$

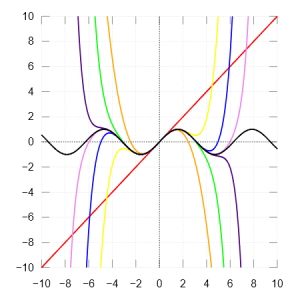
آموزش پیاده‌سازی بسط تیلور در پایتون

اکنون زمان آن فرا رسیده است تا وارد محیط برنامه نویسی پایتون شده و روابط ارائه شده در بخش قبل پیاده‌سازی شوند و در نهایت باید مقایسه با مقادیر واقعی صورت گیرد. مطابق معمول، اولین مرحله فراخوانی کتابخانه‌های مورد نیاز است.

فیلم آموزش محاسبات عددی در پایتون Python در تم آف

کلیک کنید

فراخوانی کتابخانه‌های مورد نیاز برای پیاده‌سازی بسط تیلور در پایتون

کتابخانه‌های مورد نیاز برای پیاده‌سازی بسط تیلور در پایتون شامل موارد زیرند:

1. ماژول math برای اعمال و توابع ریاضی کاربرد دارد.
2. کتابخانه numpy برای کار و عملیات روی آرایه‌ها استفاده می‌شود.
3. کتابخانه matplotlib برای رسم نمودار به کار می‌رود.

فیلم آموزش کتابخانه های NumPy و Matplotlib در پایتون در تم آف

کلیک کنید

کدهای مربوط به فراخوانی کتابخانه‌ها در ادامه آمده است:

import math as mt
import numpy as np
import matplotlib.pyplot as plt

ایجاد تابعی برای محاسبه $$ e^x $$ جهت پیاده‌سازی بسط تیلور در پایتون

اکنون لازم است تابعی تعریف شود که با دریافت مقدار $$x$$ و تعداد جمله‌ها در ورودی، مقدار $$ e^x $$ را در خروجی بازگرداند. تعریف (اعلان) این تابع در پایتون به صورت زیر انجام می‌شود:

def exponential(x:float, N:int=10):

باید توجه داشت که برای آرگومان ورودی دوم یعنی «N» مقدار پیش‌فرض نیز تعیین شده است تا در صورتی که ورودی دریافت نشد، مقدار آن را به طور پیش‌فرض برابر با 10 قرار داده شود.

فیلم آموزش محاسبات عددی در پایتون Python در تم آف

کلیک کنید

اکنون نیاز است متغیری تعریف شود تا مقدار خروجی را در خود ذخیره کند. این متغیر به تعداد «N» بار به‌روز‌رسانی خواهد شد. بنابراین کدهای مربوط به تعریف تابع «exponential» تا این مرحله به صورت زیر هستند:

def exponential(x:float, N:int=10):
    s = 0

اکنون باید یک حلقه تعریف شود تا نقش عملگر «$$ sum $$» را بازی کند. بنابراین تا اینجا تابع مورد نظر به صورت زیر خواهد بود:

def exponential(x:float, N:int=10):
    s = 0
    for n in range(N):

حال می‌توان رابطه مربوط به محاسبه $$ e^x $$ در داخل «$$ sum $$» را که پیش‌تر ارائه شد در داخل حلقه اضافه کرد. این رابطه به صورت $$ frac{x^n}{n!} $$ است:

def exponential(x:float, N:int=10):
    s = 0
    for n in range(N):
        s += x**n / mt.factorial(n)

به این صورت، پس از N بار به‌روزرسانی مقدار S، مقدار نهایی $$ e^x $$ حاصل خواهد شد و می‌توان آن را در خروجی بازگرداند:

def exponential(x:float, N:int=10):
    s = 0
    for n in range(N):
        s += x**n / mt.factorial(n)
    return s

اکنون تابع محاسبه $$ e^x $$ کامل شده است و می‌توان مقادیر مختلف را به آن ارجاع داد و خروجی را با مقادیر اصلی مقایسه کرد.

فیلم آموزش محاسبات عددی در پایتون Python در تم آف

کلیک کنید

آزمایش تابع $$ e^x $$ به وسیله ارجاع دادن مقادیر مختلف به آن و مقایسه خروجی با مقادیر اصلی

برای انجام این مقایسه، 100 نقطه از -2 تا +2 انتخاب می‌شوند و مقدار جواب تابع برای آن‌ها محاسبه می‌شود. بنابراین کدها به صورت زیر خواهند بود:

X = np.linspace(-2, +2, num=100)

Approximation = np.zeros(100)
for i,x in enumerate(X):
    Approximation[i] = exponential(x, 3)

Real = np.exp(X)

به این ترتیب، ابتدا مقادیر مختلف $$ x $$ تعریف می‌شوند؛ سپس مقدار تابع مربوطه تا 3 جمله محاسبه می‌شود. در نهایت نیز مقادیر واقعی محاسبه شده‌اند.

فیلم آموزش محاسبات عددی در پایتون Python در تم آف

کلیک کنید

رسم نمودار تابع $$ e^x $$ و مقادیر اصلی در کنار هم برای انجام مقایسه

اکنون بهتر است دو نمودار مربوط به هر یک از مقادیر اصلی و مقادیر تخمینی با بسط تیلور (تابع $$ e^x $$) را روی یک صفحه و در کنار هم رسم کرد تا بتوان مقایسه لازم را انجام داد. کدهای مربوط به رسم نمودار مربوطه در ادامه آمده‌اند:

plt.plot(X, Real, c='r', lw=1.2, ls='-', label='Real')
plt.plot(X, Approximation, c='b', lw=1.2, ls='--', label='Approximation (3)')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.show()

خروجی کدهای فوق به صورت زیر است:

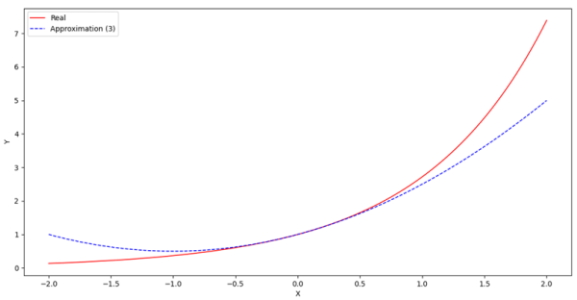
تخمین با 3 جمله، با اینکه در بازه $$ x = – 0.5 $$ تا $$ x = + 0.5 $$ از دقت مناسبی برخوردار است، اما در باقی نقاط دقت خوبی ندارد. با افزایش N از 3 به 10، به نتیجه زیر حاصل خواهد شد:

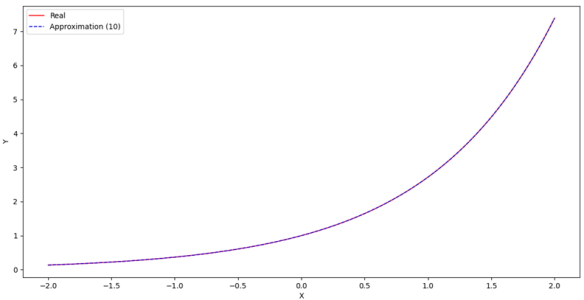
همان‌طور که مشاهده می‌شود، با افزایش N از 3 به 10، دقت بسیار خوبی به دست می‌آید. برای محاسبه میزان «خطای درصد میانگین مطلق» (Mean Absolute Percentage Error | MAPE)، می‌توان به صورت زیر عمل کرد. پیش از ارائه کدها ابتدا رابطه MAPE به عنوان یادآوری در ادامه آمده است:

$$MAPE(A,B) = 100 times sum{| frac{A_i – B_i}{A_i}|}$$

کدهای مربوط به پیاده‌سازی رابطه فوق برای محاسبه MAPE در پایتون به صورت زیر است:

MAPE = 100 * np.mean( np.abs( np.divide(Real - Approximation, Real) ) )

print(f'{MAPE = } %')

خروجی کدهای فوق به صورت زیر خواهد بود:

MAPE = 0.008044139334499392 %

همان‌طور که ملاحظه می‌شود، این خروجی عدد بسیار کوچکی است. می‌توان برای توابع سینوس و کسینوس نیز بسط تیلور را پیاده‌سازی کرد. این کار در ادامه انجام شده است.

فیلم آموزش محاسبات عددی در پایتون Python در تم آف

کلیک کنید

پیاده سازی بسط تیلور در پایتون برای تابع‌های سینوس و کسینوس

در این بخش کدهای مربوط به پیاده‌سازی بسط تیلور در پایتون برای تابع‌های سینوس و کسینوس ارائه شده‌اند. پیاده سازی بسط تیلور در پایتون برای تابع سینوس به صورت زیر است:

def sin(x:float, N:int=10):
    s = 0
    for n in range(N):
        s += (-1)**n * x**(2*n + 1) / mt.factorial(2*n + 1)
    return s

بنابراین، تابع مربوطه تعریف شده است و به درستی کار می‌کند. حالا باید نموداری را مشابه بخش‌های قبل برای مقایسه پیاده‌سازی تیلور با داده‌های واقعی رسم کرد. این نمودار در تصویر زیر نشان داده شده است:

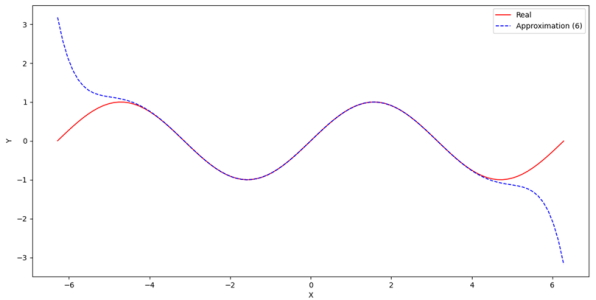
به این صورت، مشاهده می‌شود که با استفاده از 6 جمله، می‌توان بازه بین $$ x = -4 $$ تا $$ x = +4 $$ را به خوبی تخمین زد. به شیوه مشابه این پیاده‌سازی برای تابع کسینوس به صورت زیر است:

def cos(x:float, N:int=10):
    s = 0
    for n in range(N):
        s += (-1)**n * x**(2*n) / mt.factorial(2*n)
    return s

تصویر مقایسه خروجی تابع فوق با مقادیر اصلی در ادامه آمده است:

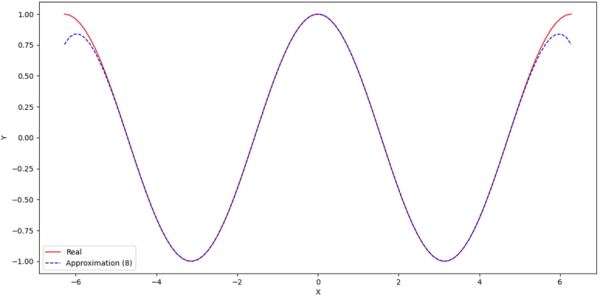
مقدار خطای درصد میانگین مطلق برای تابع کسینوس به صورت زیر است:

MAPE = 2.161881549770154 %

باید توجه داشت که برای محاسبه نسبت‌های مثلثاتی زاویه‌های مختلف، تنها باید مقدار نسبت‌ها را برای زاویه‌های $$ 0$$ تا $$ frac{pi}{2}$$ رادیان محاسبه کرد و مقدار این نسبت برای زاویه‌های دیگر می‌تواند با استفاده از روابط خاصی محاسبه شود.

اکنون در ادامه آموزش پیاده سازی بسط تیلور در پایتون به بهینه‌سازی توابع نوشته شده پرداخته شده است.

بهینه سازی توابع پیاده سازی سری تیلور در پایتون

به دلیل وجود حلقه و محاسبه عبارت‌های توان‌دار و فاکتوریل‌دار در توابع پیاده‌سازی شده در این مقاله، زمان اجرای آن‌ها ممکن است بسیار زیاد باشد. این مشکل می‌تواند با تعریف یک متغیر کمکی رفع شود. در این بخش به بهینه‌سازی توابع پیاده‌سازی سری تیلور در پایتون پرداخته شده است.

فیلم آموزش محاسبات عددی در پایتون Python در تم آف

کلیک کنید

در سری‌های پیاده‌سازی شده در این مقاله مشاهده شد که هر جمله، با جمله قبلی خود ارتباط دارد. برای مثال در مورد سری اول داریم:

$$ e^x = sum_{n=0}^{infty}{J_{(n)}}= sum_{n=0}^{infty}{frac{x^n}{n!}}= J_{(0)} + J_{(1)} + J_{(2)} dots = 1+x+ frac{x^2}{2!} dots$$

حال می‌توان بین jها رابطه زیر را مطرح کرد:

$$ J_{(n+1)} = frac{x^{n+1}}{(n+1)!} = frac{x}{n+1} times frac{x^n}{n!} = frac{x}{n+1} times J_{(n)} $$

بنابراین، می‌توان به جای محاسبه هر جمله از ابتدا، آن را از روی آخرین جمله ساخت:

def exponential2(x:float, N:int=10):
    s = 0
    j = 1
    for n in range(N):
        s += j
        j *= x/(n+1)
    return s

به این صورت، حجم محاسبات تابع بسیار کاهش پیدا می‌کند؛ به طوری که زمان محاسبه برای 10000 داده از 0.79 ثانیه به 0.59 ثانیه کاهش پیدا می‌کند. حال اگر به جای 10 جمله از 30 جمله استفاده شود، این زمان از 6.00 ثانیه به 1.71 ثانیه کاهش پیدا می‌کند که نشان دهنده کارآمد بودن این نوع پیاده‌سازی در جملات بالاتر است.

جمع‌بندی

در این مقاله بسط تیلور برای ۳ تابع پرکاربرد پیاده‌سازی شد، نمودار حاصل از آن‌ها با نمودارهای واقعی مقایسه و مقدار خطا نیز محاسبه شد.

فیلم مجموعه آموزش برنامه نویسی پایتون (Python) در تم آف

کلیک کنید

می‌توان برای مطالعه بیشتر، بسط تیلور را برای توابع دیگری نیز پیاده‌سازی و مراحل انجام شده را برای آن‌ها نیز تکرار کرد.