تقریب عدد پی در پایتون — راهنمای گام به گام

در آموزشهای پیشین مجله تم آف، با عدد پی (Π) و موضوعات جالب درباره آن آشنا شدیم. همچنین، تقریب عدد پی با روش سوزن بوفون و پیادهسازی آن را در متلب و پایتون را معرفی کردیم. در این آموزش، یک روش دیگر گام به گام تقریب عدد پی در پایتون را شرح میدهیم.

عدد پی و اهمیت آن
عدد پی در علوم مختلف از جمله ریاضیات، فیزیک، مهندسی و… اهمیت بالایی دارد. این عدد ارتباطدهنده محیط و مساحت یک دایره به شعاع آن است:
$$ large begin {align}
C& =2pi r \
S&=pi r^2
end {align} $$
بنابراین، این عدد بسیار مهم است و تخمین آن با دقت بالا، بسیار حائز اهمیت است.
روش تقریب عدد پی
برای تخمین عدد پی، آزمایشی طراحی میکنیم:
- یک مربع با ابعاد 2×2 در نظر میگیرم که مرکز این مربع، بر روی مرکز دستگاه مختصات دکارتی قرار میگیرد.
- یک دایره فرضی با شعاع 1 و با مرکز (0,0) نیز رسم میکنیم.
- به تعداد زیادی گوی کوچک را به صورت تصادفی روی مربع رها میکنیم و محل فرود را ثبت میکنیم.
- از نسبت گویهای درون به تعداد کل گویها، میتوانیم عدد پی را بیابیم.
فرض میکنیم به تعداد $$N$$ گوی رها کردهایم و به تعداد $$N_text{in}$$ گوی درون دایره فرود آمده است. براساس احتمالات میدانیم:
$$ large begin {align}
&frac {N_text {in}} {N}= frac {S_text{circle}}{S_text{square}} =frac {pi r^2}{(2r)^2} =frac {pi r^2}{4r^2}=frac {pi}{4}\
&Rightarrow pi = frac {4 N _ text{in}}{N}
end {align} $$
بنابراین، تنها با شمردن گویهای فرود آمده درون دایره، میتوانیم عدد پی را تخمین بزنیم.
تقریب عدد پی در پایتون
برای شبیهسازی وارد محیط پایتون میشویم و کتابخانههایی برای اعمال زیر فراخوانی میکنیم:
- برای کار با مختصات و تولید اعداد تصادفی
- برای رسم نمودار
import numpy as np
import matplotlib.pyplot as pltحال محیط آزمایش را طراحی میکنیم. ابتدا چهار گوشه مربع را تعیین و آن را رسم میکنیم:
Ps = np.array([[-1, -1], [-1, +1], [+1, +1], [+1, -1], [-1, -1]])
plt.plot(Ps[:, 0], Ps[:, 1], c='k', ls='-', lw=1.2)
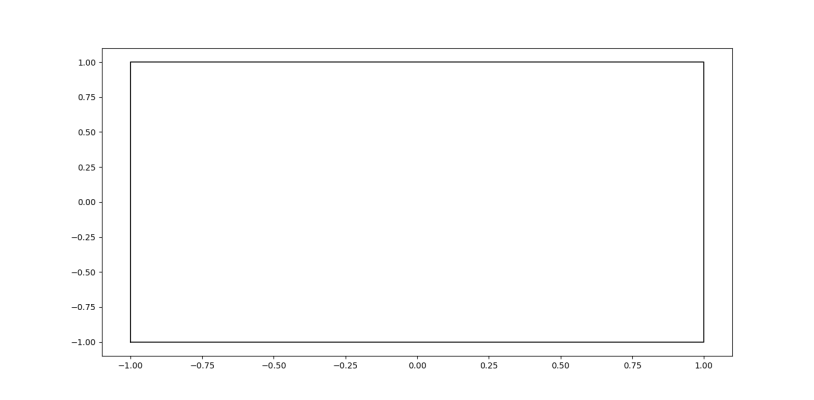
plt.show()توجه داشته باشید که برای نقطه (1- ,1-) دو بار تکرار شده است، زیرا میخواهیم یک مربع کامل رسم شود. در صورتی که این تکرار انجام نشود، ضلع پایین مربع، رسم نخواهد شد.
در خروجی این بخش کد، مربع مورد نظر به شکل زیر ایجاد میشود.
حال باید دایره مذکور را رسم کنیم. برای این کار میتوانیم تعداد زیادی زاویه از 0 تا 2π رادیان ایجاد کنیم و سینوس و کسینوس آنها را رسم کنیم:
Ps = np.array([[-1, -1], [-1, +1], [+1, +1], [+1, -1], [-1, -1]])
Rc = np.linspace(0, 2*np.pi, num=100)
Xc = np.cos(Rc)
Yc = np.sin(Rc)
plt.plot(Ps[:, 0], Ps[:, 1], c='k', ls='-', lw=1.2)
plt.plot(Xc, Yc, c='r', ls='--', lw=1.2)
plt.show()و در نهایت به نمودار گفته شده میرسیم.
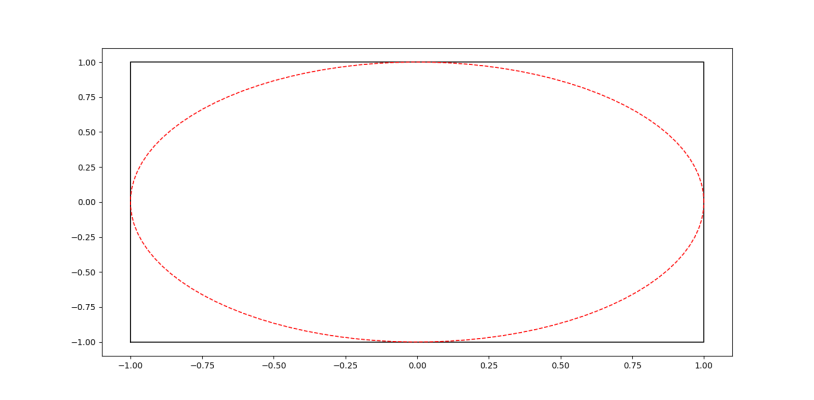
به این صورت هم مربع و هم دایره رسم شده است. حال نیاز است تعداد گویهای فرضی را مشخص و محل فرود آنها رو با صورت تصادفی انتخاب کنیم:
N = 5000
P = np.random.uniform(-1, +1, (N, 2))به این صورت، تعداد 5000 گوی انتخاب و محل فرود آنها به صورت تصادفی از 1- تا 1+ انتخاب میشود.
حال باید بررسی کنیم که کدام نقاط درون دایره و کدام بیرون دایره فرود آمدهاند.
میدانیم که نقاط مرزی دایره بهصورت زیر تعریف شدهاند:
$$ large P in { {(x,y)|x^2+y^2=1,x in mathbb {R},y in mathbb {R}} } $$
بنابراین، نقاط درون دایره به صورت زیر تعریف خواهد شد:
$$ large P_ text{in} in { {(x,y)|x^2+y^2 le 1,x in mathbb {R},y in mathbb {R}} }$$
پس محاسبه عبارت $$x^2+y^2$$ (فاصله اقلیدسی از مبدأ یا نُرم مرتبه دوم بردار مختصات) به ما در تعیین محل فرود گویها کمک خواهد کرد.
به این ترتیب، فاصله نقاط از مرکز دایره را بهصورت زیر محاسبه میکنیم:
R = np.hypot(P[:, 0], P[:, 1])توجه داشته باشید که از روشهای زیر نیز میتوان برای محاسبه فاصله از مرکز استفاده کرد:
R = (P[:, 0]**2 + P[:, 1]**2)**0.5
R = np.power(np.power(P[:, 0], 2) + np.power(P[:, 1], 2), 0.5)
R = np.linalg.norm(P, ord=2, axis=1)حال باید نقاط ایجادشده را به دو دسته In و Out تقسیم کنیم. برای این کار میتوانیم شاخص (Index) این نقاط را با استفاده از آرایه R تعیین کنیم:
In = P[R 1]توجه داشته باشید که خروجی عبارتهای $$Rle$$ و $$R>1$$ آرایهای به طول $$R$$ ولی از جنس بولی (Boolean) است.
حال که نقاط تقسیم شدند، برای داشتن تعداد نیز میتوانیم بنویسیم:
nIn = In.size
nOut = Out.sizeحال نقاط را وارد نمودار میکنیم و با توجه به اینکه داخل دایره قرار گرفتهاند یا بیرون آن، رنگهای مختلفی برای نشان دادن آنها به کار میبریم:
plt.plot(Ps[:, 0], Ps[:, 1], c='k', ls='-', lw=1.2)
plt.plot(Xc, Yc, c='r', ls='--', lw=1.4)
plt.scatter(In[:, 0], In[:, 1], s=7, c='b', alpha=0.8, label='In')
plt.scatter(Out[:, 0], Out[:, 1], s=7, c='g', alpha=0.8, label='Out')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend(loc='center', prop={'size': 15})
plt.show()در خروجی این بخش نمودار زیر را خواهیم داشت.
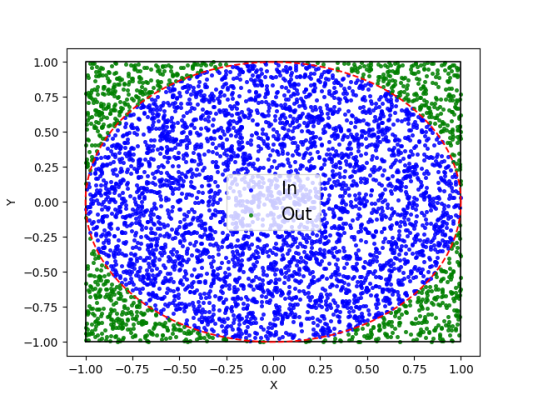
به این ترتیب، نقاط نیز انتخاب و جدا شدند.
حال تعداد گویهای داخل، بیرون و تخمین برای عدد پی را محاسبه میکنیم:
Pi = 2*nIn/N
print(f'Total Balls: {N}')
print(f'Balls Landed Inside: {nIn}')
print(f'Balls Landed Outside: {nOut}')
print(f'Pi Approximation: {Pi}')و به نتایج زیر میرسیم:
Total Balls: 5000 Balls Landed Inside: 7824 Balls Landed Outside: 2176 Pi Approximation: 3.1296
به این ترتیب مشاهده میکنیم که عدد بهدستآمده تا دو رقم اعشار درست است.
برای تخمین قدرمطلق درصد خطا نیز میتوانیم بنویسیم:
rPi = np.pi
E = rPi - Pi
APE = 100 * E / rPi
print(f'Error: {E}')
print(f'Absolute Percentage Error: {APE} %')که در خروجی خواهیم داشت:
Error: 0.011992653589793179 Absolute Percentage Error: 0.38173801992086953 %
به این ترتیب، درصد خطا حدود %0٫4 بوده که بسیار کم است.
حال اگر تعدا گویها را به 1 میلیون عدد برسانیم، نتایج زیر حاصل میشود:
Total Balls: 1000000 Balls Landed Inside: 1570464 Balls Landed Outside: 429536 Pi Approximation: 3.140928 Error: 0.0006646535897929517 Absolute Percentage Error: 0.021156580851864237 %
جمعبندی
به این ترتیب، در این مطلب با استفاده از قابلیتهای کتابخانههای Numpy و Matplotlib توانستیم عدد پی را با دقت بالایی تخمین بزنیم و نمودار حاصل را نمایش دهیم.
برای بررسیهای بیشتر میتوان:
- نمودار APE را بر حسب N را رسم کرد.
- نمودار زمان مورد نیاز برای رسیدن به APEهای مختلف را بررسی کرد.

