مدل خودهمبسته (Autoregressive) در پایتون — راهنمای گام به گام

در آموزشهای پیشین مجله تم آف، با پیادهسازی الگوریتم گرادیان کاهشی و روش نیوتون رافسون در پایتون آشنا شدیم. در این آموزش، مطالبی را درباره پیادهسازی مدل خودهمبسته در پایتون بیان میکنیم.

مدل خودهمبسته چیست؟
مدلهای خودهمبسته، از سادهترین و پرکاربردترین مدلها در پردازش سیگنال و تحلیل سریهای زمانی هستند. در این مدل، مقدار سیگنال در هر نقطه، به صورت ترکیبی خطی از $$p$$ نقطه قبل در نظر گرفته میشود.
برای مثال، اگر سری $$X$$ را بهصورت زیر داشته باشیم:
$$ large x _ 1 , x _ 2 , dots , x _{n-1} , x _ n $$
یک مدل خودهمبسته از مرتبه $$p$$ بهصورت زیر تعریف میشود:
$$ large
x_{t}=c+varphi_{1} x_{t-1}+varphi_{2} x_{t-2} +ldots+varphi_{p} x_{t-p}+varepsilon_{t}=c+sum_{i=1}^{p} varphi_{i} x_{t-i}+varepsilon_{t}
$$
در این رابطه، بردار $$varphi$$ ضرایب مربوط به نقاط قبلی بوده و $$c$$ عددی ثابت است. مقدار $$varepsilon_{t}$$ نیز نشاندهنده اندک خطای مدل از مقادیر مشاهدهشده است که توزیع نرمال با میانگین صفر دارد.
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
پیاده سازی مدل خودهمبسته در پایتون
حال که با مدل خودهمبسته آشنا شدیم، وارد محیط برنامهنویسی شده و کتابخانههای مورد نیاز را برای پیادهسازی مدل خودهمبسته در پایتون فراخوانی میکنیم:
import numpy as np
import scipy.stats as stt
import sklearn.metrics as met
import matplotlib.pyplot as plt
import sklearn.linear_model as lm
import sklearn.model_selection as msاین کتابخانهها بهترتیب برای موارد زیر کاربرد دارند:
- کار با آرایهها و محاسبات برداری
- محاسبه معیارهای آماری
- محاسبه معیارهای ارزیابی مدل
- رسم نمودار
- ایجاد و آموزش مدلهای خطی
- انتخاب مدل
حال میتوانیم Random State و Style را نیز تعیین کنیم:
np.random.seed(0)
plt.style.use('ggplot')برای بررسی مدل، نیاز به یک مجموعه داده داریم. از یک دوره تناوب تابع سینوسی بهعنوان داده استفاده میکنیم:
T = np.linspace(0, 2*np.pi, num=100)
X = np.sin(T)برای رسم نمودار مینویسیم:
plt.plot(T, X, marker='o', ms=3, label='Data')
plt.xlabel('t')
plt.ylabel('X(t)')
plt.legend()
plt.show()که نمودار زیر حاصل میشود.
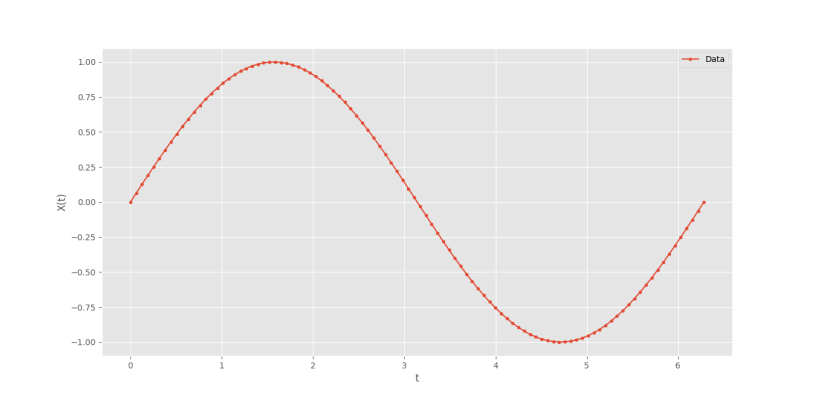
با افزودن اندکی نویز به مقادیر $$X$$ و کاهش ضخامت خط نمودار، نتیجه بهتر خواهد بود. بنابراین تولید داده را به شکل زیر تغییر میدهیم:
X = np.sin(T) + np.random.normal(0, 0.05, 100)سه ورودی آوردهشده برای تابع np.random.normal بهترتیب شامل میانگین توزیع، واریانس توزیع و تعداد نمونه است.
رسم نمودار را نیز به شکل زیر تغییر میدهیم:
plt.plot(T, X, marker='o', ms=3, lw=0.8, label='Data')که به نتیجه زیر میرسیم.
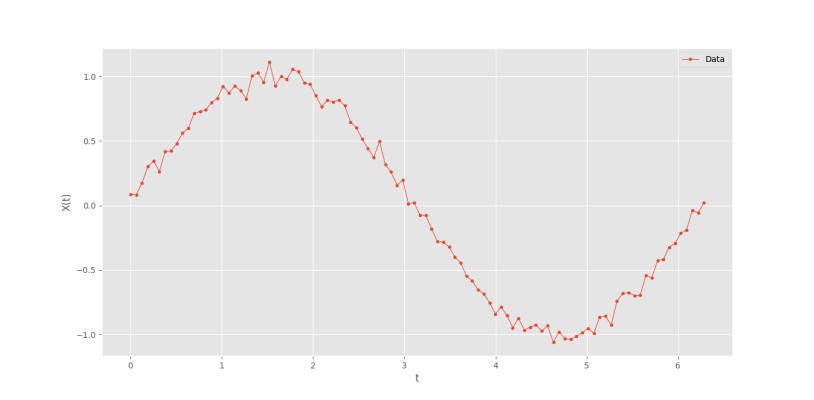
حال داده مورد نیاز آماده است.
برای ایجاد مدل خودهمبسته، نیاز است تا از خودهمبستگی (Autocorrelation) سیگنال مطمئن شویم. اولین و سادهترین راه، رسم Scatter Plot سیگنال نسبت به Lagهای متفاوت است.
اولین نمودار را نسبت به Lag=1 رسم میکنیم:
plt.scatter(X[:-1], X[1:], s=12)
plt.xlabel('X(t-1)')
plt.ylabel('X(t)')
plt.show()که نمودار زیر حاصل میشود.
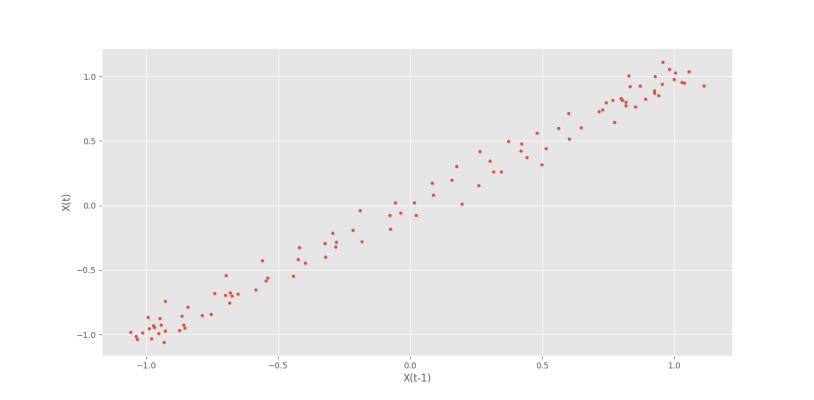
به این ترتیب، وجود ارتباطی خطی با Lag=1 تایید میشود.
با تکرار مراحل برای Lag=2 شکل زیر را خواهیم داشت.
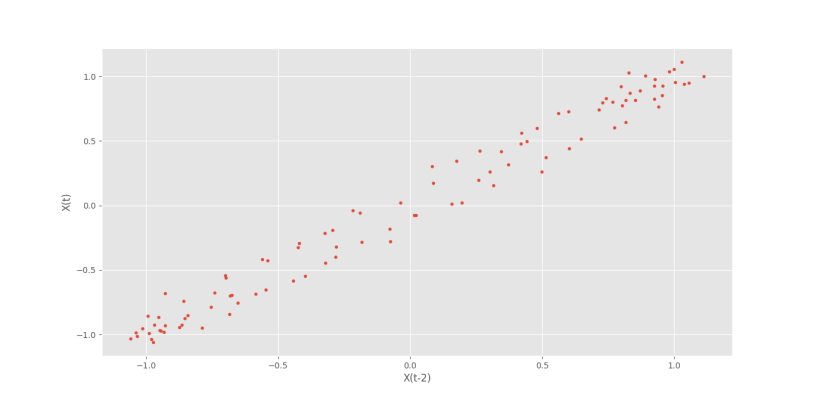
به این ترتیب، پخششدگی بیشتر میشود، ولی همچنان رابطه خطی با Lag=2 مشهود است.
حال اگر Lag=50 را بررسی کنیم، شکل زیر را خواهیم داشت.
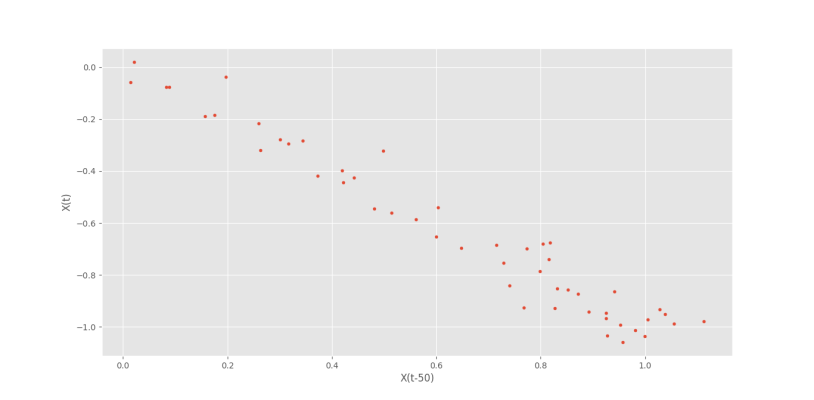
در این تصویر دو نکته به چشم میخورد:
- ضریب همبستگی عکس حالات قبلی است.
- تعداد نقاط کمتر است.
علت اتفاق اول، در ویژگی تابع سینوسی نهفته است. در یک تابع سینوسی، اگر دو نقطه بهصورت زیر داشته باشیم:
$$ large
begin{aligned}
&theta_{1}=alpha \
&theta_{2}=alpha+(2 k+1) pi
end{aligned}
$$
در این شرایط، این دو نقطه غیرهمفاز خواهند بود. در مجموعه داده ایجاد شده نیز فاصله یک دوره تناوب تقریباً به 100 بخش تقسیم شد که هر 50 نقطه معادل $$pi$$ خواهد بود، بنابراین، ارتباط با Lag=50 عکس خواهد بود.
علت اتفاق دوم نیز، از دست رفتن برخی دادهها بهدلیل نبودن Lag متناظر است. برای مثال، دادههای با شرایط $$t
حال میتوانیم مشاهدات نمودارها را به شکل آماری بررسی کرد و در یک نمودار نمایش داد.
برای این کار ضریب همبستگی پیرسون (Pearson Correlation Coefficient) را نسبت به Lagهای مختلف محاسبه میکنیم.
ابتدا Lagهای مورد نیاز را انتخاب و یک آرایه خالی برای ذخیرهسازی مقادیر خودهمبستگی ایجاد میکنیم:
Lags = np.arange(1 ,52, 1)
ACs = np.zeros(Lags.size)حال یک حلقه ایجاد میکنیم و تکتک خودهمبستگیها را محاسبه و به آرایه ACs اضافه میکنیم:
for i, l in enumerate(Lags):
ACs[i] = stt.pearsonr(X[:-l], X[+l:])توجه داشته باشید که تابع Scipy.stats.pearsonr دو خروجی ایجاد میکند که اولی مربوط به ضریب همبستگی است.
حال میتوانیم با یک Bar Plot خودهمبستگی سیگنال را نشان دهیم:
plt.bar(Lags, ACs, width=0.4)
plt.xlabel('Lag')
plt.ylabel('AC(Lag)')
plt.show()که نمودار زیر حاصل خواهد شد.
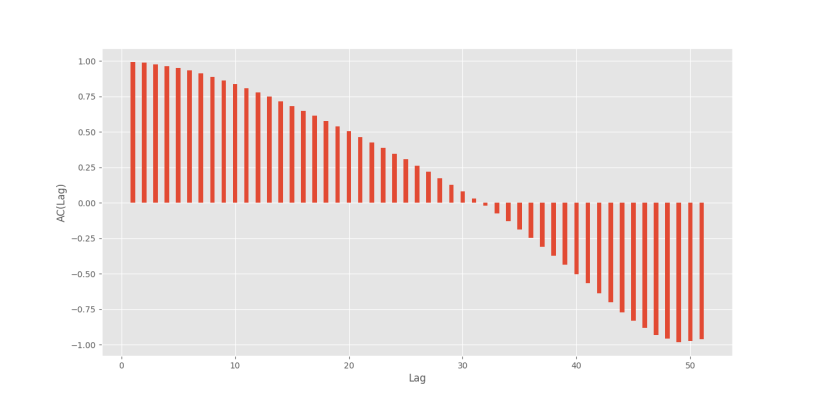
بنابراین، میتوان بهراحتی Lagهای مناسب را برای پیشبینی مشاهده کرد. توجه داشته باشید که مقدار همبستگی در Lag=0 برابر با 1 خواهد بود.
روش دیگر برای رسم نمودار خودهمبستگی، استفاده از تابع «plot_acf» موجود در کتابخانه «statsmodels» است.
حال که خودهمبستگی سیگنال اثبات شد، میتوان به تولید دادههای سری زمانی پرداخت. اگر یک مدل p=1 را در نظر بگیریم (پیشبینی تنها با توجه به یک نقطه قبلی)، مقدار سیگنال در Lag=1 بهعنوان ویژگی ورودی میتواند انتخاب شود و Lag=0 بهعنوان ویژگی هدف. برای مثال اگر سری بهصورت زیر باشد:
$$ large s_1,s_2, ldots ,s_{n-1},s_n $$
میتوان مجموعه داده را بهشکل زیر ایجاد کرد:
| $$Y$$ | $$X$$ |
| $$s_2$$ | $$s_1$$ |
| $$s_3$$ | $$s_2$$ |
| … | … |
| $$s_n$$ | $$s_{n-1}$$ |
به این ترتیب، اگر یک سیگنال با اندازه $$n$$ داشته باشیم، به تعداد $$n-p$$ داده خواهیم داشت.
برای پیادهسازی این بخش، یک تابع پیادهسازی میکنیم که در ورودی سری و $$p$$ را دریافت کرده و در خروجی مجموعه داده را برمیگرداند:
def CreateDataset(S:np.ndarray, nLag:int):
return X, Yحال در مرحله اول باید تعداد دادههای نهایی را تعیین کنیم. برای این کار ابتدا تعداد دادههای سیگنال را محاسبه میکنیم:
def CreateDataset(S:np.ndarray, nLag:int):
nD0 = S.size
nD = nD0 - nLag
return X, Yحال آرایههایی خالی برای ذخیرهسازی مقادیر $$X$$ و $$Y$$ ایجاد میکنیم:
def CreateDataset(S:np.ndarray, nLag:int):
nD0 = S.size
nD = nD0 - nLag
X = np.zeros((nD, nLag))
Y = np.zeros((nD, 1))
return X, Yتوجه داشته باشید که با افزایش تعداد Lag، تعداد ستونهای $$X$$ افزایش مییابد، ولی تعداد ستونهای $$Y$$ مستقل از Lag است.
حال یک حلقه ایجاد میکنیم و مقادیر را جایگذاری میکنیم:
def CreateDataset(S:np.ndarray, nLag:int):
nD0 = S.size
nD = nD0 - nLag
X = np.zeros((nD, nLag))
Y = np.zeros((nD, 1))
for i in range(nD):
X[i, :] = S[i:i + nLag]
Y[i, 0] = S[i + nLag]
return X, Yبه این ترتیب، تابع مورد نظر آماده است. برای تست کردن عملکرد صحیح تابع، یک سری ساده را به عنوان به آن وارد میکنیم تا نتایج را مشاهده کنیم:
S = np.arange(0, 7, 1)
X, Y = CreateDataset(S, 2)
print(X)
print(Y)که خواهیم داشت:
[[0. 1.] [1. 2.] [2. 3.] [3. 4.] [4. 5.]] [[2.] [3.] [4.] [5.] [6.]]
به این ترتیب، مشاهده میکنیم که تابع، عملکرد مورد نظر را از خود نشان میدهد.
حال میتوانیم سیگنال سینوسی ایجاد شده را وارد تابع کنیم:
x, y = CreateDataset(X, 2)حال مجموعه داده آماده شده است.
نیاز است تا مجموعه داده را به دو دسته آموزش و آزمایش تقسیم کنیم. برای این منظور، از بخش model_selection موجود در sklearn استفاده میکنیم:
Xtr, Xte, Ytr, Yte = ms.train_test_split(x, y, train_size=0.8, random_state=0)به این ترتیب مجموعه داده تقسیم میشود.
حال میتوانیم مدل خطی را ایجاد و بر روی دادهگان آموزش دهیم:
Model = lm.LinearRegression()
Model.fit(Xtr, Ytr)پس از اتمام آموزش، دقت مدل روی هر دو مجموعه داده را محاسبه و نمایش میدهیم:
R2tr = Model.score(Xtr, Ytr)
R2te = Model.score(Xte, Yte)
print(f'{R2tr = }')
print(f'{R2te = }')و خواهیم داشت:
R2tr = 0.9864373354377615 R2te = 0.9878940446792921
توجه داشته باشید که در کتابخانه statsmodels امکاناتی برای ایجاد مدلهای خودهمبسته نیز تعبیه شده است.
با توجه به بالا بودن دقتها و همچین نزدیک بودن آنها به هم، میتوان گفت مدل از دقت خوبی برخودار است و دچار بیشبرازش (Overfitting) نیز نشده است.
اگر واریانس نویز اضافه شده را از 0٫05 به 0٫15 تغییر دهیم، سیگنال و دقتهای زیر حاصل خواهد شد.
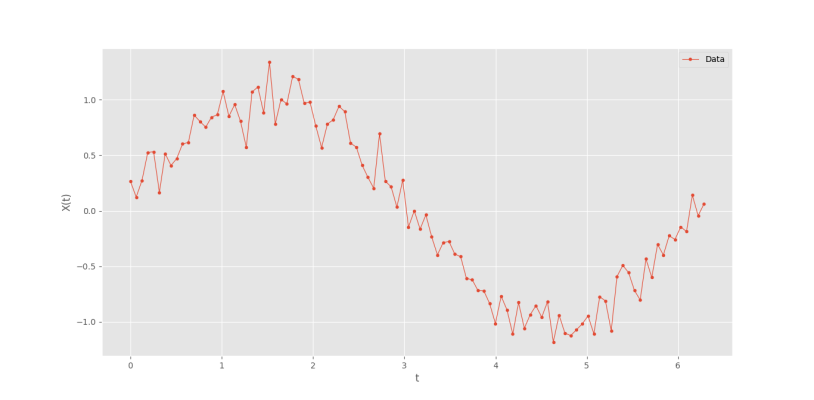
R2tr = 0.932242795568308 R2te = 0.9464468166093286
بنابراین، با افزایش نسبت نویز به سیگنال، دقت مدل در پیشبینی نیز کاهش مییابد.
افزایش nLag برای افزایش دقت در شرایطی که سیگنال رفتار پیچیدهای دارد کارآمد است، ولی در شرایطی که کم بودن دقت مدل ناشی از شدید بودن نویز باشد، افزایش nLag باعث Overfitting خواهد شد.
حال واریانس را به حالت قبلی برمیگردانیم و پارامترهای مدل را نمایش میدهیم:
Phi = Model.coef_
C = Model.intercept_
print(f'{Phi = }')
print(f'{C = }')که پارامترهای زیر ظاهر میشود:
Phi = [0.02306642, 0.9567478] C = -0.00382345
در بین ضرایب، عدد بزرگتر مربوط به Lag=1 است که منطقی است. ولی در مورد $$varphi _2$$ این نکته قابل بیان نیست. براساس نمودار خودهمبستگی، باید هر دو ضریب اعداد بزرگ و نزدیکی به 1 باشند. علت این اختلاف، در Partial Autocorrelation نهفته است. خودهمبستگی به دست آمده برای Lag=2، اندکی نیز از Lag=1 اثر پذیرفته است، بنابراین با کم کردن این مقدار از دورههای قبلی، مقدار خالص خودهمبستگی به دست میآید. با توجه به این اعداد، میتوان حدس زد که تغییر nLag از 2 به 1، کاهش چندانی در دقت مدل ایجاد نخواهد کرد.
عدد ثابت به دست آمده نیز مقداری بسیار کوچک نبست به دامنه سیگنال است و میتوان آن را نیز در نظر نگرفت. برای این مورد میتوان به شکل زیر عمل کرد:
Model = lm.LinearRegression(fit_intercept=False)حال پس از سادهسازیهای انجام شده، به دقت و پارامترهای زیر میرسیم:
R2tr = 0.9861532913089581 R2te = 0.9897503482050113 Phi = [0.99970675] C = 0.0
به این ترتیب مشاهده میکنیم که با تعداد پارامترهای کمتر، با دقتهای مشابهی رسیدیم. پس، انتخاب دقیق nLag یا همان p میتواند بسیار کمککننده باشد.
برای بررسیهای دقیقتر دقت مدل، سایر معیارهای پرکاربرد را نیز محاسبه و نمایش میدهیم:
MSE = 0.007608 RMSE = 0.087229 NRMSE = 0.040180 MAE = 0.072924 MAPE = 0.101543
از بین معیارهای محاسبه شده، NRMSE و MAPE و R2 بدون واحد (بُعد) هستند و به همین دلیل برای ارزیابی مدل مناسبتر هستند. برای مثال MAPE به سادگی بیان میکند که میانگین خطای نسبی 10% است.
برای دادههای آزمایش میتوان نمودار رگرسیون را نیز رسم کرد:
plt.scatter(Yte, Pte, s=12)
plt.plot([-1.2, +1.2], [-1.2, +1.2], ls='-', lw=1.2, c='k', label='y=x')
plt.plot([-1.2, +1.2], [-1.2*1.2, +1.2*1.2], ls='--', lw=0.8, c='b', label='y=1.2*x')
plt.plot([-1.2, +1.2], [-0.8*1.2, +0.8*1.2], ls='--', lw=0.8, c='b', label='y=0.8*x')
plt.title('Regression Plot')
plt.xlabel('Target Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.show()که نمودار زیر حاصل میشود.
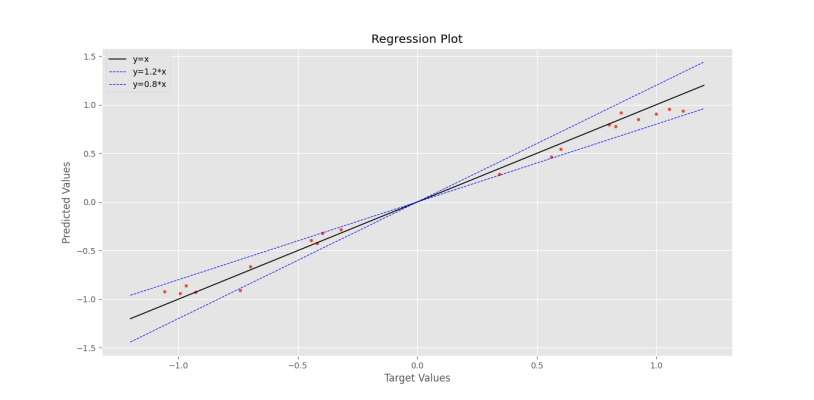
به این ترتیب نمودار رگرسیون نیز رسم شد.
در انتها برای تحلیل نویز سفید ادعا شده، بردار خطا را محاسبه و نمودار هیستوگرام آن را رسم میکنیم:
Pall = Model.predict(x)
E = y - Pall
plt.hist(E, bins=9)
plt.xlabel('y(Actual) - y(Predicted)')
plt.ylabel('N')
plt.show()و در خروجی به نمودار زیر میرسیم.
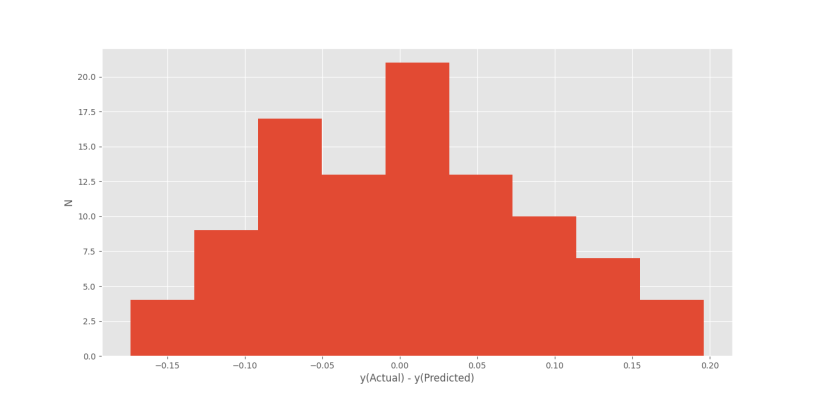
نمودار حاصل نسبتاً شبیه توزیع نرمال است. با افزایش دادهها از 100 به 500، وسیعتر کردن بازه زمانی از یک دوره به دو دوره و افزایش bins از 9 به 19، نمودار خطا به شکل زیر در میآید:
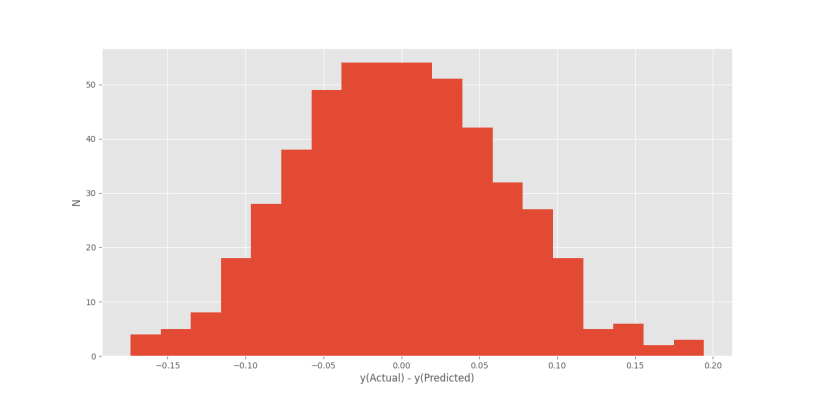
پیادهسازی مدل خودهمبسته در پایتون به این شکل انجام و به اتمام میرسد.
جمعبندی
در این آموزش، پیادهسازی مدل خودهمبسته در پایتون را بررسی کردیم. برای مطالعه بیشتر، میتوان موارد زیر را بررسی کرد:
- با کوچک کردن گام نمونهبرداری، پارامترها و دقت مدل چه تغییری میکند؟
- با افزایش تعداد دوره از یک به دو و دو به سه، پارامترها و دقت مدل چه تغییری میکند؟
- واریانس نمودار خطا چه ارتباطی با نویز اضافه شده به مجموعه داده دارد؟
- با پیچیده کردن دادهها (برای مثال استفاده از مجموع دو تابع سینوسی)، چه تغیراتی باید در پارامترهای مدلسازی ایجاد کنیم؟
- آیا نویز سفید موجود در سیگنال، قابل پیشبینی است؟ چه مقداری از این فرآیند تصادفی قابل پیشبینی است؟

