اپراتور سوبل در پایتون — راهنمای گام به گام

«اپراتور سوبل» (Sobel Operator) که به عنوان «فیلتر سوبل» (Sobel Filter) نیز شناخته میشود، محل شروع ایده شبکههای عصبی پیچشی (Convolutional Neural Network) است که امروزه از آن برای اهداف مختلفی مثل تشخیص چهره، تحلیل سری زمانی و… استفاده میشود. در این آموزش، به پیادهسازی اپراتور سوبل در پایتون میپردازیم.

اپراتور سوبل چیست؟
قبل از پرداختن به پسادهسازی سوبل در پایتون باید با آن آشنا شویم. این اپراتور یا فیلتر تقریبی از گرادیان (Gradient) تصویر را محاسبه میکند.
از آنجا که تصاویر دوبُعدی هستند، دو فیلتر سوبل در جهت افقی و عمودی به شکل زیر وجود دارد:
$$ large begin{aligned}
&F_{x}=left[begin{array}{ccc}
-1 & 0 & +1 \
-2 & 0 & +2 \
-1 & 0 & +1
end{array}right] \
&F_{y}=left[begin{array}{ccc}
+1 & +2 & +1 \
0 & 0 & 0 \
-1 & -2 & -1
end{array}right]
end{aligned} $$
این فیلتر روی تمامی موقعیتهای ممکن روی ماتریس پیکسلهای تصویر اعمال و تصویر خروجی حاصل میشود. به این عمل حرکت فیلتر روی ماتریس تصویر، پیچش (Convolution) گفته میشود.
از آنجا که این فیلتر تخمینی از گرادیان را محسابه میکند، به تغییر رنگ واکنش میدهد که از این ویژگی در بینایی ماشین (Computer Vision) برای تشخیص لبه (Edge Detection) استفاده میشود.
برای مثال فرض کنید تصویر اولیه زیر را داشته باشیم.

پس از اعمال سوبل عمودی روی آن، به تصویر زیر میرسیم.

بهخوبی مشاهده میشود که فیلتر نسبت به لبهها واکنش داده است. از طرفی برخی لبهها که عمود بر جهت فیلتر هستند، تقریباً حذف شدهاند.
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
پیاده سازی اپراتور سوبل در پایتون
ابتدا کتابخانههای مورد نیاز را فراخوانی میکنیم:
import cv2 as cv
import numpy as np
import scipy.ndimage as ndimg
import matplotlib.pyplot as pltاین کتابخانهها بهترتیب برای کار با تصاویر، کار با آرایهها، محاسبات روی تصاویر و رسم نمودار و تصاویر استفاده خواهند شد.
یک تصویر انتخاب و در کنار فایل برنامه قرار میدهیم. سپس آن را به شکل زیر در محیط برنامهنویسی میخوانیم:
Path = 'Picture_1.jpg'
Image = cv.imread(Path, 0)ورودی دوم برای تابع imread تعیین میکند تا تصویر به صورت سیاه سفید خوانده شود.
حال تصویر اولیه را با استفاده از کتابخانه Matplotlib رسم میکنیم:
plt.imshow(Image, cmap='gray')
plt.title('Original Image')
plt.show()و در خروجی تصویر زیر حاصل میشود.

به این ترتیب، تصویر مورد نظر به درست فراخوانی و رسم شد.
حال فیلتر سوبل را تعریف میکنیم:
Fx = np.array([[-1, 0, +1],
[-2, 0, +2],
[-1, 0, +1]])اکنون میتوانیم ابعاد تصویر خروجی را محاسبه کنیم:
h0, w0 = Image.shape
s1, s2 = Fx.shape
h, w = h0-s1+1, w0-s2+1توجه داشته باشید که با اعمال یک فیلتر ۳×۳ بر روی تصویر، اندازه هر بُعد تصویر ۲ عدد کاهش مییابد؛ به همین دلیل عدد ۱+ به هر دو بعد اضافه شده است.
حال آرایهای خالی برای تصویر نهایی ایجاد میکنیم:
Gx = np.zeros((h, w))اکنون میتوانیم دو حلقه تو در تو برای هر بعد از تصویر ایجاد کنیم:
for i in range(h):
for j in range(w):در این بخش، عمل Convolution انجام میشود:
for i in range(h):
for j in range(w):
Gx[i, j] = np.multiply(Image[i:i+s1, j:j+s2], Fx).sum()به این ترتیب، ماتریس فیلتر به بخش انتخاب شده از تصویر ضرب و مجموع ماتریس نهایی بهعنوان مقدار پیکسل در نقطه مورد نظر استفاده میشود.
تصویر حاصل را به شکل زیر رسم میکنیم:
plt.imshow(Gx, cmap='gray')
plt.title('Gx')
plt.show()که نتیجه آن بهصورت زیر خواهد بود.

میبینیم که حاشیهها بهخوبی تشخیص داده شده است. اگر برای فیلتر $$F_y$$ فرایند را تکرار کنیم، تصویر زیر حاصل میشود.
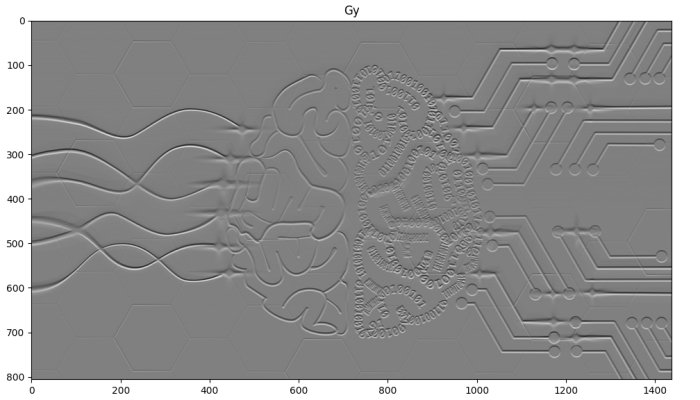
به این ترتیب، برخی خطوط افقی که در فیلتر قبلی تشخص داده نشده بودند، مشاهده میشوند.
توجه داشته باشید که میتوان فیلترهای گفتهشده را میتوان به شکل زیر نیز محاسبه کرد:
Sobel = ndimg.sobel(Image)حال تابع Filter را برای استفادههای بعدی بهشکل زیر تعریف میکنیم:
def Filter(Image:np.ndarray, F:np.ndarray):
h0, w0 = Image.shape
s1, s2 = F.shape
h, w = h0-s1+1, w0-s2+1
G = np.zeros((h, w))
for i in range(h):
for j in range(w):
G[i, j] = np.multiply(Image[i:i+s1, j:j+s2], F).sum()
return Gبه این ترتیب، میتوانیم هر فیلتر را روی تصاویر به راحتی اعمال کنیم. برای مثال یک فیلتر به شکل زیر طراحی میکنیم:
$$ large F_{1}=left[begin{array}{ccc}
0 & -1 & 0 \
-1 & +4 & -1 \
0 & -1 & 0
end{array}right] $$
حال فیلتر را وارد محیط کرده و روی تصویر اعمال میکنیم:
F1 = np.array([[0, -1, 0],
[-1, +4, -1],
[0, -1, 0]])
Output1 = Filter(Image, F1)در نتیجه، تصویر خروجی زیر را خواهیم داشت.
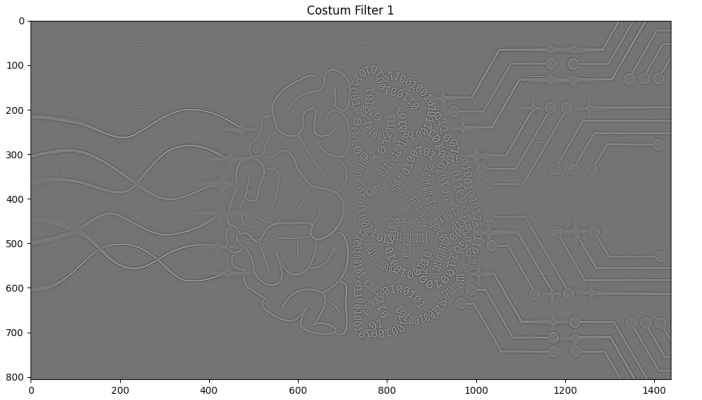
مشاهده میکنیم که رفتار شدیدی در خروجی این فیلتر مشاهده نمیشود. در مقابل، تمامی حاشیهها بهخوبی تشخیص داده شدهاند.
حال اگر فیلتر دیگری به شکل زیر تعریف شود:
$$ large F_{2}=left[begin{array}{ccc}
-0.5 & -1 & -0.5 \
-1 & +6 & -1 \
-0.5 & -1 & -0.5
end{array}right] $$
و فرایند را برای آن نیز تکرار کنیم، تصویر خروجی به شکل زیر خواهد بود.
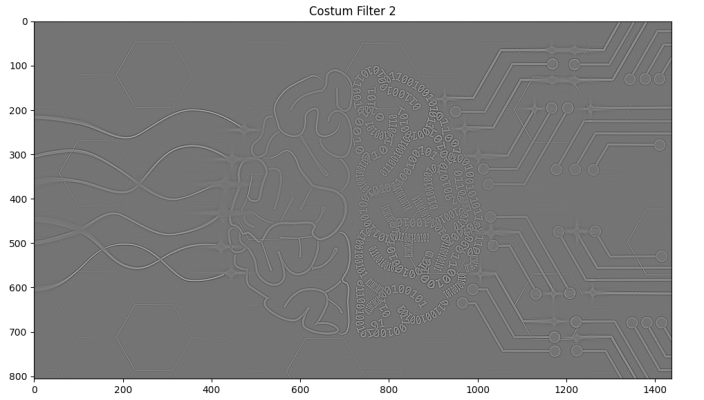
با اینکه تصویر حاصل تقریباً مشابه فیلتر قبلی است، اما اندکی بهبود رفتار نسبت به تغییرات در آن مشاهده میشود.
میتوان فیلترهایی نیز برای تشخیص حاشیههای مایل طراحی کرد، برا مثال اگر فیلتری به شکل زیر تعریف شود:
$$ large F_{3}=left[begin{array}{ccc}
-1 & 0 & 0 \
0 & 0 & 0 \
0 & 0 & +1
end{array}right] $$
شکل زیر نشان میدهد که میتوانیم خطوط مایل نزدیک به ۴۵ و ۲۲۵ درجه را بهخوبی تشخیص دهیم.
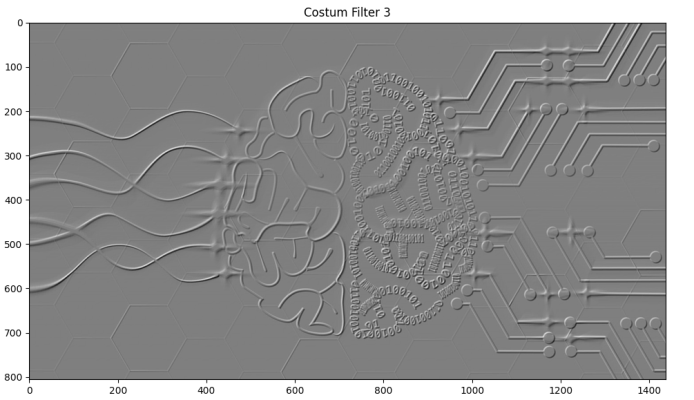
به این ترتیب، مشاهده میکنیم که حاشیههای با زاویه نزدیک به ۴۵ و ۳۱۵ بیشتر مورد توجه قرار میگیرند.
علاوه بر کار تشخیص حاشیه، میتوانیم از این فیلترها برای محو کردن تصویر نیز استفاده کنیم:
$$ large F_{4}=left[begin{array}{ccc}
frac{1}{9} & frac{1}{9} & frac{1}{9} \
frac{1}{9} & frac{1}{9} & frac{1}{9} \
frac{1}{9} & frac{1}{9} & frac{1}{9}
end{array}right] $$
با اعمال این فیلتر نیز نتیجه زیر حاصل میشود.

به این ترتیب، اندکی محوشدگی در تصویر ایجاد میشود. میتوان فیلتر محو کردن را در اندازه ۵×۵ استفاده کرد و به شکل زیر محوشدگی بیشتری ایجاد کرد.

به این ترتیب، اندازه فیلتر نیز در نتایج اثرگذار است.
مشاهده کردیم که فیلترها میتوانند اطلاعات ارزشمندی از تصاویر استخراج کنند. از این رو، توجه به فیلترها جلب شد و در نهایت منجر به معماری خاصی از شبکههای عصبی به نام شبکههای عصبی پیچشی (Convolutional Neural Network) شد. در این شبکهها، تعداد زیادی فیلتر بر روی تصویر ورودی اعمال میشود و نتایج حاصل باز هم میتواند وارد فیلترهای جدیدی شود که در نهایت منجر به استخراج ویژگیهای (Feature Extraction) مهم برای پیشبینی میشود.
جمعبندی سوبل در پایتون
در این مطلب با سوبل در پایتون و فیلترها در بینایی ماشین آشنا شدیم و اهمیت و کارایی آنها مورد بررسی قرار دادیم.
برای مطالعه بیشتر، میتوان موارد زیر را بررسی کرد:
- تغییر وزنها در فیلترهای آورده شده، منجر به چه تغییراتی در تصاویر خروجی خواهد شد؟
- شبکههای عصبی پیچشی، چگونه فیلترهای خود را انتخاب میکند؟
- در طول انجام عمل پیچش، ممکن است مقدار پیکسلی بسیار بزرگ شود، این موضوع چه مشکلاتی میتواند ایجاد کند؟ راهحل آن چیست؟
- آیا راهی برای افزایش سرعت تابع نوشتهشده وجود دارد؟
- فیلترهای آوردهشده را چگونه میتوان بر روی تصاویر رنگی اعمال کرد؟

