پیاده سازی یادگیری Q عمیق یا Deep Q-Learning در پایتون – راهنمای گام به گام

در مطلب گذشته به پیاده‌سازی یادگیری Q یا Q-Learning در پایتون پرداختیم. اگر با این مبحث آشنا نیستید، توصیه می‌کنیم ابتدا مطلب پیاده سازی الگوریتم Q-Learning در پایتون – راهنمای گام به گام را مطالعه کنید. در این مطلب قصد داریم نحوه پیاده سازی Deep Q Learning را در پایتون یاد بگیریم و کدنویسی آن را به طور کامل بررسی کنیم.

در مطلب گذشته متوجه شدیم که اگر به تعداد «عمل» (Action) و m «شرایط» (State) داشته باشیم، Q-Table نهایی به شکل $$mtimes n$$ خواهد بود. حال اگر تعداد اعمال یا شرایط خیلی زیاد باشد، این شیوه از تخمین مقادیر Q (Quality یا ارزش) بهینه نخواهد بود. برای مثال اگر بخواهیم برای یک ماشین خودران که می‌تواند هزاران حالت از محیط را مشاهده کند و ده‌ها تصمیم بگیرد، به این شیوه عمل کنیم، به مشکل خواهیم خورد.

یکی از راه حل‌های این مشکل، استفاده از شبکه‌های عصبی مصنوعی (Artificial Neural Network یا ANN) است. شبکه‌های عصبی عمیق (Deep Neural Network یا DNN) در صورتی که به درستی آموزش ببیند، می‌توان نتایج آن را تعمیم داد. در این شرایط به جای ذخیره مقادیر Q در یک جدول، می‌توانیم پیش‌بینی مدل برای Q را استفاده کنیم.

در مطلب گذشته، به شکل زیر یک جدولی ایجاد کردیم که با دریافت شرایط و عمل، Q آن را برمی‌گرداند:

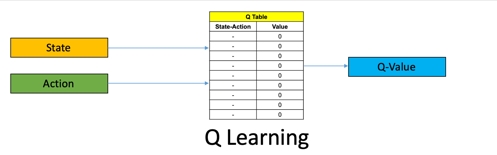
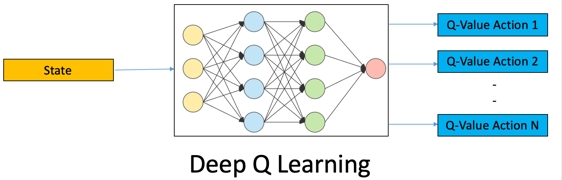
اما برای Deep Q-Learning به شکل زیر عمل می‌کنیم:

دانلود کد آماده برای پیاده سازی Deep Q Learning

با توجه به پیچیدگی کدهای مربوط به پیاده سازی Deep Q Learning، کدهای آماده این مطلب در فایل زیر قابل دانلود است. اما از آنجا که هدف این مطلب، آموزش پیاده سازی Deep Q Learning در پایتون است،‌ بخش‌های مختلف این کدها توضیح داده شده است.

• برای دانلود کد آماده در پیاده سازی Deep Q Learning + اینجا کلیک کنید.

پیاده سازی Deep Q Learning در پایتون

در این روش یک شبکه عصبی عمیق ایجاد می‌شود و به نحوی آموزش می‌بیند که با دریافت شرایط، Q مربوط به هر عمل را در خروجی برگرداند.

این شبکه عصبی باید به اندازه ابعاد شرایط ورودی داشته باشید و به تعداد اعمال خروجی داشته باشد. به این ترتیب حتی در صورتی که شرایط پیوسته نیز باشد، باز هم می‌توان از شبکه عصبی کمک گرفت.

در کنار شباهت‌های زیادی که بین ­Q-Learning و Deep Q-Learning وجود دارد، تفاوت‌های بسیار مهم نیز بین این دو روش وجود دارد که در ادامه به آن‌ها پرداخته می‌شود:

در روش Q-Learning برای یادگیری مقادیر Q از فرمول زیر استفاده می‌کردیم:

$$Q(s, a)^{text {new }} leftarrow Q(s, a)^{text {old }}+alphaleft[r+gamma max _{a^{prime}} Qleft(s^{prime}, a^{prime}right)^{text {old }}-Q(s, a)^{text {old }}right]$$

با به‌روزرسانی این مقادیر، یادگیری عامل به اتمام می‌رسید، اما در Deep Q-Learning پس از به‌روزرسانی مقادیر Q، باید مدل عمیق نیز بر روی این داده‌ها آموزش ببیند.

در روش Q-Learning اغلب مقادیر کوچک برای نرخ یادگیری (Learning Rate) $$alpha$$ مناسب است، اما در Deep Q-Learning اغلب مقادیر بالای $$alpha$$ مناسب است. در اغلب موارد مقدار نرخ یادگیری برابر با 1 در نظر گرفته می‌شود که در این صورت رابطه به‌روزرسانی مقادیر Q به شکل زیر ساده می‌شود:

$$Q(s, a)^{n e w} leftarrow r+gamma max _{a^{prime}} Qleft(s^{prime}, a^{prime}right)^{text {old }}$$

نکات زیر را نیز باید در زمان پیاده سازی Deep Q Learning در نظر داشته باشید:‌

• در روش Q-Learning تمامی مقادیر Q به صورت ذخیره شده آماده بودند، اما در Deep Q-Learning باید شرایط فعلی را وارد مدل کنیم تا در خروجی مقادیر Q را تولید کند.
• آموزش عامل در Deep Q-Learning زمان‌برتر از Q-Learning است.
• در آموزش Deep Q-Network، با به‌روزرسانی وزن‌ها نسبت به یک داده (شامل شرایط اولیه، عمل انجام شده، پاداش دریافتی و شرایط بعدی)، مقادیر Q برای سایر شرایط نیز تغییر می‌کند، درحالیکه در Q-Table این اتفاق رخ نمی‌داد. این اتفاق باعث می‌شود که مدل مرتباً یک مقداری از Q را تعقیب کند و هرگز به آن نرسد.
  این اتفاق یک مشکل برای آموزش مدل است که در ادامه مطلب به روش مقابله با آن خواهیم پرداخت. اگر محیط را یک تور در نظر بگیریم، هر گره از آن را یک شرایط در نظر بگیریم و این تور را از محلی آویزان کنیم، ارتفاع آن برابر با Qها خواهد بود. اگر پس از یادگیری مدل، Q یکی از این شرایط افزایش پیدا کند (ارتفاع آن زیاد شود)، نقاط همسایه نیز به سمت بالا حرکت خواهند کرد. در این شرایط عبارت می‌تواند تحت یک فرآیند خودتنظیمی مثبت (Positive Feedback) مرتباً افزایش می‌یابد و باعث افزایش $$Q(s, a)^{n e w}$$ و برعکس آن نیز رخ می‌دهد. در این شرایط مقادیر Q واگرا خواهد شد.
• در Q-Learning مقادیر اپسیلون یا $$epsilon$$ را به صورت خطی در طول اپیزودها (Episode) کاهش می‌دادیم، اما برای Deep Q-Learning اغلب دو فاز وجود دارد، در فاز اول کاهش (Decay) اپسیلون را به صورت خطی یا نمایی شاهد هستیم اما در فاز دوم مقادیر اپسیلون ثابت شده و برابر با مقدار نهایی می‌شود.
• در ­Q-Learning چون مدلی برای آموزش وجود ندارد، از الگوریتم‌های بهینه‌ساز (Optimizer) استفاده نمی‌شود، اما برای آموزش Deep Q-Network از الگوریتم‌های بهینه‌ساز استفاده می‌کنیم، بنابراین باید ورودی‌ها و خروجی‌های مدل باید در بازه مشخصی (اغلب در بازه $$[-1,+1]$$ یا $$[0,+1]$$ ) قرار گیرند یا میانگین و واریانس آن‌ها به ترتیب برابر با 0 و 1 باشد. به این دلیل، باید مقادیر State و Q در صورت نیاز تغییر مقیاس (Scaling) داده شوند.

حال کدنویسی را شروع می‌کنیم. کد نهایی حاصل، یک کلاس (Class) به نام WORLD خواهد بود که به شکل زیر استفاده خواهد شد:

World = WORLD()

World.CreateModel()
World.CompileModel()
World.ModelSummary()

World.PlotEpsilons()
World.PlotState2Reward()

World.Train()

World.SaveModel()

World.PlotActionLog()
World.PlotEpisodeLog()
World.PlotModelPrediction('Model Prediction For Q Against Real Values (Final)')

for _ in range(10):
    World.Test()

حال برای شروع، کتابخانه‌های مورد نیاز را فراخوانی می‌کنیم:

import os as os
import numpy as np
import typing as typ
import random as ran
import colorama as col
import tensorflow as tf
import collections as co
import matplotlib.pyplot as plt
import tensorflow.keras.layers as lay
import tensorflow.keras.models as mod
import tensorflow.keras.losses as los
import tensorflow.keras.optimizers as opt
import tensorflow.keras.activations as act
import tensorflow.keras.initializers as ini

کاربرد این کتابخانه‌هادر پیاده سازی Deep Q Learning به ترتیب زیر است:

• ماژول os برای استفاده از امکانات سیستم عامل (Operating System) است.
• کتابخانه Numpy برای محاسبات برداری، ذخیره داده و برخی تنظیمات برنامه استفاده خواهد شد.
• ماژول typing برای تعیین جنس متغیرها استفاده خواهد شد. تعیین جنس متغیرها برای استفاده‌های بعدی و افزایش خوانایی کد بسیار مهم است.
• ماژول random برای تولید اعداد تصادفی استفاده می‌شود. هرچند که برخی کتابخانه‌ها نیز خود برای تولید اعداد تصادفی امکاناتی دارند.
• کتابخانه Colorama برای نوشتن متون رنگی کاربرد دارد. رنگی کردن نوشته‌ها در شرایط که مقدار زیادی متن در خروجی کد ایجاد می‌شود، می‌تواند مفید باشد.
• کتابخانه Tensorflow برای ایجاد و آموزش مدل عمیق استفاده خواهد شد.
• ماژول collections انواعی از ساختمان‌های داده (Data Structure) مختلف را دارد که از نوع Deque برای ایجاد حافظه برای مدل استفاده خواهد شد.
• کتابخانه Matplotlib نیز برای رسم نمودار و مصورسازی (Visualization) عملکرد مدل استفاده خواهد شد.
• شش مورد بعدی، بخش‌های مختلفی از کتابخانه Keras هستند که برای سهولت در کدنویسی هریک به صورت جداگانه به اختصار فراخوانی شده‌اند.

حال تمامی کتابخانه‌های مورد نیاز را فراخوانی کردیم. در اولین قدم کلاس مورد نظر را ایجاد می‌کنیم:

class WORLD:

این کلاس محیطی را شبیه‌سازی خواهد کرد که عامل بتواند دمای یک فضاپیما را تنظیم کنم. دمای این فضاپیما متغیری بین $$-100$$ و $$+100$$ خواهد بود و عامل با تنظیم آن بر روی 0، به بیشترین پاداش ممکن خواهد رسید. عامل نیز در هر «گام» (Step)، 2 عمل برای انجام خواهد داشت:

• کاهش 1 واحدی دما
• افزایش 1 واحدی دما

در ابتدا «متد» (Method) سازنده را ایجاد می‌کنیم. این متد 20 ورودی به شکل زیر خواهد داشت:

    def __init__(self,
                 MinT:typ.Union[int, float]=-100,
                 MaxT:typ.Union[int, float]=+100,
                 nEpisode:int=300,
                 mStep:int=70,
                 qLR:float=9e-1,
                 Gamma:float=9e-1,
                 Epsilon0:float=1,
                 Epsilon1:float=2e-2,
                 nDecayEpisode:int=200,
                 nDense:list[int]=[256, 256],
                 Activation:str='elu',
                 Optimizer:str='Adam',
                 Loss:str='huber',
                 mLR:float=3e-3,
                 nEpoch:int=1,
                 TrainOn:int=16,
                 sBatch:int=32,
                 sMemory:int=1024,
                 Verbose:int=0,
                 RandomState:typ.Union[int, None]=None):

این ورودی‌ها به ترتیب موارد زیر را تنظیم می‌کنند:

• MinT: کمترین دمای ممکن که می‌تواند ایجاد شود. این ورودی به صورت پیش‌فرض بر روی $$-100$$ تنظیم شده است.
• MaxT: بیشترین دمای ممکن که می‌تواند ایجاد شود. این ورودی به صورت پیش فرض بر روی $$+100$$ تنظیم شده است.

دو متغیر فوق برای جلوگیری از افزایش یا کاهش بیش از اندازه دما ایجاد شده‌اند. توجه داشته باشید شبکه‌های عصبی مصنوعی اغلب در بازه مشخصی «تعمیم‌پذیری» (Generalizability) خوبی دارند و نمی‌توان بازه‌های بزرگی را به این منظور استفاده کرد. داده‌های استفاده شده برای آموزش مدل همواره باید توزیع مناسبی در کل بازه ورودی داشته باشند.

سایر ورودی‌ها به ترتیب در زیر آورده شده‌اند.

• nEpisode: تعداد اپیزود‌های آموزش مدل را نشان می‌دهد. مقدار پیشفرض این ورودی بر روی 300 تنظیم می‌شود. تعیین دقیق این اعداد ممکن نیست و اغلب به صورت حدودی و با سعی و خطا است.
• mStep: بیشترین تعداد ممکن گام برای عامل را نشان می‌دهد. با توجه به اینکه بهترین دمای ممکن برابر با 0 است و بیشترین فاصله از این نقطه از این نقطه برابر با 100 است، عامل می‌تواند در 100 گام خود را به این نقطه برساند. بنابراین 70 گام به عنوان پیشفرض می‌تواند مناسب باشد.
• qLR: این ورودی نرخ یادگیری برای Q را نشان می‌دهد. مقدار پیشفرض آن برابر با 0.9 تنظیم شده است، درحالیکه برای Q-Learning از مقدار 0.1 استفاده کردیم.
• Gamma: این ورودی نرخ تخفیف را نشان می‌دهد.
• Epsilon0: مقدار اولیه اپسیلون است که باید بیشتر از 0.9 باشد. به صورت پیشفرض مقدار آن برابر با 1 در نظر گرفته شده است.
• Epsilon1: مقدار نهایی اپسیلون است که باید کمتر از 0.1 باشد. به صورت پیشفرض مقدار آن برابر با 0.02 در نظر گرفته شده است. با توجه به اینکه قصد داریم در فاز دوم، مقدار اپسیلون را تا انتها ثابت نگه داریم، بهتر است Epsilon1 بزرگ‌تر از 0 باشد.
• nDecayEpisode: این ورودی، تعداد اپیزودهای فاز اول را نشان می‌دهد. در طول این تعداد اپیزود اول، مقدار اپسیلون مرتباً کاهش خواهد یافت تا به مقدار نهایی برسد. در ادامه اپیزودها، مقدار اپسیلون ثابت خواهد ماند. مقدار این متغیر همواره باید کمتر از nEpisode باشد. این مقدار به صورت پیش‌فرض برابر با 200 تنظیم شده است که ۶۶ درصد کل اپیزودها را شامل می‌شود.
• nDense: این ورودی یک لیست است که مقادیر داخل آن باید اعدادی صحیح باشند. تعداد این اعداد نشان‌دهنده تعداد لایه‌های پنهان شبکه عصبی مورد استفاده است و مقدار آن‌ها نشان‌دهنده تعداد نورون‌های هر لایه است. با آزمون و خطا در مورد این مسئله، مقدار برای این ورودی انتخاب شده است.
• Activation: این ورودی تابع فعال‌سازی (Activation Function) نورون‌های لایه پنهان شبکه را تعیین می‌کند. مقدار آن به صورت پیشفرض ELU (Exponential Linear Unit) تعیین شده است. این تابع در مقایسه با ReLU (Rectified Linear Unit) عملکرد بهتری نشان می‌دهد و به دلیل داشتن گرادیان غیرصفر برای ورودی‌های منفی، آموزش آن‌ها بهتر و سریع‌تر انجام می‌شود. تابع Sigmoid نیز می‌تواند گزینه مناسب دیگری باشد، اما در صورت استفاده از دو لایه پنهان، می‌تواند بر روی سرعت همگرایی مدل اثر منفی بگزارد. در اغلب موارد، تابع ReLU به عنوان تابع فعال‌سازی لایه‌های پنهان استفاده می‌شود.
• Optimizer: این ورودی الگوریتم بهینه‌ساز شبکه عصبی را نشان می‌دهد. برای بهینه‌سازی مدل‌های Tensorflow الگوریتم‌های متفاوتی وجود دارد که SGD (Stochastic Gradient Descent) و Adam دو مورد از پرکاربردترین آن‌ها است. برای این مسئله، الگوریتم Adam به صورت پیشفرض استفاده خواهد شد.
• Loss: این ورودی تابع هزینه (Loss Function) مورد استفاده برای آموزش شبکه عصبی را نشان می‌دهد. در اغلب مسائل رگرسیون از خطای MSE یا Mean Squared Error استفاده می‌شود. برای مسائل رگرسیونی که داده‌های پرت داریم و قصد داریم اثر آن‌ها را کاهش دهیم نیز از MAE یا Mean Absolute Error استفاده می‌کنیم. اما برای Deep Q-Networkها اغلب Huber Loss توصیه می‌شود.
• mLR: این ورودی نرخ یادگیری شبکه عصبی را تعیین می‌کند. در اغلب موارد، نرخ یادگیری 0.001 استفاده می‌شود اما در این مسئله مقدار 0.003 مناسب است.
• nEpoch: این ورودی تعداد مراحل یا Epoch آموزش مدل بر روی هر Batch را نشان می‌دهد. با توجه به اینکه در این مسئله مجموعه داده‌ای وجود ندارد و عامل با برقرار تعامل با محیط، اطلاعاتی جمع‌آوری می‌کند، باید مدل به جای چندین Batch، هر بار روی تنها 1 Batch آموزش ببیند. بنابراین عدد 1 مناسب است.
• TrainOn: این ورودی تعیین می‌کند که بعد از انجام چند گام توسط عامل، مدل بر روی یک Batch آموزش ببیند. مقدار پیشفرض این متغیر 16 است، بنابراین پس از هر 16 گام، مدل یک مرحله بر روی یک Batch آموزش دیده و وزن‌های آن به‌روزرسانی خواهد شد.
• sBatch: این ورودی سایز Batchها را نشان می‌دهد. این مقدار اغلب از توان‌های 2 انتخاب می‌شود. مقادیر 32، 64 و 128 در اغلب موارد نتایج مطلوبی دارند.
• sMemory: این ورودی سایز حافظه مدل را تعیین می‌کند. یکی از راه‌های جلوگیری از مشکل واگرایی مقادیر Q استفاده از حافظه و آموزش مدل بر روی تجارب قدیمی‌تر است. این ورودی تعیین می‌کند که حداکثر چند تجربه گذشته می‌تواند در آموزش مدل استفاده شود. مقدار 1024 می‌تواند داده‌هایی از 12 اپیزود قبل را در خود جای دهد، بنابراین مناسب خواهد بود. برای مسائل پیچیده‌تر، باید مقدار این متغیر حداقل 20 برابر شود.
• Verbose: شبکه‌های عصبی Tensorflow در طول آموزش و پیشبینی پیام‌هایی مبنی بر میزان پیشرفت و نتایج نمایش می‌دهد. به دلیل استفاده زیاد از این توابع، مقدار بسیار زیادی پیام در خروجی نمایش داده می‌شود که مناسب نیست. به همین دلیل ورودی دیگری به نام Verbose برای این توابع وجود دارد که میزان پرحرف بودن آن‌ها را تنظیم می‌کند. برای اضافه کردن امکان تنظیم این موضوع، ورودی Verbose را ایجاد می‌کنیم. مقدار پیش‌فرض این ورودی 0 است که باعث می‌شود هیچ پیامی از سمت این توابع ایجاد نشود.
• RandomState: تعدادی از فرآیند‌های مربوط به Tensorflow و کدی که می‌خواهیم بنویسیم، از اعداد تصادفی استفاده می‌کنند. به همین دلیل ورودی دیگری نیز ایجاد می‌کنیم تا این فرآیند‌ها را در صورت نیاز کنترل کنیم. مقدار این ورودی می‌تواند یک عدد صحیح یا None باشد. در صورتی که مقدار آن None باشد، فرآیندهای تصادفی در هر بار اجرا به شکل متفاوتی رخ می‌دهند و نتایج قابل بازتولید نخواهد (Not Reproducible) بود. در مقابل با تعیین یک عدد صحیح، نتایج یکسانی تولید خواهد شد. توجه داشته باشید که با تغییر این عدد به عددی دیگر، اعداد تصادفی تولید شده متفاوت با حالت قبلی خواهد بود اما همچنان نتایج قابل بازتولید خواهد بود.

به این ترتیب تمامی ورودی‌های متد سازنده بررسی و توضیح داده شد. حال ورودی‌های دریافت شده را در شیء (Object) ذخیره می‌کنیم تا در متدهای بعدی استفاده کنیم:

    def __init__(self,
                 MinT:typ.Union[int, float]=-100,
                 MaxT:typ.Union[int, float]=+100,
                 nEpisode:int=300,
                 mStep:int=70,
                 qLR:float=9e-1,
                 Gamma:float=9e-1,
                 Epsilon0:float=1,
                 Epsilon1:float=2e-2,
                 nDecayEpisode:int=200,
                 nDense:list[int]=[256, 256],
                 Activation:str='elu',
                 Optimizer:str='Adam',
                 Loss:str='huber',
                 mLR:float=3e-3,
                 nEpoch:int=1,
                 TrainOn:int=16,
                 sBatch:int=32,
                 sMemory:int=1024,
                 Verbose:int=0,
                 RandomState:typ.Union[int, None]=None):
        self.MinT = MinT
        self.MaxT = MaxT
        self.nEpisode = nEpisode
        self.mStep = mStep
        self.qLR = qLR
        self.Gamma = Gamma
        self.Epsilon0 = Epsilon0
        self.Epsilon1 = Epsilon1
        self.nDecayEpisode = nDecayEpisode
        self.nDense = nDense
        self.Activation = Activation
        self.Optimizer = Optimizer
        self.Loss = Loss
        self.mLR = mLR
        self.nEpoch = nEpoch
        self.TrainOn = TrainOn
        self.sBatch = sBatch
        self.sMemory = sMemory
        self.Verbose = Verbose
        self.RandomState = RandomState

متد سازنده در انتها دو متد دیگر را نیز فراخوانی می‌کند که اولی Random State را در صورت نیاز تعیین می‌کند و دومی برخی تنظیمات دیگر را:

    def __init__(self,
                 MinT:typ.Union[int, float]=-100,
                 MaxT:typ.Union[int, float]=+100,
                 nEpisode:int=300,
                 mStep:int=70,
                 qLR:float=9e-1,
                 Gamma:float=9e-1,
                 Epsilon0:float=1,
                 Epsilon1:float=2e-2,
                 nDecayEpisode:int=200,
                 nDense:list[int]=[256, 256],
                 Activation:str='elu',
                 Optimizer:str='Adam',
                 Loss:str='huber',
                 mLR:float=3e-3,
                 nEpoch:int=1,
                 TrainOn:int=16,
                 sBatch:int=32,
                 sMemory:int=1024,
                 Verbose:int=0,
                 RandomState:typ.Union[int, None]=None):
        self.MinT = MinT
        self.MaxT = MaxT
        self.nEpisode = nEpisode
        self.mStep = mStep
        self.qLR = qLR
        self.Gamma = Gamma
        self.Epsilon0 = Epsilon0
        self.Epsilon1 = Epsilon1
        self.nDecayEpisode = nDecayEpisode
        self.nDense = nDense
        self.Activation = Activation
        self.Optimizer = Optimizer
        self.Loss = Loss
        self.mLR = mLR
        self.nEpoch = nEpoch
        self.TrainOn = TrainOn
        self.sBatch = sBatch
        self.sMemory = sMemory
        self.Verbose = Verbose
        self.RandomState = RandomState
        self.SetRandomState()
        self.ApplySettings()

برای پیاده‌سازی متد SetRandomState به شکل زیر عمل می‌کنیم:

    def SetRandomState(self):
        if self.RandomState is not None:
            ran.seed(self.RandomState)
            np.random.seed(self.RandomState)
            tf.random.set_seed(self.RandomState)
            os.environ['PYTHONHASHSEED'] = str(self.RandomState)

توجه داشته باشید که تنها در صورتی Random State را تعیین می‌کنیم که مقدار آن None نباشد. نکته مهم دیگری که باید به آن توجه کرد، وجود Random Seed در کتابخانه‌های مختلف است. بنابراین باید همه آن‌ها در صورت نیاز تنظیم شوند. دو ماژول os و random تنها در این بخش از کد استفاده شده‌اند، اما با توجه به اینکه ممکن است بعداً برای پروژه‌های بزرگ‌تر کدهای بیشتری داشته باشیم، بهتر است ابتدای کد Fix شوند.

حال متد ApplySettings را پیاده‌سازی می‌کنیم. در این متد ابتدا Style مربوط به نمودارها را تنظیم می‌کنیم، سپس برخی قراردادهای مربوط به محیط و عامل را اضافه می‌کنیم:

    def ApplySettings(self):
        plt.style.use('ggplot')
        self.Code2Actions = {0: 'Down', 1: 'Up'}
        self.Action2Change = {0: -1, 1: +1}
        self.nAction = len(self.Code2Actions)

حال شماره اپیزود را نیز بر روی $$-1$$ تنظیم می‌کنیم. با توجه به اینکه در ابتدای هر اپیزود، مقدار آن یک واحد افزایش خواهد یافت، اولین مقدار آن برابر با 0 خواهد بود. حال مقادیر اپسیلون را تعیین می‌کنیم. برای فاز 1 از روند کاهش خطی استفاده می‌کنیم و برای فاز 2 مقدار ثابت نهایی را استفاده می‌کنیم:

        nConstantEpisode = self.nEpisode - self.nDecayEpisode
        epsA = np.linspace(start=self.Epsilon0,
                           stop=self.Epsilon1,
                           num=self.nDecayEpisode)
        epsB = self.Epsilon1 * np.ones(nConstantEpisode)
        self.Epsilons = np.hstack((epsA, epsB))

توجه داشته باشید که تابع numpy.ones آرایه‌ای با ابعاد وارد شده ایجاد می‌کند که تمامی درایه‌های آن برابر با 1 است. ضرب کردن یک عدد اعشاری در آن، باعث تغییر تمامی درایه‌ها به آن عدد خواهد شد.

برای دو فاز، مقادیر اپسیلون در آرایه‌های epsA و epsB ذخیره می‌شود. برای جمع کردن آن‌ها پشت سر هم، می‌توانیم از numpt.hstack استفاده کنیم.

همانند کد قبلی دو آرایه نیز برای ذخیره پاداش هر عمل و مجموع پاداش هر اپیزود ایجاد می‌کنیم:

    def ApplySettings(self):
        plt.style.use('ggplot')
        self.Code2Actions = {0: 'Down', 1: 'Up'}
        self.Action2Change = {0: -1, 1: +1}
        self.nAction = len(self.Code2Actions)
        self.Episode = -1
        nConstantEpisode = self.nEpisode - self.nDecayEpisode
        epsA = np.linspace(start=self.Epsilon0,
                           stop=self.Epsilon1,
                           num=self.nDecayEpisode)
        epsB = self.Epsilon1 * np.ones(nConstantEpisode)
        self.Epsilons = np.hstack((epsA, epsB))
        self.ActionLog = np.zeros((self.nEpisode, self.mStep))
        self.EpisodeLog = np.zeros(self.nEpisode)

حال تابع فعال‌سازی مربوط به لایه خروجی را نیز تعیین می‌کنیم. با توجه به اینکه خروجی شبکه پیوسته است، تنها مقدار مناسب برای تابع فعال‌سازی لایه خروجی تابع خطی (Linear) است، به همین دلیل این متغیر در ورودی دریافت نمی‌شود:

    def ApplySettings(self):
        plt.style.use('ggplot')
        self.Code2Actions = {0: 'Down', 1: 'Up'}
        self.Action2Change = {0: -1, 1: +1}
        self.nAction = len(self.Code2Actions)
        self.Episode = -1
        nConstantEpisode = self.nEpisode - self.nDecayEpisode
        epsA = np.linspace(start=self.Epsilon0,
                           stop=self.Epsilon1,
                           num=self.nDecayEpisode)
        epsB = self.Epsilon1 * np.ones(nConstantEpisode)
        self.Epsilons = np.hstack((epsA, epsB))
        self.ActionLog = np.zeros((self.nEpisode, self.mStep))
        self.EpisodeLog = np.zeros(self.nEpisode)
        self.oActivaiton = 'linear'

حال در این بخش قصد داریم روش دیگری نیز به کار گیریم تا مشکل مربوط به واگرایی مقادیر Q را رفع کنیم. در این روش مقادیر هدف شبکه عصبی را بین یک بیشینه و کمینه مقدار محدود می‌کنیم، به این ترتیب، امکان واگرایی مدل نخواهد بود. به این منظور باید کمترین و بیشترین مقدار پاداش را محاسبه کنیم. ابتدا یک آرایه از 201 شرایط در محدوده مشخص شده انتخاب می‌کنیم. سپس مقادیر پاداش را برای هر کدام محاسبه می‌کنیم:

    def ApplySettings(self):
        plt.style.use('ggplot')
        self.Code2Actions = {0: 'Down', 1: 'Up'}
        self.Action2Change = {0: -1, 1: +1}
        self.nAction = len(self.Code2Actions)
        self.Episode = -1
        nConstantEpisode = self.nEpisode - self.nDecayEpisode
        epsA = np.linspace(start=self.Epsilon0,
                           stop=self.Epsilon1,
                           num=self.nDecayEpisode)
        epsB = self.Epsilon1 * np.ones(nConstantEpisode)
        self.Epsilons = np.hstack((epsA, epsB))
        self.ActionLog = np.zeros((self.nEpisode, self.mStep))
        self.EpisodeLog = np.zeros(self.nEpisode)
        self.oActivaiton = 'linear'
        States = np.linspace(start=self.MinT,
                             stop=self.MaxT,
                             num=201)
        Rewards = self.State2Reward(States)

در این بخش از متد State2Reward استفاده شده است که در ادامه به آن خواهیم پرداخت.

حال کمترین و بیشترین مقدار پاداش را محاسبه می‌کنیم:

    def ApplySettings(self):
        plt.style.use('ggplot')
        self.Code2Actions = {0: 'Down', 1: 'Up'}
        self.Action2Change = {0: -1, 1: +1}
        self.nAction = len(self.Code2Actions)
        self.Episode = -1
        nConstantEpisode = self.nEpisode - self.nDecayEpisode
        epsA = np.linspace(start=self.Epsilon0,
                           stop=self.Epsilon1,
                           num=self.nDecayEpisode)
        epsB = self.Epsilon1 * np.ones(nConstantEpisode)
        self.Epsilons = np.hstack((epsA, epsB))
        self.ActionLog = np.zeros((self.nEpisode, self.mStep))
        self.EpisodeLog = np.zeros(self.nEpisode)
        self.oActivaiton = 'linear'
        States = np.linspace(start=self.MinT,
                             stop=self.MaxT,
                             num=201)
        Rewards = self.State2Reward(States)
        self.MinReward = Rewards.min()
        self.MaxReward = Rewards.max()

با توجه به فرمول مربوط به به‌روزرسانی Qها، می‌توان به صورت حدودی، مقادیر زیر را به عنوان بیشینه و کمینه مقدار Q در نظر گرفت:

    def ApplySettings(self):
        plt.style.use('ggplot')
        self.Code2Actions = {0: 'Down', 1: 'Up'}
        self.Action2Change = {0: -1, 1: +1}
        self.nAction = len(self.Code2Actions)
        self.Episode = -1
        nConstantEpisode = self.nEpisode - self.nDecayEpisode
        epsA = np.linspace(start=self.Epsilon0,
                           stop=self.Epsilon1,
                           num=self.nDecayEpisode)
        epsB = self.Epsilon1 * np.ones(nConstantEpisode)
        self.Epsilons = np.hstack((epsA, epsB))
        self.ActionLog = np.zeros((self.nEpisode, self.mStep))
        self.EpisodeLog = np.zeros(self.nEpisode)
        self.oActivaiton = 'linear'
        States = np.linspace(start=self.MinT,
                             stop=self.MaxT,
                             num=201)
        Rewards = self.State2Reward(States)
        self.MinReward = Rewards.min()
        self.MaxReward = Rewards.max()
        self.MinQ = (1 + self.qLR * self.Gamma) * self.MinReward
        self.MaxQ = (1 + self.qLR * self.Gamma) * self.MaxReward

توجه داشته باشید که این روش تخمینی از مقادیر مرزی است و ممکن است برای برخی مسائل مناسب نباشد.

حال یک حافظه و «شمارنده» (Counter) برای عامل ایجاد می‌کنیم:

    def ApplySettings(self):
        plt.style.use('ggplot')
        self.Code2Actions = {0: 'Down', 1: 'Up'}
        self.Action2Change = {0: -1, 1: +1}
        self.nAction = len(self.Code2Actions)
        self.Episode = -1
        nConstantEpisode = self.nEpisode - self.nDecayEpisode
        epsA = np.linspace(start=self.Epsilon0,
                           stop=self.Epsilon1,
                           num=self.nDecayEpisode)
        epsB = self.Epsilon1 * np.ones(nConstantEpisode)
        self.Epsilons = np.hstack((epsA, epsB))
        self.ActionLog = np.zeros((self.nEpisode, self.mStep))
        self.EpisodeLog = np.zeros(self.nEpisode)
        self.oActivaiton = 'linear'
        States = np.linspace(start=self.MinT,
                             stop=self.MaxT,
                             num=201)
        Rewards = self.State2Reward(States)
        self.MinReward = Rewards.min()
        self.MaxReward = Rewards.max()
        self.MinQ = (1 + self.qLR * self.Gamma) * self.MinReward
        self.MaxQ = (1 + self.qLR * self.Gamma) * self.MaxReward
        self.Memory = co.deque(maxlen=self.sMemory)
        self.Counter = 0

توجه داشته باشید که collections.deque می‌تواند یک بیشینه طول نیز داشته باشد. در صورتی که به بیشینه طول رسیده باشد و مقدار جدیدی به آن اضافه (Append) شود، اولین مقدار موجود (عضو شماره 0 یا سمت چپ) حذف خواهد شد. به این ترتیب حافظه عامل از یک مقدار مشخص بزرگ‌تر نخواهد شد و داده‌های بدون کاربرد به مرور زمان جای خود را به داده‌های جدید خواهد داد. وجود حافظه برای جلوگیری از واگرایی مقادیر Q از اهمیت بالایی برخوردار است. متغیر Counter نیز تعداد داده‌های جدید را نشان می‌دهد که پس از آخرین به‌روزرسانی وزن‌ها اضافه شده‌اند.

مقادیر دما یا همان شرایط عددی در بازه $$[-100,+100]$$ است. این مقیاس می‌تواند در آموزش مدل مشکل‌ساز شود. به همین دلیل مقیاس آن را به بازه $$[-1,+1]$$ تغییر می‌دهیم. به این منظور می‌توانیم تبدیل خطی زیر را انجام دهیم:

$$begin{gathered}
x^{prime}=2 timesleft(frac{x-operatorname{Min}}{operatorname{Max}-operatorname{Min}}right)-1=frac{2 times x-2 times operatorname{Min}}{operatorname{Max}-operatorname{Min}}-1=frac{2 times x-operatorname{Min}-operatorname{Max}}{operatorname{Max}-operatorname{Min}} \
=x timesleft(frac{2}{operatorname{Max}-operatorname{Min}}right)+left(frac{operatorname{Min}+operatorname{Max}}{operatorname{Min}-operatorname{Max}}right)
end{gathered}$$

در رابطه فوق، تنها دو عدد ضریب $$x$$ و عدد ثابت مهم است. به همین دلیل این دو عدد را محاسبه و ذخیره می‌کنیم:

    def ApplySettings(self):
        plt.style.use('ggplot')
        self.Code2Actions = {0: 'Down', 1: 'Up'}
        self.Action2Change = {0: -1, 1: +1}
        self.nAction = len(self.Code2Actions)
        self.Episode = -1
        nConstantEpisode = self.nEpisode - self.nDecayEpisode
        epsA = np.linspace(start=self.Epsilon0,
                           stop=self.Epsilon1,
                           num=self.nDecayEpisode)
        epsB = self.Epsilon1 * np.ones(nConstantEpisode)
        self.Epsilons = np.hstack((epsA, epsB))
        self.ActionLog = np.zeros((self.nEpisode, self.mStep))
        self.EpisodeLog = np.zeros(self.nEpisode)
        self.oActivaiton = 'linear'
        States = np.linspace(start=self.MinT,
                             stop=self.MaxT,
                             num=201)
        Rewards = self.State2Reward(States)
        self.MinReward = Rewards.min()
        self.MaxReward = Rewards.max()
        self.MinQ = (1 + self.qLR * self.Gamma) * self.MinReward
        self.MaxQ = (1 + self.qLR * self.Gamma) * self.MaxReward
        self.Memory = co.deque(maxlen=self.sMemory)
        self.Counter = 0
        self.a = 2 / (self.MaxT - self.MinT)
        self.b = (self.MinT + self.MaxT) / (self.MinT - self.MaxT)

به این ترتیب دو ضریب مورد نیاز برای تغییر مقیاس نیز محاسبه می‌شود.

الگوریتم بهینه‌ساز، تابع هزینه و تابع فعال‌ساز هر سه به شکل «رشته» (String) دریافت شده‌اند. باید این موارد را به شکلی که برای Tensorflow قابل استفاده باشد درآوریم. به این منظور خواهیم داشت:

        self.Optimizer = self.Optimizer.upper()
        self.Loss = self.Loss.upper()
        self.Activation = self.Activation.upper()
        if self.Optimizer == 'ADAM':
            self.Optimizer = opt.Adam(learning_rate=self.mLR)
        elif self.Optimizer == 'SGD':
            self.Optimizer = opt.SGD(learning_rate=self.mLR)
        elif self.Optimizer == 'RMSPROP':
            self.Optimizer = opt.RMSprop(learning_rate=self.mLR)
        if self.Loss == 'MSE':
            self.Loss = los.MeanSquaredError()
        elif self.Loss == 'MAE':
            self.Loss = los.MeanAbsoluteError()
        elif self.Loss == 'HUBER':
            self.Loss = los.Huber(delta=1)
        if self.Activation == 'RELU':
            self.Activation = act.relu
        elif self.Activation == 'ELU':
            self.Activation = act.elu
        elif self.Activation == 'TANH':
            self.Activation = act.tanh

توجه داشته باشید که ممکن است هریک از این موارد به شکل سلیقه‌ای با حروف کوچک، بزرگ یا ترکیبی از آن دو باشد. به همین دلیل در ابتدا ‌آن‌ها را با استفاده از متد upper به حروف بزرگ تبدیل می‌کنیم تا مشکلی از این جهت پیش نیاید. به این ترتیب دو متد مورد استفاده در متد سازنده همگی پیاده‌سازی شدند.

تابع پاداش در پیاده سازی Deep Q Learning

متدی به نام State2Reward نیز در حین کدنویسی استفاده شد که تعریف نشده است. در کد مربوط به Q-Learning به دلیل محدود بودن شرایط، پاداش حالات را به صورت قراردادی مقداردهی می‌کردیم و مشکلی از این جهت نبود. اما در این مسئله به دلیل پیوسته بودن شرایط محیط و دید عامل از محیط (Observation)، نمی‌توان چنین عمل کرد و باید از یک تابع استفاده کنیم. به این منظور از تابع زیر استفاده می‌کنیم:

$$F(x) = 1 -0.002 times x^2$$

این تابع درجه دوم بوده و در نقطه $$x = 0$$ به بیشینه مقدار خود می‌رسد. توجه داشته باشید که در مسائل دنیای واقعی، ما از این تابع مطلع نیستیم و به دنبال تخمین آن هستیم.

در انتهای برنامه نموداری برای این تابع نیز رسم خواهد شد که به شکل زیر خواهد بود:

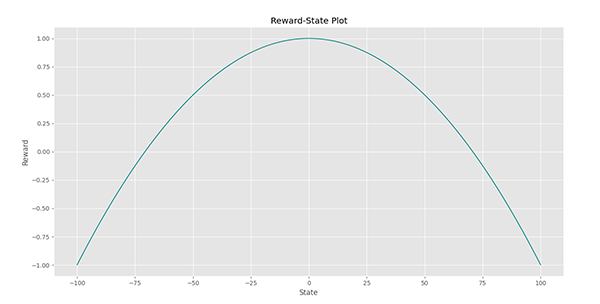
این متد را به شکل زیر تعریف می‌کنیم:

    def State2Reward(self,
                     State:typ.Union[int, float, np.ndarray]) -> typ.Union[float, np.ndarray]:
        Reward = 1 - 0.0002 * State ** 2
        return Reward

توجه داشته باشید که ممکن است این تابع در طول کد به ازای یک State یا چندین State فراخوانی شود. به این دلیل ورودی آن می‌تواند صحیح، غیرصحیح و آرایه باشد. بنابراین باید تمامی این سه حالت در تابع مدنظر گیرد. خوشبختانه به دلیل سازگاری آرایه‌های Numpy با اعمال ریاضی عادی، نیازی به تفکیک ورودی نیست و یک عبارت تمامی حالات را پوشش خواهد داد.

حال می‌توانیم یک متد دیگر رسم کنیم تا نمودار مربوط به State2Reward را در بازه کمترین دما تا بیشترین دما رسم کند:

    def PlotState2Reward(self):
        States = np.linspace(start=self.MinT,
                             stop=self.MaxT,
                             num=201)
        Rewards = self.State2Reward(States)
        plt.plot(States,
                 Rewards,
                 ls='-',
                 lw=1.2,
                 c='teal')
        plt.title('Reward-State Plot')
        plt.xlabel('State')
        plt.ylabel('Reward')
        plt.show()

توجه داشته باشید که در اینجا States یک آرایه است و اگر تابع State2Reward به درست پیاده‌سازی نشده بود، باید یک حلقه ایجاد می‌شد. در سطر داخل بازه معین، 201 نقطه با فاصله یکسان انتخاب می‌شود. در سطر بعدی مقادیر Reward برای هریک محاسبه می‌شود. در نهایت با استفاده از matplotlib.pyplot.plot یک نمودار خطی برای آن رسم می‌شود. نمودار اخیر حاصل این متد است که در انتهای برنامه رسم خواهد شد.

رسم نمودار اپسیلون در پیاده سازی Deep Q Learning

می‌توانیم یک نمودار دیگر نیز برای نمایش مقادیر اپسیلون داشته باشیم. به این منظور متد زیر را پیاده‌سازی می‌کنیم:

    def PlotEpsilons(self):
        T = np.arange(start=1,
                      stop=self.nEpisode + 1,
                      step=1)
        plt.plot(T,
                 self.Epsilons,
                 ls='-',
                 lw=1.2,
                 c='teal')
        plt.title('Epsilon Over Episodes')
        plt.xlabel('Episode')
        plt.ylabel('Epsilon')
        plt.show()

در انتهای کد این متد فراخوانی شده و نمودار زیر را ایجاد خواهد کرد:

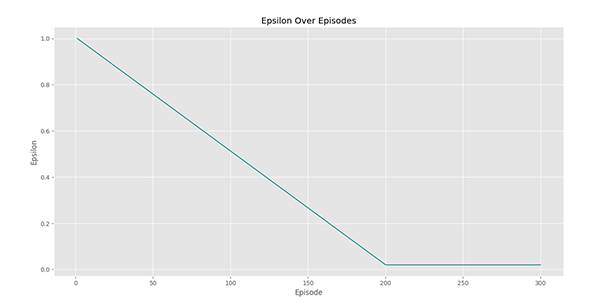
مشاهده می‌کنیم که اپسیلون از Epsilon0 شروع شده و در اپیزود 200 به Epsilon1 می‌رسد. از اپیزود 200 تا 300 نیز مقدار آن ثابت می‌ماند. می‌توان از کاهش نمایی (Exponential Decay) نیز استفاده کرد که اغلب این حالت مورد استفاده قرار می‌گیرد.

در نمودار فوق شاید مقادیر به صورت دقیق قابل تشخیص نباشد. برای رفع این مشکل می‌توان از نمودار «نیمه‌لگاریتمی» (Semi-Logarith) استفاده کرد.

تغییر مقیاس شرایط

حال باید متد دیگری نیز پیاده‌سازی کنیم تا با دریافت State در مقیاس اصلی، آن را به مقیاس $$[-1 , +1]$$ ببرد. به این منظور یک متد ایجاد می‌کنیم و در ورودی شرایط را دریافت می‌کنیم:

    def StateScaler(self,
                    State:typ.Union[int, float, np.ndarray]) -> typ.Union[float, np.ndarray]:

توجه داشته باشید که این متد نیز می‌تواند تنها یک State دریافت کند یا مجموعه‌ای از Stateها را دریافت کند. حال باید State ورودی را در self.a ضرب کرده و با self.b جمع کنیم و مقدار حاصل را در خروجی برگردانیم:

    def StateScaler(self,
                    State:typ.Union[int, float, np.ndarray]) -> typ.Union[float, np.ndarray]:
        ScaledState = self.a * State + self.b
        return ScaledState

به این ترتیب این متد نیز کامل خواهد شد. در مواقعی که بخواهیم خروجی شبکه را دریافت کنیم یا شبکه را بر روی مجموعه داده‌ای آموزش دهیم، باید مقادیر ورودی را با استفاده از این متد Scale کنیم.

ایجاد مدل عمیق

حال می‌توانیم توابع مربوط به مدل عمیق را پیاده‌سازی کنیم. اولین تابع CreateModel خواهد بود که وظیفه آن ایجاد مدل عمیق خواهد بود:

    def CreateModel(self):

با توجه به اینکه قصد داریم یک پرسپترون چندلایه (Multilayer Perceptron یا MLP) ایجاد کنیم، یک مدل Sequential خواهیم داشت. پس یک شی از این کلاس ایجاد می‌کنیم:

    def CreateModel(self):
        self.Model = mod.Sequential()

حال یک لایه ورودی به مدل اضافه می‌کنیم. با توجه به اینکه State تنها شامل یک عدد است، ابعاد ورودی به شکل $$(1 , )$$ خواهد بود:

    def CreateModel(self):
        self.Model = mod.Sequential()
        self.Model.add(lay.InputLayer(input_shape=(1, )))

حال می‌توانیم لایه‌های Dense را به مدل اضافه کنیم. تعداد نورون‌های هر لایه در self.nDense موجود است. بنابراین یک حلقه بر روی این لیست ایجاد می‌کنیم و با استفاده از متد add مربوط به کلاس Sequential، هر لایه را اضافه می‌کنیم:

    def CreateModel(self):
        self.Model = mod.Sequential()
        self.Model.add(lay.InputLayer(input_shape=(1, )))
        for n in self.nDense:
            BI = ini.RandomUniform(minval=-1,
                                   maxval=+1,
                                   seed=self.RandomState)
            self.Model.add(lay.Dense(units=n,
                                     activation=self.Activation,
                                     bias_initializer=BI))

توجه داشته باشید که لایه Dense تنظیمات متعددی دارد که یکی از آن‌ها، bias_initializer است. این ورودی شیوه مقداردهی اولیه (Initialization) بایاس (Bias) را نشان می‌دهد. نورون‌های لایه Dense به صورت پیشفرض بایاس 0 را به عنوان مقدار اولیه به خود می‌گیرند. برای این مسئله می‌توانیم مقادیر اولیه آن‌ها را به صورت یکنواخت در بازه $$[-1 , +1]$$ انتخاب کنیم. توجه داشته باشید که Initializerها نیز یک ورودی seed دارند که این مورد نیز باید با self.RandomState تنظیم شود.

به این ترتیب تا به اینجا لایه ورودی و لایه‌های پنهان اضافه می‌شود. حال باید یک لایه دیگر به عنوان خروجی شبکه ایجاد کنیم و به مدل اضافه کنیم:

    def CreateModel(self):
        self.Model = mod.Sequential()
        self.Model.add(lay.InputLayer(input_shape=(1, )))
        for n in self.nDense:
            BI = ini.RandomUniform(minval=-1,
                                   maxval=+1,
                                   seed=self.RandomState)
            self.Model.add(lay.Dense(units=n,
                                     activation=self.Activation,
                                     bias_initializer=BI))
        BI = ini.RandomUniform(minval=-0.1,
                               maxval=+0.1,
                               seed=self.RandomState)
        self.Model.add(lay.Dense(units=self.nAction,
                                 activation=self.oActivaiton,
                                 bias_initializer=BI))

توجه داشته باشید که تابع فعال‌سازی لایه خروجی متفاوت با لایه‌های پنهان است. از طرفی با توجه به اینکه مقادیر Return در بازه $$[-1 , +1]$$ است، مقادیر بایاس لایه خروجی به احتمال زیاد در بازه‌ای بسیار محدودتر قرار خواهد گرفت، به همین دلیل مقداردهی اولیه آن‌ها بهتر است در بازه‌ای کوچک‌تر و متمرکزتر بر روی میانگین انجام گیرد.

کامپایل کردن مدل

بنابراین با فراخوانی متد قبلی، مدل عمیق ایجاد خواهد شد. مدل‌های Tensorflow علاوه بر ایجاد، نیاز به Compile شدن نیز دارند. به همین دلیل متد دیگری به نام CompileModel ایجاد می‌کنیم:

    def CompileModel(self):
        self.Model.compile(optimizer=self.Optimizer,
                           loss=self.Loss)

در این متد، الگوریتم بهینه‌ساز و تابع هزینه مورد استفاده در آموزش شبکه را تعیین می‌کند.

گزارش ساختار مدل در پیاده سازی Deep Q Learning

حال می‌توانیم متد دیگری ایجاد کنیم تا گزارشی از شبکه را در خروجی چاپ کند:

    def ModelSummary(self):
        self.HL()
        print('Model Summary:')
        self.Model.summary()
        self.HL()

این متد در انتهای کد فراخوانی خواهد شد و نتیجه‌ای به شکل زیر خواهد داشت:

______________________________________________________________________________________________
Model Summary:
Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #
=================================================================
 dense (Dense)               (None, 256)               512

 dense_1 (Dense)             (None, 256)               65792

 dense_2 (Dense)             (None, 2)                 514

=================================================================
Total params: 66,818
Trainable params: 66,818
Non-trainable params: 0
_________________________________________________________________

به این ترتیب می‌توان سایز خروجی لایه‌ها و تعداد پارامترهای آن‌ها را مشاهده کرد. این مدل دارای 66818 پارامتر است.

در متد ModelSummary از متد دیگری به نام HL استفاده شد که وظیفه ایجاد یک خط افقی در خروجی را بر عهده دارد. این متد مشابه کد قبل به شکل زیر تعریف خواهد شد:

    def HL(self, s:str='_', n:int=120):
        print(s * n)

پیش‌بینی با مدل

حال باید متد دیگری نیز پیاده‌سازی کنیم تا با گرفتن یک State یا آرایه‌ای از Stateها، مقادیر آن را نرمال‌سازی (Normalizing) کرده و وارد شبکه کند. در خروجی مقادیر پیشبینی شده برای Q را خواهیم داشت که باید برگردانده شود:

    def PredictQ(self,
                 States:typ.Union[int, float, np.ndarray]) -> np.ndarray:

حال باید مقادیر State را تغییر مقیاس دهیم:

    def PredictQ(self,
                 States:typ.Union[int, float, np.ndarray]) -> np.ndarray:
        ScaledStates = self.StateScaler(States)

با توجه به اینکه در ورودی یک آرایه داشته باشیم یا یک عدد، روش محاسبه مقادیر متفاوت خواهد بود.

بنابراین خواهیم داشت:

    def PredictQ(self,
                 States:typ.Union[int, float, np.ndarray]) -> np.ndarray:
        ScaledStates = self.StateScaler(States)
        if isinstance(States, np.ndarray):
            Q = self.Model.predict(ScaledStates.reshape(-1, 1),
                                   verbose=self.Verbose)
        else:
            Q = self.Model.predict(np.array([[ScaledStates]]),
                                   verbose=self.Verbose)[0]
        return Q

توجه داشته باشید که اگر مقادیر ورودی یک آرایه باشد، در ابعاد $$(n,)$$ خواهد بود بنابراین مقادیر تغییر مقیاس یافته نیز در ابعاد $$(n,)$$ خواهد بود. شبکه عصبی این ورودی‌ها را در ابعاد $$(n,1)$$ قبول می‌کند بنابراین در شرط اول از عبارت reshape(-1, 1) استفاده می‌کنیم.

در شرط دوم مقادیر State و ScaledState تنها یک عدد خواهد بود، بنابراین باید آن را در لیست قرار داده و تبدیل به آرایه کنیم. در این حالت چون تنها یک خروجی داریم، می‌توانیم خروجی برا برای داده اول برگردانیم. عبارتی که در انتهای کد مربوط به else آمده، به همین منظور است.

ذخیره و فراخوانی مدل

آموزش مدل‌های عمیق فرآیندی زمان‌بر است. از طرفی حل مسائل یادگیری تقویتی (Reinforcement Learning) نیز دشواری‌های خود را دارد. بنابراین ذخیره مدل در طول آموزش و فراخوانی مدل‌های آموزش دیده گذشته امری معمول و منطقی است. به همین منظور دو متد دیگر نیز برای ذخیره مدل آموزش دیده (Save) و بارگزاری آن (Load) پیاده‌سازی می‌کنیم:

    def SaveModel(self, Path:str='Model'):
        mod.save_model(self.Model, Path)
        print(col.Fore.MAGENTA + 'Model Saved Successfully.' + col.Fore.RESET)
    def LoadModel(self, Path:str='Model'):
        self.Model = mod.load_model(Path)
        print(col.Fore.MAGENTA + 'Model Loaded Successfully.' + col.Fore.RESET)

به این ترتیب کلاس ایجاد شده، قابلیت استفاده از مدل‌های آموزش دیده قبلی و ذخیره مدل فعلی را نیز خواهد داشت.

ذخیره داده در حافظه

با رخ دادن هر گام در محیط، یک داده جدید ایجاد می‌شود. این داده‌ها باید به ترتیب ایجاد شدن در حافظه عامل ذخیره شوند. به این منظور یک متد ایجاد می‌کنیم که با گرفتن شرایط اولیه، عمل انجام شده، پاداش دریافتی و شرایط نهایی، آن‌ها را به حافظه افزوده و مقدار self.Counter را یک واحد افزایش دهد:

    def Save2Memory(self,
                    State:float,
                    Action:int,
                    Reward:float,
                    State2:float):
        self.Memory.append([State, Action, Reward, State2])
        self.Counter += 1

به این ترتیب مدل دارای حافظه بوده و تعداد داده‌های جدید را به خاطر خواهد سپرد.

آموزش مدل در پیاده سازی Deep Q Learning

پس از ایجاد و کامپایل کردن مدل، می‌توانیم آن را آموزش دهیم. به این منظور نیز یک متد جدید تعریف می‌کنیم.

در این متد فرآیند استفاده از حافظه و معادله Q-Learning استفاده خواهد شد:

    def TrainModel(self):

عامل، به جز 12 اپیزود اول، در سایز اپیزودها، 1024 رکورد (Record) دارد. از بین این 1024 داده، تنها 32 مورد برای آموزش انتخاب خواهد شد. این فرآیند به صورت تصادفی انجام خواهد شد. به این منظور از numpy.random.chice استفاده می‌کنیم:

    def TrainModel(self):
        Selecteds = np.random.choice(len(self.Memory),
                                     size=self.sBatch)

توجه داشته باشید که چون ممکن است طول self.Memory برابر با self.sMemory باشد، باید بیشترین مقدار برابر با طول self.Memory تنظیم شود. در خروجی این کد، 32 داده انتخاب خواهد شد. حال دو آرایه خالی برای ذخیره داده‌ها ایجاد می‌کنیم:

    def TrainModel(self):
        Selecteds = np.random.choice(len(self.Memory),
                                     size=self.sBatch)
        X0 = np.zeros((self.sBatch, 1))
        Y = np.zeros((self.sBatch, self.nAction))

یک حلقه بر روی شماره (Index) داده‌های انتخاب شده ایجاد می‌کنیم:

    def TrainModel(self):
        Selecteds = np.random.choice(len(self.Memory),
                                     size=self.sBatch)
        X0 = np.zeros((self.sBatch, 1))
        Y = np.zeros((self.sBatch, self.nAction))
        for i, j in enumerate(Selecteds):

می‌توان داده مورد نظر را به شکل زیر به 4 متغیر تجزیه کرد:

    def TrainModel(self):
        Selecteds = np.random.choice(len(self.Memory),
                                     size=self.sBatch)
        X0 = np.zeros((self.sBatch, 1))
        Y = np.zeros((self.sBatch, self.nAction))
        for i, j in enumerate(Selecteds):
            State, Action, Reward, State2 = self.Memory[j]

حال مقادیر Q را برای شرایط فعلی و شرایط پس از انجام عمل محاسبه می‌کنیم:

    def TrainModel(self):
        Selecteds = np.random.choice(len(self.Memory),
                                     size=self.sBatch)
        X0 = np.zeros((self.sBatch, 1))
        Y = np.zeros((self.sBatch, self.nAction))
        for i, j in enumerate(Selecteds):
            State, Action, Reward, State2 = self.Memory[j]
            oldOutput1 = self.PredictQ(State)
            oldOutput2 = self.PredictQ(State2)

با توجه به اینکه در شرایط فعلی، تنها یک عمل انتخاب شده و انجام شده است، باید تنها مقدار این خروجی به‌روزرسانی شود:

    def TrainModel(self):
        Selecteds = np.random.choice(len(self.Memory),
                                     size=self.sBatch)
        X0 = np.zeros((self.sBatch, 1))
        Y = np.zeros((self.sBatch, self.nAction))
        for i, j in enumerate(Selecteds):
            State, Action, Reward, State2 = self.Memory[j]
            oldOutput1 = self.PredictQ(State)
            oldOutput2 = self.PredictQ(State2)
            oldQ1 = oldOutput1[Action]

حال می‌توانیم مقدار Temporal Difference را محاسبه کنیم و سپس مقدار جدید Q مورد نظر را محاسبه کنیم:

    def TrainModel(self):
        Selecteds = np.random.choice(len(self.Memory),
                                     size=self.sBatch)
        X0 = np.zeros((self.sBatch, 1))
        Y = np.zeros((self.sBatch, self.nAction))
        for i, j in enumerate(Selecteds):
            State, Action, Reward, State2 = self.Memory[j]
            oldOutput1 = self.PredictQ(State)
            oldOutput2 = self.PredictQ(State2)
            oldQ1 = oldOutput1[Action]
            TD = Reward + self.Gamma * oldOutput2.max() - oldQ1
            newQ1 = oldQ1 + self.qLR * TD

قبل از آموزش مدل بر روی این داده، برای عمل Action در شرایط State، مقدار Q برابر با oldQ1 بود.

حال انتظار داریم که در همان شرایط، برای همان عمل، مقدار Q برابر با newQ1 شود. بنابراین باید Q مربوط به سایر اعمال ثابت بماند. به این منظور یک کپی (Copy) از خروجی قدیمی می‌گیریم و تنها یک مقدار از آن را به‌روزرسانی می‌کنیم:

    def TrainModel(self):
        Selecteds = np.random.choice(len(self.Memory),
                                     size=self.sBatch)
        X0 = np.zeros((self.sBatch, 1))
        Y = np.zeros((self.sBatch, self.nAction))
        for i, j in enumerate(Selecteds):
            State, Action, Reward, State2 = self.Memory[j]
            oldOutput1 = self.PredictQ(State)
            oldOutput2 = self.PredictQ(State2)
            oldQ1 = oldOutput1[Action]
            TD = Reward + self.Gamma * oldOutput2.max() - oldQ1
            newQ1 = oldQ1 + self.qLR * TD
            newOutput1 = oldOutput1.copy()
            newOutput1[Action] = newQ1

به این ترتیب خروجی مد نظر حاصل می‌شود. نکته مهمی که در اینجا وجود دارد، امکان رخ دادن فرآیند خودتنظیمی مثبت و واگرایی مقادیر Q است. برای جلوگیری از این اتفاق، مقادیر این خروجی را بین self.MinQ و self.MaxQ محدود می‌کنیم. به این منظور تابع numpy.clip مناسب است:

    def TrainModel(self):
        Selecteds = np.random.choice(len(self.Memory),
                                     size=self.sBatch)
        X0 = np.zeros((self.sBatch, 1))
        Y = np.zeros((self.sBatch, self.nAction))
        for i, j in enumerate(Selecteds):
            State, Action, Reward, State2 = self.Memory[j]
            oldOutput1 = self.PredictQ(State)
            oldOutput2 = self.PredictQ(State2)
            oldQ1 = oldOutput1[Action]
            TD = Reward + self.Gamma * oldOutput2.max() - oldQ1
            newQ1 = oldQ1 + self.qLR * TD
            newOutput1 = oldOutput1.copy()
            newOutput1[Action] = newQ1
            newOutput1 = np.clip(newOutput1,
                                 a_min=self.MinQ,
                                 a_max=self.MaxQ)

به این ترتیب تا به اینجا دو مکانیسم برای جلوگیری از واگرایی مقادیر Q پیاده‌سازی کردیم. حال داده‌های ایجاد شده را ذخیره می‌کنیم. ورودی شبکه State است و خروجی مورد انتظار newOutput1، بنابراین:

    def TrainModel(self):
        Selecteds = np.random.choice(len(self.Memory),
                                     size=self.sBatch)
        X0 = np.zeros((self.sBatch, 1))
        Y = np.zeros((self.sBatch, self.nAction))
        for i, j in enumerate(Selecteds):
            State, Action, Reward, State2 = self.Memory[j]
            oldOutput1 = self.PredictQ(State)
            oldOutput2 = self.PredictQ(State2)
            oldQ1 = oldOutput1[Action]
            TD = Reward + self.Gamma * oldOutput2.max() - oldQ1
            newQ1 = oldQ1 + self.qLR * TD
            newOutput1 = oldOutput1.copy()
            newOutput1[Action] = newQ1
            newOutput1 = np.clip(newOutput1,
                                 a_min=self.MinQ,
                                 a_max=self.MaxQ)
            X0[i] = State
            Y[i] = newOutput1

پس از اتمام این حلقه، 32 داده خواهیم داشت. تنها موردی که باید انجام شود، تغییر مقیاس X0 است. این تغییر مقیاس را انجام داده و مدل را آموزش می‌دهیم. در نهایت نیز پیامی مبنی بر آموزش مدل نمایش می‌دهیم:

    def TrainModel(self):
        Selecteds = np.random.choice(len(self.Memory),
                                     size=self.sBatch)
        X0 = np.zeros((self.sBatch, 1))
        Y = np.zeros((self.sBatch, self.nAction))
        for i, j in enumerate(Selecteds):
            State, Action, Reward, State2 = self.Memory[j]
            oldOutput1 = self.PredictQ(State)
            oldOutput2 = self.PredictQ(State2)
            oldQ1 = oldOutput1[Action]
            TD = Reward + self.Gamma * oldOutput2.max() - oldQ1
            newQ1 = oldQ1 + self.qLR * TD
            newOutput1 = oldOutput1.copy()
            newOutput1[Action] = newQ1
            newOutput1 = np.clip(newOutput1,
                                 a_min=self.MinQ,
                                 a_max=self.MaxQ)
            X0[i] = State
            Y[i] = newOutput1
        X = self.StateScaler(X0)
        self.Model.fit(X,
                       Y,
                       epochs=self.nEpoch,
                       batch_size=self.sBatch,
                       verbose=self.Verbose)
        print(col.Fore.GREEN + 'Model Trained On Batch.' + col.Fore.RESET)

به این ترتیب این متد خواهد توانست تجارب ذخیره شده در حافظه را به صورت تصادفی انتخاب کرده، داده‌ها را از آن استخراج کند و در نهایت مدل را آموزش دهد.

انتخاب عمل

مشابه مطلب قبلی، یک متد نیز برای انتخاب عمل با توجه به سیاست مورد نظر ایجاد می‌کنیم. این متد در ورودی سیاست مورد نظر را دریافت و در خروجی شماره عمل انتخاب شده را برمی‌گرداند:

    def Decide(self, Policy:str) -> int:
        if Policy == 'R':
            return np.random.randint(low=0, high=self.nAction)
        elif Policy == 'G':
            q = self.PredictQ(self.State)
            return np.argmax(q)
        elif Policy == 'EG':
            if np.random.rand() 

به این ترتیب:

• اگر سیاست ورودی R باشد، «سیاست تصادفی» (Random Policy) در پیش گرفته می‌شود.
• اگر سیاست ورودی G باشد، «سیاست حریصانه» (Greedy Policy) در پیش گرفته می‌شود.
• اگر سیاست ورودی EG باشد، سیاست Epsilon-Greedy در پیش گرفته می‌شود.

ریست کردن شرایط

در ابتدای هر اپیزود، شرایط محیط به حالت اولیه برگردانده می‌شود و گام‌های انجام شده پاک می‌شود. برای انجام این عملیات، متدی به شکل زیر تعریف می‌کنیم:

    def ResetState(self):
        self.State = np.random.uniform(low=self.MinT,
                                       high=self.MaxT)
        self.Step = -1

توجه داشته باشید که در این مسئله، برخلاف مسئله Frozen Lake، محل شروع عامل یکسان نیست و هر بار از محل متفاوتی شروع می‌شود. بنابراین self.State برابر با یک عدد تصادفی در بازه مشخص شده برای دما است.

تعداد گام‌های انجام شده نیز برابر با $$-1$$ تنظیم می‌شود. این تابع در ابتدای هر اپیزود فراخوانی خواهد شد، بنابراین در ابتدای اپیزود برابر با $$0$$ خواهد بود که صحیح است.

اپیزود بعدی

در ابتدای هر اپیزود، باید مشخص کنیم که تغییر اپیزود رخ داده و فرآیندهای مرتبط با آن رخ دهد. این فرآیندها شامل موارد زیر است:

• افزایش Episode
• به‌روزرسانی مقدار Epsilon
• ریست (Reset) کردن شرایط

به این ترتیب می‌توان نوشت:

    def NextEpisode(self):
        self.Episode += 1
        self.Epsilon = self.Epsilons[self.Episode]
        self.ResetState()

توجه داشته باشید که چون تابع ResetState می‌تواند به تنهایی نیز مورد استفاده قرار گیرد، نمی‌توان آن را حذف کرده و دستورات را در NextEpisode نوشت.

گام بعدی

مشابه متد NextEpisode، متد دیگری نیز با نام NextStep ایجاد می‌کنیم:

    def NextStep(self):
        self.Step += 1

ممکن است این ایده به وجود بیاید که می‌توانیم متد‌های کوچک را حذف کنیم و کد مربوط به آن‌ها را در متن اصلی برنامه بنویسیم. با توجه به اینکه این پروژه قابلیت گسترش در قالب‌های مختلف را دارد، در این مقاله سعی بر آن بوده که تمامی متدها وجود داشته باشند. با گسترش کدها، اغلب متدهای آورده شده پیچیده‌تر می‌شوند و فرآیندهای بیشتری را رقم می‌زنند.

انجام عمل

حال به متدی نیاز داریم که با دریافت عمل انتخاب شده، آن را انجام دهد، پاداش حاصل را محاسبه کند، شرایط نهایی را محاسبه کند و شرط اتمام مسئله را نیز بررسی نماید. به این منظور یک متد ایجاد می‌کنیم که در ورودی عمل مورد نظر را به شکل یک عدد صحیح دریافت کند:

    def Do(self, Action:int) -> tuple:

با توجه به اینکه 3 مورد در خروجی برگردانده خواهد شد، خروجی این متد یک تاپل (Tuple) خواهد بود.

حال باید تغییرات حاصل از عمل انجام شده را اعمال کنیم:

    def Do(self, Action:int) -> tuple:
        self.State += self.Action2Change[Action]

برای این منظور، دیکشنری Action2Change استفاده می‌شود که تغییرات دما برای هر عمل را نشان می‌دهد.

حال باید بررسی کنیم تا دما از محدوده مورد نظر ما خارج نشود:

    def Do(self, Action:int) -> tuple:
        self.State += self.Action2Change[Action]
        if self.State > self.MaxT:
            self.State = self.MaxT
        elif self.State 

حال می‌توانیم پاداش حاصل را محاسبه کنیم. به این منظور متد State2Reward مناسب خواهد بود:

    def Do(self, Action:int) -> tuple:
        self.State += self.Action2Change[Action]
        if self.State > self.MaxT:
            self.State = self.MaxT
        elif self.State 

حال شرط اتمام اپیزود را بررسی می‌کنیم و در نهایت خروجی‌های متد را برمی‌گردانیم:

    def Do(self, Action:int) -> tuple:
        self.State += self.Action2Change[Action]
        if self.State > self.MaxT:
            self.State = self.MaxT
        elif self.State 

به این ترتیب متد مربوط به شبیه‌سازی تغییرات حاصل از عامل نیز پیاده‌سازی می‌شود.

رسم خروجی مدل در پیاده سازی Deep Q Learning

برای بررسی شیوه عملکرد مدل و مقادیر خروجی آن، می‌توانیم یک متد دیگر ایجاد کنیم که نمودار متد State2Reward را در کنار خروجی‌های مدل رسم کند:

    def PlotModelPrediction(self, Title:str):

در ابتدا، Stateهایی در بازه مشخص شده ایجاد می‌کنیم:

    def PlotModelPrediction(self, Title:str):
        States = np.linspace(start=self.MinT,
                             stop=self.MaxT,
                             num=201)

حال خروجی متد State2Reward و شبکه عصبی را دریافت می‌کنیم:

    def PlotModelPrediction(self, Title:str):
        States = np.linspace(start=self.MinT,
                             stop=self.MaxT,
                             num=201)
        Rewards = self.State2Reward(States)
        Predictions = self.PredictQ(States)

حال می‌توانیم یک نمودار برای تابع اصلی و دو نمودار برای خروجی شبکه رسم کنیم:

    def PlotModelPrediction(self, Title:str):
        States = np.linspace(start=self.MinT,
                             stop=self.MaxT,
                             num=201)
        Rewards = self.State2Reward(States)
        Predictions = self.PredictQ(States)
        plt.plot(States,
                 Rewards,
                 ls='-',
                 lw=1.4,
                 c='k',
                 label='Reward(State)')
        plt.plot(States,
                 Predictions[:, 0],
                 ls='-',
                 lw=1.2,
                 c='r',
                 label='Q(State, Down)')
        plt.plot(States,
                 Predictions[:, 1],
                 ls='-',
                 lw=1.2,
                 c='b',
                 label='Q(State, Up)')
        plt.title(Title)
        plt.xlabel('State')
        plt.ylabel('Reward / Q')
        plt.legend()
        plt.show()

به این ترتیب این متد قادر خواهد بود به صورت بصری روش تصمیم‌گیری عامل و میزان آموزش مدل را نشان دهد.

آموزش عامل

حال می‌توانیم مهم‌ترین متد یعنی متد Train را پیاده‌سازی کنیم. این متد با استفاده از متدهای پیاده‌سازی شده، مدل عمیق را آموزش خواهد داد و تاریخچه عملکرد عامل نیز ذخیره خواهد شد. این متد تنها سیاست مورد نظر را در ورودی دریافت می‌کند:

    def Train(self, Policy:str='EG'):

حال یک حلقه به ازای تمامی اپیزودها ایجاد می‌کنیم و در ابتدا متد NextEpisode را فراخوانی می‌کنیم:

    def Train(self, Policy:str='EG'):
        for _ in range(self.nEpisode):
            self.NextEpisode()

می‌توان در طول آموزش مدل، نمودارهایی از نتایج آن نمایش داد و آخرین مدل را ذخیره کرد. اما به دلیل زیاد بودن اپیزودها، می‌توانیم از هر 20 اپیزود این فرآیند را تکرار کنیم:

    def Train(self, Policy:str='EG'):
        for _ in range(self.nEpisode):
            self.NextEpisode()
            if self.Episode % 20 == 0:
                self.SaveModel()
                self.PlotModelPrediction(f'Model Prediction For Q Against Real Values (Episode {self.Episode + 1})')

به این ترتیب از هر 20 اپیزود، مدل ذخیره شده و یک نمودار از عملکرد آن نمایش داده می‌شود.

سپس می‌توانیم یک متن نیز از آخرین اپیزود نشان دهیم تا میزان پیشرفت مدل نیز نشان داده شود:

    def Train(self, Policy:str='EG'):
        for _ in range(self.nEpisode):
            self.NextEpisode()
            if self.Episode % 20 == 0:
                self.SaveModel()
                self.PlotModelPrediction(f'Model Prediction For Q Against Real Values (Episode {self.Episode + 1})')
            print(col.Fore.CYAN + f'Episode: {self.Episode + 1} / {self.nEpisode}' + col.Fore.RESET)

حال می‌توانیم حلقه مربوط به گام‌ها را ایجاد کنیم. ابتدا شرایط را دریافت می‌کنیم و سپس یک حلقه While ایجاد می‌کنیم:

    def Train(self, Policy:str='EG'):
        for _ in range(self.nEpisode):
            self.NextEpisode()
            if self.Episode % 20 == 0:
                self.SaveModel()
                self.PlotModelPrediction(f'Model Prediction For Q Against Real Values (Episode {self.Episode + 1})')
            print(col.Fore.CYAN + f'Episode: {self.Episode + 1} / {self.nEpisode}' + col.Fore.RESET)
            State = self.State
            while True:

در ابتدای حلقه، متد NextStep را فراخوانی می‌کنیم. سپس می‌توانیم براساس سیاست وارد شده یک عمل را انتخاب کنیم:

    def Train(self, Policy:str='EG'):
        for _ in range(self.nEpisode):
            self.NextEpisode()
            if self.Episode % 20 == 0:
                self.SaveModel()
                self.PlotModelPrediction(f'Model Prediction For Q Against Real Values (Episode {self.Episode + 1})')
            print(col.Fore.CYAN + f'Episode: {self.Episode + 1} / {self.nEpisode}' + col.Fore.RESET)
            State = self.State
            while True:
                self.NextStep()
                Action = self.Decide(Policy=Policy)

حال عمل انتخاب شده را انجام می‌دهیم و در خروجی، پاداش حاصل، شرایط جدید و متغیر Done را دریافت می‌کنیم:

    def Train(self, Policy:str='EG'):
        for _ in range(self.nEpisode):
            self.NextEpisode()
            if self.Episode % 20 == 0:
                self.SaveModel()
                self.PlotModelPrediction(f'Model Prediction For Q Against Real Values (Episode {self.Episode + 1})')
            print(col.Fore.CYAN + f'Episode: {self.Episode + 1} / {self.nEpisode}' + col.Fore.RESET)
            State = self.State
            while True:
                self.NextStep()
                Action = self.Decide(Policy=Policy)
                Reward, State2, Done = self.Do(Action)

ابتدا تجربه حاصل را در حافظه ذخیره می‌کنیم:

    def Train(self, Policy:str='EG'):
        for _ in range(self.nEpisode):
            self.NextEpisode()
            if self.Episode % 20 == 0:
                self.SaveModel()
                self.PlotModelPrediction(f'Model Prediction For Q Against Real Values (Episode {self.Episode + 1})')
            print(col.Fore.CYAN + f'Episode: {self.Episode + 1} / {self.nEpisode}' + col.Fore.RESET)
            State = self.State
            while True:
                self.NextStep()
                Action = self.Decide(Policy=Policy)
                Reward, State2, Done = self.Do(Action)
                self.Save2Memory(State, Action, Reward, State2)

توجه داشته باشید که در اینجا هر تجربه به شکل زیر است:

$$(s,a,r,s^prime)$$

اما در مسائلی که اتمام اپیزود در شرایط خاصی پس از رسیدن به موقعیت خاص رخ می‌دهد، باید متغیر Done نیز ذخیره شود:

$$(s,a,r,s^prime, done)$$

در این گونه مسائل، به‌روزرسانی مقدار Q به شکل زیر انجام می‌شود:

$$Q(s, a)^{n e w} leftarrowleft{begin{array}{c}
Q(s, a)^{o l d}+alphaleft[r+gamma max _{a^{prime}} Qleft(s^{prime}, a^{prime}right)^{o l d}-Q(s, a)^{o l d}right] text { if not done } \
Q(s, a)^{o l d}+alphaleft[r-Q(s, a)^{o l d}right] text { otherwise }
end{array}right.$$

بنابراین در اینگونه مسائل باید این استثنا در نظر گرفته شود.

حال بررسی می‌کنیم، اگر مقدار self.Counter به self.TrainOn رسیده باشد، مدل را آموزش می‌دهیم و مقدار self.Counter را به 0 برمی‌گردانیم:

    def Train(self, Policy:str='EG'):
        for _ in range(self.nEpisode):
            self.NextEpisode()
            if self.Episode % 20 == 0:
                self.SaveModel()
                self.PlotModelPrediction(f'Model Prediction For Q Against Real Values (Episode {self.Episode + 1})')
            print(col.Fore.CYAN + f'Episode: {self.Episode + 1} / {self.nEpisode}' + col.Fore.RESET)
            State = self.State
            while True:
                self.NextStep()
                Action = self.Decide(Policy=Policy)
                Reward, State2, Done = self.Do(Action)
                self.Save2Memory(State, Action, Reward, State2)
                if self.Counter == self.TrainOn:
                    self.TrainModel()
                    self.Counter = 0

به این ترتیب پس از ذخیره هر 16 تجربه، مدل یک مرحله بر روی 32 تجربه تصادفی موجود در حافظه آموزش می‌بیند.

سپس می‌توانیم پاداش‌های حاصل را نیز ذخیره کنیم:

    def Train(self, Policy:str='EG'):
        for _ in range(self.nEpisode):
            self.NextEpisode()
            if self.Episode % 20 == 0:
                self.SaveModel()
                self.PlotModelPrediction(f'Model Prediction For Q Against Real Values (Episode {self.Episode + 1})')
            print(col.Fore.CYAN + f'Episode: {self.Episode + 1} / {self.nEpisode}' + col.Fore.RESET)
            State = self.State
            while True:
                self.NextStep()
                Action = self.Decide(Policy=Policy)
                Reward, State2, Done = self.Do(Action)
                self.Save2Memory(State, Action, Reward, State2)
                if self.Counter == self.TrainOn:
                    self.TrainModel()
                    self.Counter = 0
                self.ActionLog[self.Episode, self.Step] = Reward
                self.EpisodeLog[self.Episode] += Reward

توجه داشته باشید که می‌توان آرایه self.EposideLog را حذف کرد و در انتها با اعمال متد sum بر روی آرایه self.ActionLog آن را محاسبه کرد.

حال شرایط جدید را جایگزین شرایط قبلی می‌کنیم و در صورت اتمام اپیزود، از حلقه خارج می‌شویم.

    def Train(self, Policy:str='EG'):
        for _ in range(self.nEpisode):
            self.NextEpisode()
            if self.Episode % 20 == 0:
                self.SaveModel()
                self.PlotModelPrediction(f'Model Prediction For Q Against Real Values (Episode {self.Episode + 1})')
            print(col.Fore.CYAN + f'Episode: {self.Episode + 1} / {self.nEpisode}' + col.Fore.RESET)
            State = self.State
            while True:
                self.NextStep()
                Action = self.Decide(Policy=Policy)
                Reward, State2, Done = self.Do(Action)
                self.Save2Memory(State, Action, Reward, State2)
                if self.Counter == self.TrainOn:
                    self.TrainModel()
                    self.Counter = 0
                self.ActionLog[self.Episode, self.Step] = Reward
                self.EpisodeLog[self.Episode] += Reward
                State = State2
                if Done:
                    break

در انتهای اپیزود نیز مجموع پاداش حاصل را نمایش می‌دهیم و یک خط افقی رسم می‌کنیم تا نتایج هر اپیزود از سایرین جدا شود:

    def Train(self, Policy:str='EG'):
        for _ in range(self.nEpisode):
            self.NextEpisode()
            if self.Episode % 20 == 0:
                self.SaveModel()
                self.PlotModelPrediction(f'Model Prediction For Q Against Real Values (Episode {self.Episode + 1})')
            print(col.Fore.CYAN + f'Episode: {self.Episode + 1} / {self.nEpisode}' + col.Fore.RESET)
            State = self.State
            while True:
                self.NextStep()
                Action = self.Decide(Policy=Policy)
                Reward, State2, Done = self.Do(Action)
                self.Save2Memory(State, Action, Reward, State2)
                if self.Counter == self.TrainOn:
                    self.TrainModel()
                    self.Counter = 0
                self.ActionLog[self.Episode, self.Step] = Reward
                self.EpisodeLog[self.Episode] += Reward
                State = State2
                if Done:
                    break
            print(col.Fore.YELLOW + f'Reward: {self.EpisodeLog[self.Episode]:.4f}' + col.Fore.RESET)
            self.HL()

به این ترتیب تا به اینجا می‌توانیم مدل مورد نیازمان را آموزش دهیم.

میانگین متحرک در پیاده سازی Deep Q Learning

حال برای رسم نمودارها، نیاز به متد SMA نیز داریم که در کد قبلی آن را به شکل زیر پیاده‌سازی کردیم:

    def SMA(self, S:np.ndarray, L:int):
        M = np.convolve(S, np.ones(L) / L, mode='valid')
        return M

رسم پاداش اعمال

مشابه کد قبلی، یک متد PlotActionLog ایجاد می‌کنیم و به شکل زیر تعریف می‌کنیم:

    def PlotActionLog(self, L:int=300):
        S = self.ActionLog.reshape(-1)
        M = self.SMA(S, L)
        T = np.arange(start=1,
                      stop=S.size + 1,
                      step=1)
        plt.plot(T,
                 S,
                 ls='-',
                 lw=1.2,
                 c='teal',
                 label='Reward')
        plt.plot(T[-M.size:],
                 M,
                 ls='-',
                 lw=1.4,
                 c='crimson',
                 label=f'SMA({L})') 
        plt.axhline(y=self.MinReward,
                    ls='-',
                    lw=1.2,
                    c='k',
                    label='Min Reward')
        plt.axhline(y=self.MaxReward,
                    ls='-',
                    lw=1.2,
                    c='k',
                    label='Max Reward')
        plt.title('Agent Reward On Each Action')
        plt.xlabel('Action')
        plt.ylabel('Reward')
        plt.legend()
        plt.show()

توجه داشته باشید که دو خط افقی نیز برای نشان دادن کمترین و بیشترین پاداش ممکن برای هر عمل رسم می‌شود تا روند به خوبی نمایش داده شود.

رسم پاداش اپیزودها

برای این متد نیز به شکل مشابه داریم:

    def PlotEpisodeLog(self, L:int=30):
        M = self.SMA(self.EpisodeLog, L)
        T = np.arange(start=1,
                      stop=self.EpisodeLog.size + 1,
                      step=1)
        plt.plot(T,
                 self.EpisodeLog,
                 ls='-',
                 lw=1.2,
                 c='teal',
                 label='Reward')
        plt.plot(T[-M.size:],
                 M,
                 ls='-',
                 lw=1.4,
                 c='crimson',
                 label=f'SMA({L})')
        plt.axhline(y=self.mStep * self.MinReward,
                    ls='-',
                    lw=1.2,
                    c='k',
                    label='Min Reward')
        plt.axhline(y=self.mStep * self.MaxReward,
                    ls='-',
                    lw=1.2, 
                    c='k',
                    label='Max Reward')
        plt.title('Agent Reward On Each Episode')
        plt.xlabel('Episode')
        plt.ylabel('Reward')
        plt.legend()
        plt.show()

توجه داشته باشید که دو خط افقی نیز برای نشان دادن کمترین و بیشترین پاداش ممکن در هر اپیزود رسم می‌شود تا روند به خوبی نمایش داده شود.

آزمایش کردن عامل

حال باید یک متد نیز برای Test کردن عامل ایجاد کنیم. این متد نیز در ورودی سیاست مورد استفاده و رسم یا عدم رسم نمودارها را دریافت می‌کند:

    def Test(self, Policy:str='G', Plot:bool=True):
        self.ResetState()
        print(col.Fore.CYAN + f'Testing Agent:' + col.Fore.RESET)
        States = []
        Rewards = []
        State = self.State
        States.append(State)
        while True:
            self.NextStep()
            Action = self.Decide(Policy=Policy)
            Reward, State2, Done = self.Do(Action)
            States.append(State2)
            Rewards.append(Reward)
            if Done:
                break
        print(col.Fore.YELLOW + f'Reward: {sum(Rewards):.4f}' + col.Fore.RESET)
        self.HL()
        if Plot:
            plt.plot(States,
                     ls='-',
                     lw=1.2,
                     c='teal',
                     label='Temperature')
            plt.axhline(y=self.MinT,
                        ls='-',
                        lw=1.2,
                        c='k',
                        label='Min Temperature')
            plt.axhline(y=self.MaxT,
                        ls='-',
                        lw=1.2,
                        c='k',
                        label='Max Temperature')
            plt.title('Agent State Over Test Episode')
            plt.xlabel('Step')
            plt.ylabel('State')
            plt.legend()
            plt.show()
            T = np.arange(start=1,
                          stop=len(Rewards) + 1,
                          step=1)
            plt.plot(T,
                     Rewards,
                     ls='-',
                     lw=1.2,
                     c='teal',
                     label='Reward')
            plt.axhline(y=self.MinReward,
                        ls='-',
                        lw=1.2,
                        c='k',
                        label='Min Reward')
            plt.axhline(y=self.MaxReward,
                        ls='-',
                        lw=1.2,
                        c='k',
                        label='Max Reward')
            plt.title('Agent Reward Over Test Episode')
            plt.xlabel('Action')
            plt.ylabel('Reward')
            plt.legend()
            plt.show()

این متد علاوه بر نمایش مجموع پاداش حاصل، شرایط محیط را در طول آزمایش نیز ذخیره می‌کند. با رسم نمودار شرایط در طول زمان، می‌توانیم تصمیم عامل در طول اپیزود آزمایش را مشاهده کنیم. نمودار پاداش در طول اپیزود آزمایش نیز رسم می‌شود که مشابه خروجی متد PlotActionLog است.

استفاده از کلاس

حال می‌توانیم از کلاس ایجاد شده، یک شیء بسازیم:

World = WORLD()

می‌توان در صورت نیاز تنظیماتی متفاوت با پیشفرض‌ها اضافه کرد.

حال در اولین قدم می‌توانیم مدل را ایجاد و کامپایل کنیم، سپس گزارش آن را نمایش دهیم:

World = WORLD()

World.CreateModel()
World.CompileModel()
World.ModelSummary()

خروجی متد اخیر در حین کدنویسی به عنوان نمونه نتیجه آورده شده است.

حال می‌توانیم نمودار مربوط به اپسیلون و متد State2Reward را نیز رسم کنیم:

World.PlotEpsilons()
World.PlotState2Reward()

این دو نمودار نیز در طول کدنویسی آورده شده‌اند.

حال می‌توانیم مدل را آموزش دهیم:

World.Train()

اتمام کار این متد زمان‌بر است. برای دو اپیزود اول، نتایج به شکل زیر خواهد بود:

Model Saved Successfully.
Episode: 1 / 300
Model Trained On Batch.
Model Trained On Batch.
Model Trained On Batch.
Model Trained On Batch.
Reward: 63.4474
______________________________________________________________________________________________
Episode: 2 / 300
Model Trained On Batch.
Model Trained On Batch.
Model Trained On Batch.
Model Trained On Batch.
Reward: 9.2524

به این ترتیب مشاهده می‌کنیم که مدل مطابق آنچه کدنویسی شده است، درحال آموزش است. در حین اجرای این متد، پس از هر 20 اپیزود، مدل نهایی ذخیره شده و نمودار PlotModelPrediction رسم می‌شود.

اولین نمودار PlotModelPrediction به شکل زیر است:

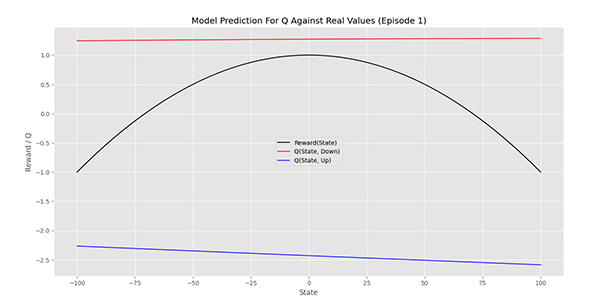
به این ترتیب مشاده می‌کنیم که برای تمامی شرایط، عمل 0 که مربوط به کاهش دما است، دارای Q بالاتری است (این مدل هیچگونه آموزشی ندیده است).

در ابتدای اپیزود 21 به نتیجه زیر می‌رسیم:

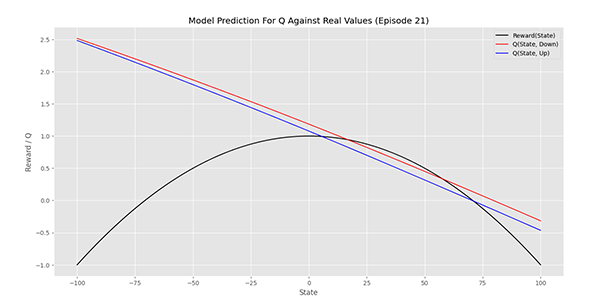
مشاهده می‌کنیم که هر دو نمودار به همدیگر نزدیکه شده‌اند و در بازه 10 تا 60 نیز همپوشانی خوبی با تابع هدف دارند.

در ابتدای اپیزود 221 نمودار به شکل زیر درمی‌آید:

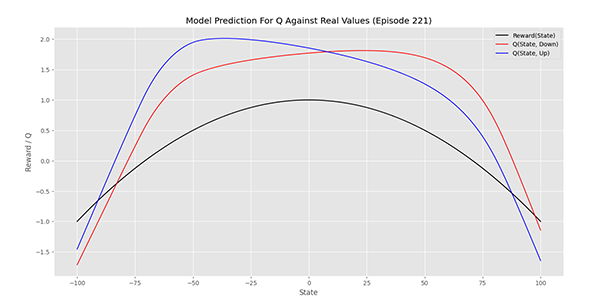
مشاهده می‌کنیم که در بازه $$-100$$ تا $$+10$$ افزایش دما دارای Q بیشتری است درحالیکه از $$+10$$ تا $$+100$$ کاهش دما دارای Q بیشتری است. بنابراین این شبکه می‌تواند بسیار مناسب باشد. اما این نمودار همپوشانی خوبی با نمودار اصلی ندارد، بنابراین ادامه آموزش می‌تواند مدل‌های بهتری ایجاد کند.

در انتهای آموزش کد زیر را اجرا می‌کنیم:

World.PlotModelPrediction('Model Prediction For Q Against Real Values (Final)')

که نمودار زیر حاصل می‌شود:

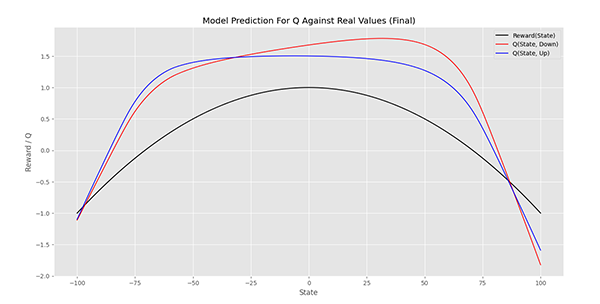
مشاهده می‌کنیم که نمودار به هم خورده است و تصمیم‌گیری‌های اشتباهی رخ می‌دهد. اما این نمودار همپوشانی بهتری با نمودار هدف دارد. بنابراین باید مدل بیشتر از 300 اپیزود آموزش ببیند. به این منظور می‌توان از مدل ذخیره شده استفاده کرد.

حال مدل نهایی را ذخیره می‌کنیم:

World.SaveModel()

در نتیجه خواهیم داشت:‌

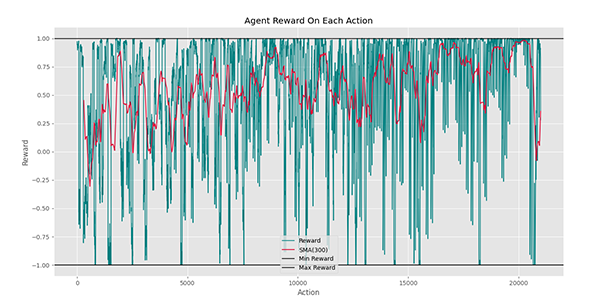
مشاهده می‌کنیم که به طور کلی، روند عامل رو به بهبود بوده است. پرش‌های رخ داده در نمودار، به دلیل شروع هر اپیزود از یک دمای تصادفی است. توجه داشته باشید که ممکن است کم بودن پاداش در برخی حالات، به دلیل دور بودن عامل از ­نقطه 0 باشد.

می‌توانیم به شکل مشابه مجموع پاداش هر اپیزود را نیز رسم کنیم:

World.PlotEpisodeLog()

که خواهیم داشت:‌

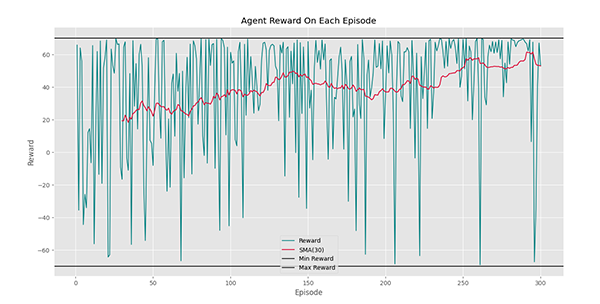
به این ترتیب در این نمودار روند افزایش به خوبی مشهود است.

توجه داشته باشید که نتایج آورده شده تا به این نقطه مطلب با تنظیمات TrainOn=32 حاصل شده‌اند. بنابراین امکان تفاوت در نتایج وجود خواهد داشت.

حال می‌توانیم در یک کد دیگر، مدل آموزش دیده نهایی را فراخوانی کرده و با تنظیمات زیر به آموزش آن ادامه دهیم:

World = WORLD(nEpisode=140,
              qLR=0.5,
              Epsilon0=0.5,
              Epsilon1=0.01,
              nDecayEpisode=139,
              TrainOn=64,
              sBatch=32)

World.LoadModel()

World.Train()

World.PlotModelPrediction('Model Prediction For Q Against Real Values (Final)')

World.SaveModel(Path='Model1')

World.PlotActionLog()

World.PlotEpisodeLog()

در خروجی کد فوق، نتیجه نهایی به شکل زیر خواهد بود:

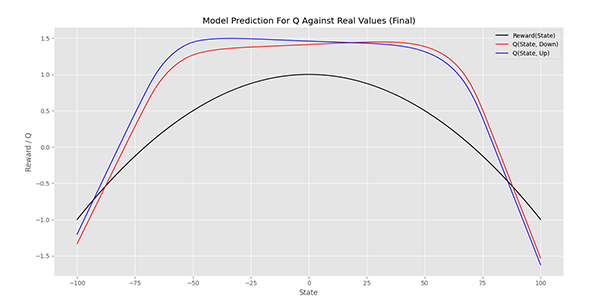
توجه داشته باشید که همچنان مدل می‌تواند بهبود یابد. تغییر تنظیمات مدل، می‌تواند بیشتر از افزایش مراحل آموزش مدل اثربخش باشد.

حال می‌توانیم مدل را آزمایش کنیم. با توجه به اینکه مدل هربار از نقطه متفاوتی شروع به کار می‌کند، می‌توانیم داخل یک حلقه، چندین بار عامل را آزمایش کنیم:

for _ in range(10):
    World.Test()

در این شرایط نمودارها به شکل زیر خواهد بود:

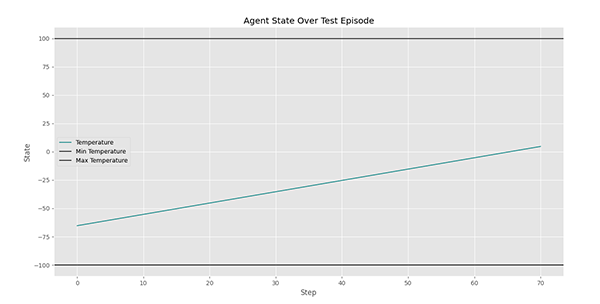
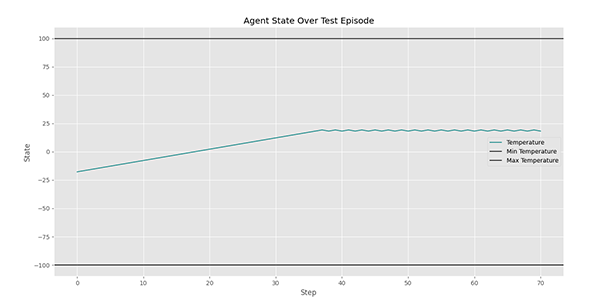
 در نمودار فوق، دمای فضاپیما در طول آزمایش نشان داده می‌شود. مشاهده می‌کنیم که در ابتدا، عامل با دمای نزدیک $$-60$$ شروع به کار کرده و در نهایت توانسته است دما را به حدود $$+10$$ برساند. بنابراین عملکرد مناسب داشته. برای این آزمایش، پاداش هر گام به شکل زیر ظاهر می‌شود.

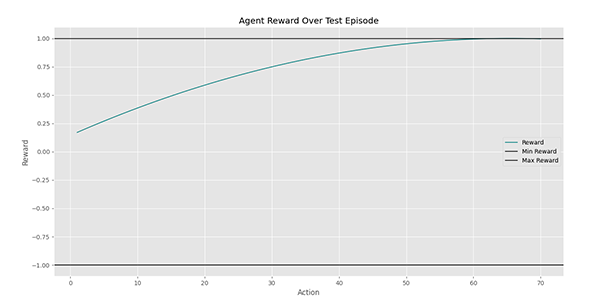
در این نمودار مشاهده می‌کنیم که در ابتدا عامل در شرایطی با ارزش 0٫2 قرار داشته اما در نهایت توانسته خود را به شرایطی با ارزش 1 برساند. بنابراین عامل به هدف خود رسیده است. در یک آزمایش دیگر، نتایج به شکل زیر ظاهر می‌شود:

مشاهده می‌کنیم که عامل با دمای نزدیک به $$-20$$ درجه شروع کرده و پس از رسیدن به دمای $$+20$$، در هر گام عکس عمل گام قبلی را انجام داده تا دما را در حد مطلوب خود نگه دارد. برای این آزمایش، نمودار پاداش هر گام به شکل زیر است:

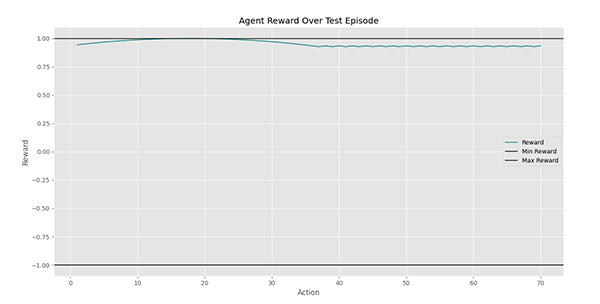
مشاهده می‌کنیم که عامل پاداش خود را در ناحیه بالای $$+0.9$$ حفظ کرده است.

می‌توان با گرفتن اجراهای بیشتر، عملکرد عامل را به خوبی درک کرد.

جمع‌‌بندی پیاده سازی Deep Q Learning در پایتون

به این ترتیب پیاده سازی Deep Q Learning به اتمام می‌رسد. برای مطالعه بیشتر، می‌توان موارد زیر را بررسی کرد:

1. چرا عامل در آخرین نمودار، از نقطه بیشینه گذشته و بر روی خود را تثبیت کرد؟
2. چرا در بازآموزی مدل، نرخ یادگیری Q را کاهش دادیم؟
3. چرا در بازآموزی مدل، مقدار TrainOn و sBatch را دوبرابر کردیم؟
4. اگر در هر بار Reset کردن شرایط محیط، از یک نقطه ثابت شروع می‌کردیم، چه اتفاقی رخ میداد؟ برای انجام این حالت چه کاری باید انجام داد؟
5. با کاهش sMemory به 32، بررسی کنید یادگیری مدل به چه صورت پیش خواهد رفت؟
6. برای ذخیره مدل‌های تنسورفلو، دو فرمت از فایل‌ها وجود دارد. با مراجعه به داکیومنت (Document) این کتابخانه، این دو فرمت را بیابید.
7. به‌جز 3 سیاست پیاده‌سازی شده، سیاست‌های دیگری نیز برای تصمیم‌گیری وجود دارد. یکی از این سیاست‌ها، سیاست بولتزمان (Boltzmann Policy) است. این سیاست را پیاده‌سازی کرده و مدل عمیق را با استفاده از آن آموزش دهید.
8. اگر متد StateScaler را استفاده نکنیم، آموزش مدل به چه شکل خواهد بود؟
9. اگر مقادیر Q را بین MinQ و MaxQ محدود نکنیم، آموزش مدل به چه شکل خواهد بود؟
10. اگر بخواهیم به جای 2 عمل، 3 عمل داشته باشیم و یک حالت مربوط به عدم تغییر باشد، کد باید به چه شکلی نوشته شود؟
11. متد TrainModel را با استفاده از محاسبات برداری Numpy بازنویسی کنید و از حلقه for استفاده نکنید.
12. برخی شروط در رابطه با ورودی‌های متدها داشتیم. برقراری این شروط را بررسی کنید و در صورت نیاز با assert آن‌ها را به عنوان خطا برگردانید.
13. اگر bias_initializer مربوط به لایه‌های Dense را به حالت پیشفرض برگردانیم، آموزش مدل به چه صورت خواهد بود؟
14. در مورد خطای Huber تحقیق کنید.
15. در مورد توابع فعال‌سازی موجود در کتابخانه Tensorflow تحقیق کنید.