تحلیل سرشکن در طراحی الگوریتم — به زبان ساده

«تحلیل سرشکن» یا «آنالیز استهلاکی» (Amortized Analysis) در طراحی الگوریتم، نوعی تحلیل برای یک الگوریتم به حساب می‌آید که بخش دشوارتر همراه با «پیچیدگی زمانی» (Time complexity) بالاتر، اما با اهمیت بیشتری را دربرمی‌گیرد. این تحلیل ممکن است با روش‌های گوناگونی در بسیاری از الگوریتم‌ها و «ساختمان داده‌ها» (Data Structure) نیاز باشد. در این مطلب سعی شده است به طور جامع و همراه با مثال‌های کاربردی به این سوال پاسخ داده شود که تحلیل سرشکن در طراحی الگوریتم چیست.

تحلیل سرشکن در طراحی الگوریتم چیست ؟

تحلیل سرشکن در طراحی الگوریتم، روشی برای تجزیه و تحلیل «هزینه» (Cost) ساختمان داده یا الگوریتمی است که میانگین بدترین هزینه عملیات در طول زمان را نشان می‌دهد. گاهی اوقات الگوریتم یا ساختمان داده‌ای دارای عملیات پرهزینه خاصی است که در بیشتر مواقع انجام نمی‌شوند، اما اغلب یک ساختمان داده تنها دارای یک عملیات پرهزینه است، اما این عملیات در اغلب اوقات اجرا نمی‌شود و به ندرت اتفاق می‌افتد. در این مطلب، تحلیل سرشکن در طراحی الگوریتم به عنوان رویکردی برای تخمین هزینه «زمان اجرا» (Run-Time) روی یک دنباله از عملیات به طور جامع بررسی می‌شود.

بنابراین، تحلیل سرشکن در طراحی الگوریتم برای پیدا کردن میانگین عملیات پرهزینه در بدترین حالت استفاده می‌شود. این بدترین حالت می‌تواند بدترین سناریو برای ساختمان داده، بدترین ترتیب عملیات از نظر ایجاد هزینه بالا و بسیاری موارد دیگر باشد. زمانی که این حالت در عملیات پیدا شد، می‌توان میانگین هزینه عملیات را به دست آورد. سه نوع تحلیل سرشکن در طراحی الگوریتم اصلی وجود دارد که در ادامه فهرست شده‌اند و در بخش‌های بعدی به طور جامع به آن‌ها پرداخته شده است:

• «تحلیل تجمعی» (Aggregate Analysis)
• «روش حسابرسی» (Accounting Method)
• «روش پتانسیل» (Potential Method)

بینش موجود در پشت تحلیل سرشکن در طراحی الگوریتم و دلیل استفاده از آن بسیار مهم است. اگر عملیاتی نسبتاً غیرمعمول وجود داشته باشد، یک عمل بد نباید در روند کل الگوریتم مشکلی به وجود بیاورد. از نظر فنی، هدف این است که درک شود، ساختمان داده‌ و الگوریتم‌ها چگونه عمل می‌کنند و تحلیل سرشکن در طراحی الگوریتم به فرد کمک می‌کند تا این کار را با ارائه یک توصیف دقیق از ساختمان داده در طول زمان اجرا انجام دهد. نگاه کردن به بدترین عملکرد در طول عملیات روش بدبینانه‌ای به حساب می‌آید و تحلیل سرشکن تصویر واضح‌تری از آن‌چه که در حال وقوع است به فرد می‌دهد.

به این نکته نیز درباره تحلیل سرشکن در طراحی الگوریتم باید اشاره کرد که با توجه این‌که این موضوع بخشی از سرفصل‌های درس طراحی الگوریتم به حساب می‌آید، معمولاً به طور مستقیم در کنکور کارشناسی ارشد و دکتری رشته‌های مهندسی کامپیوتر سوالی از آن طرح نمی‌شود، اما ممکن است سوالات بخش‌های دیگر با تحلیل سرشکن در طراحی الگوریتم ارتباط داشته باشند. به همین دلیل یادگیری این مطلب برای دانشجویان مهم است. ادامه این مطلب به مثالی از دنیای واقعی برای درک بهتر تحلیل سرشکن در طراحی الگوریتم اختصاص دارد.

مثالی از دنیای واقعی برای تحلیل سرشکن در طراحی الگوریتم

برای مثال فردی قصد پختن کیک برای فروش دارد. پختن کیک نسبتاً کار پیچیده‌ای به حساب می‌آید، اما دارای دو مرحله اصلی زیر است:

• مخلوط کردن خمیر و مواد اولیه که با سرعت بالا انجام می‌شود.
• پختن کیک داخل فر که با سرعت پایین انجام و همچنین فقط یک کیک در هر لحظه در زمانی مشخص پخته می‌شود.

مخلوط کردن مواد اولیه کیک نسبتاً در مقایسه با پختن آن زمان کمتری می‌برد. پس از آن، فرد در مورد فرایند درست کردن کیک فکر می‌کند. این فرایند تصمیم‌گیری، دارای زمان‌های کُند، متوسط و سریع است. در این حالت فرایند متوسط انتخاب می‌شود؛ زیرا برای رسیدن به دو فرایند سریع و کند می‌توان از میانگین آن‌ها یعنی حالت متوسط استفاده کرد. حال فرض می‌شود که قرار است ۱۰۰ کیک پخته شود، برای این کار دو روش وجود دارد، روش اول این است که خمیری برای کیک آمده و سپس پخته شود و روش دوم این است که ابتدا همه خمیرها برای ۱۰۰ کیک آماده‌سازی شوند و سپس فرد همه آن‌ها را یکی پس از دیگری بپزد.

حال باید آهسته، متوسط و سریع بودن این روش‌ها بررسی شوند. تجزیه و تحلیل سرشکن در این مورد هر دو روش را متوسط در نظر می‌گیرد؛ یعنی اگر مواد اولیه هر کدام از ۱۰۰ کیک به صورت جداگانه آماده و پخته شود، باز هم این روش متوسط در نظر گرفته می‌شود. زیرا در حالت سریع‌تر بعد از انجام ۱۰۰ عملیات با یکدیگر، دوباره نیاز است که ۱۰۰ عملیات جداگانه متوسط برای پخت انجام شوند و میانگین این کارها، عملیاتی متوسط ایجاد می‌کند. بدترین حالت در این مثال حالتی است که در آن نمی‌توان توالی بدتری از رویداد‌ها را انتخاب کرد و همچنین نمی‌توان از عملیات مخلوط کردن مواد اولیه کیک صرف نظر کرد و کیک پخت.

همچنین، فرایند پخت در هر صورت آهسته پیش می‌رود و ارزش تجزیه و تحلیل ندارد. در نهایت می‌توان گفت که فرایند پخت کیک فرایندی متوسط ​​به حساب می‌آید؛ زیرا مخلوط کردن مواد اولیه کیک و پخت آن دارای نظم منطقی است که قابل تغییر نیست. در ادامه این مطلب، پیچیدگی زمانی تحلیل سرشکن در طراحی الگوریتم را یاد می‌گیریم.

زمان سرشکن روشی برای نشان دادن پیچیدگی زمانی است که هر چند وقت یک بار برای الگوریتم در شرایط بد ایجاد می‌شود و این زمان با آن پیچیدگی معمول تفاوت دارد که همیشه برای الگوریتم اتفاق می‌افتاد. مثال خوبی که برای این مفهوم می‌توان بیان کرد، بررسی یک «ArrayList» است که ساختمان داده‌ای حاوی یک «آرایه» (Array) با قابلیت گسترش به حساب می‌آید. تعاریف دیگری نیز برای مفهوم پیچیدگی زمانی تحلیل سرشکن وجود دارند، برای مثال در تعریف وب سایت «Stack Overflow»، پیچیدگی زمانی سرشکن در طراحی الگوریتم را می‌توان میانگین زمان صرف شده برای هر عمل در حالتی در نظر گرفت که عملیات زیادی در آن انجام می‌شود.

زمانی که ساختمان داده ArrayList ظرفیت آرایه خود را به اتمام رساند، یک آرایه جدید با دو برابر اندازه آرایه قدیمی ایجاد و همه موارد موجود در آرایه قدیمی را در آرایه جدید کپی می‌کند. در ArrayList دو پیچیدگی زمانی وجود دارد، یکی از آن‌ها $$O(1)$$ و دیگری $$O(n)$$ است. در این مثال، برای درج موارد در آرایه، فقط نیاز است که هر مورد را پس از مورد قبلی در آرایه قرار داد و تا زمانی که فضا برای درج عنصر وجود داشته باشد، نیازی به ایجاد آرایه جدید نیست.

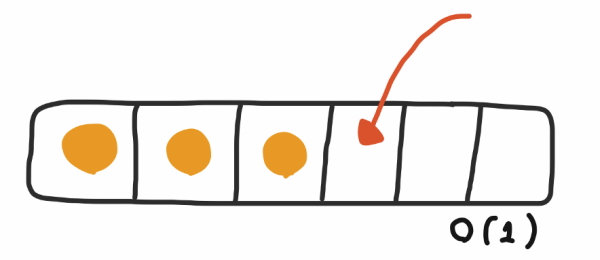
زمانی که ظرفیت آرایه تکمیل می‌شود و دیگر فضایی برای قرار گرفتن موارد جدید در آرایه وجود ندارد، باید یک آرایه جدید با ظرفیت دو برابر قبلی ایجاد شود و سپس موارد موجود در آرایه قبلی را در این آرایه جدید کپی کرد. پیچیدگی زمانی این فرایند برابر با $$O(n)$$ است که در آن n

 ظرفیت آرایه قدیمی در بدترین حالت در نظر گرفته می‌شود.

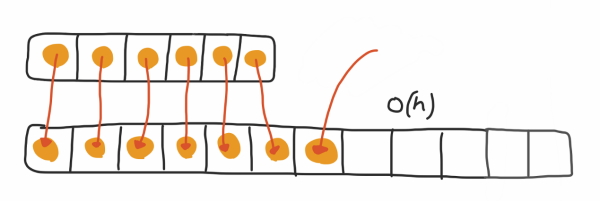
پیچیدگی زمانی سرشکن در طراحی الگوریتم در این مثال تعریف شده و مختص به این بخش از الگوریتم است. این پیچیدگی زمانی امکانی را فراهم می‌کند تا هنگامی که آرایه به حداکثر ظرفیت خود می‌رسد، آن را به عنوان بدترین حالت خود توصیف کند. در ادامه این مطلب، کاربرد تحلیل سرشکن در طراحی الگوریتم بررسی می‌شود.

کاربرد تحلیل سرشکن در طراحی الگوریتم چیست ؟

تحلیل سرشکن در الگوریتم‌هایی مورد استفاده قرار می‌گیرد که در آن‌ها «عملیات مقطعی» (Occasional Operation) بسیار کُند پیش می‌رود. اما بیشتر عملیات دیگر در الگوریتم سریع هستند. در تجزیه و تحلیل سرشکن، دنباله‌ای از عملیات تجزیه و تحلیل می‌شوند و تضمین خواهد شد که ز‌مان میانگین بدترین حالت، کمتر از بدترین حالت یک عمل با ارزش است.

نمونه‌ای از ساختمان داده‌هایی که تحلیل سرشکن در عملیات آن‌ها کاربرد دارد، شامل «جدول درهم‌سازی» (Hash Table)، «مجموعه جدا از هم» (Disjoint Set) و «درخت گسترده» (Splay Tree) می‌شود. در ادامه مثالی از «درج» (Insertion) در جدول درهم‌سازی برای تحلیل سرشکن در طراحی الگوریتم بیشتر توضیح داده شده است.

تحلیل سرشکن در جدول درهم سازی

در این بخش یک جدول درهم‌سازی در نظر گرفته شده است که عملیات درج در آن انجام خواهد شد. مسئله این است که چگونه باید در مورد اندازه جدول تصمیم گرفته شود؟ در این مثال بین زمان و فضا یک رابطه وجود دارد که اگر طبق این رابطه اندازه جدول درهم‌سازی بزرگ شود، زمان جستجو کم می‌شود، اما فضای مورد نیاز زیاد خواهد شد. در ادامه مثال این جدول مشاهده می‌شود:

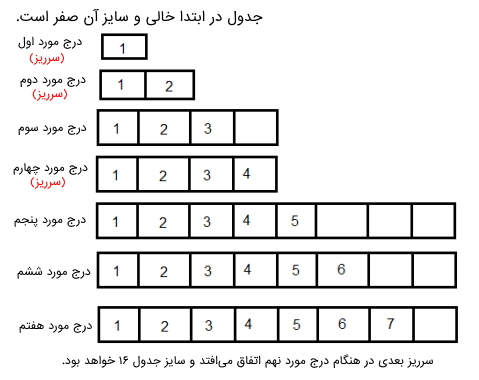
راه حل مقابله با مشکل «سرریز» (Overflow) به وجود آمده، استفاده از «جدول‌های پویا» (Dynamic Table) یا آرایه‌ها است. ایده این راه حل به این صورت است که هر زمان جدول پر شد، اندازه آن را باید افزایش داد. در ادامه مراحلی فهرست شده‌اند که نیاز است هنگام پر شدن جدول دنبال شوند:

1. حافظه به جدولی با اندازه بزرگتر اختصاص داده می‌شود، این اندازه معمولاً دو برابر جدول قبلی است.
2. محتوای جدول قدیمی به جدول جدید کپی می‌شود.
3.  در این مرحله جدول قدیمی رها شده است.

البته اگر جدول فضای قابل استفاده داشته باشد، به سادگی می‌توان موارد جدید را در آن فضای موجود درج کرد. در بخش بعدی از مطلب «تحلیل سرشکن در طراحی الگوریتم» به بررسی پیچیدگی زمانی n

 درج در جدول درهم‌سازی می‌پردازیم.

پیچیدگی زمانی چند درج در جدول درهم سازی چقدر است؟

اگر برای بررسی پیچیدگی زمانی از یک تحلیل ساده استفاده شود، بدترین هزینه یک درج $$O(n)$$ است. بنابراین بدترین هزینه n

 درج برابر با $$n * O(n)$$ و به عبارت دیگر $$O(n^2)$$ در نظر گرفته می‌شود. این تحلیل‌ها «کران بالا» (Upper Bound) را ارائه می‌دهند، اما یک کران بالا اکید را برای n

 درج نشان نمی‌دهند؛ زیرا همه درج‌ها برابر با $$O(n)$$ نیست.

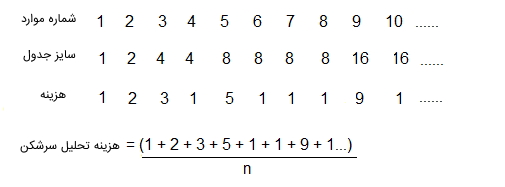
می‌توان سری تصویر بالا را با استفاده از شکستن موارد ۲، ۳، ۵ و ۹ به عبارت‌های (۱+۱)، (۱+۲)، (۱+۴) و (۱+۸) ساده کرد. یعنی رابطه تحلیل سرشکن در طراحی الگوریتم برای این مثال به صورت زیر نوشته شود.

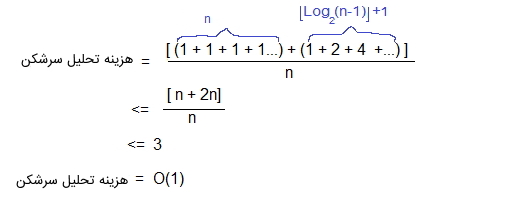
بنابراین، با استفاده از تجزیه و تحلیل سرشکن، می‌توان ثابت کرد که طرح جدول پویا دارای زمان درج $$O(1)$$ است که این زمان نتیجه عالی در استفاده از درهم‌سازی به حساب می‌آید. به طور کلی جدول پویا در بردارهای زبان‌های ++C و «ArrayList» زبان «جاوا» (Java) استفاده می‌شود. در ادامه این مطلب، نکته‌هایی درباره تحلیل سرشکن در طراحی الگوریتم ارائه شده‌اند.

نکته های مهم تحلیل سرشکن در طراحی الگوریتم

در این بخش چند نکته بسیار مهم درباره تحلیل سرشکن در طراحی الگوریتم ارائه شده است. برای مثال، هزینه تحلیل سرشکن یک دنباله از عملیات را می‌توان به عنوان هزینه‌های یک فرد حقوق بگیر در نظر گرفت. میانگین هزینه ماهیانه فرد برابر یا کمتر از حقوق است، اما این فرد می‌تواند در برخی از ماه‌ها با خرید بیشتری مانند خرید ماشین پول بیشتری خرج کند و در ماه‌های دیگر برای ماه‌هایی که خرج بیشتری دارد، پول خود را پس‌انداز کند.

این تجزیه و تحلیل سرشکن در طراحی الگوریتم برای مثال در «آرایه‌های پویا» (Dynamic Array) انجام می‌شود و به آن روش تجمعی می‌گویند. دو روش قوی‌تر دیگر نیز با نام‌های روش حسابرسی و روش پتانسیل وجود دارند که تحلیل سرشکن را انجام می‌دهند. در بخش‌های بعدی این روش‌ها به طور جامع و با مثال شرح داده می‌شوند. به طور کلی تحلیل سرشکن در طراحی الگوریتم شامل احتمال نمی‌شود. همچنین مفهوم متفاوت دیگری از زمان اجرای متوسط وجود دارد که در آن الگوریتم‌ها از «تصادفی‌سازی» (Randomization) برای سریع‌تر شدن استفاده می‌کنند.

در این حالت زمان اجرای مورد نظر سریع‌تر از زمان اجرای بدترین حالت است. این الگوریتم‌ها با استفاده از روش تجزیه و تحلیل تصادفی تحلیل می‌شوند. نمونه‌هایی از این نوع الگوریتم‌ها شامل «مرتب سازی سریع تصادفی» (Randomized Quick Sort)، «انتخاب سریع» (Quick Select) و الگوریتم یا تابع «درهم‌سازی» (Hashing) می‌شوند. در ادامه مطلب «تحلیل سرشکن در طراحی الگوریتم»، قبل از پرداختن به روش تحلیل تجمعی در طراحی الگوریتم، مجموعه آموزش‌های مهندسی و علوم کامپیوتر تم آف به علاقه‌مندان معرفی می‌شوند.

معرفی فیلم های آموزش مهندسی و علوم کامپیوتر تم آف

دوره‌های آموزشی در پلتفرم تم آف بر اساس موضوع در قالب مجموعه‌های آموزشی مختلفی دسته‌بندی شده‌اند. یکی از این مجموعه‌ها مربوط به آموزش مهندسی و علوم کامپیوتر است که جهت آشنایی علاقه‌مندان و دانشجویان با این مجموعه آموزشی در این بخش معرفی می‌شود. دوره‌های متفاوتی پیرامون آموزش دروس علوم و مهندسی کامپیوتر در این مجموعه در دسترس قرار دارند. در ادامه، برخی از دوره‌های این مجموعه به طور مختصر معرفی شده‌‌اند:

• فیلم آموزش طراحی الگوریتم (طول مدت: ۱۵ ساعت و ۱۲ دقیقه، مدرس: دکتر فرشید شیرافکن): در این دوره آموزشی درس طراحی الگوریتم به دانشجویان و علاقه‌مندان آموزش داده می‌شود. درس طراحی الگوریتم، یکی از دروس مهم رشته مهندسی کامپیوتر در مقطع کارشناسی به حساب می‌آید که یادگیری آن نسبتا سخت است. برای مشاهده فیلم آموزش طراحی الگوریتم + کلیک کنید.
• فیلم آموزش ساختمان داده ها (طول مدت: ۱۰ ساعت و ۲۸ دقیقه، مدرس دکتر فرشید شیرافکن): ساختمان داده‌ها، یکی از دروس مهم و پایه‌ای دانشگاهی است و به عنوان مبحثی که نکات فراوانی دارد، در کنکور کارشناسی ارشد کامپیوتر و دکتری هوش مصنوعی و نرم افزار از دروس با ضریب بالا به شمار می‌رود. در این تم آف ساختمان داده‌ها به طور جامع آموزش داده شده است. برای مشاهده فیلم آموزش ساختمان داده ها + کلیک کنید.
• فیلم آموزش نظریه زبان ها و ماشین ها (طول مدت: ۸ ساعت و ۴۸ دقیقه، مدرس: دکتر فرشید شیرافکن): در این تم آف دانشجویان با سه موضوع «زبان»، «گرامر» و «ماشین» آشنا می‌شوند. این درس پیش‌نیاز درس طراحی کامپایلر است. با یادگیری زبان‌ها و گرامرها می‌توان نحوه کار کامپایلر و همچنین طراحی زبان‌های برنامه‌سازی را متوجه شد. برای مشاهده فیلم آموزش نظریه زبان‌ها و ماشین‌ها + کلیک کنید.
• فیلم آموزش نظریه زبان ها و ماشین – مرور و تست کنکور ارشد (طول مدت: ۸ ساعت و ۲۰ دقیقه، مدرس: دکتر فرشید شیرافکن): در این دوره آموزشی ابتدا مفاهیم عبارت منظم، زبان منظم، گرامر و ماشین متناهی تدریس شده است و سپس تست‌های مربوط به این مفاهیم بررسی شده‌اند. برای مشاهده فیلم آموزش نظریه زبان‌ها و ماشین – مرور و تست کنکور ارشد + کلیک کنید.
• فیلم آموزش طراحی و پیاده سازی زبان های برنامه سازی (طول مدت: ۱۰ ساعت و ۳۱ دقیقه، مدرس: دکتر فرشید شیرافکن): در این تم آف نحوه طراحی و پیاده‌سازی انواع داده‌ها، دستورات و ساختمان داده‌ها در چند زبان برنامه نویسی بررسی شده‌اند و امتیازها و معایب آن‌ها مقایسه شده است. برای مشاهده فیلم آموزش طراحی و پیاده‌سازی زبان‌های برنامه‌سازی + کلیک کنید.
• آموزش طراحی کامپایلر (طول مدت: ۱۴ ساعت و ۵۴ دقیقه، مدرس: منوچهر بابایی): این دوره آموزشی برای دانشجویان و علاقه‌مندان به طراحی کامپایلر مناسب است. همچنین این درس یکی از دروس مهم رشته کامپیوتر در مقطع کارشناسی به حساب می‌آید. برای مشاهده فیلم آموزش طراحی کامپایلر + کلیک کنید.

حال پس از معرفی مجموعه آموزش‌های مهندسی و علوم کامپیوتر، در بخش بعدی از مطلب «تحلیل سرشکن در طراحی الگوریتم» روش تحلیل تجمعی در طراحی الگوریتم را یاد می‌گیریم.

تحلیل تجمعی در سرشکن چیست؟

«تحلیل تجمعی» (Aggregate Analysis) در سرشکن دارای دو مرحله است که این مراحل در ادامه ارائه شده‌اند:

• در مرحله اول باید نشان داد که دنباله‌ای از n

   عملیات، زمانی برابر با $$T(n)$$ را در بدترین حالت دارند.

• سپس در مرحله بعدی، نشان داده می‌شود که به طور متوسط هر عمل دارای پیچیدگی زمانی برابر با $$frac {T(n)} {n}$$ است. بنابراین در تحلیل تجمعی هر عمل هزینه یکسانی دارد. دقیقاً مانند مثال قبلی که درباره پختن کیک بود و هر دو عملیات به جای سریع یا آهسته بودن، متوسط در نظر گرفته شدند.

به عنوان یک مثال رایج از روش تحلیل تجمعی می‌توان به «پشته اصلاح شده» (Modified Stack) اشاره کرد. پشته‌ها ساختمان داده‌های خطی هستند که دو عملیات در زمان ثابت دارند. این رویکردهای پشته در برنامه نویسی در ادامه شرح داده شده‌اند:

• یکی از رویکردها استفاده از push(element)

   است که «عنصر» (Element) را در بالای پشته قرار می‌دهد.

• رویکرد بعدی pop()

   است که عنصر بالایی را از پشته خارج می‌کند و آن را برمی‌گرداند.

هر دو عملیات فوق دارای زمان ثابتی هستند، بنابراین، کل n

 عملیات با هر ترتیبی، نتایجی با زمان $$O(n)$$ دارند. در ادامه مثالی از روش استفاده پشته در برنامه نویسی ارائه شده است که در آن یک عملیات جدید به پشته اضافه می‌شود. در این کدها تابع multipop(k)

 عنصر k

 را از پشته خارج یا همان Pop می‌کند یا اگر قبل از آن همه عناصر تمام شوند، آن‌ها را از پشته خارج می‌کند و پشته متوقف می‌شود.

multipop(k):
while stack not empty and k > 0:
k = k - 1
stack.pop()

با بررسی «شبه کد» (pseudo-code) فوق، به راحتی می‌توان مشاهده کرد که این عملیات دارای زمان ثابت نیستند. تابع multipop

 می‌تواند حداکثر n

 بار اجرا شود. n

 نیز اندازه یا همان سایز پشته در نظر گرفته می‌شود. بنابراین می‌توان گفت که بدترین زمان اجرا برای تابع multipop

 مقدار $$O(n)$$ است. در نتیجه، در تجزیه و تحلیل‌های غیر معمول، تعداد n

 عملیات multipop

 زمانی برابر با $$O(n^2)$$ صرف می‌کند. با این حال، در واقع اینطور نیست. وقتی multipop

 بیشتر بررسی می‌شود، این موضوع مشاهده خواهد شد که multipop

 چون چیزی برای Pop یا خارج کردن ندارد، بدون وارد کردن یا Push عناصر نمی‌تواند کاری انجام دهد.

در حقیقت هر دنباله‌ای از n

 عملیات multipop

 ، pop

 و push

 می‌تواند حداکثر $$O(n)$$ زمان ببرد. multipop

 تنها عملیات زمان غیر ثابت در این پشته است و فقط وقتی زمانی برابر با $$O(n)$$ دارد که n

 عملیات Push زمان ثابت در پشته وجود داشته باشد. در بدترین حالت، عملیات زمان ثابت وجود دارند و فقط یکی از آن‌ها دارای زمان $$O(n)$$ است. برای هر مقدار از n

 ، هر دنباله‌ای از multipop

 ، pop

 و push

 زمانی برابر با $$O(n)$$ دارد. بنابراین، استفاده از تحلیل تجمعی دارای رابطه زیر است:

در نهایت می‌توان گفت که این پشته دارای هزینه سرشکنی $$O(1)$$ برای هر عملیات است. در ادامه بررسی تحلیل سرشکن در طراحی الگوریتم روش حسابرسی را بررسی می‌کنیم.

روش حسابرسی برای تحلیل سرشکن در طراحی الگوریتم چیست؟

به دلیل این‌که «روش حسابرسی» (Accounting Method) ایده‌ها و اصطلاحاتش را از روش‌های حسابداری دریافت می‌کند، با این نام، نام‌گذاری شده است. در این روش هر عملیاتی که «انجام یا شارژ می‌شود» (Charge)، هزینه سرکشن نام دارد. برخی از عملیات را می‌توان بیشتر یا کمتر از هزینه واقعی آن‌ها انجام داد و شارژ کرد. اگر هزینه سرشکن در طراحی الگوریتم یک عمل از هزینه واقعی آن بیشتر شود، تفاوت این دو مورد، «اعتبار» (Credit) نامیده می‌شود و این تفاوت به اشیا خاصی در ساختمان داده یا الگوریتم اختصاص داده خواهد شد. اعتبار را می‌توان بعداً برای کمک به پرداخت سایر عملیاتی نیز استفاده کرد که هزینه سرشکن شده آن‌ها کمتر از هزینه واقعی آن‌ها است.

همچنین، اعتبار هرگز نمی‌تواند در هیچ دنباله‌ای از عملیات منفی باشد. هزینه سرشکنی یک عمل بین هزینه واقعی عمل و اعتباری تقسیم می‌شود که یا سپرده یا تمام شده است. هر عملیات بر خلاف تجزیه و تحلیل تجمعی می‌تواند هزینه سرشکن در طراحی الگوریتم متفاوتی داشته باشد. انتخاب هزینه سرشکن برای هر عمل مسئله مهمی به حساب می‌آید، اما هزینه‌ها باید همیشه برای هر عمل داده شده بدون توجه به دنباله‌ای از عملیات، یکسان باشد. این موضوع دقیقاً مانند هر روش تحلیل سرشکن در طراحی الگوریتم است. با نگاهی به پشته اصلاح شده از بخش پیشین، هزینه‌های عملیات مشخص به صورت زیر نشان داده می‌شوند:

Push: 1
Pop: 1
Multipop: min(stack.size, k)

اگر k

 کمتر از تعداد عنصرهای پشته باشد، هزینه تابع Multipop

اندازه سایز پشته یا همان k

 خواهد بود. با تخصیص هزینه‌های سرشکن به توابع، هزینه‌های زیر دریافت می‌شوند:

Push: 2
Pop: 0
Multipop: 0

در اینجا این موضوع قابل توجه است که هزینه سرشکن در طراحی الگوریتم برای تابع Multipop

 ثابت در نظر گرفته می‌شود، در حالی که هزینه واقعی آن متغیر است. در مرحله آخر این موضوع نشان داده می‌شود که «پرداخت» (Pay) برای هر دنباله‌ای از عملیات با استفاده از هزینه‌های سرشکن امکان‌پذیر است. انجام این مرحله با استفاده از پول، مفید خواهد بود، بنابراین یک دلار معادل یک هزینه می‌شود. اگر پشته‌ای به عنوان پشته‌ای واقعی از صفحات در نظر گرفته شود، این موضوع واضح‌تر خواهد شد. وارد یا Push کردن صفحه‌ای به پشته، عمل قرار دادن آن صفحه در بالای پشته است. Pop کردن صفحه نیز عمل خارج کردن صفحه بالایی پشته به حساب می‌آید.

بنابراین، هنگامی که در این مثال یک صفحه به پشته Push می‌شود، یک دلار برای هزینه واقعی عمل پرداخت خواهد شد و با یک دلار اعتبار تا این بخش مثال باقی خواهد ماند. این موضوع به این دلیل است که هزینه سرشکن در طراحی الگوریتم برای Push دریافت می‌شود و ۲ دلار است، سپس هزینه واقعی که یک دلار در نظر گرفته می‌شود از آن کم خواهد شد و یک دلار باقی می‌ماند. این یک دلار بالای صفحه Push شده قرار می‌گیرد. بنابراین، در هر نقطه از زمان، هر صفحه‌ای در پشته دارای یک دلار اعتبار بر روی آن است. یک دلار روی صفحه بالایی پشته به عنوان پول مورد نیاز برای Pop کردن صفحه وجود دارد.

برای خارج یا Pop کردن صفحه نیز به یک دلار نیاز است؛ زیرا هزینه سرشکن Pop کردن، یعنی صفر دلار از هزینه واقعی Pop کردن یعنی یک دلار کم می‌شود. در هر نقطه از زمان، هر صفحه دقیقاً یک دلار روی خود دارد که می‌توان از آن برای Pop کردن پشته استفاده کرد. تابع Multipop

 از pop

 به عنوان یک «برنامه فرعی یا زیر روتین» (Subroutine) استفاده می‌کند. فراخوانی Multipop

 در پشته هزینه‌ای ندارد، اما pop

 در آن از یک دلار روی هر صفحه برای حذف صفحه استفاده خواهد کرد. از آن‌جایی که همیشه یک دلار روی هر صفحه در پشته وجود دارد، اعتبار هرگز منفی نخواهد بود.

به طور کلی، این همان ایده‌ای به حساب می‌آید که در روش تحلیل تجمعی نیز مورد بررسی قرار گرفت. اجرای Multipop

 یا pop

 تا زمانی معنی ندارد که چیزی به پشته Push نشده باشد؛ زیرا چیزی برای Pop کردن وجود ندارد. بنابراین، بدترین هزینه n

 عملیات با $$O(n)$$ برابر است. در ادامه مطلب «تحلیل سرشکن در طراحی الگوریتم» روش پتانسیل را یاد می‌گیریم.

روش پتانسیل برای تحلیل سرشکن در طراحی الگوریتم چیست ؟

«روش پتانسیل» (Potential Method) شباهت بسیاری با روش حسابرسی دارد. با این حال، به جای این‌که تجزیه و تحلیلی درباره هزینه و اعتبار داشته باشد، به وظایفی می‌پردازد که قبلاً انجام شده‌اند و به عنوان انرژی پتانسیلی در نظر گرفته می‌شوند که می‌توانند هزینه عملیات بعدی را بپردازند. این موضوع شبیه به غلتیدن یک سنگ از بالای تپه به پایین است که انرژی پتانسیلی ایجاد می‌کند و می‌تواند سنگ را بدون هیچ تلاشی از پایین تپه مجدداً به بالا بازگرداند. با این حال، برخلاف روش حسابرسی، به طور کلی، انرژی پتانسیل با ساختمان داده ارتباط دارد و ارتباطی با عملیات فردی نخواهد داشت. روش پتانسیل به صورت زیر عمل می‌کند:

• با یک ساختمان داده اولیه به نام $$D_{0}$$ شروع می‌شود.
• سپس در این مرحله n

   عملیات انجام می‌شود و ساختمان داده اولیه به $$D_{1}، D_{2}، D_{3}،…، D_{n}$$ تبدیل می‌شود.

• $$c_{i}$$ هزینه مرتبط با i

   امین عملیات خواهد بود.

• $$D_{i}$$ نتیجه نهایی ساختمان داده برای i

   امین عملیات است.

Φ نشان‌دهنده تابع پتانسیلی است که ساختمان داده D را به عدد $$Φ(D)$$ نگاشت می‌کند، پتانسیل با ساختمان داده ارتباط دارد. هزینه سرشکن در طراحی الگوریتم عملیات i

 با فرمول زیر برابر است:

$$a_{i} = c_{i} + Φ (D_{i}) – Φ(D_{i-1})$$

بنابراین، این معادله بدان معنی است که برای بیش از n

 عملیات، هزینه سرشکن در طراحی الگوریتم برابر با رابطه زیر است:

$$sum_{i-1} ^n a_{i}=sum_ {i-1} ^n (c_{i} + Φ (D_{i}) – Φ(D_{i-1}))$$

به دلیل اینکه این «مجموع به صورت تلسکوپی» (Telescoping Sum) است، بنابراین با رابطه زیر برابر می‌شود:

$$sum_{i-1} ^n c_{i} + Φ (D_{n}) – Φ(D_{0})$$

در این روش، نیاز است که برای همه i

 ها جهت اثبات این‌که هزینه سرشکن در طراحی الگوریتم n

 عملیات، به اندازه یک کران بالا بیشتر از هزینه کل واقعی باشد، $$ Φ (D_{i}) geq Φ(D_{0})$$ در نظر گرفته شود. روش رایج برای انجام این کار تعریف $$ Φ(D_{0}) = 0$$ و نشان دادن $$ Φ (D_{i}) geq 0$$ است.

در طول دنباله عملیات، i

 امین عمل تفاوت پتانسیلی $$ Φ (D_{i}) – Φ(D_{i-1})$$ دارد. اگر این مقدار مثبت شود، سپس هزینه سرشکن در طراحی الگوریتم $$ a_{i}$$ «شارژ زیادی» (Overcharge) برای این عملیات خواهد داشت و انرژی پتانسیل الگوریتم را افزایش می‌دهد. اگر این مقدار منفی باشد، حالت «شارژ کم» (Undercharge) به وجود می‌آید و انرژی پتانسیل الگوریتم کاهش می‌یابد.

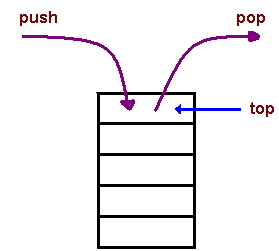
اگر مثال پشته اصلاح شده در نظر گرفته شود. به سادگی می‌توان گفت تابع پتانسیل انتخاب شده، تعداد آیتم‌های «بالای» (Top) پشته خواهد بود. بنابراین، قبل از شروع دنباله عملیات، $$ Φ(D_{0}) = 0$$ برقرار است؛ زیرا هیچ آیتمی در پشته وجود ندارد. برای همه عملیات بعدی، مشخص است که $$ Φ (D_{i}) geq 0$$ برقرار خواهد بود؛ زیرا نمی‌توان تعداد موارد منفی در پشته داشت. جهت محاسبه پتانسیل تفاوت برای عملیات Push، رابطه زیر استفاده می‌شود:

$$Φ (D_{i}) – Φ(D_{i-1}) = (stack.size +1 )− stack.size =1$$

بنابراین، هزینه سرشکن در طراحی الگوریتم برای عملیات Push به صورت زیر است:

$$a_{i} = c_{i} + Φ (D_{i}) – Φ(D_{i-1}) = 1 + 1 = 2$$

به طور کلی همه این عملیات دارای هزینه سرشکن در طراحی الگوریتم $$O(1)$$ هستند، بنابراین، هر دنباله‌ای از عملیات به طول n

 $$O(n)$$ زمان می‌برد. از آن‌جایی که ثابت شد که برای همه i‌

ها $$ Φ (D_{i}) geq Φ(D_{0})$$ است، این رابطه یک کران بالا واقعی به حساب می‌آید. همچنین، زمان بدترین حالت از n

 عملیات برابر با $$O(1)$$ است. در ادامه مطلب «تحلیل سرشکن در طراحی الگوریتم» تحلیل سرشکن در عمل درج الگوریتم «درخت قرمز سیاه» (Red-Black Tree) را یاد می‌گیریم.

تحلیل سرشکن در عمل درج الگوریتم درخت قرمز سیاه چگونه است؟

در ابتدا، تحلیل سرشکن عمل درج در درخت قرمز سیاه با استفاده از روش پتانسیل یا «فیزیک‌دان» (Physicist) بررسی می‌شود. در استفاده از روش پتانسیل، یک تابع پتانسیل با نام Φ تعریف شده است که ساختمان داده را به یک مقدار واقعی غیر منفی نگاشت می‌کند. یک عمل می‌تواند منجر به تغییر این پتانسیل شود. تابع پتانسیل Φ با روش زیر تعریف می‌شود.

در تابع فوق، n

 «گره‌ای» (Node) درخت قرمز سیاه به حساب می‌آید. تابع پتانسیل $$Φ = sum {g(n)}$$ برای همه گره‌های درخت قرمز سیاه عمل می‌کند. علاوه بر این، زمان سرشکن یک عمل به صورت زیر تعریف می‌شود:

$$Amortized time = c + Delta phi (h)$$

$$ Delta phi (h)= phi (h’) – phi (h) $$

در فرمول‌های فوق، h

 و h’

 به ترتیب حالت درخت قرمز سیاه را قبل و بعد از عملیات نشان می‌دهند. c

 نیز نشان‌دهنده هزینه واقعی عمل است. به این نکته نیز باید توجه داشت که تغییر پتانسیل باید برای‌ عملیات کم هزینه، مثبت و برای عملیات پرهزینه، منفی باشد. در ادامه یک گره جدید در یکی از «برگ‌های» (Leaf) درخت قرمز سیاه درج می‌شود. برگ‌های درخت قرمز سیاه با انواع مختلف در تصویر زیر نمایش داده شده است:

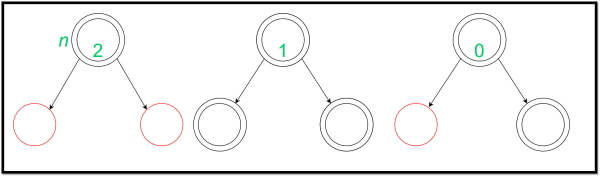
درج‌ها و تجزیه و تحلیل‌های سرشکن در طراحی الگوریتم به صورت زیر نمایش داده می‌شوند. در ادامه، تصویر اولین عملیات نمایش داده شده است:

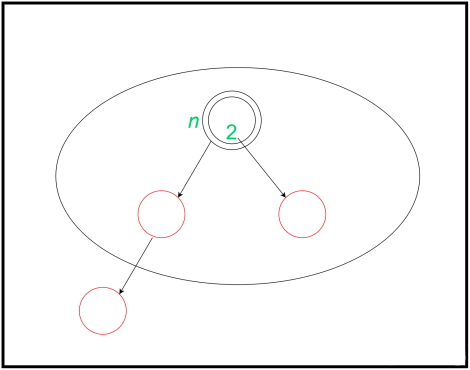
این درج با رنگ‌آمیزی مجدد والد و دیگر خواهر و برادرهای گره انجام می‌شود که به رنگ قرمز هستند. سپس، پدربزرگ و عموی آن گره برگ برای رنگ‌آمیزی بعدی در نظر گرفته می‌شوند که منجر به ایجاد هزینه سرشکن در طراحی الگوریتم ۱- شده است. این اتفاق زمانی رخ می‌دهد که پدربزرگ گره برگ قرمز باشد. گاهی اوقات هزینه سرشکن این گره ۲- می‌شود و این موضوع زمانی اتفاق می‌افتد که عمو و پدربزرگ برگ سیاه باشند. همچنین گاهی این هزینه عدد ۱ می‌شود و این موضوع زمانی رخ می‌دهد که عموی برگ، قرمز و پدربزرگ برگ، سیاه هستند. این درج به صورت زیر نمایش داده شده است:

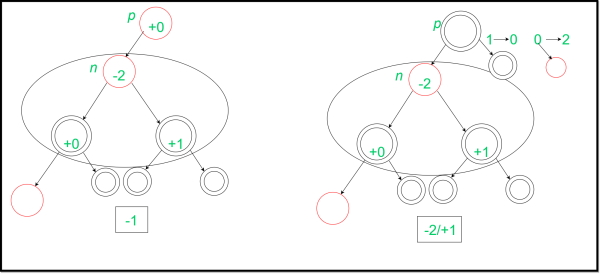
درج دیگری در ادامه مشاهده می‌شود که در ابتدا تصویر این درج ارائه شده است:

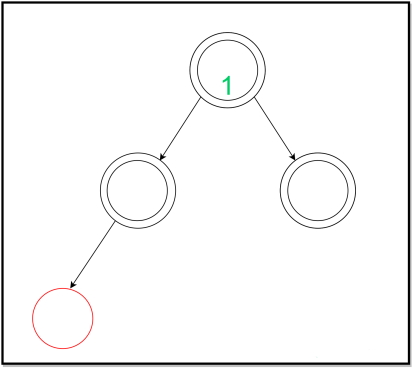
در درج انجام شده در تصویر درخت فوق، گره بدون هیچ تغییری درج می‌شود و برگ‌ها در عمق‌های قبلی به رنگ سیاه باقی می‌مانند. این مورد زمانی رخ می‌دهد که برگ دارای یک «خواهر یا برادر سیاه رنگ» (Black Sibling) یا بدون هیچ خواهر یا برادری باشد. در این الگوریتم باید به این نکته نیز توجه داشت که رنگ گره «تهی» (Null)، سیاه در نظر گرفته می‌شود. بنابراین، هزینه سرشکنی این درج صفر است. در ادامه درج دیگری مشاهده می‌شود:

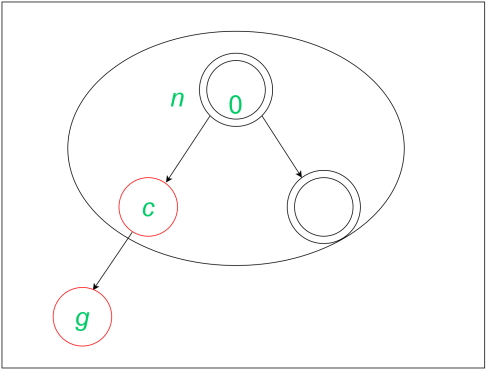
در درج فوق برای الگوریتم قرمز و سیاه، نمی‌توان گره برگ، والد، خواهر و برادر آن را دوباره رنگ‌آمیزی کرد تا عمق گره سیاه مانند قبل باقی بماند. بنابراین، باید چرخش «چپ به چپ» (Left – Left) انجام شود. بعد از این چرخش، اگر پدربزرگ گره g

 یا همان گره درج شده جدید سیاه باشد، هیچ تغییری ایجاد نمی‌شود. همچنین، هنگامی که پدربزرگ گره جدید g

 قرمز رنگ باشد، هیچ تغییری به وجود نخواهد آمد. بنابراین، هزینه سرشکن در طراحی الگوریتم کل برای این درج‌ها برابر با عدد ۲ است. در ادامه تصویری از کل درج نشان داده می‌شود:

پس از محاسبه این هزینه‌های سرشکنی خاص برای هر برگ درخت قرمز سیاه، می‌توان کل هزینه سرشکنی درج در این درخت را محاسبه کرد. از آن‌جایی که ممکن است دو گره قرمز دارای رابطه والد و فرزندی تا ریشه درخت قرمز سیاه باشند. بنابراین، برای گسترش درخت (حالت گوشه یا همان Corner)، تعداد گره‌های سیاه با دو فرزند قرمز با هزینه سرشکنی برابر با عدد یک کاهش می‌یابند و بیشترین افزایش تعداد گره‌های سیاه بدون فرزندان قرمز با هزینه سرشکنی یک مشخص می‌شود. تابع پتانسیل حداکثر هزینه‌ای برابر با عدد یک برای خطا درج برگ در نظر می‌گیرد. از آن‌جایی که برای هر عمل یک واحد پتانسیل هزینه می‌شود، بنابراین رابطه زیر ارائه شده است:

$$Delta phi (h) leq n$$

در رابطه فوق، n

 تعداد کل گره‌ها را نشان می‌دهد. سپس، هزینه سرشکن در طراحی الگوریتم کل برای عملیات درج در درخت قرمز سیاه $$O(n)$$ می‌شود.

جمع‌بندی

تحلیل سرشکن در طراحی الگوریتم، رویکردی برای تجزیه و تحلیل هزینه ساختمان داده و الگوریتمی است که میانگین بدترین هزینه عملیات در طول زمان را نشان می‌دهند و این حالت عملیات مهمی از الگوریتم را نشان می‌دهد. در این مطلب سعی شد به طور جامع همه بخش‌های تحلیل سرشکن در طراحی الگوریتم بررسی شود. تحلیل سرشکن در طراحی الگوریتم دارای روش‌های تحلیل تجمعی، روش حسابرسی و روش پتانسیل است که همه این موارد با مثالی از درج و حذف در پشته توضیح داده شده‌اند. در نهایت، برای درک بهتر این موضوع، سرشکن در ساختمان داده‌های آرایه، پشته و درخت قرمز سیاه برای عملیات درج شرح داده شد. دوره‌های آموزشی نیز در ارتباط به الگوریتم‌ها و ساختمان داده برای یادگیری بیشتر علاقه‌مندان در این مطلب ارائه شده‌اند.