مسئله تانک آلمانی – آشنایی و پیاده سازی در پایتون

مسئله تانک آلمانی، مسئلهای معروف در نظریه احتمال است که نحوه تخمین اندازه کل جمعیت بر اساس نمونههای محدود را نمایش میدهد. در این مقاله از مجله تم آف، به معرفی مسئله تانک آلمانی و آموزش نحوه پیادهسازی آن در پایتون به صورت گام به گام خواهیم پرداخت.

تاریخچه مسئله تانک آلمانی
در طول جنگ جهانی دوم، آلمان در حال تولید تانکهایی همچون پنتر (Panther) بودند که برای کشورهای متفقین مشکلساز بود. کشورهای متّفق به دنبال راهی برای تخمین تعداد تانکهای تولیدی توسط آلمان بودند.

آنها از برترین ماموران اطلاعاتی به این منظور کمک میگرفتند اما در کنار این راهحل، از کارشناسان آمار (Statistician) نیز کمک خواستند. هر دو دسته با توجه به اطلاعاتی که به دست آورده بودند، پیشبینیهایی برای تعداد تانکهای تولید شده در هر ماه ارائه کردند که به شرح زیر است:
| تاریخ | پیشبینی مامورین اطلاعات | پیشبینی کارشناسان آمار |
| ژوئن ۱۹۴۰ | ۱۰۰۰ | ۱۶۹ |
| ژوئن ۱۹۴۱ | ۱۵۵۰ | ۲۴۴ |
| آگوست ۱۹۴۲ | ۱۵۵۰ | ۳۲۷ |
همانطور که مشاهده میکنیم، به صورت میانگین کارشناسان آمار مقادیر ۸۰٪ پایینتر را پیشبینی کردهاند که اختلاف بسیار بزرگی است. پس از اتمام جنگ و بررسی اسناد مربوط به تولید، اعداد واقعی مربوط به تولید زمانهای گفته شده به شکل زیر آمده است:
| تاریخ | پیشبینی مامورین اطلاعات | پیشبینی کارشناسان آمار | مقادیر واقعی |
| ژوئن ۱۹۴۰ | ۱۰۰۰ | ۱۶۹ | ۱۲۲ |
| ژوئن ۱۹۴۱ | ۱۵۵۰ | ۲۴۴ | ۲۷۱ |
| آگوست ۱۹۴۲ | ۱۵۵۰ | ۳۲۷ | ۳۴۲ |
رابطه قدر مطلق درصد خطا (Absolute Percentage Error یا APE) به شکل زیر است:
$$ APE = 100 times left | frac { y – P }{ y } right | $$
اگر از این رابطه برای محاسبه میانگین قدر مطلق درصد خطا استفاده کنیم، برای ماموران اطلاعات عدد ۵۱۴/۹% و برای کارشناسان آمار عدد ۱۷/۶% به دست خواهد آمد. به این ترتیب مشاهده میکنیم که چه مقدار ماموران اطلاعات متفقین دچار خطا شده بودهاند و همان اندازه کارشناسان آمار دقت خوبی از خود نشان دادهاند.
کارشناسان آمار چگونه توانستد تا این حد پیشبینی دقیقی داشته باشند؟
کارشناسان آمار، برخلاف ماموران اطلاعات که به دنبال نشت اطلاعات و جاسوسی از کارخانجات آلمانی بودند، از اطلاعات موجود در صحنه نبرد استفاده کردند. آنها متوجه شده بودند که شرکتهای سازنده تانک، بر روی قطعات تانکها یک شماره سریال (Serial Number) مینویسند که این اعداد به ترتیب (مانند ۴۰۳، ۴۰۴، ۴۰۵، …) هستند. نکته مهمی که آلمانیها به آن توجه نکرده بودند، مرتب بودن این اعداد بود.

کارشناسان آمار با جمعآوری شماره سریال تانکهای منهدم شده، ترک شده، مستهلک و یا غنیمت گرفته شده، به مجموعهای از شماره سریالها دست یافتد. آنها پس از انجام برخی تحلیلها به این نتیجه رسیده بودند که اگر شماره سریال تعداد مشخصی تانک را داشته باشند، میتواند با فرمول زیر تعداد واقعی آنها را با دقت خوبی پیشبینی کنند.
$$ N cong m + frac { m } { k } – 1 $$
در این رابطه، متغیر N تعداد واقعی تانکها، m بزرگترین شماره سریال یافته شده و k تعداد شماره سریالهای یافت شده است. برای مثال اگر شماره سریالهای زیر یافته شده باشد:
$$ 5, ; 19, ; 29, ; 31 ; 55 ; 60 $$
مقدار m برابر با بزرگترین عدد یافت شده یعنی ۶۰ خواهد بود و مقدار k برابر با ۶ خواهد بود. در این شرایط رابطه فوق به صورت زیر پیشبینی انجام میدهد:
$$
N cong m + frac { m } { k } – 1 = 60 + frac { 60 } { 6 } – 1 = 60 + 10 – 1 = 69
$$
به این ترتیب میتوانیم با اطمینان زیادی بگوییم بیشترین شماره سریال موجود عددی نزدیک به ۶۹ است.
رابطه گفته شده چگونه کار میکند؟
فرض میکنیم که شماره سریالهای یافت شده به شکل زیر است:
$$ x _ 1 , x _ 2 , ; … ; , x _ k $$
اگر این اعداد مرتب شده باشند، ابتدای بازه را ۱ و انتهای آن را N در نظر بگیریم، اختلاف هر شماره سریال از شماره سریال قبلی به شکل زیر خواهد بود:
$$
1 to x _ 1 to x _ 2to ;…;to x _ 3to N
$$
$$
begin{aligned}
& d_1=x_1-1 \
& d_2=x_2-x_1-1 \
& d_3=x_3-x_2-1 \
& vdots \
& d_k=x_k-x_{k-1}-1
end{aligned}
$$
توجه داشته باشید که اختلاف بین ۱ (کمترین مقدار قابل مشاهده) و $$ x _ 1 $$ را نیز به عنوان اولین فاصله در نظر میگیریم. حال میتوانیم امید ریاضی (Expected Value) d را که بازه بین هر دو داده متوالی است را محاسبه کنیم:
$$
begin{aligned}
mathrm{E}[d]=mathrm{E}left[d_i midright. & 1 leq i leq k] \
& =frac{left(x_1-1right)+left(x_2-x_1-1right)+left(x_3-x_2-1right)+cdots+left(x_k-x_{k-1}-1right)}{k-1} \
& =frac{x_1-1+x_2-x_1-1+x_3-x_2-1+cdots+x_k-x_{k-1}-1}{k} \
& =frac{x_k-k}{k}=frac{x_k}{k}-1
end{aligned}
$$
بنابراین، میتوان گفت بین هر شماره سریال با شماره سریال بعدی، به صورت میانگین $$ frac { x _ k } { k } – 1 $$ واحد فاصله وجود دارد. حال میتوانیم امید ریاضی اختلاف N با $$ x _ k $$ را نیز محاسبه کنیم:
$$
mathrm{E}left[N-x_kright]=frac{x_k}{k}-1 rightarrow mathrm{E}[N]=x_k+frac{x_k}{k}-1
$$
حال با جایگذاری مقدار m به جای $$ x _ k $$ و استفاده از N به جای امید ریاضی N خواهیم داشت:
$$
mathrm{E}[N] cong N cong m+frac{m}{k}-1=x_k+frac{x_k}{k}-1
$$
به این ترتیب رابطه گفته شده اثبات میشود.
اثبات رابطه با کمک امید ریاضی M
امید ریاضی هر توزیع به شکل زیر قابل محاسبه است:
$$
mathrm{E}[X]=x_1 cdot p_1+x_2 cdot p_2+cdots+x_k cdot p_k=sum_{i=1}^k x_i cdot p_i
$$
به عبارتی، هر مقدار از توزیع، در احتمال وقوع خود ضرب میشود و در نهایت اعداد حاصل با یکدیگر جمع میشود. اگر جامعه آماری اولیه به شکل زیر باشد:
$$
{ 1,;2,;3,;…,; N – 1 , ; N}
$$
امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها
در این شرایط اگر k عدد نمونهبرداری انجام دهیم، به تعداد $$ left (_k ^ N right) $$ حالت برای نمونهبرداری وجود خواهد داشت. حال اگر بخواهیم بزرگترین نمونه انتخاب شده برابر با m باشد، باید $$ k – 1 $$ نمونه دیگر را از بازه $$ [ 1,; m – 1 ] $$انتخاب کنیم:
$$
P_{(M=m)}=frac{left(begin{array}{l}
m-1 \
k-1
end{array}right)}{left(begin{array}{l}
N \
k
end{array}right)}
$$
به این ترتیب احتمال بیشینه بودن هر مقدار m قابل محاسبه خواهد بود. حال میتوانیم تابع توزیع احتمال را وارد رابطه امید ریاضی کنیم:
$$
begin{array}{rl}
mathrm{E}[M]:=sum_{m=k}^N & m cdot P_{(M=m)}=sum_{m=k}^N m cdot frac{left(begin{array}{l}
m-1 \
k-1
end{array}right)}{left(begin{array}{l}
N \
k
end{array}right)} \
& =sum_{m=k}^N m cdot frac{frac{(m-1) !}{(k-1) ! cdot(m-k) !}}{N !}=sum_{m=k}^N m cdot frac{(m-1) ! cdot k ! cdot(N-k) !}{N ! cdot(k-1) ! cdot(m-k) !} \
& =sum_{m=k}^N frac{k cdot m ! cdot k ! cdot(N-k) !}{N ! cdot k ! cdot(m-k) !}=frac{k cdot k ! cdot(N-k) !}{N !} cdot sum_{m=k}^Nleft(begin{array}{l}
m \
k
end{array}right) \
& =frac{k cdot k ! cdot(N-k) !}{N !} cdotleft(begin{array}{l}
N+1 \
k+1
end{array}right)=frac{k cdot k ! cdot(N-k) !}{N !} cdot frac{(N+1) !}{(k+1) ! cdot(N-k) !} \
& =frac{k cdot(N+1)}{(k+1)}
end{array}
$$
پس از این مراحل، طرف دو معادله به خوبی ساده میشود. حال میتوانیم بگوییم:
$$
begin{aligned}
& mathrm{E}[M]=frac{k cdot(N+1)}{(k+1)} \
& rightarrow(k+1) cdot mathrm{E}[M]=k cdot(N+1) \
& rightarrow N+1=frac{(k+1) cdot mathrm{E}[M]}{k} \
& rightarrow N=frac{k cdot mathrm{E}[M]+mathrm{E}[M]}{k}-1=mathrm{E}[M]+frac{mathrm{E}[M]}{k}-1
end{aligned}
$$
با توجه به اینکه مقدار مشاهده از توزیع M برای ما برابر با m است، آن را به عنوان بهترین حدس در رابطه قرار میدهیم:
$$
to N = m + frac { m }{ k } – 1
$$
به این ترتیب در این شرایط نیز رابطه گفته شده حاصل میشود و میدانیم که رابطه گفته شده به چه شکل حاصل شده است.
پیادهسازی مسئله تانک آلمانی در پایتون
تمامی کدهای نوشته شده برای این مطلب در محیط برنامهنویسی پایتون، از طریق این لینک در دسترس است.
- برای دانلود فایل حاوی کدهای پایتون + اینجا کلیک کنید.
ساخت مجموعه داده برای مسئله تانک آلمانی
در ابتدا، برای بررسی دقت مدلهای (Model) یادگیری ماشین (Machine Learning) و روش آماری آورده شده، به یک مجموعه داده (Dataset) نیاز داریم که به اندازه کافی بزرگ باشد. به این منظور یک مجموعه داده سنتز خواهیم کرد.
در ابتدا کتابخانههای مورد نیاز پایتون را فراخوانی میکنیم:
import numpy as np
import pandas as pd
import seaborn as sb
import sklearn.metrics as met
import matplotlib.pyplot as plt
import sklearn.linear_model as lm
import sklearn.preprocessing as ppاین موارد به ترتیب برای عملیات زیر استفاده خواهند شد:
- کتابخانه Numpy
برای کار با داده، ماتریس و محاسبات آماری استفاده خواهد شد.
- کتابخانه Pandas
برای تولید و ذخیرهسازی مجموعه داده استفاده خواهد شد.
- کتابخانه Seaborn
برای رسم نمودار همبستگی بین ویژگیهای مجموعه داده استفاده خواهد شد.
- بخش metrics
مربوط به کتابخانه Scikit-learn
برای محاسبه معیارهای ارزیابی رگرسیون (Regression Metrics) کاربرد خواهد داشت. برای آشنایی با معیارهای ارزیابی رگرسیون در پایتون، میتوانید به مطلب «بررسی معیارهای ارزیابی رگرسیون در پایتون – پیاده سازی + کدها» مراجعه نمایید.
- کتابخانه Matplotlib
برای رسم نمودارهای تحلیل داده و رگرسیون کاربرد خواهد داشت.
- بخش linear_model
مربوط به کتابخانه Scikit-learn
برای ایجاد و آموزش مدل رگرسیون خطی (Linear Regression) کاربرد خواهد داشت.
- بخش preprocessing
مربوط به کتابخانه Scikit-learn
برای اصلاح مقیاس (Rescaling) مجموعه داده استفاده خواهد شد.
رسم نمودار در پایتون با Matplotlib — راهنمای کاربردی
تنظیمات مربوط به Random State و Style کدها برای مسئله تانک آلمانی
قبل از شروع کدنویسی، دو سطر زیر را وارد میکنیم:
np.random.seed(seed=0)
plt.style.use(style='ggplot')در نتیجه این دو سطر کد، اعداد تصادفی تولید شده و در نتیجهی آن خروجیهای کد قابل بازتولید (Reproducible) خواهند بود و نمودارهای Matplotlib
با فرمت ggplot
رسم خواهند شد.
تولید مجموعه داده برای مسئله تانک آلمانی
به منظور تولید مجموعه داده مربوط با مسئله گفته شده، تابعی به اسم CreateDataset
ایجاد میکنیم:
def CreateDataset(nD:int,
MinN:int,
MaxN:int,
MinK:int,
MaxK:int) -> pd.DataFrame:این تابع در ورودی موارد زیر را دریافت خواهد کرد:
- تعداد داده مورد نظر ( nD
): این عدد تعیین خواهد کرد که مجموعه داده دارای چند نمونه (Sample) باشد.
- کمترین مقدار N که با ورودی MinN
شناخته میشود.
- بیشترین مقدار N که با ورودی MaxN
شناخته میشود.
- کمترین مقدار k که با ورودی MinK
شناخته میشود.
- بیشترین مقدار k که با ورودی MaxK
شناخته میشود.
در خروجی تابع نیز یک دیتافریم (Dataframe) دریافت خواهیم کرد. به عبارت دیگر این تابع سناریوهای مختلف مربوط به شرایط جنگ جهانی دوم را شبیهسازی میکند و اعداد موجود را ذخیره میکند:
- به تعداد N عدد تانک با شماره سری 1 تا N تولید میکند.
- به تعداد k عدد تانک با شماره سریهای تصادفی $$ x _ 1 , x _ 2 , ; … ; , x _ k $$ به دست متفقین میافتد.
- معیارهای آماری توزیع x محاسبه و به همراه N و k به یک دیتافریم اضافه میشود.
- این شبیهسازی به تعداد nD
بار تکرار میشود.
- مقدار N به صورت تصادفی از بازه $$ left [ MinN,;MaxN right] $$ انتخاب میشود.
- مقدار k به صورت تصادفی از بازه $$ left [ MinN,;MaxN right] $$ انتخاب میشود.
به این ترتیب به جای 3 عدد داده مربوط به زمان جنگ جهانی، به تعداد نامحدودی نمونه داده میتوانیم تولید کنیم و روی آنها آزمایش انجام دهیم. در ابتدای تابع، ویژگیهای مورد نظر یا به عبارتی ستونهای دیتافریم را تعریف میکنیم:
def CreateDataset(nD:int,
MinN:int,
MaxN:int,
MinK:int,
MaxK:int) -> pd.DataFrame:
Columns = ['Min', 'Max', 'Range',
'M', 'S', 'CV', 'M + S', 'M + 2S',
'Q1', 'Q2', 'Q3', 'IQR',
'K', 'N']این ستونها به شکل زیر یک معیار آماری را نشان میدهند:
| توضیح | اسم ستون |
| کمترین (Minimum) شماره سریال یافتشده | Min |
| بیشترین (Maximum) شماره سریال یافتشده | Max |
| دامنه (Range) بین بیشترین و کمترین شماره سریال یافتشده | Range |
| میانگین (Mean) شماره سریالهای یافتشده | M |
| انحراف معیار (Standard Deviation) شماره سریالهای یافتشده | S |
| ضریب تغییرات (Coefficient of Variation) شماره سریالهای یافتشده | CV |
| میانگین به علاوه انحراف معیار | M + S |
| میانگین به علاوه دو برابر انحراف معیار | M + 2S |
| چارک اول (First Quartile) شماره سریالهای یافت شده | Q1 |
| چارک دوم (Second Quartile) یا میانه (Median) شماره سریالهای یافت شده | Q2 |
| چارک سوم (Third Quartile) شماره سریالهای یافت شده | Q3 |
| دامنه میان چارکی (Interquartile Range) شماره سریالهای یافت شده | IQR |
| تعداد تانکهای یافت شده | K |
| تعداد واقعی تانکها | N |
به این ترتیب تعداد زیادی معیار آماری تعریف میکنیم که هر مورد را محاسبه خواهیم کرد. این معیارها برای درک بهتر مجموعه داده و انجام پیشبینیهای بهتر میتواند مفید باشد. توجه داشته باشید که ممکن است ارتباطات پیچیدهتری بین ویژگی هدف (Target Feature) و ویژگیهای ورودی وجود داشته باشد، بنابراین سعی میکنیم تا بخش زیادی از این روابط را محاسبه و ذخیره کنیم، به این ترتیب مدل نهایی امکانات بیشتری برای پیشبینی خواهد داشت.
علاوه بر موارد آورده شده، میتوان نسبت این معیارها، لگاریتم آنها، حاصلضرب و …. را نیز آورد. این فرآیند مشابه روند استخراج ویژگی (Feature Extraction) در علم داده (Data Science) است. به عنوان داده اولیه و Index
مربوط به دیتافریم نیز از کدهای زیر استفاده میکنیم و دیتافریم را میسازیم:
def CreateDataset(nD:int,
MinN:int,
MaxN:int,
MinK:int,
MaxK:int) -> pd.DataFrame:
Columns = ['Min', 'Max', 'Range',
'M', 'S', 'CV', 'M + S', 'M + 2S',
'Q1', 'Q2', 'Q3', 'IQR',
'K', 'N']
Data = np.zeros(shape=(nD, len(Columns)),
dtype=np.float32)
Index = np.arange(start=0, stop=nD, step=1)
DF = pd.DataFrame(data=Data, columns=Columns, index=Index)توجه داشته باشید که در نتیجه این کد، دیتافریم حاصل دارای ۱۴ ستون و nD
سطر خواهد بود که تمامی مقادیر برابر با ۰ خواهد بود. حال یک حلقه ایجاد میکنیم که به تعداد nD
بار تکرار شده و در هر بار اجرا یک سطر از دیتافریم ایجاد شده را تکمیل کند:
def CreateDataset(nD:int,
MinN:int,
MaxN:int,
MinK:int,
MaxK:int) -> pd.DataFrame:
Columns = ['Min', 'Max', 'Range',
'M', 'S', 'CV', 'M + S', 'M + 2S',
'Q1', 'Q2', 'Q3', 'IQR',
'K', 'N']
Data = np.zeros(shape=(nD, len(Columns)),
dtype=np.float32)
Index = np.arange(start=0, stop=nD, step=1)
DF = pd.DataFrame(data=Data, columns=Columns, index=Index)
for i in range(nD):حال داخل حلقه باید مقدار N
را تعیین کنیم و سپس مقدار K
را انتخاب کنیم:
def CreateDataset(nD:int,
MinN:int,
MaxN:int,
MinK:int,
MaxK:int) -> pd.DataFrame:
Columns = ['Min', 'Max', 'Range',
'M', 'S', 'CV', 'M + S', 'M + 2S',
'Q1', 'Q2', 'Q3', 'IQR',
'K', 'N']
Data = np.zeros(shape=(nD, len(Columns)),
dtype=np.float32)
Index = np.arange(start=0, stop=nD, step=1)
DF = pd.DataFrame(data=Data, columns=Columns, index=Index)
for i in range(nD):
N = np.random.randint(low=MinN, high=MaxN + 1)
K = np.random.randint(low=MinK, high=min(MaxK + 1, N + 1))توجه داشته باشید که اندازه جمعیت اولیه N
است، بنابراین مقدار K
نمیتواند بیشتر از N
باشد، به همین دلیل مقدار high
برای انتخاب K
برابر با MaxK
نبوده و برابر با min(MaxK + 1, N + 1)
است.
حال میدانیم که چه تعداد تانک توسط آلمانیها تولید شده است و چه تعداد تانک باید توسط متفقین یافته شود. برای نمونهبرداری تصادفی از تانکها، ابتدا شماره سریال تمامی تانکها را با تابع numpy.arange
ایجاد میکنیم و در متغیر All
ذخیره میکنیم، سپس به تعداد K
مورد تانک از بین آنها انتخاب میکنیم:
def CreateDataset(nD:int,
MinN:int,
MaxN:int,
MinK:int,
MaxK:int) -> pd.DataFrame:
Columns = ['Min', 'Max', 'Range',
'M', 'S', 'CV', 'M + S', 'M + 2S',
'Q1', 'Q2', 'Q3', 'IQR',
'K', 'N']
Data = np.zeros(shape=(nD, len(Columns)),
dtype=np.float32)
Index = np.arange(start=0, stop=nD, step=1)
DF = pd.DataFrame(data=Data, columns=Columns, index=Index)
for i in range(nD):
N = np.random.randint(low=MinN, high=MaxN + 1)
K = np.random.randint(low=MinK, high=min(MaxK + 1, N + 1))
All = np.arange(start=1, stop=N + 1, step=1)
X = np.random.choice(a=All, size=K, replace=False)توجه داشته باشید که ورودی replace
مربوط به تابع numpy.random.choice
تعیین میکند که آیا یک مورد میتواند چندین بار انتخاب شود که باید خاموش شود و به همین دلیل مقدار False
به خود گرفته است. حال معیارهای گفته شده را یک به یک محاسبه میکنیم تا به دیتافریم اضافه کنیم:
def CreateDataset(nD:int,
MinN:int,
MaxN:int,
MinK:int,
MaxK:int) -> pd.DataFrame:
Columns = ['Min', 'Max', 'Range',
'M', 'S', 'CV', 'M + S', 'M + 2S',
'Q1', 'Q2', 'Q3', 'IQR',
'K', 'N']
Data = np.zeros(shape=(nD, len(Columns)),
dtype=np.float32)
Index = np.arange(start=0, stop=nD, step=1)
DF = pd.DataFrame(data=Data, columns=Columns, index=Index)
for i in range(nD):
N = np.random.randint(low=MinN, high=MaxN + 1)
K = np.random.randint(low=MinK, high=min(MaxK + 1, N + 1))
All = np.arange(start=1, stop=N + 1, step=1)
X = np.random.choice(a=All, size=K, replace=False)
Min = X.min()
Max = X.max()
Range = Max - Min
M = X.mean()
S = X.std()
CV = S / M
MS = M + S
M2S = M + 2 * S
Q1 = np.quantile(X, q=0.25)
Q2 = np.quantile(X, q=0.5)
Q3 = np.quantile(X, q=0.75)
IQR = Q3 - Q1حال میتوانیم مقادیر محاسبه شده را به سطر i
دیتافریم اضافه کنیم و در نهایت دیتافریم حاصل را در خروجی تابع برگردانیم:
def CreateDataset(nD:int,
MinN:int,
MaxN:int,
MinK:int,
MaxK:int) -> pd.DataFrame:
Columns = ['Min', 'Max', 'Range',
'M', 'S', 'CV', 'M + S', 'M + 2S',
'Q1', 'Q2', 'Q3', 'IQR',
'K', 'N']
Data = np.zeros(shape=(nD, len(Columns)),
dtype=np.float32)
Index = np.arange(start=0, stop=nD, step=1)
DF = pd.DataFrame(data=Data, columns=Columns, index=Index)
for i in range(nD):
N = np.random.randint(low=MinN, high=MaxN + 1)
K = np.random.randint(low=MinK, high=min(MaxK + 1, N + 1))
All = np.arange(start=1, stop=N + 1, step=1)
X = np.random.choice(a=All, size=K, replace=False)
Min = X.min()
Max = X.max()
Range = Max - Min
M = X.mean()
S = X.std()
CV = S / M
MS = M + S
M2S = M + 2 * S
Q1 = np.quantile(X, q=0.25)
Q2 = np.quantile(X, q=0.5)
Q3 = np.quantile(X, q=0.75)
IQR = Q3 - Q1
DF.iloc[i] = [Min, Max, Range, M, S, CV, MS, M2S, Q1, Q2, Q3, IQR, K, N]
return DFبه این ترتیب تابع مربوط به تولید مجموعه داده آماده است. به شکل زیر میتوانیم یک مجموعه داده تولید کنیم:
DF = CreateDataset(2000, 100, 300, 50, 150)به این ترتیب ۲۰۰۰ سناریوی تصادفی ایجاد خواهد شد که در هر کدام آلمانیها بین ۱۰۰ تا ۳۰۰ تانک خواهند ساخت و متفقین بیت ۵۰ تا ۱۵۰ مورد از آنها را خواهند یافت. توجه داشته باشید که حد بالای مقدار K
به عدد N
محدود شده است.
مصورسازی همبستگی بین ستونهای مجموعه داده برای مسئله تانک آلمانی
اولین موردی که میتوانیم در مورد مجموعه داده بررسی کنیم، بررسی همبستگی (Correlation) بین ستونها است.
با توجه به اینکه ممکن است روابط غیرخطی بین ستونها وجود داشته باشد، از ضریب همبستگی اسپیرمن (Spearman Correlation Coefficient) استفاده خواهیم کرد. به این منظور تابع با اسم PlotCorrelation
ایجاد میکنیم. این تابع در ورودی دیتافریم مجموعه داده را دریافت خواهد کرد و تنها یک نمودار نشان خواهد داد:
def PlotCorrelation(DF:pd.DataFrame) -> None:
C = DF.corr(method='spearman')
sb.heatmap(C, cmap='RdYlGn',
annot=True, fmt='.2f',
xticklabels=DF.columns,
yticklabels=DF.columns)
plt.title('Spearman Correlation Coeficient Between Dataset Columns')
plt.show()این نمودار که Heat Map نام دارد، به کمک کتابخانه Seaborn
رسم میشود. برای استفاده از این تابع، به شکل زیر عمل میکنیم:
PlotCorrelation(DF)در خروجی این کد، نمودار زیر حاصل میشود:
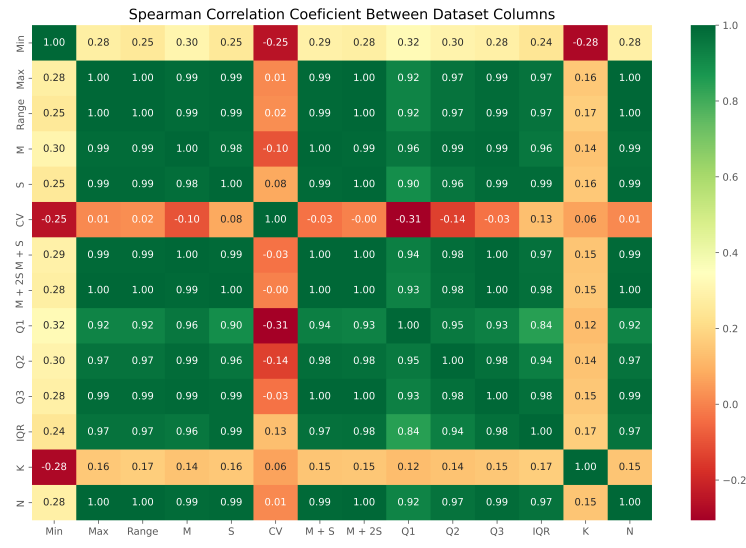
میتوانیم مشاهده کنیم که بین اعداد اغلب همبستگی شدیدی وجود دارد، به جز Min
، CV
و K
که به دلایلی قابل توجیه است. با توجه به اینکه قصد داریم ستون N
را پیشبینی کنیم، هر ستون دیگری که با آن همبستگی قدرتمندی داشته باشد، میتواند در انجام پیشبینی به ما کمک کند. به این جهت، تمامی ستونها به جز N
، K
، Q1
و Min
دارای همبستگی بالای ۰/۹۷ هستند که مقدار قابل توجهی است.
رسم نمودارهای نقطهای برای مسئله تانک آلمانی
نمودار دیگری که میتواند بین ویژگی هدف و سایر ویژگیهای ورودی رسم شود، نمودار نقطهای (Scatter Plot) است که برای نشان دادن ارتباط بین دو متغیر بسیار مفید است. به این منظور تابع زیر را استفاده خواهیم کرد:
def ScatterPlot(DF:pd.DataFrame) -> None:
yColumn = 'N'
for xColumn in DF.columns:
if xColumn != yColumn:
plt.scatter(DF.loc[:, xColumn],
DF.loc[:, yColumn],
s=20, c='crimson',
alpha=0.8, marker='o')
plt.xlabel(xColumn)
plt.ylabel(yColumn)
plt.show()توجه داشته باشید که ستون N
همواره ستون هدف است و تمامی ستونهای غیر از N
ستون ویژگی ورودی هستند، بنابراین yColumn
برابر با N
تعریف میشود و xColumn
با کمک یک حلقه مدام تغییر میکند و عبارت xColumn != yColumn
از برابر نبودن دو متغیر اطمینان ایجاد میکند. این تابع به شکل زیر استفاده میشود:
ScatterPlot(DF)در خروجی این سطر از کد، ۱۳ نمودار حاصل میشود که در GIF زیر پشت سر هم آمدهاند:
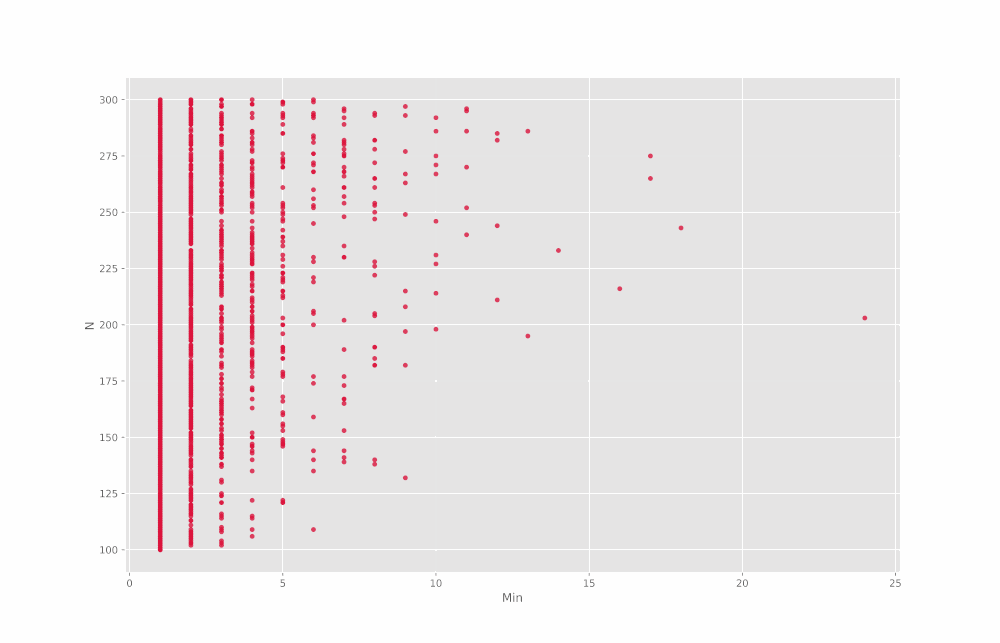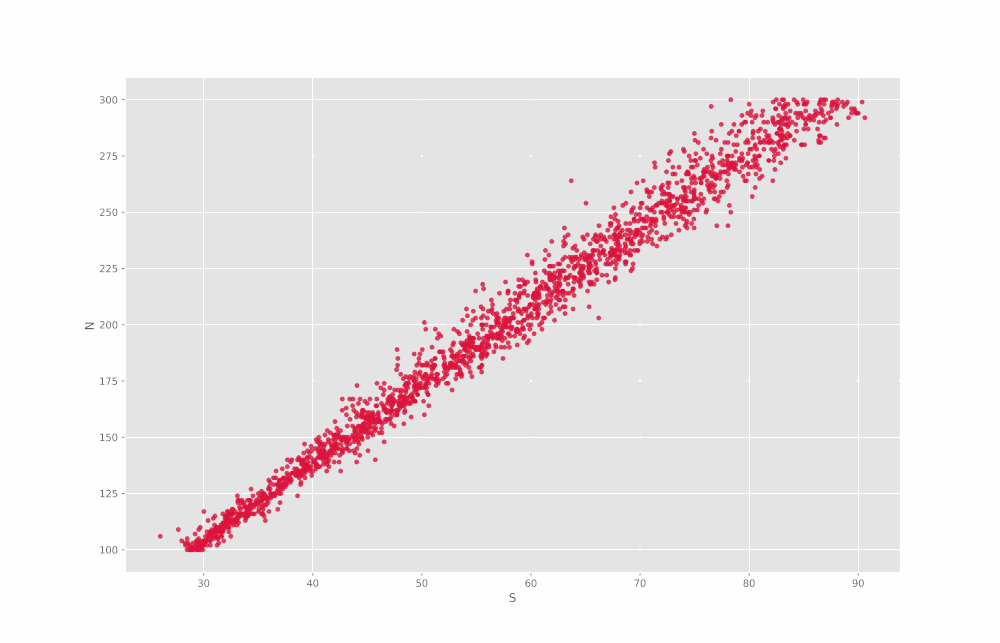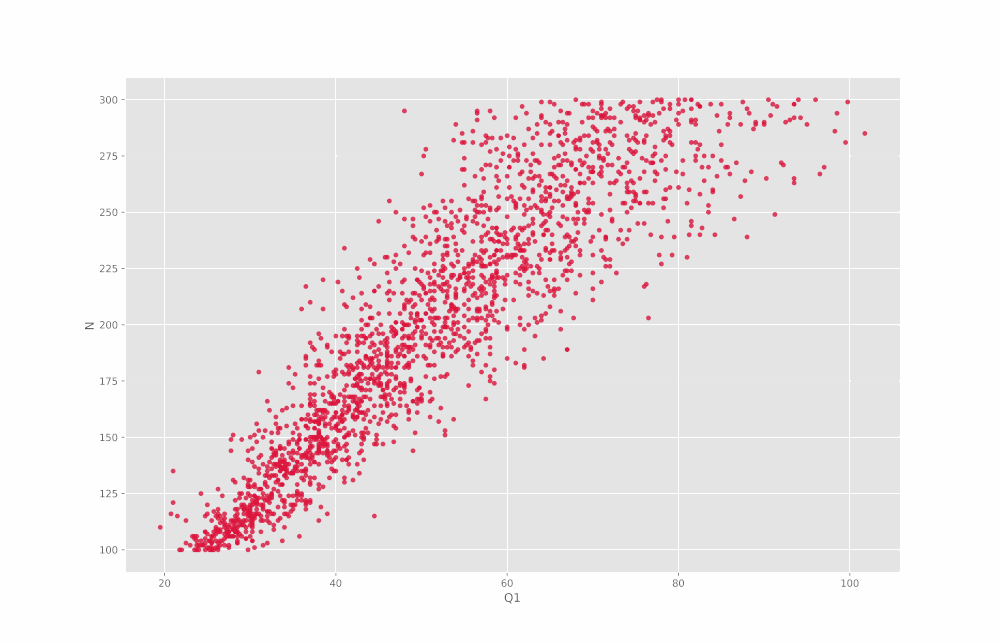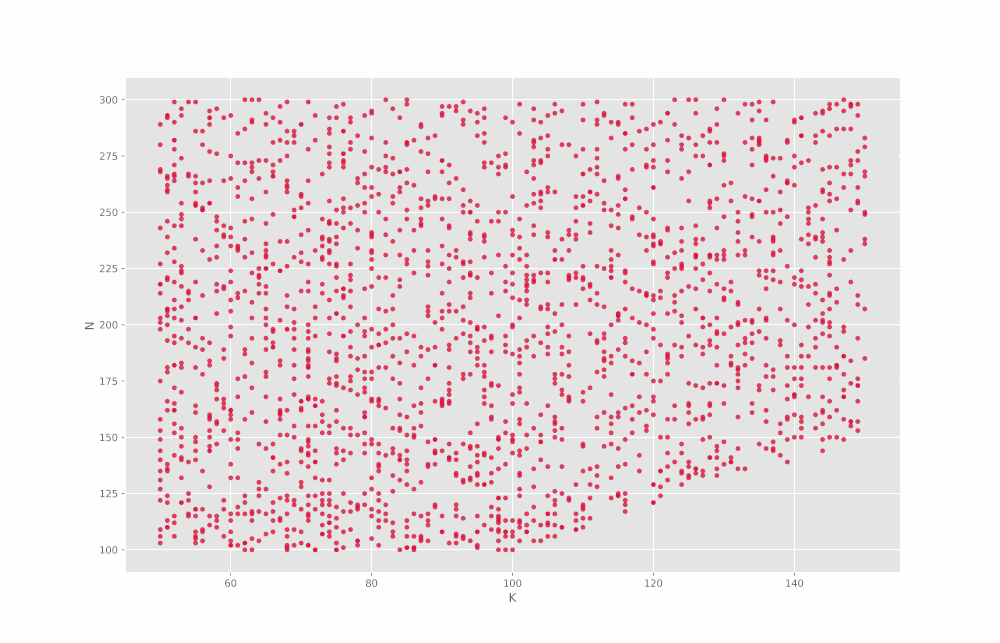
به این ترتیب مشاهده میکنیم که در اغلب موارد یک ارتباط تقریباً خطی بین مقادیر قابل مشاهده است. اما توجه داشته باشید که برای Min
نمودار زیر را داریم:
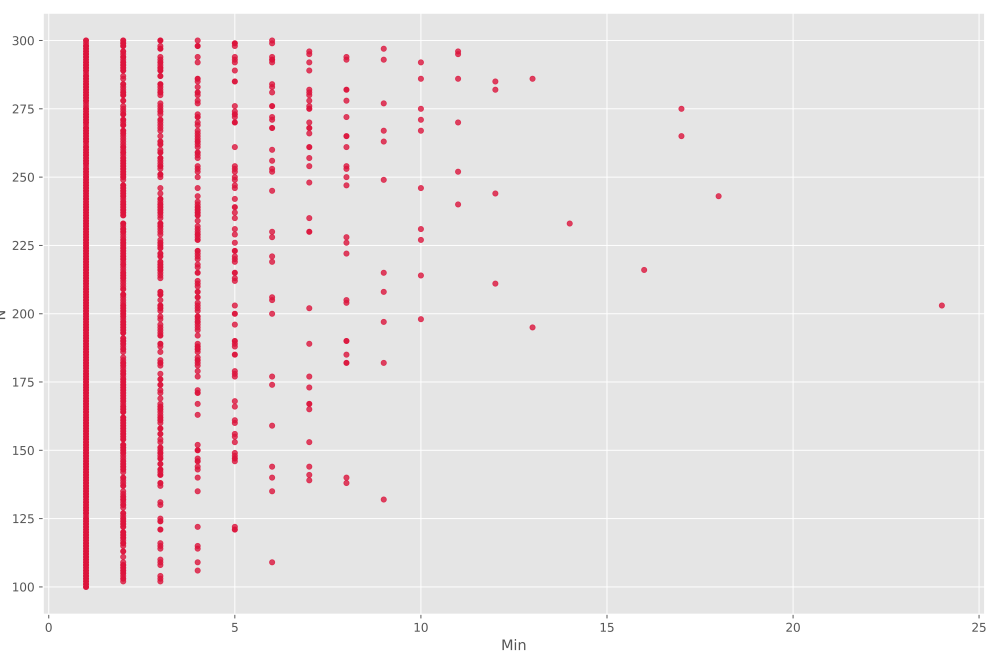
مشاهده میکنیم که در این نمودار همبستگی چندان خوبی مشاهده نمیشود، که با توجه به ماهیت مسئله و حد پایین بودن Min
طبیعی نیز است. اما همچنان با افزایش Min
شاهد یک روند افزایشی در N
میباشیم. برای CV
نیز نمودار زیر حاصل میشود:
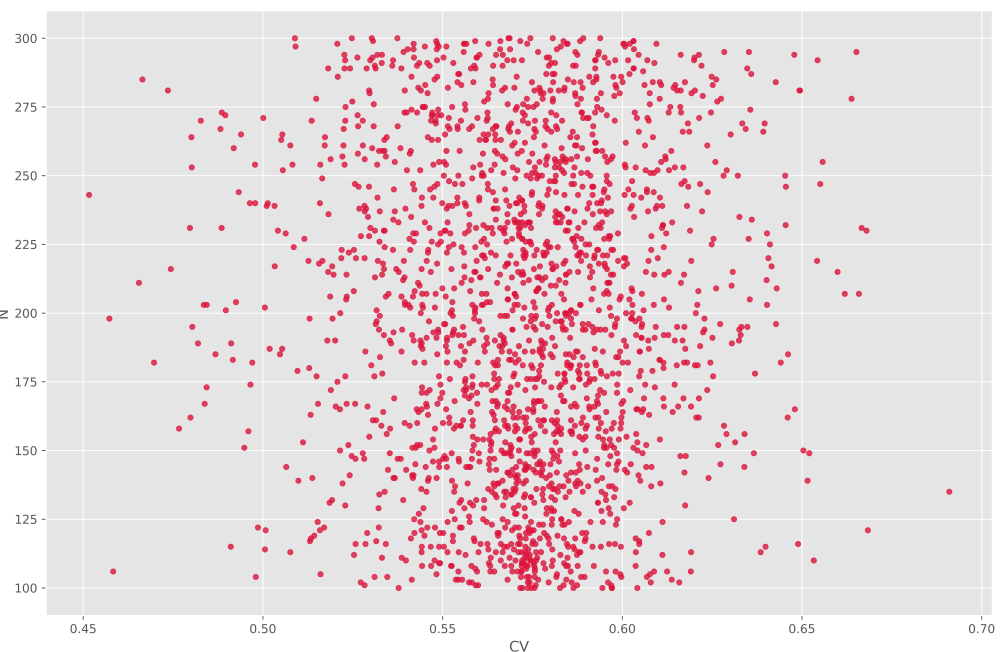
در این نمودار هیچگونه همبستگی مشاهده نمیشود، اما میتوان گفت مقادیر CV
حول خط $$ x = 0.57 $$ پراکنده شدهاند و با دور شدن از این خط چگالی (Density) دادهها نیز کاهش پیدا میکند. برای K
نیز نمودار زیر حاصل میشود:
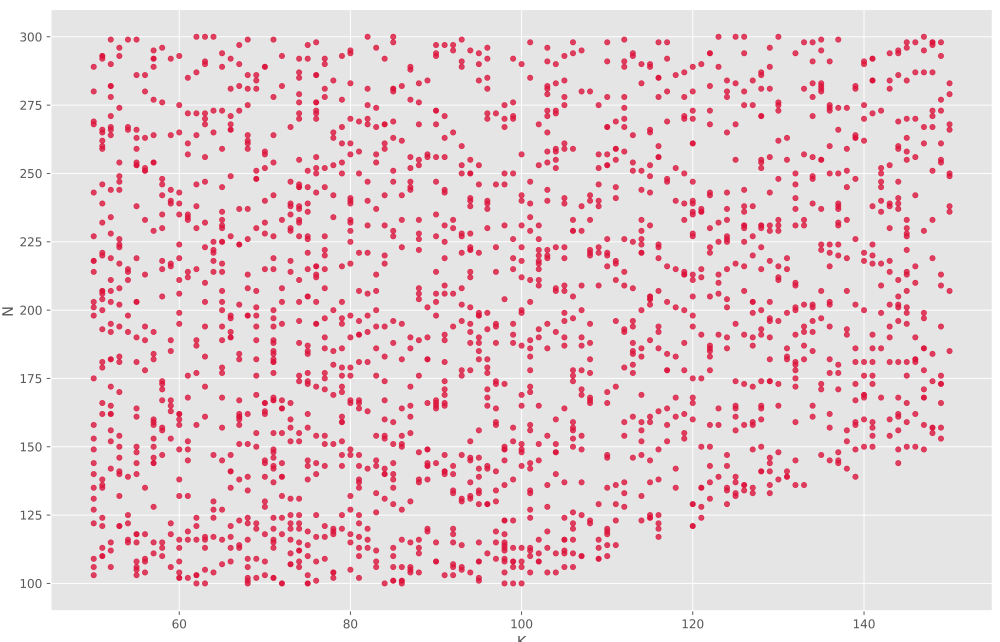
مشاهده میکنیم که برای بازه $$ x leq 100 $$ مقادیر N
به صورت یکنواخت پخش شدهاند، درحالیکه که برای بازه $$ x gt 100 $$ این شرایط حاکم نیست و حد پایین N
رفتهرفته افزایش مییابد. با توجه به اینکه اندازه جمعیت اولیه N
است و در بیشترین حالت میتوانیم N
نمونه از جمعیت اولیه انتخاب کنیم، وجود این خط قابل توجیه است. در مورد سایر موارد نیز میتوانید تکتک نمودارها بررسی کنید و متوجه روابط بین هر ویژگی با ویژگی هدف شوید.
پیادهسازی فرمول یافته شده توسط کارشناسان آمار و ارزیابی آن برای مسئله تانک آلمانی
به این منظور ابتدا از دیتافریم ایجاد شده، ستون هدف ( N
) و مقادیر Max
و K
را به شکل آرایه (Array) استخراج میکنیم:
Y = DF.loc[:, 'N'].to_numpy()
M = DF.loc[:, 'Max'].to_numpy()
K = DF.loc[:, 'K'].to_numpy()حال میتوانیم خروجی فرمول به دست آمده را نیز محاسبه کنیم:
Ps = M + M / K - 1طراحی تابع گزارش رگرسیون برای مسئله تانک آلمانی
حال مقادیر پیشبینی شده توسط رابطه یافته شده را داریم. حال باید تابعی طراحی کنیم تا معیارهای ارزیابی رگرسیون را محاسبه و در خروجی نمایش دهد.
تابعی به اسم RegressionReport
تعریف میکنیم که در ورودی مقادیر واقعی (Target Values, Observed Values) و مقادیر پیشبینی شده (Predicted Values) را به همراه نام مجموعه داده دریافت میکند:
def RegressionReport(Y:np.ndarray, P:np.ndarray, Dataset:str) -> None:حال با استفاده از توابع موجود در sklearn.metrics
معیارهایی همچون میانگین مربعات خطا (Mean Squared Error یا MSE)، میانگین قدر مطلق خطا (Mean Absolute Error یا MAE)، میانگین قدر مطلق درصد خطا (Mean Absolute Percentage Error یا MAPE) و ضریب تعیین (Coefficient of Determination یا R2 Score) قابل محاسبه است. ۳ معیار دیگر نیز براساس MSE
و MAE
قابل محاسبه هستند:
def RegressionReport(Y:np.ndarray, P:np.ndarray, Dataset:str) -> None:
MSE = met.mean_squared_error(Y, P)
RMSE = MSE ** 0.5
Range = Y.max() - Y.min()
NRMSE = 100 * RMSE / Range
MAE = met.mean_absolute_error(Y, P)
NMAE = 100 * MAE / Range
MAPE = 100 * met.mean_absolute_percentage_error(Y, P)
R2 = 100 * met.r2_score(Y, P)حال باید معیارهای محاسبه شده را به شکل یک متن نمایش دهیم:
def RegressionReport(Y:np.ndarray, P:np.ndarray, Dataset:str) -> None:
MSE = met.mean_squared_error(Y, P)
RMSE = MSE ** 0.5
Range = Y.max() - Y.min()
NRMSE = 100 * RMSE / Range
MAE = met.mean_absolute_error(Y, P)
NMAE = 100 * MAE / Range
MAPE = 100 * met.mean_absolute_percentage_error(Y, P)
R2 = 100 * met.r2_score(Y, P)
print(f'Regression Report For {Dataset}:')
print(f'MSE: {MSE:.2f}')
print(f'RMSE: {RMSE:.2f}')
print(f'NRMSE: {NRMSE:.2f} %')
print(f'MAE: {MAE:.2f}')
print(f'NMAE: {NMAE:.2f} %')
print(f'MAPE: {MAPE:.2f} %')
print(f'R2: {R2:.2f} %')به این ترتیب این تابع کامل میشود و میتوانیم آن را به شکل زیر استفاده کنیم:
RegressionReport(Y, Ps, 'Statistic Formula')در این شرایط یک گزارش از کیفیت پیشبینی انجام شده به شکل زیر در خروجی نوشته خواهد شد:
Regression Report For Statistic Formula:
MSE: 3.76
RMSE: 1.94
NRMSE: 0.97 %
MAE: 1.22
NMAE: 0.61 %
MAPE: 0.59 %
R2: 99.88 %به این ترتیب مشاهده میکنیم که ضریب تعیین به عدد ۹۹/۸۸% رسیده است که عدد بسیار مناسبی است. معیار MAPE
نیز عدد ۰/۵۹% را نشان میدهد که خطایی کمتر از ۱% بوده و بسیار مناسب است.
طراحی تابع رسم نمودار رگرسیون برای مسئله تانک آلمانی
اگر قصد داشته باشیم که برای رگرسیون انجام شده یک نمودار نیز رسم کنیم، میتوانیم یک تابع به شکل زیر ایجاد کنیم:
def RegressionPlot(Y:np.ndarray, P:np.ndarray, Dataset:str) -> None:
a = min(Y.min(), P.min())
b = max(Y.max(), P.max())
ab = np.array([a, b])
plt.scatter(Y, P, s=20, c='teal', marker='o', label='Data')
plt.plot(ab, ab, ls='-', lw=1, c='k', label='Y = X')
plt.plot(ab, 0.9 * ab, ls='--', lw=0.9, c='r', label='Y = 0.8 * X')
plt.plot(ab, 1.1 * ab, ls='--', lw=0.9, c='r', label='Y = 1.1 * X')
plt.title(f'Regression Plot For {Dataset}')
plt.xlabel('Target Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.show()این تابع نیز مشابه قبل در ورودی مقادیر واقعی، مقادیر پیشبینی شده و نام مجموعه داده را دریافت میکنم. بر روی نمودار حاصل با استفاده از تابع matplotlib.pyplot.scatter
هر داده به شکل یک نقطه نمایش داده خواهد شد. ۳ خط راهنما نیز رسم خواهند شد تا بازه مربوط به خطای $$ [ -10%,; +10%] $$ را نمایش دهد. از این تابع به شکل زیر استفاده میکنیم:
RegressionPlot(Y, Ps, 'Statistic Formula')و در خروجی نمودار زیر حاصل میشود:
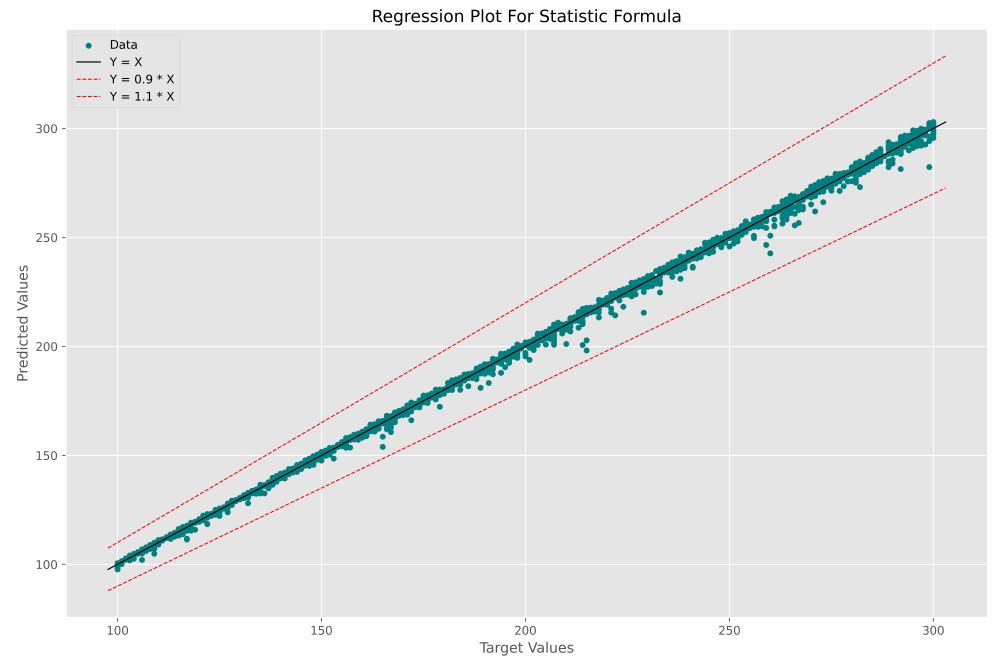
به این ترتیب مشاهده میکنیم که اکثر دادهها در فاصله بسیار نزدیکی از خط $$ y = x $$ قرار گرفتهاند که مطلوب است. در کل مجموعه داده نیز هیچ دادهای خارج از دو خط قرمز وجود ندارد، بنابراین بیشترین قدر مطلق درصد خطا کمتر از ۱۰% است. به این ترتیب به عنوان یک نتیجهگیری میتوان گفت که فرمول پیشنهاد شده توسط کارشناسان آمار از دقت بسیار بالایی برخوردار است.
انجام پیشبینی با استفاده از مدلهای یادگیری ماشین برای مسئله تانک آلمانی
دیدیم که فرمول محاسبه شده براساس روابط آورده شده، منجر به دقت خوبی در پیشبینی میشود، اما آیا تنها راه ممکن برای حل این مسئله استفاده از روابط بسته ریاضی است؟ مسلماً خیر. با توجه به امکانات محاسباتی که وجود دارد و پیشرفتی که در حوزه علم داده و یادگیری ماشین رخ داده است، میتوانیم از مدلهای یادگیری ماشین نیز استفاده کنیم.
به منظور آموزش یک مدل رگرسیون، به ویژگیهای ورودی مجموعه داده (X) و ویژگیهای هدف مجموعه داده (Y) نیاز داریم. در این مسئله ستون N
دیتافریم ویژگی هدف و سایر ستونها ویژگیهای ورودی هستند. بنابراین به شکل زیر میتوانیم این ویژگیها را جدا کنیم:
X0 = DF.drop(labels=['N'], axis=1, inplace=False).to_numpy()
Y0 = DF.loc[:, ['N']].to_numpy()اصلاح مقیاس مجموعه داده برای مسئله تانک آلمانی
با توجه به اینکه این ویژگیها دارای مقیاس (Scale) و بازه (Range) متفاوتی هستند، باید آنها را اصلاح مقیاس (Rescaling) کنیم. بنابراین ویژگیهای قبل از اصلاح مقیاس را X0
و Y0
نامگذاری میکنیم. در مرحله بعد باید ویژگیها اصلاح مقیاس شوند، به همین دلیل باید ابتدا به دو مجموعه داده آموزش (Train Dataset) و مجموعه داده آزمایش (Test Dataset) تقسیم شود. به شکل زیر ابتدا تعداد دادهها محاسبه سپس 80% دادهها برای Train انتخاب میشود:
nD = X0.shape[0]
nDtr = round(0.8 * nD)
trX0 = X0[:nDtr]
teX0 = X0[nDtr:]
trY0 = Y0[:nDtr]
teY0 = Y0[nDtr:]توجه داشته باشید که چون مجموعه داده با کمک اعداد تصادفی تولید شده است، هیچ ترتیب معناداری بین دادهها وجود ندارد، بنابراین به هم ریختن تصادفی ترتیب آن یا Shuffle کردن تفاوتی ایجاد نخواهد کرد، به همین دلیل از تابع زیر استفاده نمیکنیم.
sklearn.model_selection.train_test_split
حال با استفاده از sklearn.preprocessing.StandardScaler
ویژگیها را اصلاح مقیاس میکنیم.
توجه داشته باشید که چون یک مسئله رگرسیون داریم، باید ویژگی هدف نیز به این شکل اصلاح مقیاس شود:
xScaler = pp.StandardScaler()
trX = xScaler.fit_transform(trX0)
teX = xScaler.transform(teX0)
yScaler = pp.StandardScaler()
trY = yScaler.fit_transform(trY0)
teY = yScaler.transform(teY0)ایجاد و آموزش مدل مسئله تانک آلمانی
قبل از ایجاد مدل، باید ابتدا در مورد نوع آن تصمیم بگیریم. با توجه به اینکه یک مسئله و یک مجموعه داده کوچک داریم، همچنین میدانیم که بین اکثر ویژگیهای ورودی با ویژگی هدف یک ارتباط خطی وجود دارد، از مدل رگرسیون خطی (Linear Regression) استفاده میکنیم و آن را بر روی مجموعه داده آموزش، آموزش میدهیم:
Model = lm.LinearRegression()
Model.fit(trX, trY)توجه داشته باشید که در اغلب شرایط سعی میکنیم از سادهترین مدل ممکن برای شروع استفاده کنیم.
انجام پیشبینی مسئله تانک آلمانی
برای انجام پیشبینی به شکل زیر عمل میکنیم:
teP = Model.predict(teX)توجه داشته باشید که این مقادیر پیشبینی شده در مقیاس اصلی ویژگی هدف نیست و برای اینکه آن را به مقیاس اصلی برگردانیم، باید به شکل زیر عمل کنیم:
teP0 = yScaler.inverse_transform(teP)با توجه به اینکه قصد داریم معیارهای مختلفی برای ارزیابی پیشبینیهای مدل استفاده کنیم، باید پیشبینیهای انجام شده و مقادیر هدف در مقیاس اولیه باشند. حال میتوانیم از تابع RegressionReport
برای تهیه یک گزارش از عملکرد مدل استفاده کنیم:
RegressionReport(teY0, teP0, 'Linear Regression Model (Test Dataset)')که خواهیم داشت:
Regression Report For Linear Regression Model (Test Dataset):
MSE: 2.50
RMSE: 1.58
NRMSE: 0.79 %
MAE: 1.10
NMAE: 0.55 %
MAPE: 0.55 %
R2: 99.93 %به این ترتیب مشاهده میکنیم که مدل ایجاد شده نیز به ضریب تعیین ۹۹/۹۳% دست یافته است که عدد بسیار خوبی است. این مدل به دلیل در دسترس بودن ویژگیهای بیشتر و همچنین بهینهسازی وزنهای خود، توانسته ضریب تعیین را به اندازه ۰/۰۵% بهبود دهد. برای رسم نمودار رگرسیون مدل رگرسیون خطی نیز مشابه قبل کد زیر را استفاده میکنیم:
RegressionPlot(teY0, teP0, 'Linear Regression Model (Test Dataset)')پس از اجرای این کد نیز نمودار زیر حاصل میشود:
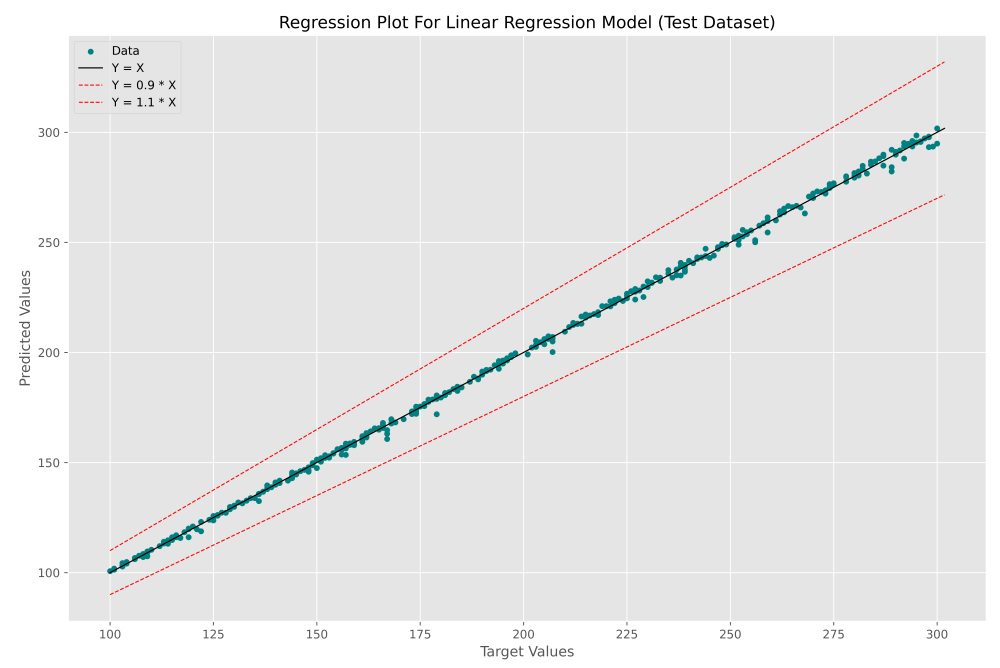
به این ترتیب همانطور که انتظار داشتیم، یک نمودار بسیار مناسب حاصل میشود که در نقاط پراکندگی بسیار کمی حوله خط $$ y = x $$ دارند. به این ترتیب متوجه میشویم که برای حل اینگونه مسائل الزاماً نیاز نیست روابط پیچیده ریاضی را حل کنیم و مدلهای یادگیری ماشین به جای ما میتوانند معادل این کار را انجام دهد.
مدل رگرسیون خطی چگونه پیشبینی انجام داده است؟
به این منظور باید رابطه برازش شده توسط مدل را به دست آوریم. یک مدل رگرسیون خطی به شکل زیر ویژگی هدف را پیشبینی میکند:
$$
hat{y}=b+w_1 times x_1+w_2 times x_2+cdots+w_n times x_n=b+sum_{i=1}^n w_i times x_i=W^T x+b
$$
در رابطه فوق تنها مقادیر b و w توسط الگوریتمهای بهینهساز (Optimizer) محاسبه میشوند. این موارد در داخل Model
ایجاد شده وجود دارد. اما توجه داشته باشید که قبل از وارد شدن ویژگیها به مدل، آنها را اصلاح مقیاس کردیم، به همین دلیل روابط حاصل پیچیده خواهد بود، به همین جهت میتوانیم تمامی فرآیند Scaling و Inverse Scaling را حذف کنیم تا ضرایب (Coefficient) و بایاس (Bias) در مقیاس اصلی به دست آید. انجام این فرآیند برای تمامی مدلها امکانپذیر نیست:
nD = X0.shape[0]
nDtr = round(0.8 * nD)
trX0 = X0[:nDtr]
teX0 = X0[nDtr:]
trY0 = Y0[:nDtr]
teY0 = Y0[nDtr:]
Model = lm.LinearRegression()
Model.fit(trX0, trY0)حال میتوانیم با استفاده از دو Attribute زیر مقادیر ضرایب و بایاس را استخراج کنید:
W = Model.coef_
B = Model.intercept_جنس این دو متغیر را میتوانیم به شکل زیر بررسی کنیم:
print(type(W))
print(type(B))که خواهیم داشت:
به این ترتیب مشاهده میکنیم که هر دو متغیر آرایه هستند. حال میتوانیم ابعاد آنها را بررسی کنیم:
print(W.shape)
print(B.shape)که خواهیم داشت:
(1, 13)
(1,)به این ترتیب مشاهده میکنیم آرایه وزن ابعاد $$ 1 times 13 $$ دارد که عدد ۱۳ نشاندهنده تعداد ویژگیهای ورودی و عدد ۱ نشاندهنده تعداد ویژگیهای هدف است. آرایه بایاس نیز باید یک عدد Float میبود که به دلیل وجود یک ویژگی هدف به یک آرایه با ابعاد ۱ در آمده است. به شکل زیر تعریف W
و B
را اصلاح میکنیم:
W = Model.coef_[0]
B = Model.intercept_[0]حال باید اسم ویژگیهای ورودی را نیز به ترتیبی که وجود دارد استخراج کنیم. به این منظور از کد زیر استفاده میکنیم:
FeatureNames = [FeatureName for FeatureName in DF.columns if FeatureName != 'N']این کد اسم تمامی ستونهای دیتافریم ساخته شده به جز ستون N
را به ترتیب استخراج میکند. حال کد زیر را نوشته و اجرا میکنیم:
print('N = ', end='')
for w, FeatureName in zip(W, FeatureNames):
if '+' in FeatureName:
FeatureName = f'({FeatureName})'
if w > 0:
print(f' + {w:.2f} * {FeatureName}', end='')
else:
print(f' - {abs(w):.2f} * {FeatureName}', end='')
if B > 0:
print(f' + {B:.2f}', end='n')
else:
print(f' - {B:.2f}', end='n')این کد به گونهای طراحی شده است که فرمول یافته شده توسط مدل رگرسیون خطی را برای ما تشکیل میدهد و خروجی زیر حاصل میشود:
N = 0.31 * Min + 0.73 * Max + 0.28 * Range - 1.14 * M + 0.33 * S - 14.07 * CV + 2.08 * (M + S) - 1.11 * (M + 2S) + 0.02 * Q1 + 0.02 * Q2 + 0.04 * Q3 - 0.03 * IQR - 0.02 * K + 9.31به این ترتیب مشاهده میکنیم که یک رابطه ریاضی بسته حاصل میشود همانند رابطهای که کارشناسان آمار محاسبه کرده بودند. توجه داشته باشید که ویژگی Range
ترکیب خطی دو ویژگی Min
و Max
است. ویژگی IQR
نیز ترکیب خطی دو ویژگی Q1
و Q3
است. این گزاره در مورد دو ویژگی M + S
و M + 2S
نیز صحیح است. از طرفی میدانیم که مدل رگرسیون خطی یک ترکیب خطی از ویژگیهای ورودی ایجاد میکند، بنابراین این موارد میتوانند حذف شوند و تنها ویژگیهای زیر باقی بمانند:
Columns = ['Min', 'Max',
'M', 'S', 'CV',
'Q1', 'Q2', 'Q3',
'K', 'N']در این شرایط اگر دوباره کد مربوط به فرمول ریاضی حاصل از مدل را اجرا کنیم، به رابطه زیر خواهیم رسید:
N = 0.03 * Min + 1.01 * Max - 0.17 * M + 0.19 * S - 14.07 * CV + 0.04 * Q1 + 0.02 * Q2 + 0.01 * Q3 - 0.02 * K + 9.31در این حالت، وزنهای محاسبه شده به اعداد معقولی نزدیک میشود.
جمعبندی
به این ترتیب مشاهده میکنیم که برای حل این مسئله نگرش ریاضیاتی یک راه حل قوی و دقیقی ایجاد میکند که برای به دست آوردن آن نیاز به حل روابط پیچیده داریم و در مقابل یادگیری ماشین و علم داده به ما توصیه میکند ویژگیهای متفاوتی ایجاد کنیم و اجازه دهیم مدل یادگیری ماشین در مورد رابطه نهایی تصمیم بگیرد. در جهت ادامه این مطلب و تمرین میتوان به موارد زیر پرداخت:
- مشابه این مسئله در چه مواردی مشاهده میشود؟
- چرا امروزه شماره سریالها به شکل دنباله عددی ساده ساخته نمیشود؟
- چرا برای ارزیابی فرمول حاصل از روابط ریاضیاتی، مجموعه داده را به دو بخش Train و Test تقسیم نکردیم؟
- کد مربوط به استخراج فرمول را تحلیل کنید.
- اگر اصلاح مقیاس را با روش Min-Max Scaling انجام دهیم، رابطه زیر به دست میآید، این رابطه را چگونه میتوان تحلیل کرد؟
N = 0.00 * Min + 1.02 * Max - 0.10 * M + 0.06 * S - 0.02 * CV + 0.02 * Q1 + 0.01 * Q2 + 0.01 * Q3 - 0.01 * K + 0.00- چرا ضریب CV که قبلاً در حدود -14 بود به مقدار -0.02 رسید؟
- تنظیمات تابع CreateDataset را تغییر دهید و دقت حاصل از مدل را به این تنظیمات ارتباط دهید.
- اگر شماره سریالهای 3,21,28,36,49,56 یافته شده باشند، اندازه جمعیت اولیه را با استفاده از فرمول کارشناسان آمار پیشبینی کنید.
- برای مجموعه داده حاصل از کد زیر، نمودار همبستگی و نمودار نقطهای را رسم کنید:
DF = CreateDataset(2000, 100, 300, 5, 10)تفاوت ایجاد شده در نمودارها به چه دلیلی است؟ در این شرایط دقت مدلها و فرمول چه تغییر میکنید؟

