پیش بینی قیمت در پایتون — راهنمای گام به گام

حوزه بازارهای مالی، به دلیل اهمیت بالا و پیچیدگی‌های موجود، نیاز به تحلیل با استفاده از علم روز دارد که بخش قابل توجهی از آن، توسط هوش مصنوعی (Artificial Intelligence) و علم داده (Data Science) تأمین می‌شود. در این آموزش، به پیش بینی قیمت در پایتون می‌پردازیم.

برای تحلیل و پیش‌بینی قیمت، نیاز به داده‌هایی داریم که به طور کلی دو دسته هستند:

1. متغیرهای خرد (Micro) مانند قیمت یک نماد، حجم نماد و یا نمادهای دیگر
2. متغیرهای کلان (Macro) مانند قیمت جهانی طلا، قیمت جهانی نفت، شاخص‌ها

به طور کلی، برای انجام یک پیش‌بینی مطلوب، وجود تعداد زیادی متغیر خرد و تعدادی متغیر کلان مفید است. برای مثال، انجام یک پیش‌بینی مناسب برای سهمی در بورس ایران، می‌تواند به متغیرهای زیر نیاز داشته باشد:

1. متغیرهای مربوط به خود سهم
2. شاخص کل و شاخص هم‌وزن
3. نرخ سود بانکی
4. نرخ تورم
5. قیمت جهانی طلا
6. برخی شاخص‌های موجود در بازار فارکس (Foreign Exchange Market)

از طرفی، داده‌های کیفی مرتبط با «تحلیل فاندامنتال» (Fundamental Analysis) نیز می‌توانند اثر فراوانی داشته باشند که بهتر است به شکلی کمی‌سازی شده و وارد مجموعه داده شوند.

برخی داده‌ها از منابعی مانند «Google Trend» که نشان‌دهنده اقبال عمومی هستند نیز می‌توانند بسیار کمک‌کننده باشند. بنابراین، هرچه دامنه اطلاعات مورد استفاده وسیع‌تر باشد، تحلیل با اعتبار و دقت بیشتری صورت می‌گیرد. البته باید توجه داشت که داده‌ها باید از اعتبار بالایی برخوردار باشند، همچنین با توجه به نظم خاصی که در داده‌های سری زمانی وجود دارد، باید داده‌ها امکان ترکیب و «همجوشی» (Data Fusion) با یکدیگر را داشته باشند.

برای یادگیری برنامه‌نویسی با زبان پایتون، پیشنهاد می‌کنیم به مجموعه آموزش‌های مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.

فیلم آموزش پیش بینی نوسانات بازار سهام با هوش مصنوعی در پایتون Python در تم آف

کلیک کنید

پیش بینی قیمت در پایتون

حال برای پیاده‌سازی مدل‌ها و انجام پیش بینی قیمت در پایتون ، وارد محیط برنامه‌نویسی شده و کتابخانه‌های مورد نیاز را فراخوانی می‌کنیم:

import numpy as np
import pandas as pd
import datetime as dt
import yfinance as yf
import mplfinance as mplf
import sklearn.metrics as met
import matplotlib.pyplot as plt
import pandas_datareader as pdt
import sklearn.linear_model as lm
import sklearn.preprocessing as pp
import statsmodels.graphics.tsaplots as tsaplt

این کتابخانه‌ها به‌ترتیب برای موارد زیر استفاده خواهند شد:

فیلم آموزش کاربرد پایتون در بازارهای مالی – دریافت و پردازش قیمت رمزارزها (رایگان)

کلیک کنید

1. کار با آرایه‌ها و محاسبات برداری
2. کار با دیتافریم‌ها و داده‌ها
3. استفاده از تاریخ و زمان
4. دریافت داده
5. رسم نمودارهای مالی
6. محاسبه معیارهای ارزیابی مدل‌ها
7. رسم نمودار
8. دریافت داده
9. ایجاد و آموزش مدل‌های خطی
10. پیش‌پردازش داده
11. رسم نمودارهای تحلیل سری زمانی

حال، تنظیمات زیر را اعمال می‌کنیم:

np.random.seed(0)
plt.style.use('ggplot')

اکنون نماد (Ticker)، بازه زمانی بین داده‌ها (Interval)، تاریخ اولین داده و تاریخ آخرین داده را تعیین می‌کنیم:

Ticker = 'BTC-USD'
Interval = '1d'
Date1 = dt.datetime(2015, 1, 1)
Date2 = dt.datetime(2022, 1, 1)

حال می‌توانیم داده‌ها را به‌شکل زیر دریافت کنیم:

DF = yf.download(tickers=Ticker, interval=Interval, start=Date1, end=Date2)

به جز روش فوق، می‌توان از روش زیر نیز استفاده کرد:

Interval = '1d'
Date1 = dt.datetime(2015, 1, 1)
Date2 = dt.datetime(2022, 1, 1)

Ticker = yf.Ticker('BTC-USD')
DF = Ticker.history(interval=Interval, start=Date1, end=Date2)

همچنین می‌توان از کتابخانه Pandas Datareader نیز به‌شکل زیر برای این منظور استفاده کرد:

Ticker = 'BTC-USD'
Date1 = dt.datetime(2015, 1, 1)
Date2 = dt.datetime(2022, 1, 1)

DF = pdt.DataReader(Ticker, data_source='yahoo', start=Date1, end=Date2)

به این ترتیب، در هر سه روش، خروجی حاصل یک دیتافریم خواهد بود. توجه داشته باشید که به‌دلیل سرعت ارتباط یا قطعی ارتباط اینترنتی، ممکن است در برخی مواقع دریافت داده با مشکل مواجه شود.

فیلم آموزش پیش بینی قیمت سهام در بورس با شبکه عصبی عمیق LSTM در متلب در تم آف

کلیک کنید

برای نمایش دیتافریم حاصل، می‌نویسیم:

print(DF.head())

و به‌صورت زیر، خواهیم داشت:

                  Open        High         Low       Close   Adj Close    Volume
Date
2014-12-31  310.914001  320.192993  310.210999  320.192993  320.192993  13942900
2015-01-01  320.434998  320.434998  314.002991  314.248993  314.248993   8036550
2015-01-02  314.079010  315.838989  313.565002  315.032013  315.032013   7860650
2015-01-03  314.846008  315.149994  281.082001  281.082001  281.082001  33054400
2015-01-04  281.145996  287.230011  257.612000  264.195007  264.195007  55629100

حال نمودار شمعی (Candle Stick Plot) را در ۲۰۰ روز اخیر برای قیمت به‌صورت زیر رسم می‌کنیم:

mplf.plot(DF.iloc[-200:], type='candle')
plt.show()

به این ترتیب، نمودار به‌شکل زیر خواهد بود.

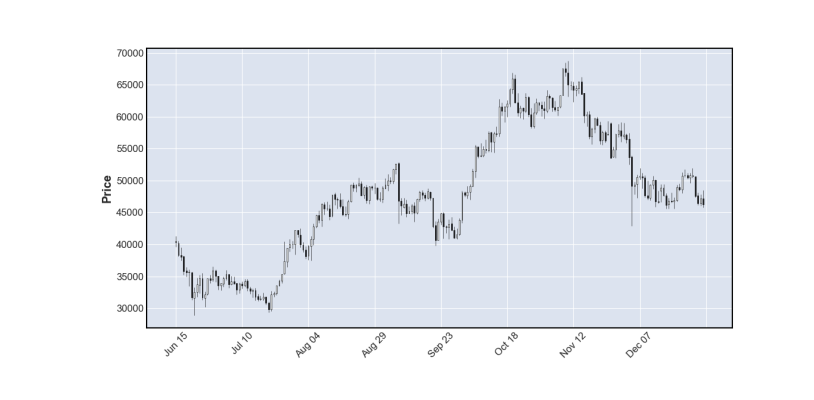
به این ترتیب، نمودار شمعی رسم می‌شود. حال می‌توانیم نمودار حجم را نیز ضافه کنیم. افزون دو میانگین متحرک با پنجره ۱۳ روز و ۵۵ روز می‌تواند روند و سطوح را به خوبی نشان دهد:

mplf.plot(DF.iloc[-200:], type='candle', mav=(13, 55), volume=True)
plt.show()

در این صورت، نمودار زیر حاصل خواهد شد.

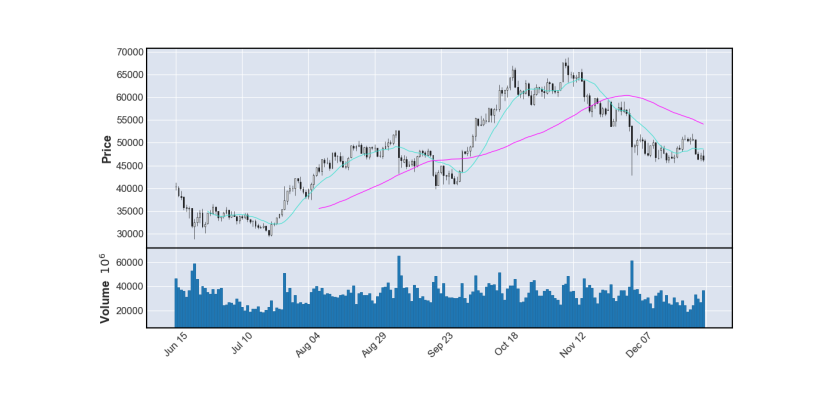
به این ترتیب، نمودارها نیز به‌خوبی رسم و رفتار سهم مشاهده می‌شود.

پیش‌پردازش داده

در مرحله اول از پیش‌بینی، تنها از داده‌های Close استفاده می‌کنیم.

فیلم آموزش تجزیه و تحلیل داده های مالی با پایتون – بخش یکم در تم آف

کلیک کنید

برای این کار ابتدا ستون مربوط به قیمت بسته شدن نماد را استخراج می‌کنیم:

C = DF['Close'].to_numpy()

سپس نمودار متغیر مورد نظر را رسم می‌کنیم:

plt.plot(C, lw=0.7, c='crimson')
plt.title('BTC Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price (USD)')
plt.show()

در خروجی کد فوق، شکل زیر را خواهیم داشت.

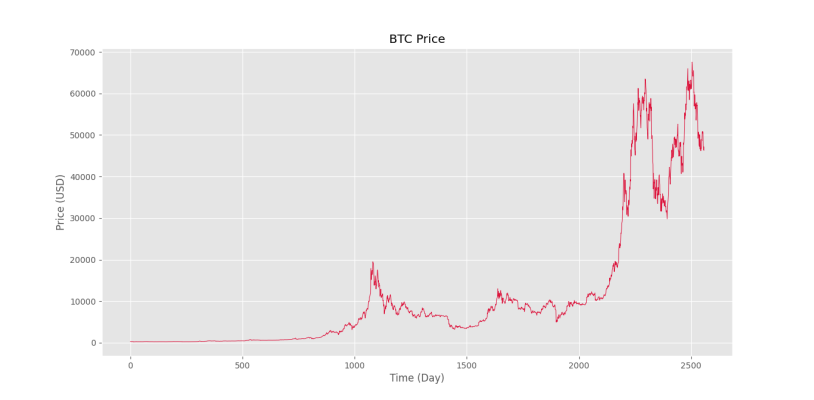
می‌بینیم که نمودار رسم شده است. به دلیل ماهیت نمایی بازار، تغییرات قیمت در ۷۰۰ روز اول به‌خوبی قابل مشاهده نیست.

فیلم آموزش پیش بینی نوسانات بازار سهام با هوش مصنوعی در پایتون Python در تم آف

کلیک کنید

برای رفع این مشکل، از قیمت لگاریتم می‌گیریم و نمودار را دوباره رسم می‌کنیم:

S = np.log(C)

plt.plot(S, lw=0.7, c='crimson')
plt.title('BTC Price Logrithm')
plt.xlabel('Time (Day)')
plt.ylabel('Log(Price (USD))')
plt.show()

و در خروجی، شکل زیر را خواهیم داشت.

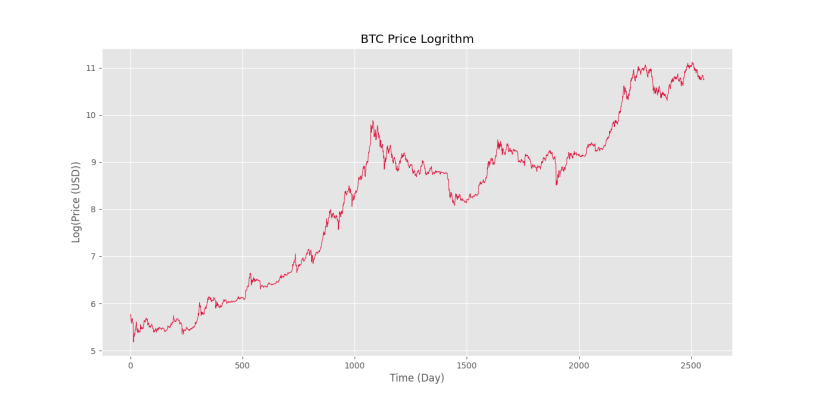
به این ترتیب، مشاهده می‌کنیم که اختلاف سطوح قیمت به‌‌خوبی رفع شده است. می‌توان برای رفع روند (Trend) سری زمانی، از روش‌هایی مانند تفاضل‌گیری، حذف روند خطی، میانگین متحرک و یا Hodrick-Prescott Filter استفاده کرد.

فیلم آموزش دریافت و پردازش دفتر سفارش در بازارهای مالی با پایتون در تم آف

کلیک کنید

حال تابع Lag را برای تولید مجموعه داده پیاده‌سازی می‌کنیم:

def Lag(S:np.ndarray, L:int):
    nD0 = S.size
    nD = nD0 - L
    X = np.zeros((nD, L))
    Y = np.zeros((nD, 1))
    for i in range(nD):
        X[i, :] = S[i:i + L]
        Y[i, 0] = S[i + L]
    return X, Y

این تابع به‌ترتیب مراحل زیر را انجام می‌دهد:

1. اندازه سری زمانی ورودی تعیین می‌شود.
2. اندازه داده خروجی تعیین می‌شود (با توجه به اینکه برای L داده موجود در ابتدای سری، نمی‌توان جفت‌های x و y تشکیل داد).
3. دو آرایه خالی برای X و Y ایجاد می‌شود.
4. به‌ازای تمامی داده‌ها، هر سطر از ماتریس‌های X و Y مقداردهی می‌شود.
5. مجموعه داده تولید شده در خروجی برگردانده می‌شود.

فیلم آموزش کاربرد پایتون در بازارهای مالی – دریافت و پردازش قیمت رمزارزها (رایگان) در تم آف

کلیک کنید

با استفاده از این تابع، سری زمانی را به مجموعه داده قابل استفاده تبدیل می‌کنیم:

nLag = 30
X0, Y0 = Lag(S, nLag)

حال می‌توانیم درصد «داده‌های آموزش» (Train Dataset) را تعیین و سپس تعداد آن‌ها را محاسبه کنیم:

sTrain = 0.8
nDtr = int(sTrain * S.size)

حال می‌توانیم داده‌ها را به دو مجموعه داده آموزش و آزمایش (Test) تقسیم کنیم:

trX0 = X0[:nDtr]
teX0 = X0[nDtr:]
trY0 = Y0[:nDtr]
teY0 = Y0[nDtr:]

به این ترتیب، داده‌ها تقسیم می‌شود. حال مقیاس داده‌ها را اصلاح می‌کنیم:

SSX = pp.StandardScaler()
trX = SSX.fit_transform(trX0)
teX = SSX.transform(teX0)

SSY = pp.StandardScaler()
trY = SSY.fit_transform(trY0)
teY = SSY.transform(teY0)

با توجه به اینکه تنها یک ویژگی هدف وجود دارد، آرایه هدف را به‌شکل زیر تغییر می‌دهیم:

trY = trY.reshape(-1)
teY = teY.reshape(-1)

پیش بینی قیمت با مدل خودهمبسته

حال برای انجام پیش‌بینی، از یک مدل «خودهمبسته» (Autoregressive) استفاده می‌کنیم. برای مطالعه بیشتر در این موضوع، می‌توانید به مطلب «مدل خودهمبسته (Autoregressive) در پایتون – راهنمای گام به گام» مراجعه کنید.

فیلم آموزش تجزیه و تحلیل داده های مالی با پایتون – بخش یکم در تم آف

کلیک کنید

اکنون می‌توانیم یک مدل خطی ایجاد کنیم و آن را آموزش دهیم:

Model = lm.LinearRegression()
Model.fit(trX, trY)

برای محاسبه معیارهای ارزیابی مدل، تابعی به‌صورت زیر تعریف می‌کنیم تا با گرفتن مدل و داده، معیارهای مورد نظر را محاسبه و در خروجی چاپ کند:

def RegressionReport(Model, X:np.ndarray, Y:np.ndarray):
    P = Model.predict(X)

    MSE = met.mean_squared_error(Y, P)
    RMSE = MSE**0.5
    NRMSE = 100 * RMSE / (np.max(Y) - np.min(Y))
    MAE = met.mean_absolute_error(Y, P)
    MAPE = 100 * met.mean_absolute_percentage_error(Y, P)
    R2 = 100 * met.r2_score(Y, P)

    print(f'MSE:   {round(MSE, 4)}')
    print(f'RMSE:  {round(RMSE, 4)}')
    print(f'NRMSE: {round(NRMSE, 2)} %')
    print(f'MAE:   {round(MAE, 4)}')
    print(f'MAPE:  {round(MAPE, 2)} %')
    print(f'R2:    {round(R2, 2)} %')

این تابع در ابتدا پیش‌بینی مدل برای داده‌ها را دریافت کرده، سپس معیارهای مختلف را با استفاده از sklearn.metrics و یا روابط موجود محاسبه می‌کند. در نهایت هر معیار چاپ می‌شود.

فیلم آموزش پیش بینی نوسانات بازار سهام با هوش مصنوعی در پایتون Python در تم آف

کلیک کنید

حال برای داده‌های آموزش و آزمایش تابع نوشته شده را اجرا می‌کنیم:

print('Model Regression Report on Train Dataset:')
RegressionReport(Model, trX, trY)
print('_'*60)
print('Model Regression Report on Test Dataset:')
RegressionReport(Model, teX, teY)

که در خروجی خواهیم داشت:

Model Regression Report on Train Dataset:
MSE:   0.0007
RMSE:  0.0273
NRMSE: 0.85 %
MAE:   0.0175
MAPE:  8.95 %
R2:    99.93 %
____________________________________________________________
Model Regression Report on Test Dataset:
MSE:   0.0008
RMSE:  0.0276
NRMSE: 2.05 %
MAE:   0.0201
MAPE:  1.06 %
R2:    99.55 %

به این ترتیب، مشاهده می‌کنیم که ضریب مدل در هر دو مجموعه داده نزدیک به هم بوده و مناسب است. توجه داشته باشید که مقدار معیار MAPE در مجموعه داده آموزش ۸ برابر بیشتراز مجموعه داده آزمایش است که شاید در ابتدا عجیب به نظر بیاید. دلیل این اتفاق وجود مقادیر نزدیک به ۰ در مجموعه داده آموزش است.

فیلم آموزش کاربرد پایتون در بازارهای مالی – دریافت و پردازش قیمت رمزارزها (رایگان) در تم آف

کلیک کنید

با توجه به رشد زیاد قیمت نماد در سال‌های اخیر، در ٪۲۰ انتهایی مجموعه داده، اعداد بزرگ‌تر از میانگین هستند و به همین دلیل، مقادیر نزدیک به ۰ اغلب در مجموعه داده آموزش قرار دارد. علاوه بر این مورد، اختلاف زیادی نیز در مقدار معیار NRMSE وجود دارد، در حالی که بین RMSEها اختلاف زیادی وجود ندارد. این اتفاق نیز به‌دلیل تفاوت در Range داده‌ها است. ٪۸۰ ابتدایی داده، شامل بازه بزرگتری (از ۵ تا ۱۰) می‌شود، درحالی‌که ٪۲۰ انتهایی شامل بازه کوچک‌تری (از ۹ تا ۱۱) می‌شود. به این دلیل، ۲٫۵ برابر بودن RMSE در مجموعه داده آموزش طبیعی است.

برای مطالعه این معیار‌ها، می‌توانید به مطلب «بررسی معیارهای ارزیابی رگرسیون در پایتون — پیاده سازی + کدها» مراجعه کنید.

رسم نمودارها

حال نمودار سری زمانی اصلی و پیش‌بینی مدل را برای داده‌های آموزش و آزمایش رسم می‌کنیم:

trP = Model.predict(trX)
teP = Model.predict(teX)

plt.plot(trY, lw=0.9, c='crimson', label='Target Values')
plt.plot(trP, lw=0.9, c='teal', label='Predicted Values')
plt.title('Model Result on Train Dataset')
plt.xlabel('Time (Day)')
plt.ylabel('Value')
plt.legend()
plt.show()

plt.plot(teY, lw=0.9, c='crimson', label='Target Values')
plt.plot(teP, lw=0.9, c='teal', label='Predicted Values')
plt.title('Model Result on Test Dataset')
plt.xlabel('Time (Day)')
plt.ylabel('Value')
plt.legend()
plt.show()

در خروجی کد فوق دو نمودار زیر حاصل می‌شوند.

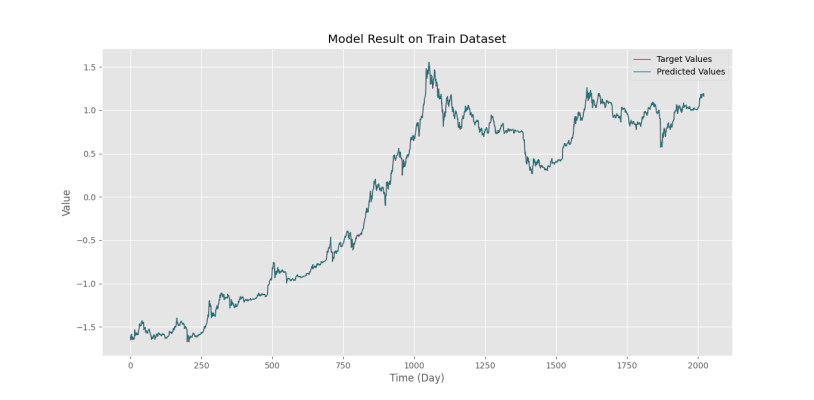
نمودار دوم در تصویر زیر آورده شده است.

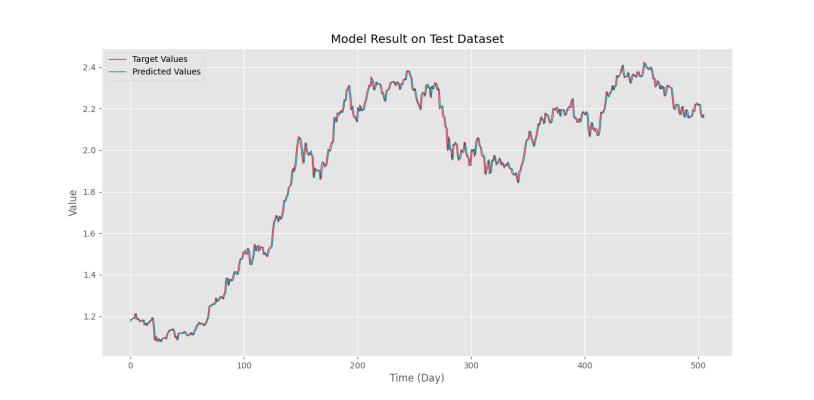
به این ترتیب، مشاهده می‌کنیم که پیش‌بینی مدل به داده‌های واقعی بسیار نزدیک است. اما نکته‌ای که وجود دارد، اندکی تأخیر مدل در پیش‌بینی است. در واقع، مدل سعی کرده تا قیمت آخرین روز را به‌عنوان پیش‌بینی فردا استفاده کند (با اندکی بهبود با استفاده از قیمت‌های گذشته).

فیلم آموزش پیش بینی قیمت سهام در بورس با شبکه عصبی عمیق LSTM در متلب در تم آف

کلیک کنید

برای مشاهده وزن مدل برای روزهای گذشته به‌شکل زیر عمل می‌کنیم:

W = Model.coef_
print(f'W:n{W}')

که خواهیم داشت:

[+3.58563953e-02 -1.96077112e-02 -1.20056042e-02
 -1.88671111e-02 +2.53669946e-02 +5.83798116e-03
 +6.07673595e-03 -1.94466868e-02 +2.97395294e-02
 -5.50333940e-02 -2.67256590e-02 +3.38254901e-02
 -3.09856605e-02 +4.98994631e-02 -6.81061580e-03
 -8.07773671e-04 +4.84668241e-03 -8.51348645e-03
 +5.97168971e-04 -4.92384255e-02 +8.77800917e-02
 -2.10080279e-02 +2.11319993e-02 -8.05356204e-02
 +2.68525320e-02 +1.56674539e-02 +2.31580583e-03
 -1.30531651e-02 +4.58633245e-02 +9.70581002e-01]

به این ترتیب، مشاهده می‌کنیم که برای روز آخر از داده‌های ورودی، وزن ۰٫۹۷ تعیین شده است که نشان از تمایل زیاد مدل به استفاده از روز آخر دارد. در واقع، مدل سعی کرده تا تغییرات برای روز بعد را محاسبه و به قیمت روز آخر اضافه کند.

برای متعادل کردن رفتار مدل، می‌توانیم از مدل‌های Ridge و Lasso و Elastic Net استفاده کنیم. توجه داشته باشید که پیش‌بینی انجام‌شده، در مقیاس تغییر یافته بود. برای تبدیل مقیاس پیش‌بینی به مقیاس اصلی داده‌ها، باید ابتدا Inverse Transform انجام شده و سپس تابع Exponential اعمال شود:

trP0 = np.exp( SSY.inverse_transform( trP.reshape( (-1, 1) ) ) )
teP0 = np.exp( SSY.inverse_transform( teP.reshape( (-1, 1) ) ) )

می‌توان برای بهبود رفتار مدل، مقدار nLag را بهینه کرد. برای این منظور، می‌توانیم نمودار تابع خودهمبستگی جزئی (Partial Autocorrelation Function – PACF) را رسم کنیم:

tsaplt.plot_pacf(S, lags=500, c='teal', lw=0.4, markersize=1)
plt.xlabel('Lags (Days)')
plt.ylabel('Pearson Correlation Coefficient')
plt.show()

که نمودار زیر حاصل می‌شود.

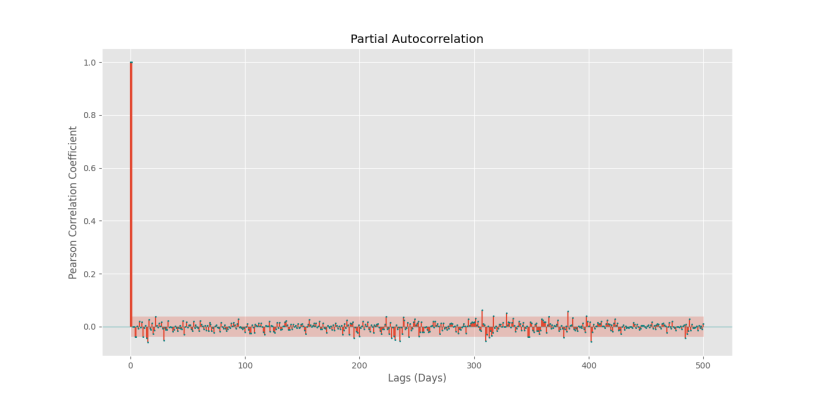
به این ترتیب، مشاهده می‌کنیم که Lagهای زیر نیز ارتباط معناداری را نشان می‌دهند:

$$ text{Lags}={1,4,5,14,15,29,195} $$

بنابراین، مشاهده می‌کنیم که در ۳۰ تأخیر ابتدایی، تنها ۶ تأخیر معنادار هستند. به این ترتیب، می‌توان تنها ۲۹ تأخیر ابتدایی را استفاده و دقت نسباً خوبی دریافت کرد. توجه داشته باشید که می‌توان به‌جای تمامی تأخیرهای بین ۱ تا ۲۹، می‌توان به‌صورت گزینشی تنها از تأخیرهای ۱ و ۴ و ۵ و ۱۴ و ۱۵ و ۲۹ استفاده کرد.

فیلم آموزش تجزیه و تحلیل داده های مالی با پایتون – بخش یکم در تم آف

کلیک کنید

جمع‌بندی پیش بینی قیمت در پایتون

در این مطلب، از رگرسیون خطی برای پیش بینی قیمت در پایتون برای روز بعد استفاده کردیم.

برای مطالعه بیشتر، می‌توان موارد زیر را بررسی کرد:

1. تابع Lag را به‌صورتی تغییر دهید که Lagها را به‌صورت گزینشی به مجموعه داده اضافه کند.
2. وجود تأخیر‌های غیرمعنادار در ویژگی‌های ورودی، باعث چه مشکلاتی می‌شود؟
3. آیا می‌توان به جای انتخاب ٪۸۰ داده برای آموزش از ابتدای سری زمانی، آن را به‌صورت تصادفی از کل سری زمانی انتخاب کرد؟
4. در بخش پیش‌پردازش سری زمانی، از یکی از روش‌های گفته‌شده برای حذف روند استفاده و نتایج را مقایسه کنید.
5. مدل‌های KNN و SVM و MLP را روی مجموعه داده آموزش داده و نتایج را مقایسه کنید.
6. اگر بخواهیم به‌جای پیش‌بینی مقدار قیمت در روز بعد، جهت تغییرات را در سه دسته افزایش، کاهش و خنثی پیش‌بینی کنیم، کد را باید به چه صورتی تغییر دهیم؟