پیش بینی جهت قیمت در پایتون — راهنمای کاربردی

در مطالب گذشته مجله تم آف، به پیشبینی قیمت در پایتون پرداختیم و با استفاده از یک مدل رگرسیون خطی (Linear Regression)، مقدار قیمت را پیشبینی کردیم. در این مطلب، قصد داریم به جای پیشبینی مقدار قیمت در آینده، به پیش بینی جهت قیمت در پایتون بپردازیم که یک مسئله طبقهبندی (Classification) خواهد بود.

پیش بینی جهت قیمت در پایتون
برای شروع کدنویسی، کتابخانههای مورد نیاز را فراخوانی میکنیم:
import numpy as np
import yfinance as yf
import sklearn.dummy as dm
import sklearn.metrics as met
import matplotlib.pyplot as plt
import sklearn.linear_model as lm
import sklearn.preprocessing as ppاز این ۷ کتابخانه به ترتیب برای موارد زیر استفاده خواهیم کرد:
- محاسبات برداری
- دریافت برخط (Online) مجموعه داده تاریخی (Historical Dataset)
- ایجاد و آموزش Dummy Classifier
- محاسبه معیارهای ارزیابی برای مدل
- رسم نمودار
- ایجاد و آموزش مدل رگرسیون لجستیک (Logistic Regression)
- پیشپردازش داده
برای مطالعه بیشتر در مورد رگرسیون لجستیک، میتوانید به مطلب «پیاده سازی رگرسیون لجستیک در پایتون – راهنمای گام به گام» مراجعه کنید.
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است. حال تنظیمات مورد نیاز را اعمال میکنیم:
np.random.seed(0)
plt.style.use('ggplot')حال مجموعه داده مربوط به کل تاریخچه روزانه نماد ETH/USD را دریافت میکنیم:
Ticker = 'ETH-USD'
Interval = '1d'
Period = 'max'
DF = yf.download(tickers=Ticker, interval=Interval, period=Period)اکنون مجموعه داده را بررسی میکنیم که تا از صحت آن مطمئن شویم:
print(DF.head())
print(DF.tail())که خواهیم داشت:
Open High Low Close Adj Close Volume Date 2017-11-09 308.644989 329.451996 307.056000 320.884003 320.884003 893249984 2017-11-10 320.670990 324.717987 294.541992 299.252991 299.252991 885985984 2017-11-11 298.585999 319.453003 298.191986 314.681000 314.681000 842300992 2017-11-12 314.690002 319.153015 298.513000 307.907990 307.907990 1613479936 2017-11-13 307.024994 328.415009 307.024994 316.716003 316.716003 1041889984 Open High Low Close Adj Close Volume Date 2022-03-14 2518.486328 2604.034424 2505.299316 2590.696045 2590.696045 11244398839 2022-03-15 2590.668945 2662.329590 2515.765869 2620.149658 2620.149658 12861105614 2022-03-16 2620.028564 2781.307129 2610.764404 2772.055664 2772.055664 17915109769 2022-03-17 2771.964111 2826.160645 2751.560791 2814.854492 2814.854492 12685265194 2022-03-18 2812.546631 2812.546631 2775.212402 2800.633301 2800.633301 12803630080
به این ترتیب، از صحت دادهها مطمئن میشویم. حال میتوانیم درصد تغییرات نسبی در هر روز را محاسبه کنیم:
DF['RPC'] = 100 * (DF['Close'] / DF['Open'] - 1)حال میتوانیم یک نمودار هیستوگرام (Histogram Plot) برای این متغیر رسم کنیم:
plt.hist(DF['RPC'], bins=41, color='b', alpha=0.6)
plt.title('ETH-USD Relative Percentage Change')
plt.xlabel('Relative Change (%)')
plt.ylabel('Frequency')
plt.show()که در خروجی، شکل زیر را خواهیم داشت.
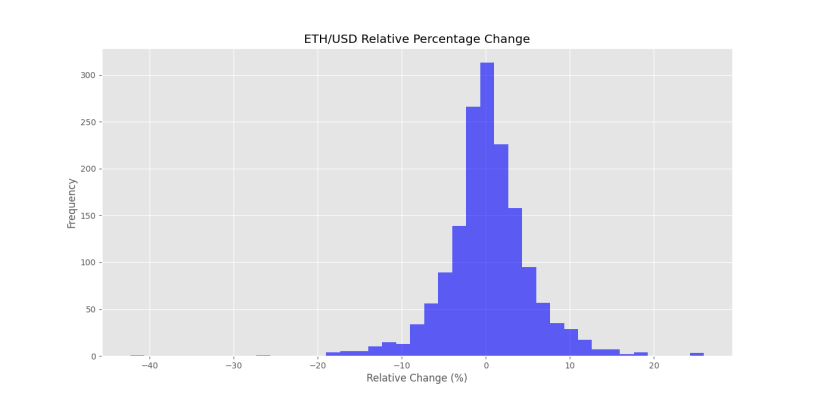
به این ترتیب، یک توزیع نرمال مشاهده میشود. حال میتوانیم با استفاده از روش دامنه میان چارکی (Interquartile Rage) مقادیر پرت (Outlier) را اصلاح کنیم:
k = 1.5
q1 = DF['RPC'].quantile(0.25)
q3 = DF['RPC'].quantile(0.75)
iqr = q3 - q1
lb = q1 - k * iqr
ub = q3 + k * iqr
DF['RPC'] = DF['RPC'].clip(lower=lb, upper=ub)حال اگر دوباره نمودار هیستوگرام را تکرار کنیم، شکل زیر را خواهیم داشت.
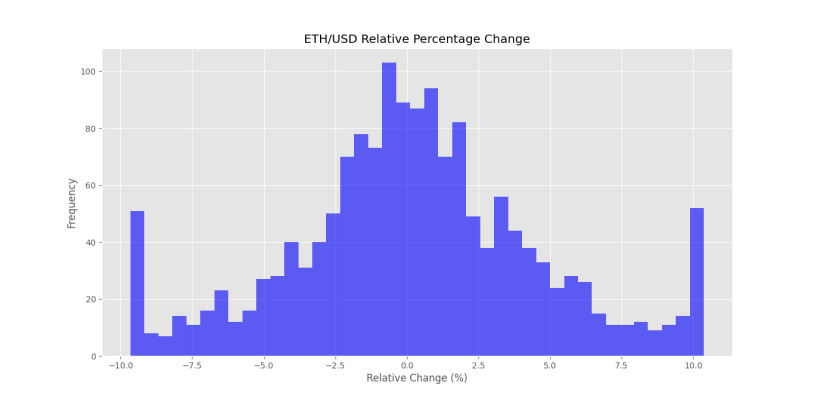
توجه داشته باشید که انباشت دادهها در دو ستون ابتدایی و انتهایی مشاهده میشود که به دلیل اصلاح آن دادهها است.
برای رفع این مشکل، میتوان از روشهای دیگری برای اصلاح دادههای پرت استفاده کرد. توجه داشته باشید که با افزایش مقدار k از ۱٫۵ به ۲، نتایج را به شکل زیر تغییر میدهد.
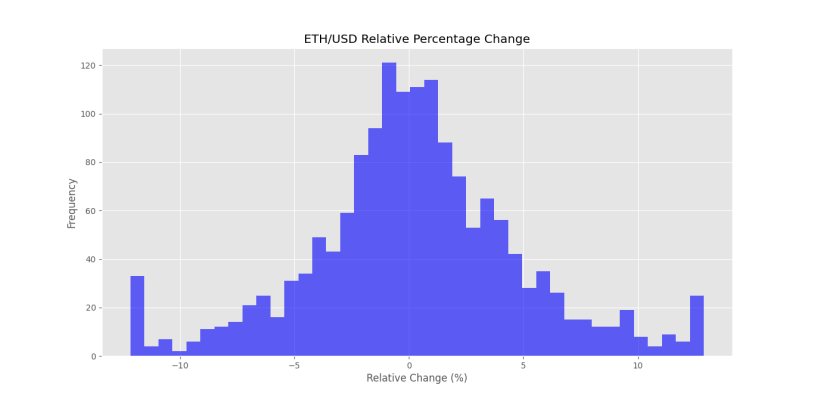
به این ترتیب، مشاهده میکنیم اندکی نتایج بهبود یافته است.
حال میتوانیم دادههای ستون RPC را به صورت آرایه دریافت کنیم:
S = DF['RPC'].to_numpy()اکنون تابع Lag را وارد برنامه میکنیم:
def Lag(S:np.ndarray, L:int):
nD0 = S.size
nD = nD0 - L
X = np.zeros((nD, L))
Y = np.zeros((nD, 1))
for i in range(nD):
X[i, :] = S[i:i + L]
Y[i, 0] = S[i + L]
return X, Yو برای استفاده از آن، به شکل زیر عمل میکنیم:
nLag = 30
X0, Y0 = Lag(S, nLag)به این ترتیب، دادههای اولیه حاصل میشود. حال دادهها را به دو مجموعه داده آموزش (Train Dataset) و آزمایش (Test Dataset) تقسیم میکنیم:
sTrain = 0.8
nDtr = int(sTrain * X0.shape[0])
trX0 = X0[:nDtr]
teX0 = X0[nDtr:]
trY0 = Y0[:nDtr]
teY0 = Y0[nDtr:]با توجه به اینکه درصد تغییرات نسبی، مقیاس مناسبی ارائه نمیدهد، مقیاس آنها را به شکل زیر اصلاح میکنیم:
SSX = pp.StandardScaler()
trX = SSX.fit_transform(trX0)
teX = SSX.transform(teX0)برای مقادیر ویژگی هدف، باید یک تابع گسستهساز (Discretizer) تعریف کنیم و مقادیر را در کلاس مربوط به خود قرار دهیم. برای این کار معمولاً ۳ دسته در نظر میگیرم:
- کاهش
- خنثی
- افزایش
برای این کار، یک مقدار مرزی (Threshold) تعریف میکنیم:
- اگر تغییرات کمتر از قرینه Threshold بود، کاهش قیمت رخ داده است. (دسته ۰)
- اگر تغییرات بیشتر از Threshold بود، افزایش قیمت رخ داده است. (دسته ۲)
- در غیر این صورت، تغییرات خنثی بوده است. (دسته ۱)
برای این کار، یک تابع Discretizer تعریف میکنیم که در ورودی ماتریس Y0 و مقدار Threshold را دریافت میکند:
def Discretizer(Y0:np.ndarray, TH:float):ابتدا اندازه داده را محاسبه میکنیم:
def Discretizer(Y0:np.ndarray, TH:float):
nD = Y0.sizeحال یک ماتریس خالی برای ذخیره دسته هر داده ایجاد میکنیم:
def Discretizer(Y0:np.ndarray, TH:float):
nD = Y0.size
Y = np.zeros((nD, 1))حال میتوانیم یک حلقه ایجاد کرده و برای هر داده، شرطهای گفته شده را بررسی کنیم:
def Discretizer(Y0:np.ndarray, TH:float):
nD = Y0.size
Y = np.zeros((nD, 1))
for i in range(nD):
if Y0[i] +TH:
Y[i, 0] = 2
else:
Y[i, 0] = 1
return Yبه این ترتیب، تابع مد نظر پیادهسازی میشود. برای اندکی سادهسازی این تابع، میتوان به شکل زیر نوشت:
def Discretizer(Y0:np.ndarray, TH:float):
nD = Y0.size
Y = np.ones((nD, 1))
for i in range(nD):
if Y0[i] +TH:
Y[i, 0] = 2
return Yبه این ترتیب، تابع مورد نظر پیادهسازی شد. حال برای استفاده از تابع، به شکل زیر مینویسیم:
TH = 2
trY = Discretizer(trY0, TH)
teY = Discretizer(teY0, TH)توجه داشته باشید که در خروجی کد فوق، تغییرات بین ۲- و ۲+ به عنوان حرکات خنثی در نظر گرفته میشود. تنظیم مقدار TH بسیار حائز اهمیت است.
حال برای استفاده از ماتریس Y برای آموزش و آزمایش مدل، آنها را به شکل تکبُعدی تغییر میدهیم:
trY = trY.reshape(-1)
teY = teY.reshape(-1)اکنون میتوانیم مدل رگرسیون لجستیک را ایجاد کرده و آموزش دهیم:
Model = lm.LogisticRegression()
Model.fit(trX, trY)حال میتوانیم برای دادههای آموزش و آزمایش پیشبینیهای مدل را دریافت کنیم:
trPr = Model.predict(trX)
tePr = Model.predict(teX)اکنون میتوانیم گزارش طبقهبندی را به شکل زیر محاسبه و نمایش دهیم:
trCR = met.classification_report(trY, trPr)
teCR = met.classification_report(teY, tePr)
print(f'Train Classification Report:n{trCR}')
print('_'*60)
print(f'Test Classification Report:n{teCR}')که در خروجی خواهیم داشت:
Train Classification Report: precision recall f1-score support 0.0 0.46 0.09 0.16 321 1.0 0.49 0.86 0.62 561 2.0 0.44 0.23 0.31 366 accuracy 0.48 1248 macro avg 0.46 0.40 0.36 1248 weighted avg 0.47 0.48 0.41 1248 ______________________________________________________ Test Classification Report: precision recall f1-score support 0.0 0.32 0.07 0.12 96 1.0 0.38 0.78 0.51 115 2.0 0.27 0.14 0.18 102 accuracy 0.35 313 macro avg 0.32 0.33 0.27 313 weighted avg 0.32 0.35 0.28 313
به این ترتیب، مشاهده میکنیم که F1 Score Macro Average برای دادههای آموزش ۰٫۳۶ و برای دادههای آزمایش ۰٫۲۷ است که نتایج نهچندان مطلوبی است. بخشی از این مشکل، از نامتعادل بودن مجموعه داده نشأت میگیرد که در مطالب «متعادل کردن داده در پایتون – بخش اول: وزن دهی دسته ها» و «متعادل کردن داده در پایتون – بخش دوم: تغییر مجموعه داده» به روشهایی برای رفع آن پرداخته شده است.
برای رفع این مشکل، وزن هر دسته را به شکل زیر محاسبه میکنیم:
nClass = 3
nTotal = trY.size
Ns = {i: trY[trY == i].size for i in range(nClass)}
W = {i: (nTotal - Ns[i])/((nClass - 1) * nTotal) for i in range(nClass)}حال میتوانیم دیکشنری وزن را به شکل زیر در تعریف مدل استفاده کنیم:
Model = lm.LogisticRegression(class_weight=W)پس از آموزش مدل و تکرار فرآیند، گزارشهای زیر حاصل میشود:
Train Classification Report: precision recall f1-score support 0.0 0.39 0.25 0.30 321 1.0 0.51 0.65 0.57 561 2.0 0.41 0.37 0.39 366 accuracy 0.47 1248 macro avg 0.44 0.42 0.42 1248 weighted avg 0.45 0.47 0.45 1248 _____________________________________________________ Test Classification Report: precision recall f1-score support 0.0 0.31 0.20 0.24 96 1.0 0.34 0.50 0.40 115 2.0 0.27 0.22 0.24 102 accuracy 0.31 313 macro avg 0.30 0.30 0.29 313 weighted avg 0.31 0.31 0.30 313
به این ترتیب، مشاهده میکنیم که F1 Score Macro Average برای دادههای آموزش و آزمایش به ترتیب برابر ۰٫۴۲ و ۰٫۲۹ میشود. به این ترتیب، مشاهده میکنیم که ۰٫۰۶ واحد در مجموعه داده آموزش و ۰٫۰۲ واحد در مجموعه داده آزمایش بهبود رخ داده است.
برای درک بهتر این دقتها، میتوان یک Dummy Classifier آموزش داد و نتایج آن را با مدلِ آموزشدیده مقایسه کرد:
Dummy = dm.DummyClassifier(strategy='most_frequent')
Dummy.fit(trX, trY)
trPr = Dummy.predict(trX)
tePr = Dummy.predict(teX)
trF1ScoreMA = met.f1_score(trY, trPr, average='macro')
teF1ScoreMA = met.f1_score(teY, tePr, average='macro')
print(f'Dummy Train F1 Score Macro Average: {trF1ScoreMA}')
print(f'Dummy Test F1 Score Macro Average: {teF1ScoreMA}')که برای این مدل نتایج زیر حاصل میشود:
Dummy Train F1 Score Macro Average: 0.20674405749032612 Dummy Test F1 Score Macro Average: 0.17798594847775176
به این ترتیب، مشاهده میکنیم که نتایج رگرسیون لجستیک خیلی بهتر از Dummy Classifier است. اما حتماً باید توجه کرد دقتهای حاصلشده بهاندازهای خوب نیستند که قابل اعتماد باشند.
نکته دیگری که باید به آن اشاره کرد، پیچیدگی موجود در داده است. دادههای مالی در ذات خود پیچیدگی بالایی دارند و سری زمانی بودن آنها، بر این پیچیدگی میافزاید. به همین دلیل، باید به نکات ریز موجود در پردازش داده، انتخاب مدل و تنظیم مدل توجه کرد.
برای دست یافتن به دقتهای بالاتر، میتوان مدلهایی دیگر را مقایسه کرد. در زیر، مثالهایی از این مدلها آورده شده است:
- K-نزدیکترین همسایه (K-Nearest Neighbors – KNN)
- جنگل تصادفی (Random Forest – RF)
- پرسپترون چند لایه (Multi-Layer Perceptron – MLP)
- ماشین بردار پشتیبان (Support Vector Machine – SVM)
جمعبندی پیش بینی جهت قیمت در پایتون
در این مطلب، بحث پیش بینی جهت قیمت برای دادههای مالی را بررسی کردیم.
برای مطالعه بیشتر، میتوان موارد زیر را بررسی کرد:
- هرکدام از مدلهای معرفی شده را بررسی کرده و دقت هرکدام را محاسبه کنید.
- چه اشکالاتی ممکن است در پیشپردازش دادهها وجود داشته باشد؟
- اگر داده را به جای ۳ دسته، به ۵ دسته تقسیم کنیم، تابع Discretizer به چه شکل تغییر خواهد کرد؟
- بین F1 Score و Accuracy کدامیک بیشتر قابل اعتماد است؟ چرا؟
- بین Macro Average و Weighted Average کدامیک بیشتر قابل اعتماد است؟ چرا؟

