پیاده سازی میانگین متحرک نمایی در پایتون — راهنمای گام به گام

در آموزشهای قبلی مجله تم آف، با پیادهسازی میانگین متحرک ساده در پایتون آشنا شدیم و به برخی از نقاط ضعف آن اشاره کردیم. در این آموزش، به میانگین متحرک نمایی (Exponential Moving Average) یا EMA خواهیم پرداخت. در این روشِ میانگینگیری، برخلاف روش ساده، با تمامی دادهها به یک شکل برخورد نمیکنیم و به دادههای جدیدتر، وزن زیادی قائل میشویم. این ویژگی باعث میشود تا تأخیر کمتری در رفتار آن وجود داشته باشد. در ادامه، به پیاده سازی میانگین متحرک نمایی در پایتون میپردازیم.

میانگین متحرک نمایی چیست؟
اگر یک سری زمانی به شکل زیر داشته باشیم:
$$ large X =left{x_{1}, x_{2} ldots x_{n}right} $$
یک میانگین متحرک نمایی با طول $$L$$ به شکل زیر محاسبه میشود:
$$ large begin{aligned}
&M_{L}=frac{1}{L} sum_{i=1}^{L} x_{i}\
&M_{t}=alpha cdot x_{t}+(1-alpha) cdot M_{t-1} quad L
end{aligned} $$
به این ترتیب، مقدار در هر زمان با توجه به زمانهای قبلی محاسبه میشود.
به سادگی میتوانیم وزن مربوط به هر روز را به شکل زیر محاسبه کنیم:
$$ large begin{aligned}
&W_{t}=alpha\
&W_{t-1}=alpha cdot(1-alpha)\
&W_{t-2}=alpha cdot(1-alpha)^{2}\
&vdots \
&W_{t-infty}=alpha cdot(1-alpha)^{infty}=0
end{aligned} $$
که مجموع وزنها به صورت زیر خواهد بود:
$$ large begin{align}
text { Sum } & =sum_{i=0}^{infty} W_{t-i}=sum_{i=0}^{infty} alpha cdot(1-alpha)^{i}=alpha sum_{i=0}^{infty}(1-alpha)^{i}=alpha cdotleft(frac{1}{1-(1-alpha)}right) \
& =alpha cdotleft(frac{1}{alpha}right)=1
end{align} $$
بنابراین اثبات میشود که مجموع وزنها برابر $$1$$ است.
ضریب $$alpha$$ میزان حساسیت بر دادههای جدید را تعیین میکند. اگر $$alpha = 0 $$، مقدار میانگین متحرک همواره ثابت خواهد بود و اگر $$alpha = 1 $$، مقدار میانگین متحرک همواره برابر آخرین مقدار سیگنال خواهد بود.
معمولاً به منظور محاسبه میانگین متحرک نمایی با طول $$L$$ از رابطه زیر استفاده میکنیم:
$$ large alpha =frac {1 +r } { L + r}$$
که در این رابطه اغلب حالت $$r=1$$ در نظر گرفته میشود. با افزایش $$r$$ وزن مربوط به روزهای اخیر افزایش مییابد.
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
پیادهسازی میانگین متحرک نمایی در پایتون
برای پیادهسازی میانگین متحرک نمایی، وارد محیط برنامهنویسی شده و کتابخانههای مورد نیاز را فراخوانی میکنیم:
import numpy as np
import matplotlib.pyplot as pltاین دو کتابخانه برای کار با آرایه و مصورسازی استفاده خواهند شد.
حال Style مربوط به نمودارها را نیز تنظیم میکنیم:
plt.style.use('ggplot')حال یک مجموعه داده مصنوعی به شکل زیر تولید میکنیم:
N = 200 # Signal Size
T = np.linspace(0, 80, num=N) # Time
S = 5*np.sin(8 + T/7) - 3*np.sin(5 + T/5) + 2*np.sin(3 + T/3) - np.sin(2 + T/2)برای بررسی نمودار سیگنال ایجاد شده، یک Line Plot ایجاد میکنیم:
plt.plot(T, S, ls='-', lw=1, marker='o', ms=2, label='Signal')
plt.axhline(lw=1.2, c='k')
plt.axvline(lw=1.2, c='k')
plt.xlabel('T')
plt.ylabel('Value')
plt.legend()
plt.show()که در خروجی فوق نمودار زیرحاصل میشود.
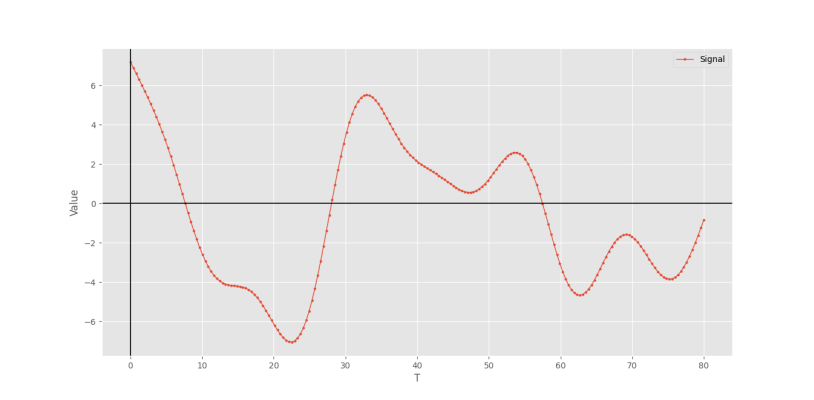
حال برای پیادهسازی میانگین متحرک نمایی، ابتدا یک تابع ایجاد میکنیم و در ورودی سیگنال، طول بازه و مقدار $$r$$ را دریافت میکنیم:
def EMA(S:np.ndarray, L:int, r:float=1):حال مقدار $$alpha$$ را محاسبه میکنیم:
def EMA(S:np.ndarray, L:int, r:float=1):
a = (1 + r) / (L + r)توجه داشته باشید که چون غالباً حالت $$r=1$$ استفاده میشود، مقدار پیشفرض برای این ورودی تعریف شده است.
حال ابتدا اندازه سیگنال را تعیین کرده و سپس اندازه میانگین متحرک حاصل را محاسبه میکنیم:
def EMA(S:np.ndarray, L:int, r:float=1):
a = (1 + r) / (L + r)
nD0 = S.size
nD = nD0 - L + 1حال یک آرایه خالی برای ذخیره مقادیر میانگین متحرک ایجاد میکنیم:
def EMA(S:np.ndarray, L:int, r:float=1):
a = (1 + r) / (L + r)
nD0 = S.size
nD = nD0 - L + 1
M = np.zeros(nD)حال اولین مقدار را به صورت میانگین معمولی از $$L$$ داده ابتدایی محاسبه میکنیم:
def EMA(S:np.ndarray, L:int, r:float=1):
a = (1 + r) / (L + r)
nD0 = S.size
nD = nD0 - L + 1
M = np.zeros(nD)
M[0] = np.mean(S[:L])حال میتوانیم سایر مقادیر را داخل یک حلقه با استفاده از رابطه بازگشتی محاسبه کنیم:
def EMA(S:np.ndarray, L:int, r:float=1):
a = (1 + r) / (L + r)
nD0 = S.size
nD = nD0 - L + 1
M = np.zeros(nD)
M[0] = np.mean(S[:L])
for i in range(1, nD):
M[i] = a*S[i+L-1] + (1-a)*M[i-1]
return Mبه این ترتیب، مقادیر بعدی محاسبه، در آرایه $$M$$ ذخیره و در خروجی برگردانده میشوند.
برای استفاده از تابع به صورت زیر عمل میکنیم:
M = EMA(S, 5)برای مشاهده رفتار میانگین متحرک حاصل، به شکل زیر نموداری رسم میکنیم:
plt.plot(T, S, ls='-', lw=1, marker='o', ms=2, label='Signal')
plt.plot(T[-M.size:], M, ls='-', lw=0.9, c='teal', label='EMA(5)')
plt.axhline(lw=1.2, c='k')
plt.axvline(lw=1.2, c='k')
plt.xlabel('T')
plt.ylabel('Value')
plt.legend()
plt.show()توجه داشته باشید که طول آرایه $$M$$ کوتاهتر از $$T$$ است. به همین دلیل، برای رسم نمودار باید تعدادی از اعضای ابتدایی آرایه $$T$$ حذف شود.
پس از اجرا، نمودار زیر نمایش داده میشود.
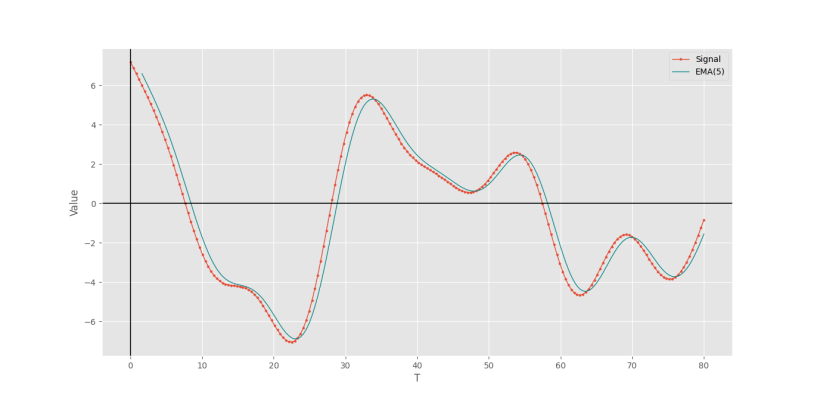
به این ترتیب، مشاهده میکنیم که تابع نوشته شده به خوبی عملکرد خود را نشان میدهد.
با افزایش مقدار $$L$$، تأخیر افزایش و در کنار آن، اعتبار نیز افزایش مییابد.
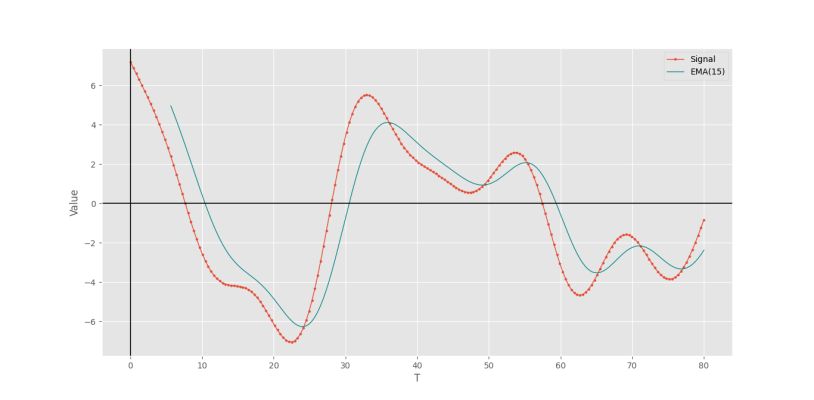
به این ترتیب، اثر $$L$$ مشهود است.
برای بررسی اثر $$r$$ نیز به شکل زیر عمل میکنیم:
M1 = EMA(S, 7, r=-0.90)
M2 = EMA(S, 7, r=0)
M3 = EMA(S, 7, r=+3)
plt.plot(T, S, ls='-', lw=1, marker='o', ms=2, label='Signal')
plt.plot(T[-M1.size:], M1, ls='-', lw=0.9, c='teal', label='EMA(5, r=-0.90)')
plt.plot(T[-M2.size:], M2, ls='-', lw=0.9, c='crimson', label='EMA(5, r=0)')
plt.plot(T[-M3.size:], M3, ls='-', lw=0.9, c='lime', label='EMA(5, r=+3)')
plt.axhline(lw=1.2, c='k')
plt.axvline(lw=1.2, c='k')
plt.xlabel('T')
plt.ylabel('Value')
plt.legend()
plt.show()که نمودار زیر برای کد فوق حاصل خواهد شد.
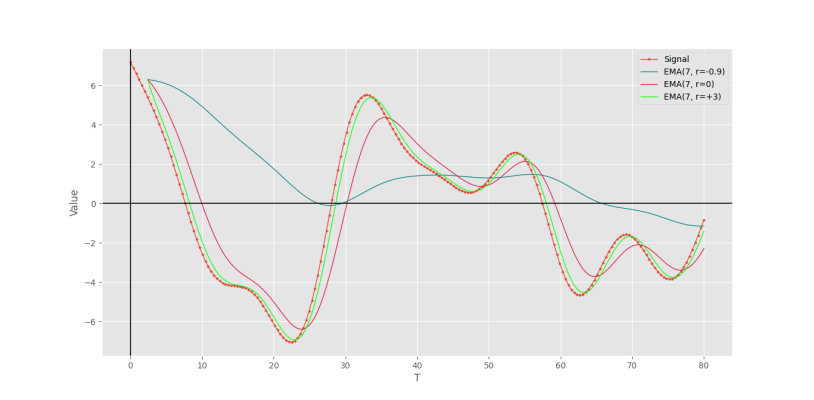
به این ترتیب، مشاهده میکنیم که در حالت $$r=-0.9$$ مقدار تأخیر به شدت افزایش یافته است. حالتهای $$r=0$$ و $$r= 3 $$ هر دو از شرایط مناسبی برخوردار هستند و هر کدام بسته به نیاز میتوانند استفاده شوند. تنظیم دو پارامتر $$L$$ و $$r$$ میتواند میانگین متحرک نمایی متناسب با نیاز ما را ایجاد کند.
حال برای مقایسه رفتار میانگین متحرک نمایی و میانگین متحرک ساده، تابع نوشته شده برای میانگین متحرک ساده را وارد کد میکنیم:
def SMA(S:np.ndarray, L:int):
nD0 = S.size
nD = nD0 - L + 1
M = np.zeros(nD)
for i in range(nD):
M[i] = np.mean(S[i:i + L])
return Mحال هر دو میانگین متحرک را در طول $$L=15$$ محاسبه میکنیم:
sma = SMA(S, 15)
ema = EMA(S, 15)و برای رسم نمودار مناسب مینویسیم:
plt.plot(T, S, ls='-', lw=1, marker='o', ms=2, label='Signal')
plt.plot(T[-sma.size:], sma, ls='-', lw=0.9, c='teal', label='SMA(15)')
plt.plot(T[-ema.size:], ema, ls='-', lw=0.9, c='lime', label='EMA(15)')
plt.axhline(lw=1.2, c='k')
plt.axvline(lw=1.2, c='k')
plt.xlabel('T')
plt.ylabel('Value')
plt.legend()
plt.show()که در نهایت نمودار مورد نظر حاصل میشود.
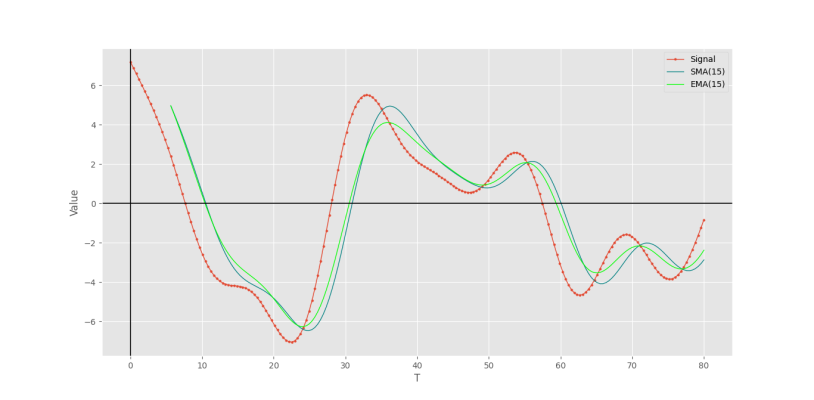
به این ترتیب، مشاهده میکنیم که میانگین متحرک نمایی زودتر از میانگین متحرک ساده به تغییرات روند واکنش میدهد.
جمعبندی
در این آموزش، میانگین متحرک نمایی در پایتون را مورد بررسی قرار دادیم. برای مطالعه بیشتر میتوان موارد زیر را بررسی کرد:
- حذف روند از سیگنال (Detrending) با استفاده از میانگین متحرک نمایی
- بررسی اختلاف بین دو میانگین متحرک نمایی با طولهای متفاوت و ارتباط آن با رفتار سیگنال
- آموزش دادن یک مدل خودهمبسته (Autoregressive) روی سیگنال و میانگین متحرک حاصل از آن و مقایسه دقتها
- پیدا کردن روشهایی که میتوان تأخیر میانگین متحرک نمایی را بیشتر از مقدار موجود کاهش داد
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش پیادهسازی انواع میانگین های متحرک در پایتون» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- میانگین متحرک چیست؟ + پیاده سازی Moving Average در پایتون
- پیاده سازی میانگین متحرک نمایی در پایتون — راهنمای گام به گام(همین مطلب)
- میانگین متحرک نمایی دوگانه و سه گانه در پایتون — راهنمای گام به گام
- میانگین متحرک وزن دار در پایتون — راهنمای گام به گام
- پیاده سازی میانگین متحرک هال در پایتون — راهنمای گام به گام

