پیاده سازی میانگین متحرک نمایی بدون تاخیر در پایتون — راهنمای گام به گام

در مطالب گذشته مجله تم آف به انواعی از میانگین متحرک‌ پرداختیم که هرکدام با یک روش، سعی در کمینه کردن تأخیر و واکنش بهتر داشتند. در این مطلب به میانگین متحرک نمایی بدون تأخیر (Zero-Lag Exponential Moving Average | ZLEMA) می‌پردازیم که با رویکردی متفاوت، بهبود داده شده است.

میانگین متحرک نمایی بدون تأخیر

در این میانگین متحرک، مجموعه داده ورودی تغییر می‌یابد؛ به بیانی دیگر، ابتدا در سطح داده، تغییراتی ایجاد می‌کنیم که در نهایت با اعمال میانگین متحرک نمایی (Exponential Moving Average | EMA)، خروجی روی داده‌های اولیه منطبق می‌شود.

فیلم آموزش تجزیه و تحلیل داده های مالی با پایتون – بخش یکم در تم آف

کلیک کنید

اگر مجموعه داده اولیه به شکل زیر باشد:

$$X={x_1,x_2…x_n }$$

با تعیین یک $$L$$ برای میانگین متحرک، مقدار $$d$$ را محاسبه می‌کنیم:

$$ d = frac {L-1} 2 $$

سپس یک سری زمانی جدید به شکل زیر محاسبه می‌کنیم:

$$S_t=X_t+(X_t-X_{t-d} )$$

توجه داشته باشید که، در واقع، با این تغییر، قیمت در لحظه فعلی، به اندازه تغییر در $$d$$ روز گذشته، تغییر می‌کند.

حال می‌توانیم یک میانگین متحرک نمایی روی سری زمانی حاصل اعمال کنیم:

$$ZLEMA_t=EMA_t (S,L)$$

فیلم آموزش پیاده سازی اندیکاتورهای تکنیکال با پایتون Python – بخش یکم در تم آف

کلیک کنید

پیاده‌سازی میانگین متحرک نمایی بدون تأخیر در پایتون

برای پیاده‌سازی، ابتدا کتابخانه‌های مورد نیاز را فراخوانی می‌کنیم:

import numpy as np
import pandas_datareader as pdt
import matplotlib.pyplot as plt

سپس تنظیمات مورد نیاز را اعمال می‌کنیم:

plt.style.use('ggplot')

حال برای شروع، مجموعه داده مربوط به تاریخچه قیمت ۲ سال اتریوم (Ethereum) را دریافت می‌کنیم:

DF = pdt.DataReader('ETH-USD',
                     data_source='yahoo',
                     start='2020-01-01',
                     end='2022-01-01')

حال ستون مربوط به قیمت پایانی (Close Price) را به شکل آرایه Numpy استخراج می‌کنیم:

Closes = DF['Close'].to_numpy()

حال می‌توانیم نمودار قیمت را به شکل نیمه‌لگاریتمی (Semi-Logarithm) رسم می‌کنیم:

plt.semilogy(Closes, ls='-', lw=0.8, c='crimson')
plt.title('ETH Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.show()

پس از اجرای کد فوق، نمودار زیر حاصل می‌شود.

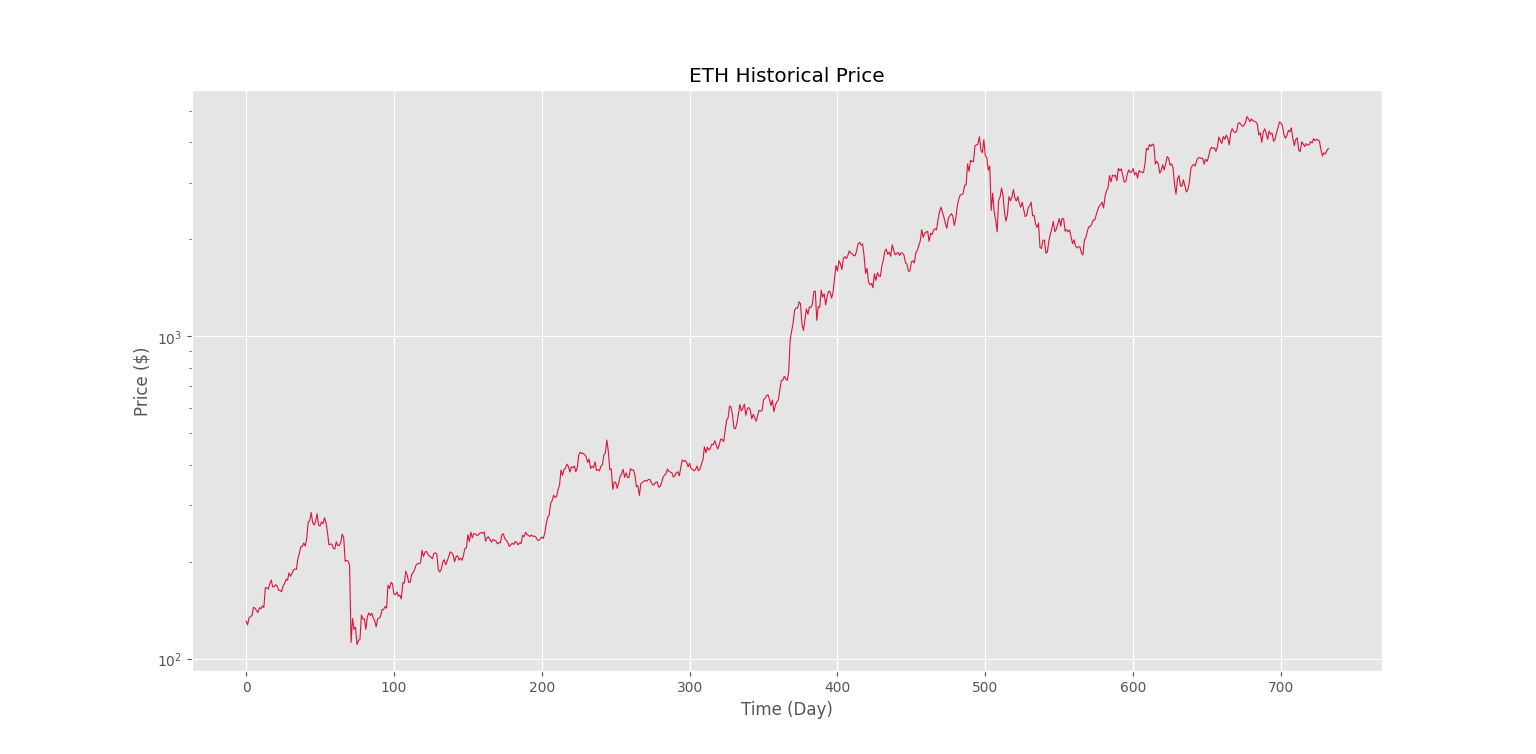
برای یادگیری برنامه‌نویسی با زبان پایتون، پیشنهاد می‌کنیم به مجموعه آموزش‌های مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه آموزش‌های برنامه نویسی پایتون (Python) — مقدماتی تا پیشرفته + اینجا کلیک کنید.

حال یک $$L$$ تعریف می‌کنیم سپس $$d$$ و سری زمانی جدید را محاسبه می‌کنیم:

L = 10
d = round((L - 1) / 2)

S = Closes[d:] + (Closes[d:] - Closes[:-d])

حال می‌توانیم سری زمانی جدید را در کنار نمودار اصلی قیمت رسم کنیم تا تفاوت آشکار شود:

T = np.arange(start=0, stop=Closes.size, step=1)

plt.semilogy(T, Closes, ls='-', lw=0.8, c='crimson', label='Close')
plt.semilogy(T[-S.size:], S, ls='-', lw=0.8, c='teal', label='S')
plt.title('ETH Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()

پس از اجرا، شکل زیر را خواهیم داشت.

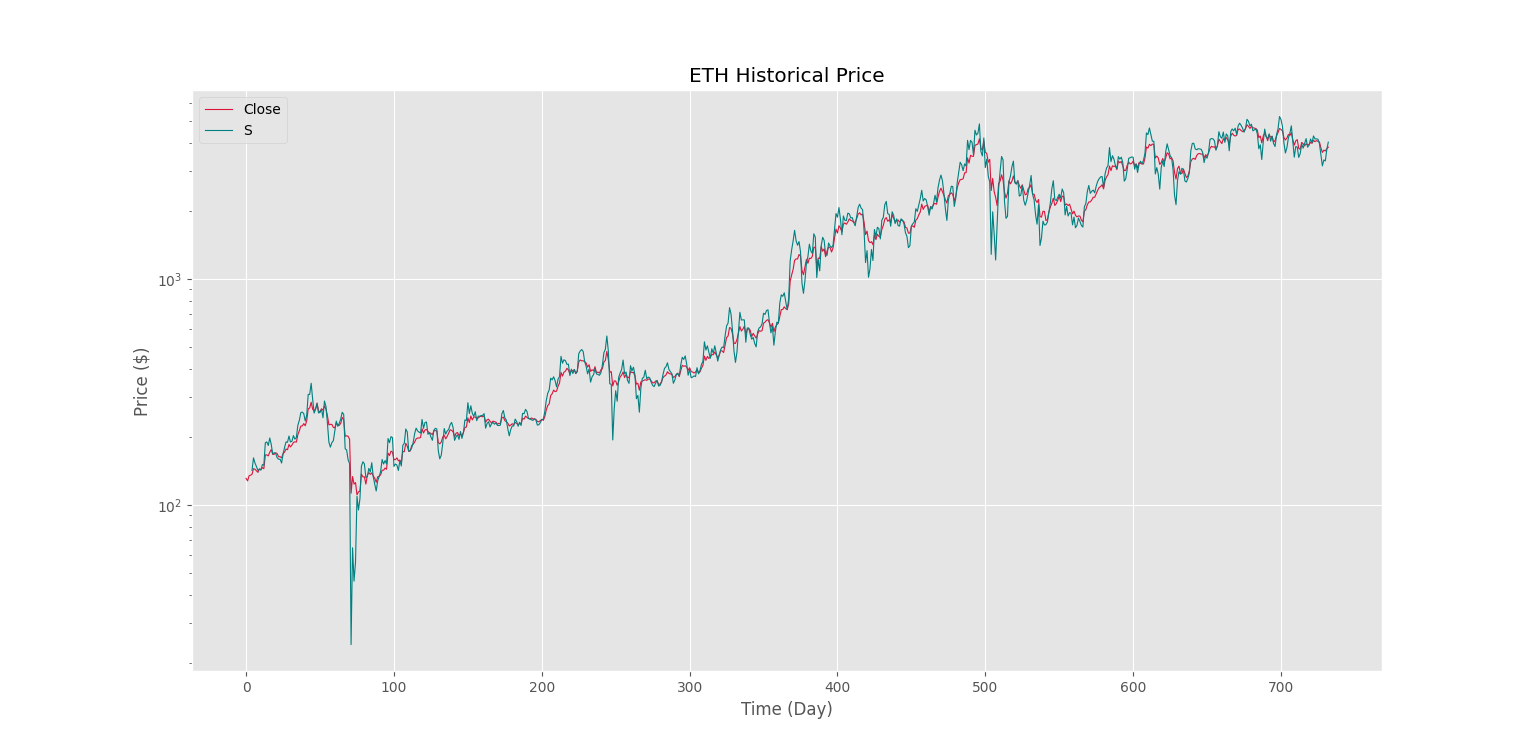
به این ترتیب، مشاهده می‌کنیم که سری زمانی دوم، حول سری زمانی اولی نوسان می‌کند و بخشی از تکانه (Momentum) موجود نیز در سری اضافه شده است. برای برخی نقاط، رفتار بسیار شدیدی رخ داده است. این مشکل از شیوه محاسبه سری زمانی دوم حاصل شده است و به شکل جمعی (Additive) است. با توجه به اینکه ذات بازارهای مالی به شکل ضربی (Multiplicative) است، می‌توان روش محاسبه سری را به شکل زیر تغییر داد:

$$ S_{t}=X_{t} timesleft(frac{X_{t}}{X_{t-d}}right) $$

برای اعمال این تغییر در کد، به شکل زیر عمل می‌کنیم:

S = np.multiply(Closes[d:], (Closes[d:] / Closes[:-d]))

پس از اجرای کد و رسم نمودار، به شکل زیر می‌رسیم.

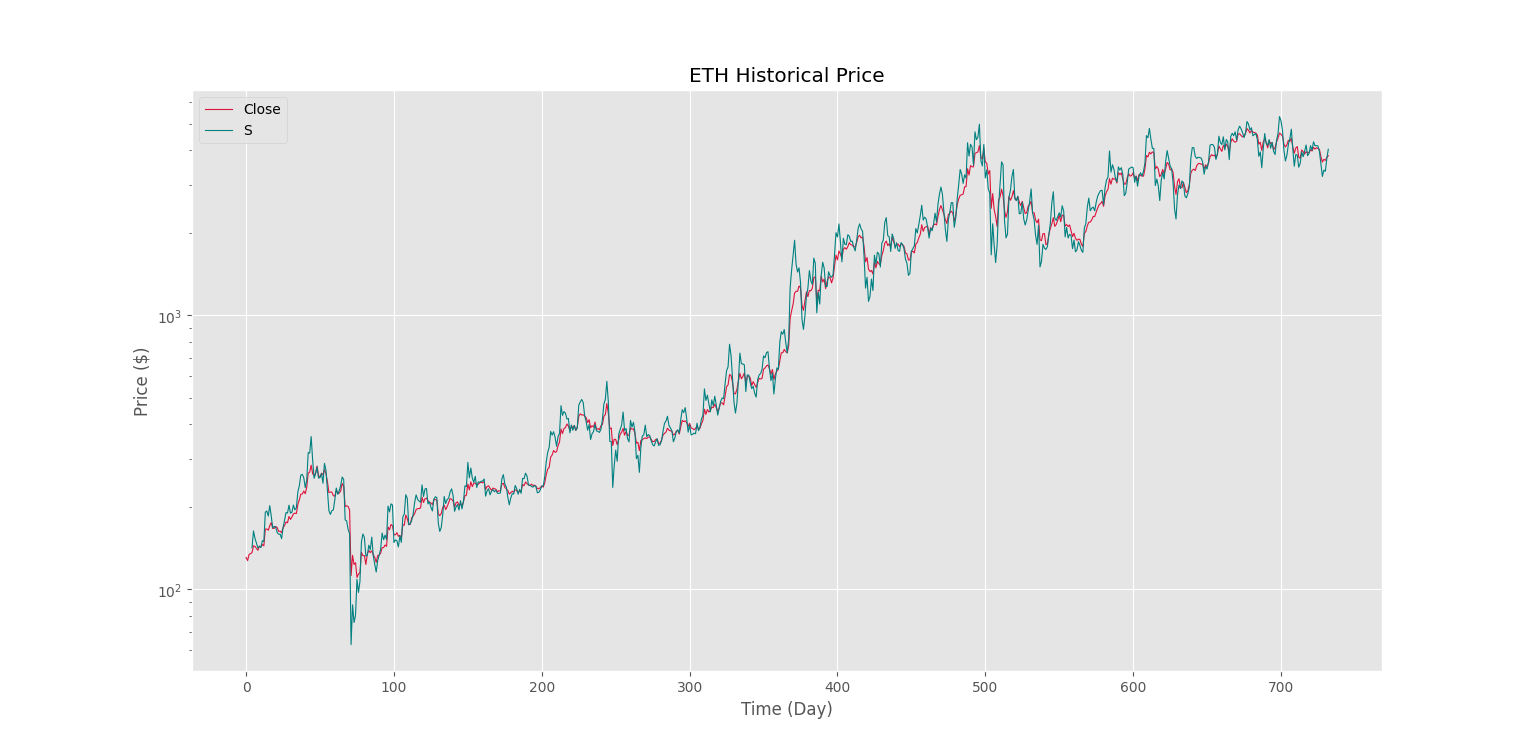
به این ترتیب، مشاهده می‌کنیم که رفتار سری دوم در این حالت بهتر است؛ به همین دلیل، در ادامه مطلب نیز از حالت ضربی استفاده خواهیم کرد.

حال می‌توانیم اندیکاتور مورد نظر را در قالب یک تابع پیاده‌سازی کنیم. این تابع در ورودی سری زمانی اصلی و طول پنجره میانگین‌گیری را خواهد گرفت:

def ZLEMA(S:np.ndarray, L:int):

حال میتوانیم $$d$$ و سری زمانی جدید را محاسبه کنیم:

def ZLEMA(S:np.ndarray, L:int):
    d = round((L - 1) / 2)
    S2 = np.multiply(S[d:], (S[d:] / S[:-d]))

حال میانگین متحرک نمایی را اعمال کرده و خروجی را برمی‌گردانیم:

def ZLEMA(S:np.ndarray, L:int):
    d = round((L - 1) / 2)
    S2 = np.multiply(S[d:], (S[d:] / S[:-d]))
    zlema = EMA(S2, L)
    return zlema

به این ترتیب، اندیکاتور کامل می‌شود. برای تابع مربوط به میانگین متحرک نمایی نیز از کد زیر استفاده می‌کنیم:

def EMA(S:np.ndarray, L:int):
    a = 2 / (L + 1)
    nD0 = S.size
    nD = nD0 - L + 1
    M = np.zeros(nD)
    M[0] = np.mean(S[:L])
    for i in range(1, nD):
        M[i] = a*S[i+L-1] + (1-a)*M[i-1]
    return M

استفاده از تابع

برای استفاده از اندیکاتور، به شکل زیر تابع را فراخوانی کرده و خروجی را دریافت می‌کنیم:

zlema = ZLEMA(Closes, 20)

حال نمودار قیمت را به همراه میانگین متحرک نمایی بدون تأخیر رسم می‌کنیم:

T = np.arange(start=0, stop=Closes.size, step=1)

plt.semilogy(T, Closes, ls='-', lw=0.8, c='crimson', label='Close')
plt.semilogy(T[-zlema.size:], zlema, ls='-', lw=0.8, c='teal', label='ZLEMA(20)')
plt.title('ETH Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()

که پس از اجرا، شکل زیر را خواهیم داشت.

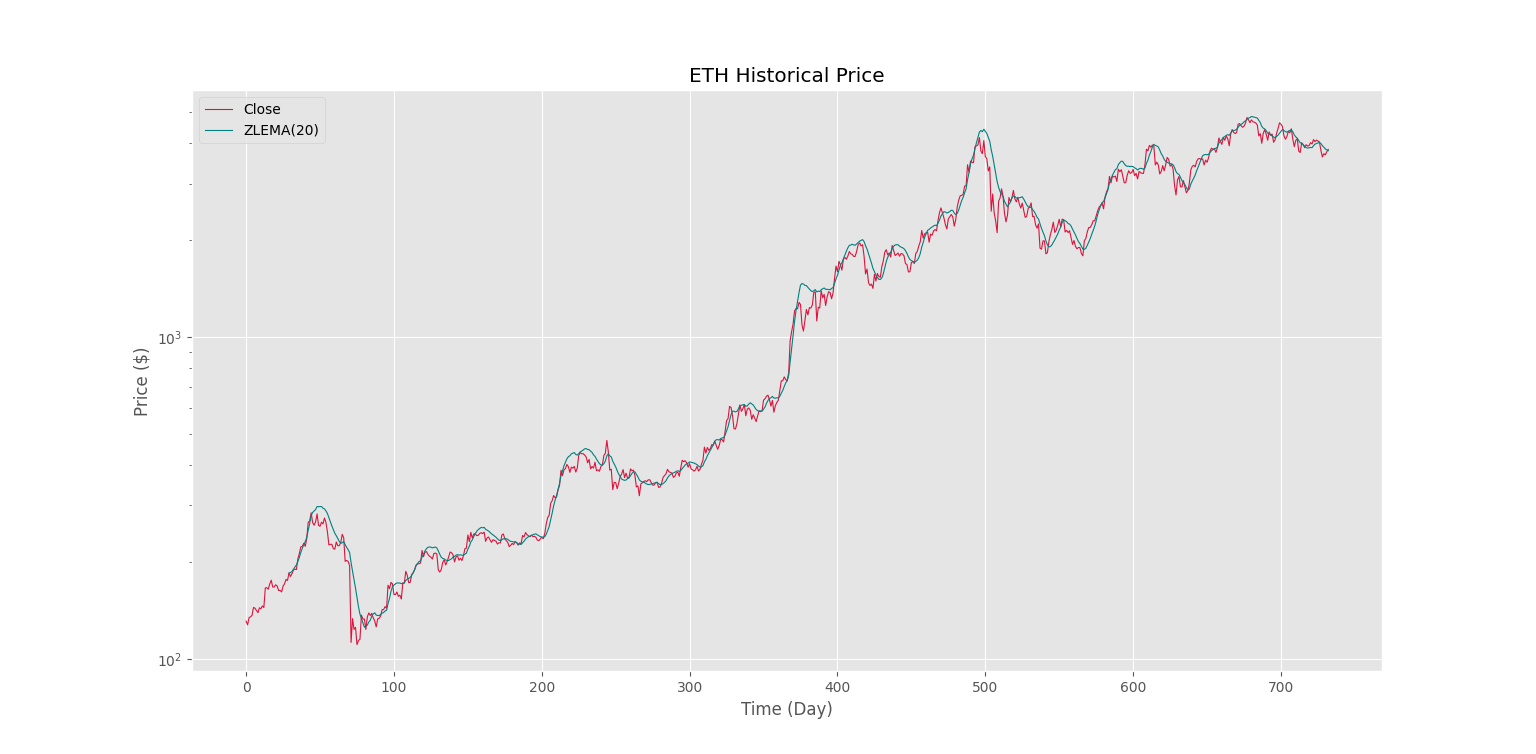
به این ترتیب، مشاهده می‌کنیم که در روند‌ها میانگین متحرک نمایی به خوبی همراه با قیمت حرکت می‌کند و به محض جاماندگی قیمت از میانگین متحرک، برگشت روند رخ می‌دهد.

اگر از حالت جمعی استفاده می‌کردیم، نمودار به شکل زیر می‌بود.

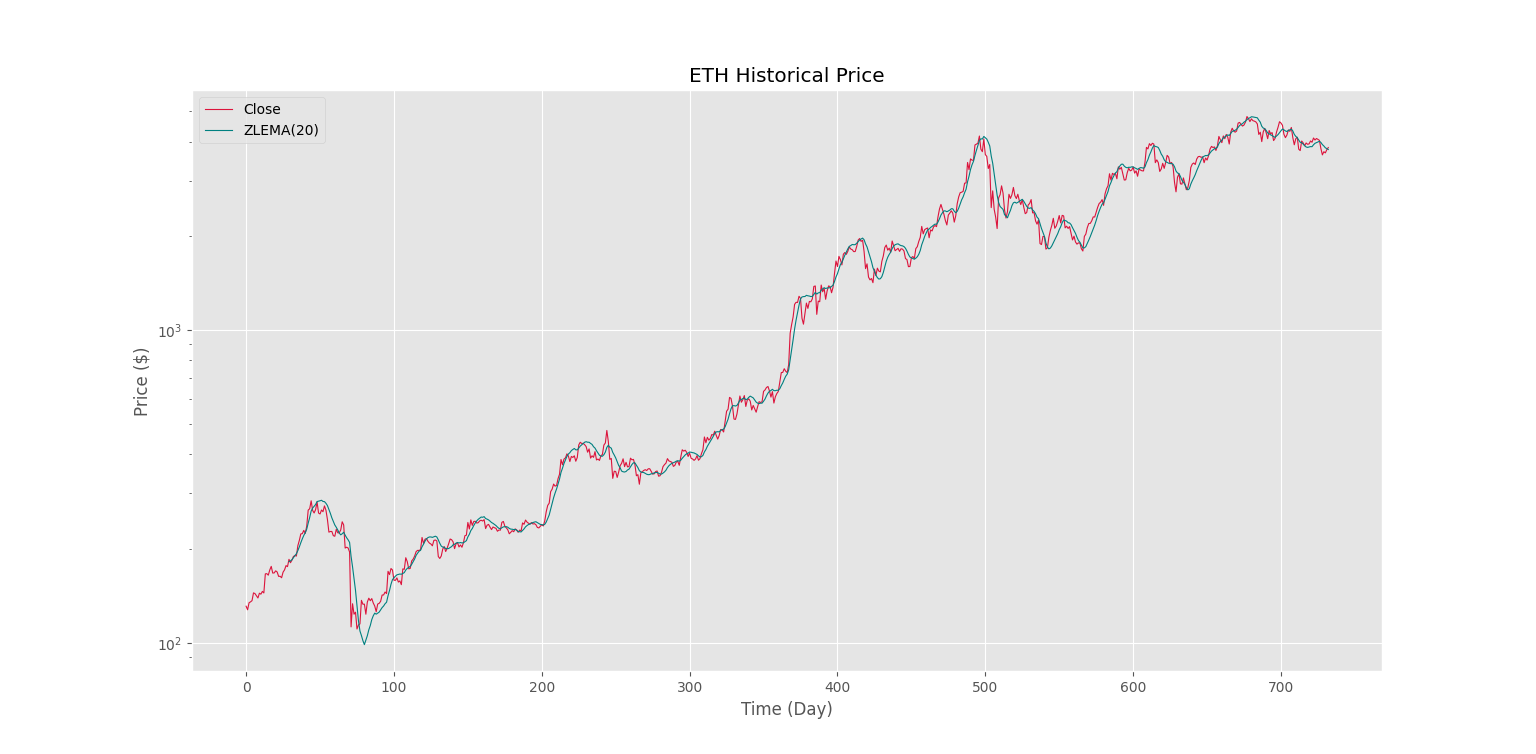
به این ترتیب، مشاهده می‌کنیم که در اغلب نقاط، تقریباً رفتار مشابهی وجود دارد، جز در نقاط برگشت روند. برای استفاده‌های بعدی، می‌توان هر دو حالت را در طول پنجره یکسان استفاده کرد و نتایج هرکدام را با یکدیگر مقایسه کرد.

برای مقایسه رفتار این اندیکاتور با میانگین متحرک ساده (Simple Moving Average | SMA) و میانگین متحرک نمایی، به شکل زیر کد مربوط به میانگین متحرک ساده را نیز وارد کد می‌کنیم:

def SMA(S:np.ndarray, L:int):
    nD0 = S.size
    nD = nD0 - L + 1
    sma = np.zeros(nD)
    for i in range(nD):
        sma[i] = np.mean(S[i:i + L])
    return sma

حال هر سه میانگین متحرک را با طول پنجره یکسان محاسبه می‌کنیم:

sma = SMA(Closes, 20)
ema = EMA(Closes, 20)
zlema = ZLEMA(Closes, 20)

سپس نمودار هر سه را به همراه قیمت رسم می‌کنیم:

plt.semilogy(T, Closes, ls='-', lw=0.8, c='crimson', label='Close')
plt.semilogy(T[-sma.size:], sma, ls='-', lw=0.8, c='teal', label='SMA(20)')
plt.semilogy(T[-ema.size:], ema, ls='-', lw=0.8, c='k', label='EMA(20)')
plt.semilogy(T[-zlema.size:], zlema, ls='-', lw=0.8, c='lima', label='ZLEMA(20)')
plt.title('ETH Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()

پس از اجرا شکل زیر را خواهیم داشت.

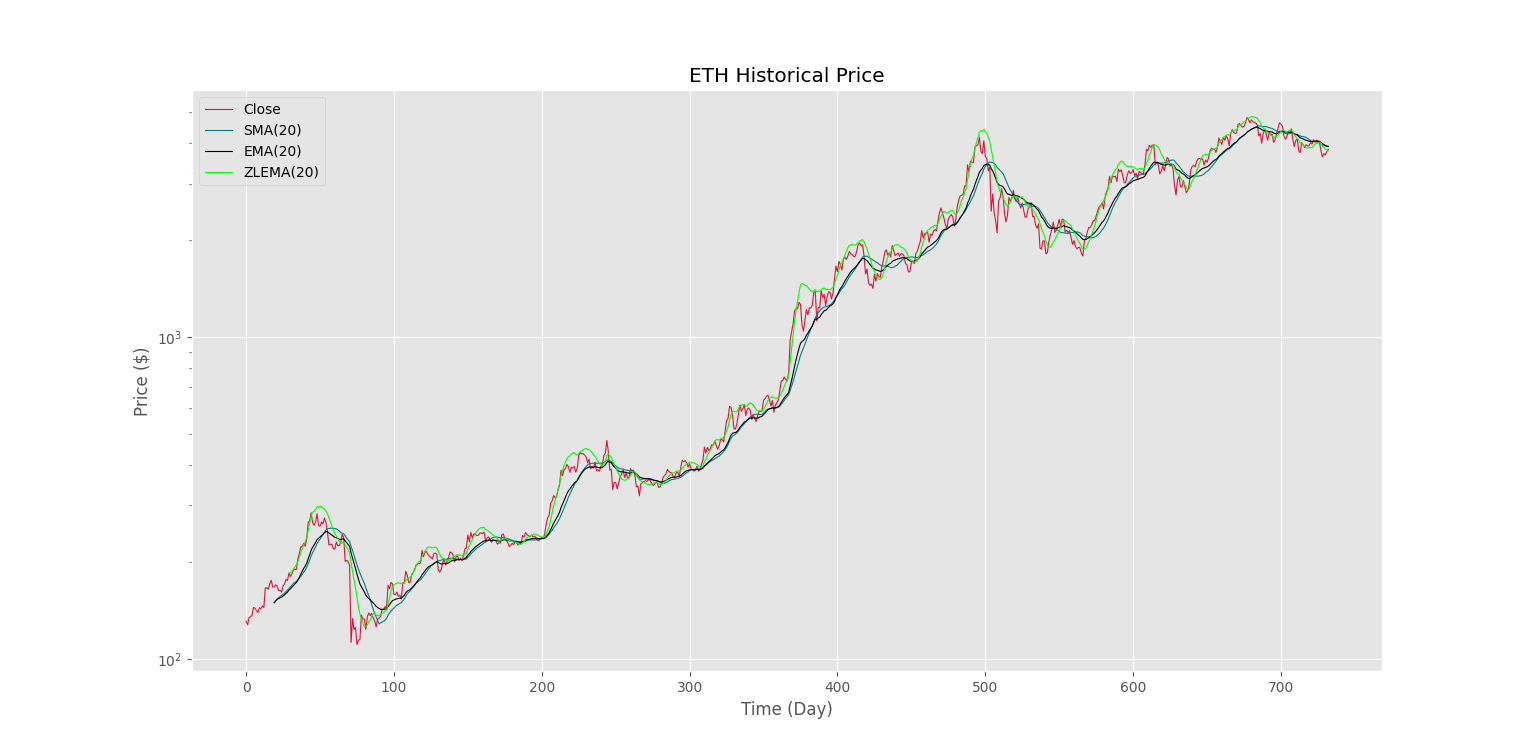
به این ترتیب، عملکرد فوق‌العاده این اندیکاتور مشخص می‌شود. توجه داشته باشید که در برخی نقاط، در حالی که میانگین متحرک ساده و میانگین متحرک نمایی، یک حمایت را نشان می‌دهند، ولی میانگین متحرک نمایی بدون تأخیر، یک مقاوت را نشان می‌دهد که قابل اعتماد است.

حال اگر اندازه پنجره را برای هر سه میانگین متحرک از ۲۰ روز به ۸۰ روز افزایش دهیم، نمودار زیر حاصل می‌شود.

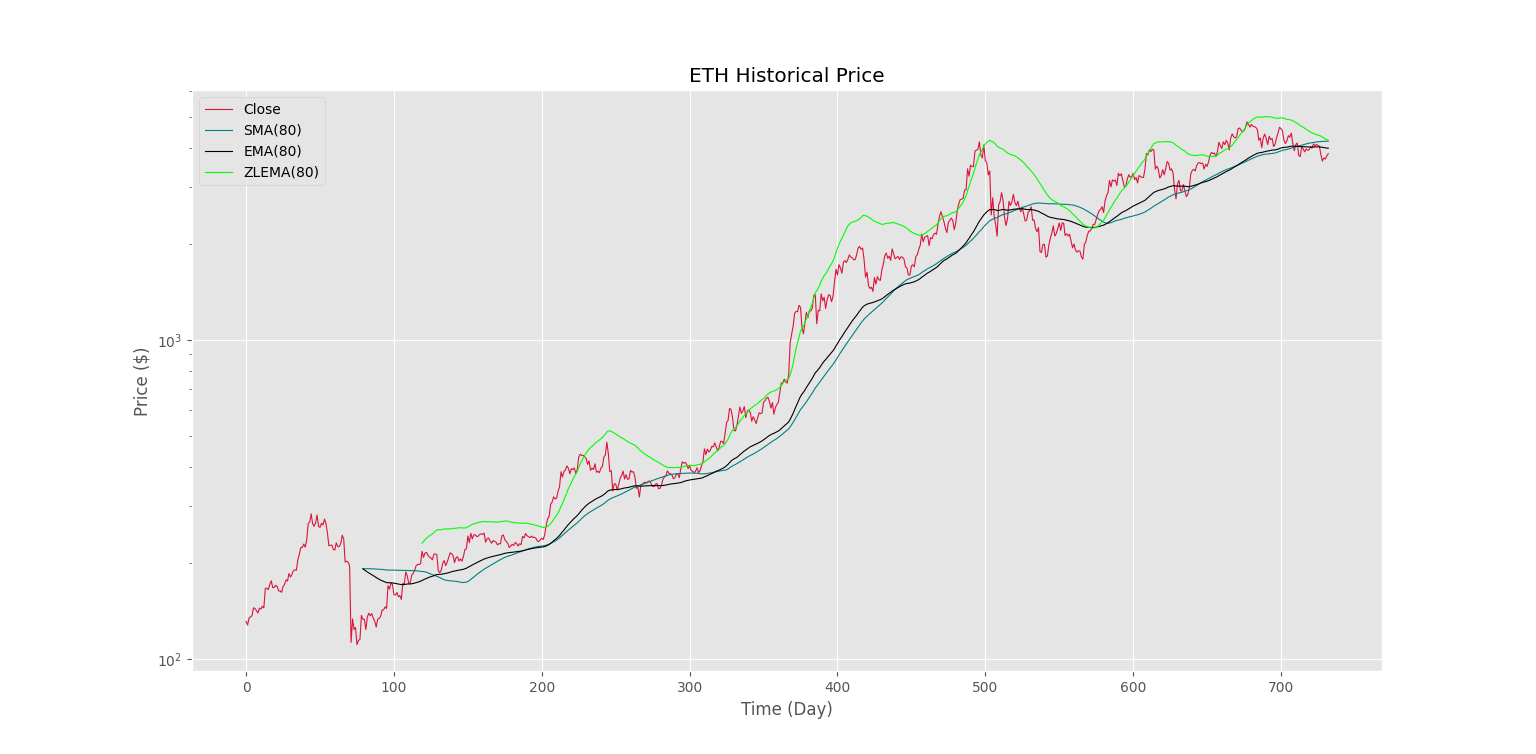
مشاهده می‌کنیم که در طول پنجره بیشتر نیز رفتار این اندیکاتور مناسب است. نکته مهم دیگر که باید به آن توجه کرد، تمایل این اندیکاتور برای خطی شدن در طول روندها است و در هنگام تغییر جهت قیمت، از حالت خطی خارج می‌شود.

فیلم آموزش میانگین متحرک – تحلیل تکنیکال در بورس و سرمایه گذاری در بازارهای مالی با Moving Average در تم آف

کلیک کنید

توجه داشته باشید که با افزایش طول پنجره، برخی رفتارهای نامتعادل از اندیکاتور بروز می‌کند که به دلیل افزوده شدن تغییرات $$d$$ روز گذشته به قیمت است. برای رفع این مشکل می‌توان تغییراتی در محاسبات $$d$$ انجام داد و رشد آن را محدود کرد.

جمع‌بندی

در این مطلب، میانگین متحرک نمایی بدون تأخیر را بررسی و پیاده‌سازی کردیم. برای مطالعه بیشتر در این زمینه، می‌توان موارد زیر را بررسی کرد:

1. چه تغییراتی می‌توان در محاسبه $$d$$ اعمال کرد؟
2. آیا می‌توان اصلاح انجام‌شده روی سری زمانی را روی میانگین متحرک نمایی انجام داد؟
3. اگر به جای میانگین متحرک نمایی، از میانگین متحرک ساده بر روی سری زمانی ثانویه استفاده، نتایج چه تغییری خواهد کرد؟
4. چه روش‌های دیگری برای کاهش تأخیر در میانگین متحرک‌ها وجود دارد؟