برنامه نویسی و طراحی سایت

پیاده سازی اندیکاتور مکدی MACD در پایتون — راهنمای گام به گام

  • ارسال شده توسط author-avatar
پیاده سازی اندیکاتور مکدی MACD در پایتون — راهنمای گام به گام
03 آبان

میانگین‌های متحرک (Moving Average یا MA) به‌تنهایی ابزارهایی ساده و بسیار کاربردی هستند که در اغلب ابزارهای «تحلیل تکنیکال» (Technical Analysis) ردپایی از آن‌ها دیده می‌شود. یکی از این ابزارها، اندیکاتور همگرایی-واگرایی میانگین متحرک (MACD یا Moving Average Convergence-Divergence) یا مکدی است. در این آموزش از «مجله تم آف»، به پیاده سازی اندیکاتور مکدی MACD در پایتون می‌پردازیم.

فهرست مطالب این نوشته
آشنایی با اندیکاتور مکدی (MACD)

دریافت و رسم مجموعه داده

پیاده‌سازی اندیکاتور MACD با استفاده از Numpy

پیاده‌سازی اندیکاتور MACD با استفاده از Pandas

محاسبه چندین MACD و رسم آن‌ها

جمع‌بندی

faradars mobile

آشنایی با اندیکاتور مکدی (MACD)

در این اندیکاتور ابتدا با تعیین $$L_1$$ و $$L_2$$ دو میانگین متحرک نمایی (Exponential Moving Average یا EMA) با طول پنجره متفاوت بر روی قیمت محاسبه می‌شود:

$$begin{aligned}
&E M A 1_{t}=E M A_{t}left(text {Close }, L_{1}right) \
&E M A 2_{t}=E M A_{t}left(text {Close }, L_{2}right)
end{aligned}$$

توجه داشته باشید که $$L_1$$ همواره باید کوچک‌تر از $$L_2$$ باشد. سپس اختلاف بین این دو میانگین متحرک به شکل زیر محاسبه می‌شود و مقدار حاصل MACD نامیده می‌شود:

$$M A C D_{t}=E M A 1_{t}-E M A 2_{t} $$

به این ترتیب، مقدار MACD فاصله و موقعیت این دو میانگین متحرک نسبت به هم را نشان خواهد داد. تا به اینجا ابزار ایجادشده می‌تواند کاربردی باشد، اما یک بخش جدید نیز به آن اضافه می‌شود تا سیگنال‌های بهتری تولید کند.

آموزش برنامه نویسی پایتون Python – مقدماتی
فیلم آموزش برنامه نویسی پایتون Python – مقدماتی در تم آف

کلیک کنید

در این مرحله با تعیین یک $$L_s$$ که طول میانگین متحرک سیگنال است، از خط MACD یک میانگین متحرک نمایی گرفته می‌شود:

$${Signal}_{t}=E M A_{t}left(M A C D, L_{s}right)$$

بنابراین، می‌توانیم حدس بزنیم که حرکت خط Signal کندتر از MACD خواهد بود. اختلاف این دو خط را نیز به عنوان معیار جدیدی به نام هیستوگرام (Histogram) نشان می‌دهیم:

$$ { Histogram }_{t}=M A C D_{t}- { Signal }_{t} $$

 به این ترتیب، در خروجی سه خط با نام‌های MACD و Signal و Histogram خواهیم داشت.

برای $$L_1$$ و $$L_2$$ و $$L_s$$ معمولاً، به‌ترتیب، از اعداد ۱۲ و ۲۶ و ۹ استفاده می‌شود که تنظیمات مشهوری بوده و نتایج خوبی را ایجاد می‌کند.

اندیکاتور MACD سیگنال‌های متنوعی می‌تواند ایجاد کند که هرکدام در شرایطی از اعتبار بالایی برخوردار هستند. برای آشنایی بیشتر با اندیکاتور MACD می‌توانید به مطلب «اندیکاتور MACD چیست؟ آموزش تصویری و به زبان ساده» مراجعه کنید.

آموزش پیاده سازی اندیکاتورهای تکنیکال با پایتون Python – بخش یکم
فیلم آموزش پیاده سازی اندیکاتورهای تکنیکال با پایتون Python – بخش یکم در تم آف

کلیک کنید

دریافت و رسم مجموعه داده

حال وارد محیط برنامه‌نویسی می‌شویم و کتابخانه‌های مورد نیاز را فراخوانی می‌کنیم: 

import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt

این 4 کتابخانه به ترتیب برای موارد زیر کاربرد دارند:

  1. کار با آرایه (Array) و محاسبات برداری (Vectorized Computation)
  2. کار با دیتافریم‌ها (Data Frame)
  3. دریافت داده از طریق API مربوط به Yahoo Finance
  4. رسم نمودار قیمت و اندیکاتور

حال تنظیمات زیر را برای نمودارها اعمال می‌کنیم تا ظاهر نمودارها مناسب باشد: 

plt.style.use('ggplot')

حال می‌توانیم مجموعه داده مربوط به شاخص بورس نزدک یا NASDAQ را دریافت کنیم. به این منظور از تابع yfinance.download استفاده می‌کنیم: 

DF = yf.download('^IXIC', start='2018-01-01', end='2022-01-01')

نماد مربوط به شاخص نزدک در Yahoo Finance به شکل IXIC^ است که برای یافتن آن‌ها می‌توان به سایت Yahoo Finance مراجعه کرد. حال برای بررسی مجموعه داده دریافتی، می‌توانیم از دو متد head و tail استفاده کنیم: 

print(DF.head())

print(DF.tail())

که در خروجی خواهیم داشت: 

                   Open         High          Low        Close    Adj Close      Volume
Date
2018-01-02  6937.649902  7006.910156  6924.080078  7006.899902  7006.899902  1914930000
2018-01-03  7017.069824  7069.149902  7016.700195  7065.529785  7065.529785  2166780000
2018-01-04  7089.500000  7098.049805  7072.379883  7077.910156  7077.910156  2098890000
2018-01-05  7105.740234  7137.040039  7097.080078  7136.560059  7136.560059  2020900000
2018-01-08  7135.379883  7161.350098  7124.089844  7157.390137  7157.390137  2051430000
                    Open          High           Low         Close     Adj Close      Volume
Date
2021-12-27  15696.830078  15871.400391  15696.830078  15871.259766  15871.259766  3730120000
2021-12-28  15895.200195  15901.469727  15757.070312  15781.719727  15781.719727  3623600000
2021-12-29  15794.919922  15821.809570  15679.849609  15766.219727  15766.219727  3694500000
2021-12-30  15758.980469  15868.089844  15729.160156  15741.559570  15741.559570  3732730000
2021-12-31  15722.910156  15777.429688  15643.940430  15644.969727  15644.969727  3379850000

به این ترتیب، می‌توان تا حدود زیادی از درستی مجموعه داده اطمینان یافت. حال می‌توانیم نمودار مربوط به ستون Close را نیز رسم و از روند شاخص مطلع شویم. برای این منظور، می‌توان هر دو روش زیر را در پیش گرفت و به نمودار رسید:

  1. رسم ستون مربوط به Close با استفاده از تاریخ
  2. رسم ستون مربوط به Close پس از تبدیل به آرایه با استفاده از شماره داده

برای مورد اول، می‌توانیم به شکل زیر عمل کنیم: 

plt.semilogy(DF['Close'], ls='-', lw=0.9, c='k')
plt.title('NASDAQ Composite')
plt.xlabel('Date')
plt.ylabel('Value')
plt.show()

در این شرایط مجموعه داده را به آرایه Numpy تبدیل نمی‌کنیم و مقادیر محور افقی نیز تاریخ روزها است. در خروجی نمودار زیر حاصل می‌شود.

مکدی در پایتون

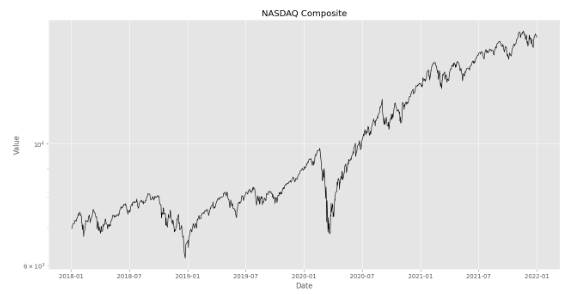
به این ترتیب، نمودار مورد نظر حاصل می‌شود. حال برای حالت دوم از رسم نمودار، ابتدا مقادیر ستون Close را به شکل آرایه Numpy دریافت می‌کنیم:

C = DF['Close'].to_numpy()

حال یک آرایه دیگر به‌عنوان شماره روزها ایجاد می‌کنیم. بدین منظور، تابع numpy.arange مناسب است: 

T = np.arange(start=1, stop=C.size + 1, step=1)

حال می‌توانیم رسم نمودار را دوباره تکرار کنیم: 

plt.semilogy(T, C, ls='-', lw=0.9, c='k')
plt.title('NASDAQ Composite')
plt.xlabel('Time (Day)')
plt.ylabel('Value')
plt.show()

در این حالت نیز نمودار به‌شکل زیر حاصل خواهد شد.

پیاده سازی اندیکاتور MACD

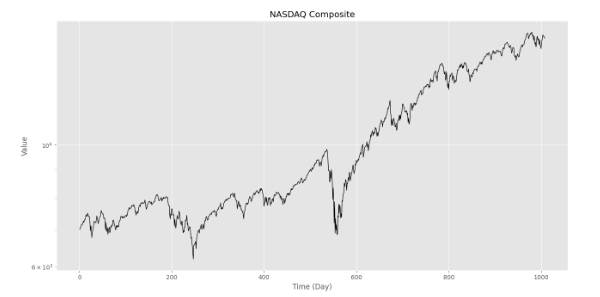
در نهایت، مشاهده می‌کنیم که مقادیر محور عمودی ثابت هستند، اما در محور افقی، به‌جای تاریخ شاهد شماره روزها هستیم.

بنابراین، روند کلی نماد و صحت مقادیر آن قابل مشاهده است. حال می‌توانیم اندیکاتور MACD را پیاده‌سازی کنیم.

برای یادگیری برنامه‌نویسی با زبان پایتون، پیشنهاد می‌کنیم به مجموعه آموزش‌های مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.

  • برای مشاهده مجموعه آموزش‌های برنامه نویسی پایتون (Python) — مقدماتی تا پیشرفته + اینجا کلیک کنید.

پیاده‌سازی اندیکاتور MACD با استفاده از Numpy

با توجه به اینکه در روند محاسبه اندیکاتور، از اندیکاتور EMA نیز استفاده می‌کنیم، باید آن را نیز وارد کد کنیم. تابع مربوط به EMA را به‌صورت زیر تعریف می‌کنیم: 

def EMA(S:np.ndarray, L:int, r:float=1):
    a = (1 + r) / (L + r)
    nD0 = S.size
    nD = nD0 - L + 1
    M = np.zeros(nD)
    M[0] = np.mean(S[:L])
    for i in range(1, nD):
        M[i] = a * S[i + L - 1] + (1 - a) * M[i - 1]
    return M

برای آشنایی با میانگین متحرک نمایی و روش پیاده‌سازی آن می‌توانید به مطلب «پیاده سازی میانگین متحرک نمایی در پایتون – راهنمای گام به گام» مراجعه کنید.

حال می‌توانیم یک تابع برای MACD ایجاد کنیم که در ورودی آرایه مربوط به Closeها، و مقادیر $$L_1$$ و $$L_2$$ و $$L_s$$  را دریافت کند: 

def MACD(C:np.ndarray, L1:int, L2:int, Ls:int):

حال در اولین مرحله، میانگین‌های متحرک نمایی را محاسبه می‌کنیم: 

def MACD(C:np.ndarray, L1:int, L2:int, Ls:int):
    ema1 = EMA(C, L1)
    ema2 = EMA(C, L2)

با توجه به اینکه برای محاسبه خط MACD نیاز داریم تا اختلاف بین این دو مقدار را محاسبه کنیم، باید طول دو آرایه ema1 و ema2 برابر باشد که نیست. برای برقراری این شرط، به‌شکل زیر تعدادی از اعضای ابتدای ema1 را حذف می‌کنیم تا هر دو هم‌اندازه شوند: 

def MACD(C:np.ndarray, L1:int, L2:int, Ls:int):
    ema1 = EMA(C, L1)
    ema2 = EMA(C, L2)
    ema1 = ema1[-ema2.size:]

حال می‌توانیم خط MACD را محاسبه کنیم: 

def MACD(C:np.ndarray, L1:int, L2:int, Ls:int):
    ema1 = EMA(C, L1)
    ema2 = EMA(C, L2)
    ema1 = ema1[-ema2.size:]
    macd = ema1 - ema2

در این مرحله، باید با اعمال EMA روی خط MACD، خط Signal را به‌دست آوریم: 

def MACD(C:np.ndarray, L1:int, L2:int, Ls:int):
    ema1 = EMA(C, L1)
    ema2 = EMA(C, L2)
    ema1 = ema1[-ema2.size:]
    macd = ema1 - ema2
    signal = EMA(macd, Ls)

به این ترتیب، این دو خط حاصل می‌شوند. با توجه به اینکه طول دو آرایه macd و signal با یکدیگر برابر نیست، باید بار دیگر چند عضو ابتدای macd را حذف کنیم تا خط Histogram قابل محاسبه باشد: 

def MACD(C:np.ndarray, L1:int, L2:int, Ls:int):
    ema1 = EMA(C, L1)
    ema2 = EMA(C, L2)
    ema1 = ema1[-ema2.size:]
    macd = ema1 - ema2
    signal = EMA(macd, Ls)
    macd = macd[-signal.size:]

حال محاسبه آرایه histogram امکان‌پذیر خواهد بود: 

def MACD(C:np.ndarray, L1:int, L2:int, Ls:int):
    ema1 = EMA(C, L1)
    ema2 = EMA(C, L2)
    ema1 = ema1[-ema2.size:]
    macd = ema1 - ema2
    signal = EMA(macd, Ls)
    macd = macd[-signal.size:]
    histogram = macd - signal

در انتهای تابع نیز موارد مورد نیاز را برمی‌گردانیم: 

def MACD(C:np.ndarray, L1:int, L2:int, Ls:int):
    ema1 = EMA(C, L1)
    ema2 = EMA(C, L2)
    ema1 = ema1[-ema2.size:]
    macd = ema1 - ema2
    signal = EMA(macd, Ls)
    macd = macd[-signal.size:]
    histogram = macd - signal
    return ema1, ema2, macd, signal, histogram

در نتیجه، این تابع کامل خواهد بود. برای استفاده از تابع، به‌شکل زیر آن را فراخوانی می‌کنیم: 

ema1, ema2, macd, signal, histogram = MACD(C, 12, 26, 9)

حال می‌توانیم با استفاده از matplotlib.pyplot.subplot دو نمودار مربوط به مقدار شاخص و اندیکاتور را در زیر هم رسم کنیم: 

plt.subplot(3, 1, (1, 2))
plt.semilogy(T, C, ls='-', lw=0.8, c='k', label='Close')
plt.semilogy(T[-ema1.size:], ema1, ls='-', lw=0.9, c='teal', label='EMA 1')
plt.semilogy(T[-ema2.size:], ema2, ls='-', lw=1.0, c='crimson', label='EMA 2')
plt.title('NASDAQ Composite')
plt.ylabel('Value')
plt.xlim(left=0, right=C.size + 1)
plt.tight_layout()
plt.legend()

plt.subplot(3, 1, 3)
plt.plot(T[-macd.size:], macd, ls='-', lw=0.8, c='k', label='MACD Line')
plt.plot(T[-signal.size:], signal, ls='-', lw=0.8, c='crimson', label='Signal Line')
plt.bar(T[-signal.size:], histogram, color='grey', label='Histogram')
plt.title('Moving Average Convergence Divergence (MACD)')
plt.xlabel('Time (Day)')
plt.ylabel('Value')
plt.xlim(left=0, right=C.size + 1)
plt.tight_layout()
plt.legend()

plt.show()

به این ترتیب، صفحه به سه سطر و یک ستون تقسیم خواهد شد و دو بخش بالایی برای رسم مقدار شاخص و میانگین‌های متحرک اختصاص خواهد یافت. یک بخش پایینی نیز برای رسم سه خط اندیکاتور استفاده خواهد شد. پس از اجرای این بخش از کد، نمودار زیر را خواهیم داشت.

اندیکاتور مکدی در python

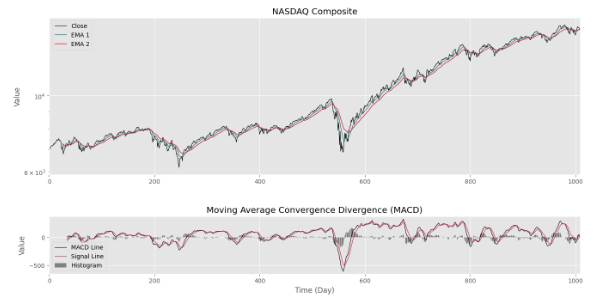
بنابراین، مشاهده می‌کنیم که تمامی موارد مورد نیاز رسم می‌شود. با توجه به اینکه نمودار هیستوگرام به شکل یک رنگ رسم شده است، ممکن است مناسب نباشد. از طرفی بین ستون‌ها نیز فاصله افتاده است. برای رفع این مشکل، کد را به‌شکل زیر تغییر می‌دهیم:

plt.subplot(3, 1, (1, 2))
plt.semilogy(T, C, ls='-', lw=0.9, c='k', label='Close')
plt.semilogy(T[-ema1.size:], ema1, ls='-', lw=0.9, c='teal', label='EMA 1')
plt.semilogy(T[-ema2.size:], ema2, ls='-', lw=1.0, c='crimson', label='EMA 2')
plt.title('NASDAQ Composite')
plt.ylabel('Value')
plt.xlim(left=0, right=C.size + 1)
plt.tight_layout()
plt.legend()

plt.subplot(3, 1, 3)
plt.plot(T[-macd.size:], macd, ls='-', lw=0.8, c='k', label='MACD Line')
plt.plot(T[-signal.size:], signal, ls='-', lw=0.8, c='crimson', label='Signal Line')
plt.bar(T[-signal.size:][histogram >= 0], histogram[histogram >= 0], color='b', width=1, label='Positive Histogram')
plt.bar(T[-signal.size:][histogram

برای جدا کردن مقادیر مثبت و منفی هیستوگرام، از maskهای موجود در کتابخانه Numpy استفاده می‌کنیم. مشکل جدایی ستون‌ها از هم نیز با تعیین width=1 قابل رفع است. حال اگر رسم نمودار را تکرار کنیم، شکل زیر را خواهیم داشت.

اندیکاتور مکدی در پایتون

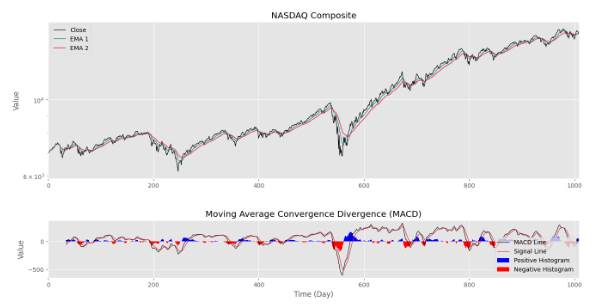
به این ترتیب، مصورسازی نمودار بهبود می‌یابد و اطلاعات به نحو بهتری منتقل می‌شود.

نکته مهم دیگری که در رابطه با این اندیکاتور وجود دارد، شیوه نگرش به اختلاف دو میانگین متحرک است. به دلیل اینکه خط MACD از اختلاف دو میانگین متحرک حاصل می‌شود، دارای روند خواهد بود و شدت نوسان آن وابسته به مقیاس قیمت خواهد بود. این اتفاق می‌تواند باعث ضعیف یا قوی شدن برخی سیگنال‌ها شود که مناسب نیست. برای رفع این مشکل، می‌توان محاسبه MACD را به‌شکل زیر انجام داد:

$$ M A C D_{t} =frac{E M A 1_{t}-E M A 2_{t}}{E M A 2_{t}}=frac{E M A 1_{t}}{E M A 2_{t}}-1 $$

بنابراین، مقیاس قیمت در مقدار MACD بی‌تأثیر خواهد بود. می‌توان از لگاریتم نسبت دو میانگین متحرک نیز استفاده کرد که رفتار بهتری دارد:

$$ M A C D_{t} =log left(frac{E M A 1_{t}}{E M A 2_{t}}right)
$$

حال حالت دوم را می‌توانیم در اندیکاتور اعمال کنیم که خواهیم داشت: 

def MACD(C:np.ndarray, L1:int, L2:int, Ls:int):
    ema1 = EMA(C, L1)
    ema2 = EMA(C, L2)
    ema1 = ema1[-ema2.size:]
    macd = np.log(ema1 / ema2)
    signal = EMA(macd, Ls)
    macd = macd[-signal.size:]
    histogram = macd - signal
    return ema1, ema2, macd, signal, histogram

در این شرایط، اگر نمودار را تکرار کنیم، شکل زیر را خواهیم داشت.

اندیکاتور مکدی

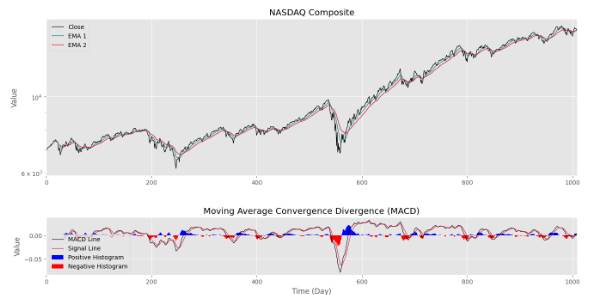
به این ترتیب، مشاهده می‌کنیم که تغییرات اندکی در ظاهر اندیکاتور مشاهده می‌شود. توجه داشته باشید که نتایج حاصل از این حالت، قابل تعمیم به سایر نمادهای نیز هست. از طرفی حذف روند از اندیکاتورها، در اغلب شرایط به نفع ما است.

آموزش اندیکاتورهای تحلیل روند برای تحلیل تکنیکال در بورس و بازارهای مالی
فیلم آموزش اندیکاتورهای تحلیل روند برای تحلیل تکنیکال در بورس و بازارهای مالی در تم آف

کلیک کنید

پیاده‌سازی اندیکاتور MACD با استفاده از Pandas

حال می‌توانیم به پیاده‌سازی اندیکاتور MACD با استفاده از امکانات کتابخانه Pandas بپردازیم. در این حالت نیز یک تابع ایجاد می‌کنیم و در ورودی دیتافریم را به همراه سه عدد $$L_1$$ و $$L_2$$ و $$L_s$$ دریافت می‌کنیم: 

def MACD(DF:pd.core.frame.DataFrame, L1:int, L2:int, Ls:int):

حال باید میانگین‌های متحرک نمایی را محاسبه کنیم. به این منظور، می‌توانیم از متد ewm استفاده کنیم و روی آن عمل میانگین‌‌گیری را انجام دهیم: 

def MACD(DF:pd.core.frame.DataFrame, L1:int, L2:int, Ls:int):
    DF['EMA1'] = DF['Close'].ewm(span=L1).mean()
    DF['EMA2'] = DF['Close'].ewm(span=L2).mean()

به این ترتیب، دو ستون جدید ایجاد شده و مقادیر میانگین‌های متحرک را در خود ذخیره خواهند کرد. در گام بعدی، اختلاف این دو ستون را محاسبه و به‌عنوان ستون MACD اضافه می‌کنیم: 

def MACD(DF:pd.core.frame.DataFrame, L1:int, L2:int, Ls:int):
    DF['EMA1'] = DF['Close'].ewm(span=L1).mean()
    DF['EMA2'] = DF['Close'].ewm(span=L2).mean()
    DF['MACD'] = DF['EMA1'] - DF['EMA2']

حال ستون Signal نیز با استفاده از ewm قابل محاسبه خواهد بود: 

def MACD(DF:pd.core.frame.DataFrame, L1:int, L2:int, Ls:int):
    DF['EMA1'] = DF['Close'].ewm(span=L1).mean()
    DF['EMA2'] = DF['Close'].ewm(span=L2).mean()
    DF['MACD'] = DF['EMA1'] - DF['EMA2']
    DF['Signal'] = DF['MACD'].ewm(span=Ls).mean()

برای محاسبه خط Histogram نیز تفاضل دو خط قبلی را محاسبه می‌کنیم: 

def MACD(DF:pd.core.frame.DataFrame, L1:int, L2:int, Ls:int):
    DF['EMA1'] = DF['Close'].ewm(span=L1).mean()
    DF['EMA2'] = DF['Close'].ewm(span=L2).mean()
    DF['MACD'] = DF['EMA1'] - DF['EMA2']
    DF['Signal'] = DF['MACD'].ewm(span=Ls).mean()
    DF['Histogram'] = DF['MACD'] - DF['Signal']

به این ترتیب، تمامی اجزا محاسبه می‌شود. نکته مهمی که در رابطه با این تابع وجود دارد، احتمال محاسبه چندین باره اندیکاتور است. برای مثال، ممکن است با چندین تنظیمات مختلف اندیکاتور محاسبه شود. در این شرایط، نتایج هر بار اجرا روی نتایج اجرای قبلی نوشته و مشکلاتی ایجاد خواهد شد. برای رفع این مشکل نام ستون‌ها را بر اساس پارامترهای ورودی تعیین می‌کنیم: 

def MACD(DF:pd.core.frame.DataFrame, L1:int, L2:int, Ls:int):
    DF[f'EMA({L1})'] = DF['Close'].ewm(span=L1).mean()
    DF[f'EMA({L2})'] = DF['Close'].ewm(span=L2).mean()
    DF[f'MACD({L1}, {L2})'] = DF[f'EMA({L1})'] - DF[f'EMA({L2})']
    DF[f'Signal({L1}, {L2}, {Ls})'] = DF[f'MACD({L1}, {L2})'].ewm(span=Ls).mean()
    DF[f'Histogram({L1}, {L2}, {Ls})'] = DF[f'MACD({L1}, {L2})'] - DF[f'Signal({L1}, {L2}, {Ls})']

در نتیجه، نام هر ستون برگرفته از پارامترهای مورد استفاده در محاسبه آن خواهد بود. توجه داشته باشید که خط MACD تنها از مقادیر $$L_1$$ و $$L_2$$ تأثیر می‌پذیرد و ذکر مقدار $$L_s$$ در نام آن بیهوده خواهد بود. حال تابع را فراخوانی می‌کنیم: 

MACD(DF, 12, 26, 9)

پس از اجرای کد فوق، می‌توانیم ستون‌های موجود در دیتافریم را با کد زیر بررسی کنیم: 

print(DF.columns.to_list())

که خواهیم داشت: 

['Open', 'High', 'Low', 'Close', 'Adj Close', 'Volume', 'EMA(12)', 'EMA(26)', 'MACD(12, 26)', 'Signal(12, 26, 9)', 'Histogram(12, 26, 9)']

به این ترتیب، مشاهده می‌کنیم که تمامی موارد مورد نیاز به درستی اضافه شده‌اند. حال برای رسم نمودار از کد زیر استفاده می‌کنیم: 

plt.subplot(3, 1, (1, 2))
plt.semilogy(DF['Close'], ls='-', lw=0.9, c='k', label='Close')
plt.semilogy(DF['EMA(12)'], ls='-', lw=0.9, c='teal', label='EMA(12)')
plt.semilogy(DF['EMA(26)'], ls='-', lw=1.0, c='crimson', label='EMA(26)')
plt.title('NASDAQ Composite')
plt.ylabel('Value')
plt.tight_layout()
plt.legend()

plt.subplot(3, 1, 3)
plt.plot(DF['MACD(12, 26)'], ls='-', lw=0.8, c='k', label='MACD(12, 26)')
plt.plot(DF['Signal(12, 26, 9)'], ls='-', lw=0.8, c='crimson', label='Signal(12, 26, 9)')
plt.bar(DF.index[DF['Histogram(12, 26, 9)'] >= 0], DF['Histogram(12, 26, 9)'][DF['Histogram(12, 26, 9)'] >= 0], color='b', width=1, label='+Histogram(12, 26, 9)')
plt.bar(DF.index[DF['Histogram(12, 26, 9)']

توجه داشته باشید که به‌دلیل استفاده از ستون‌های دیتافریم برای رسم نمودار، نیازی به تعریف آرایه زمان نیست و به‌صورت خودکار از Index دیتافریم استفاده می‌شود. نکته مهم دیگری که وجود دارد، روش تشخیص روزهای با هیستوگرام مثبت و منفی است. می‌توان با استفاده از Mask این کد را به‌شکل زیر ساده‌تر کرد: 

plt.subplot(3, 1, (1, 2))
plt.semilogy(DF['Close'], ls='-', lw=0.9, c='k', label='Close')
plt.semilogy(DF['EMA(12)'], ls='-', lw=0.9, c='teal', label='EMA(12)')
plt.semilogy(DF['EMA(26)'], ls='-', lw=1.0, c='crimson', label='EMA(26)')
plt.title('NASDAQ Composite')
plt.ylabel('Value')
plt.tight_layout()
plt.legend()

plt.subplot(3, 1, 3)
m = DF['Histogram(12, 26, 9)'] >= 0
plt.plot(DF['MACD(12, 26)'], ls='-', lw=0.8, c='k', label='MACD(12, 26)')
plt.plot(DF['Signal(12, 26, 9)'], ls='-', lw=0.8, c='crimson', label='Signal(12, 26, 9)')
plt.bar(DF.index[m], DF['Histogram(12, 26, 9)'][m], color='b', width=1, label='+Histogram(12, 26, 9)')
plt.bar(DF.index[~m], DF['Histogram(12, 26, 9)'][~m], color='r', width=1, label='-Histogram(12, 26, 9)')
plt.title('Moving Average Convergence Divergence (MACD)')
plt.xlabel('Time (Day)')
plt.ylabel('Value')
plt.tight_layout()
plt.legend()

plt.show()

به این ترتیب، کد هم بهینه شده و هم ساده‌تر می‌شود. پس از اجرای کد، تصویر زیر را خواهیم داشت.

نمودار مکدی

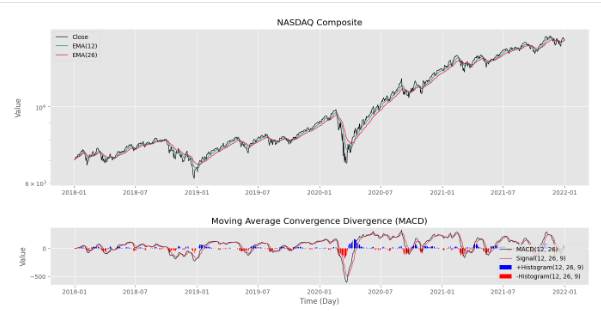
به این ترتیب، نمودار مورد نظر حاصل می‌شود. توجه داشته باشید که برای روزهای تعطیل، مقداری وجود ندارد و نمودار خالی خواهد بود.

برای حذف روند، می‌توان تابع را به‌صورت زیر تغییر داد: 

def MACD(DF:pd.core.frame.DataFrame, L1:int, L2:int, Ls:int):
    DF[f'EMA({L1})'] = DF['Close'].ewm(span=L1).mean()
    DF[f'EMA({L2})'] = DF['Close'].ewm(span=L2).mean()
    DF[f'MACD({L1}, {L2})'] = np.log(DF[f'EMA({L1})'] / DF[f'EMA({L2})'])
    DF[f'Signal({L1}, {L2}, {Ls})'] = DF[f'MACD({L1}, {L2})'].ewm(span=Ls).mean()
    DF[f'Histogram({L1}, {L2}, {Ls})'] = DF[f'MACD({L1}, {L2})'] - DF[f'Signal({L1}, {L2}, {Ls})']

در نتیجه، از نسبت لگاریتم دو میانگین متحرک استفاده خواهد شد.

آموزش کتابخانه های NumPy و Matplotlib در پایتون
فیلم آموزش کتابخانه های NumPy و Matplotlib در پایتون در تم آف

کلیک کنید

محاسبه چندین MACD و رسم آن‌ها

با توجه به اینکه ممکن است برای تحلیل وضعیت نمادها یا انجام معاملات الگوریتمی نیاز به چندین MACD با تنظیمات مختلف داشته باشیم، می‌توانیم به‌صورت زیر چندین MACD را محاسبه کنیم: 

MACD(DF, 12, 26, 9)
MACD(DF, 18, 39, 14)

پس از اجرای کد فوق، ستون‌های زیر در دیتافریم موجود خواهد بود: 

['Open', 'High', 'Low', 'Close', 'Adj Close', 'Volume', 'EMA(12)', 'EMA(26)', 'MACD(12, 26)', 'Signal(12, 26, 9)', 'Histogram(12, 26, 9)', 'EMA(18)', 'EMA(39)', 'MACD(18, 39)', 'Signal(18, 39, 14)', 'Histogram(18, 39, 14)']

بنابراین، مشاهده می‌کنیم که 10 ستون اخیر، حاصل فراخوانی توابع MACD با دو تنظیمات متفاوت هستند. حال می‌توانیم برای مقایسه، دو خط Histogram را در کنار هم رسم کنیم. به این منظور، می‌توان کد زیر را استفاده کرد: 

plt.subplot(3, 1, (1, 2))
plt.semilogy(DF['Close'], ls='-', lw=0.9, c='k')
plt.title('NASDAQ Composite')
plt.ylabel('Value')
plt.tight_layout()

plt.subplot(3, 1, 3)
plt.plot(DF['Histogram(12, 26, 9)'], ls='-', lw=0.8, c='crimson', label='Histogram(12, 26, 9)')
plt.plot(DF['Histogram(18, 39, 14)'], ls='-', lw=0.8, c='teal', label='Histogram(18, 39, 14)')
plt.title('Moving Average Convergence Divergence (MACD)')
plt.xlabel('Time (Day)')
plt.ylabel('Value')
plt.tight_layout()
plt.legend()

plt.show()

پس از اجرای کد فوق، شکل زیر را خواهیم داشت.

پیاده سازی MACD در پایتون

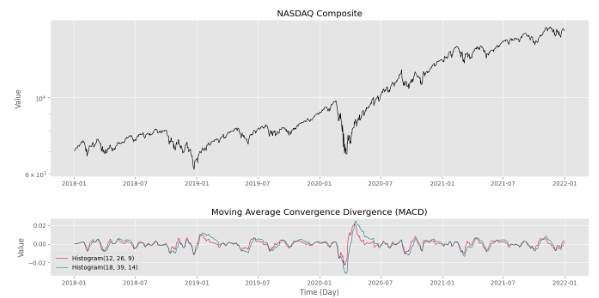
در نهایت، مشاهده می‌کنیم که بین دو خط همبستگی بالایی وجود دارد، اما تفاوت‌هایی نشان داده می‌شود که می‌تواند برای مقاصد مختلف استفاده شود. به این ترتیب، می‌توانیم با طراحی درست تابع، از آن به‌دفعات مختلف استفاده کنیم.

آموزش پیاده سازی گام به گام شبکه های عصبی در پایتون
فیلم آموزش پیاده سازی گام به گام شبکه های عصبی در پایتون در تم آف

کلیک کنید

جمع‌بندی

در این آموزش، پیاده‌سازی اندیکاتور MACD را انجام دادیم. برای مطالعه بیشتر، می‌توان موارد زیر را بررسی کرد:

  1. چرا تنظیمات 12 و 26 و 9 عملکرد خوبی دارد؟
  2. چرا در اندیکاتور MACD از SMA استفاده نمی‌شود؟
  3. بررسی کنید از این اندیکاتور چه سیگنال‌های می‌شود گرفت؟
  4. در MACD برخورد دو میانگین متحرک با یکدیگر چگونه نشان داده می‌شود؟
  5. با مراجعه به مطالب نوشته‌شده در رابطه با ربات‌های معامله‌گر، یک ربات براساس اندیکاتور MACD ایجاد کرده و آن را آموزش دهید.
  6. خط Signal، چه ارتباطی با سطح بین نمودار دو میانگین متحرک دارد؟
  7. در بخشی از کد، از Maskها استفاده شد. در مورد Maskها تحقیق کنید و کار عملگر Tild یا ~ را برای آن بیابید.
جدیدتر بازی Senua’s Saga: Hellblade 2 احتمالا به‌صورت کامل قابل بازی است
بازگشت به لیست
قدیمی‌تر آموزش نصب ووکامرس برای راه اندازی فروشگاه اینترنتی در وردپرس

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.