پیاده سازی الگوریتم Q-Learning در پایتون – راهنمای گام به گام

در مطالب پیشین «مجله تم آف» با انواع آموزشهای پایتون ازجمله پیادهسازی اندیکاتور مکدی و پیادهسازی اندیکاتور شاخص قدرت نسبی RSI در پایتون آشنا شدیم. در این مطلب قصد داریم نحوه پیاده سازی الگوریتم Q-Learning در پایتون را یاد بگیریم. البته همه کدهای پیاده سازی الگوریتم Q-Learning در پایتون در قالب یک فایل زیپ و پیش از شروع آن برای دانلود در اختیار شما قرار میگیرد. اما با توجه به آموزشی بودن این مطلب، بخشهای مختلف کدها بررسی خواهند شد.

دانلود فایل آماده پیاده سازی الگوریتم Q-Learning در پایتون
با توجه به پیچیدگی کد و پیادهسازی مرحله به مرحله آن، کد نهایی برای پیاده سازی الگوریتم Q-Learning در پایتون در قالب فایل zip در لینک زیر قرار داده میشود.
- برای دانلود فایل آماده پیاده سازی الگوریتم Q-Learning در پایتون + اینجا کلیک کنید.
دسته بندی روش های یادگیری
پیش از بررسی پیاده سازی الگوریتم Q-Learning در پایتون باید گفت که به طور کلی میتوان اکثر روشهای یادگیری ماشین را در 3 دسته زیر گنجاند:
- یادگیری بدون ناظر یا نظارت نشده (Unsupervised Learning): در این روشها ورودیهای مشخصی به مدل داده میشود و بدون داشتن هر گونه برچسب (Label) و هدف (Target)، مدل خروجی مورد نیاز را تولید میکند. برای مثال شناسایی مقادیر دورافتاده (Outlier Detection) به کمک شبکههای عصبی Auto Encoder، خوشهبندی (Clustering) به کمک الگوریتم K-Means و کاهش ابعاد توسط تحلیل مولفه اساسی (Principal Component Analysis یا PCA) جزء این دسته از مدلها است.
- یادگیری با ناظر یا نظارت شده (Supervised Learning): در این روشها مدل با دریافت مجموعه دادهای شامل ورودی و خروجی متناظر، سعی میکند ارتباط بین آنها را یاد گرفته و بهترین پیشبینی ممکنه را انجام دهد. برای مثال رگرسیون (Regression) انجام شده توسط پرسپترونهای چندلایه (Multi-Layer Perceptron یا MLP) و طبقهبندی (Classification) انجام شده توسط الگوریتم K-نزدیکترین همسایه (K-Nearest Neighbors یا KNN) جز این روشها است.
- یادگیری تقویتی (Reinforcement Learning): در این روشها یک عامل (Agent) وجود دارد که باید روش صحیح تصمیمگیری در شرایط مختلف را یاد بگیرد. این یادگیری با استفاده از فرآیند پاداش صورت میگیرد، به گونهای که عامل یاد میگیرد در هر شرایط (State) هر رفتار (Action) دارای چه کیفیتی (Quality) است. برای مثال یادگیری بازی شطرنج توسط شبکههای عصبی مصنوعی، رانندگی ماشینهای خودران و رباتهای با توانایی راه رفتن، این گونه روشهای یادگیری را مورد استفاده قرار میدهند. توجه داشته باشید که غالب تواناییهایی که انسانها در طول زندگی خود یاد میگیرند، جزء این دسته است.
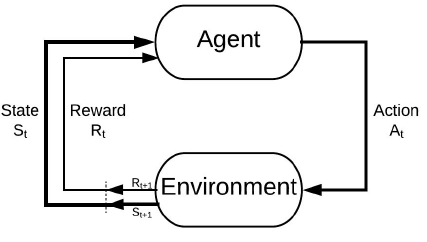
در شکل بالا یک نمای کلی از روش کار الگوریتمهای یادگیری تقویتی را مشاهده میکنید. عامل در ابتدای مسئله در شرایط$$S_{1}$$قرار دارد. براساس شرایط یک تصمیم گرفته و عمل $$A_{1}$$ را انجام میدهد. این عمل عامل به محیط برگردانده میشود و تغییراتی در شرایط ایجاد میشود. محیط در واکنش به عملِ عامل، شرایط جدید ($$S_{2}$$) و پاداش دریافتی از عمل انجام شده ($$R_{2}$$) را برمیگرداند. این عمل تا جایی تکرار میشود که عامل به انتهای Episode برسد.
هر Episode با یک شرایط ابتدایی (Initial State) شروع میشود و به یک شرایط انتهایی (Terminal State) ختم میشود. توجه داشته باشید که بعضاً به دلیل جلوگیری از انجام گامهای بسیار زیاد، یک عدد نیز به عنوان بیشینه تعداد گام تعیین میشود و قبل از اینکه به شرایط انتهایی برسیم Episode به انتها میرسد.
در این آموزش یکی از سادهترین روشهای یادگیری تقویتی یعنی Q-Learning را مورد بررسی قرار میدهیم و سپس پیادهسازی کنیم. حرف Q از ابتدای کلمه Quality به معنی کیفیت برداشته شده است. توجه داشته باشید که هر عمل در یک شرایط خاصی بهترین انتخاب ممکن است. برای مثال غذا خوردن به تنهایی یک عمل با کیفیت خوب یا بد نیست، اما غذا خوردن در شرایطی که گرسنه هستیم یک عمل با کیفیت خوب است. درحالیکه همان عمل غذا خوردن در شرایطی که سیر باشیم یک عمل با کیفیت پایین است. به همین دلیل کیفیت با توجه به شرایط موجود و عملی که میخواهیم انجام دهیم تعیین میشود.
در Q-Learning یک نگاشت از State و Action به Q داریم که در سادهترین حالت در یک جدول ذخیره میشود که به آن Q-Table گفته میشود. جدول زیر یک مثال ساده از Q-Table است:
| عمل | |||
| شرایط↓ | غذا خوردن | هیچکدام | غذا نخوردن |
| سیر | $$-1$$ | $$0$$ | $$+1$$ |
| هیچکدام | $$0$$ | $$+1$$ | $$0$$ |
| گرسنه | $$+1$$ | $$0$$ | $$-1$$ |
توجه داشته باشید که باید تمامی شرایط و تمامی عملها در این جدول وجود داشته باشند. اگر فردی بخواهد براساس جدول فوق تصمیم بگیرد، ابتدا شرایط فعلی خود را تعیین میکند. سپس در سطر مورد نظر عملی که بیشترین q را دارد را انجام میدهد. برای مثال اگر فرد نه گرسنه و نه سیر باشد، سطر دوم انتخاب میشود. در این سطر بیشترین q برابر با +1 بوده و مربوط به هیچکدام است.
روش یادگیری مقادیر Q برای پیاده سازی الگوریتم Q-Learning در پایتون
این جدول در ابتدای یادگیری عامل، مقادیر ثابت (برای مثال 0) یا تصادفی به خود میگیرد و به مرور زمان مقادیر آن تنظیم میشود. برای تنظیم این مقادیر، عبارت ریاضیاتی زیر استفاده میشود:
$$Q(s, a)^{text {new }} leftarrow Q(s, a)^{o l d}+alphaleft[r+gamma max _{a^{prime}} Qleft(s^{prime}, a^{prime}right)-Q(s, a)^{o l d}right]$$
در رابطه بالا
- $$s$$: شرایط موجود
- $$a$$: عمل انجام شده
- $$Q(s, a)^{text {old }}$$: کیفیت انجام عمل مورد نظر در شرایط فعلی قبل از به روز کردن مقادیر
- $$ Q(s, a)^{n e w}$$: کیفیت انجام عمل مورد نظر در شرایط فعلی بعد از به روز کردن مقادیر
- $$r$$: پاداش حاصل
- $$ sprime$$: شرایط جدید
- $$aprime$$: عملیاتهای ممکن در شرایط جدید
- $$alpha$$: نرخ یادگیری
- $$gamma$$: نرخ تخفیف
این عبارت به شکل زیر نیز نوشته میشود:
$$Qleft(s_{t}, a_{t}right)^{n e w} leftarrow Qleft(s_{t}, a_{t}right)^{o l d}+alphaleft[r+gamma max _{a_{t+1}} Qleft(s_{t+1}, a_{t+1}right)-Qleft(s_{t}, a_{t}right)^{o l d}right]$$
توجه داشته باشید که تغییرات حاصل در هر بار اعمال این معادله به شکل زیر خواهد بود:
$$alphaleft[r+gamma max _{a^{prime}} Qleft(s^{prime}, a^{prime}right)-Q(s, a)right]$$
به بخش داخل براکت Temporal Difference گفته میشود. این عبارت اختلاف پاداش مورد انتظار از مقدار فعلی را نشان میدهد. تا زمانی که مقدار این عبارت به $$0$$ همگرا نشود، مقادیر Q-Table بهروزرسانی خواهند شد.
ضرایب مهم در فرمول برای پیاده سازی الگوریتم Q-Learning
به بخش داخل براکت Temporal Difference گفته میشود. این عبارت اختلاف پاداش مورد انتظار از مقدار فعلی را نشان میدهد. تا زمانی که مقدار این عبارت به 0 همگرا نشود، مقادیر Q-Table بهروزرسانی خواهند شد.
$$Q(s, a)^{text {new }} leftarrow(1-alpha) Q(s, a)^{o l d}+alphaleft[r+gamma max _{a^{prime}} Qleft(s^{prime}, a^{prime}right)right]$$
با توجه به این فرم از رابطه، میتوان موارد گفته شده را تایید کرد. مقدار جدید $$Q(s, a)$$ در واقع یک میانگین وزندار از مقدار قدیمی آن و مقدار برآورد شده برای مقدار آن در گام فعلی است. توجه داشته باشید که $$r$$ نشاندهنده ارزش فعلی و $$max _{a^{prime}} Qleft(s^{prime}, a^{prime}right)$$ نشاندهنده ارزش مورد انتظار در گام بعدی است. مقدار پیشنهادی برای نرخ یادگیری اغلب عدد $$0.1$$ است، اما با توجه به شرایط محیط و مسئله ممکن است مقدار بهینه غیر از $$0.1$$ باشد.
نرخ تخفیف که با $$gamma$$ نشان داده میشود، عددی بین 0 و 1 است که اغلب عددی در بازه $$[0.9,0.95]$$ انتخاب میشود. اگر این نرخ بزرگتر از 1 باشد، مقادیر Q واگرا (Diverge) خواهد شد که مطلوب ناست. برای مقادیر زیاد نرخ تخفیف، عامل آیندهنگر بوده و برای به دست آوردن پاداشهای بزرگ در گامهای بعدی، در گامهای فعلی متحمل ضرر خواهد بود. در عکس این حالت، اگر نرخ تخفیف کوچک باشد، عامل نزدیکبین (Myopic) بوده و بدون توجه به آینده، تنها در گامهای فعلی به دنبال کسب بیشترین پاداش خواهد بود.
نحوه پیاده سازی الگوریتم Q-Learning در پایتون
در ادامه میتوانیم پیاده سازی الگوریتم Q-Learning در پایتون را شروع کنیم. به این منظور ابتدا کتابخانههای مورد نیاز را فراخوانی میکنیم:
import numpy as np
import colorama as col
import matplotlib.pyplot as pltکتابخانه Numpy برای محاسبات، ذخیره مقادیر Q و تولید اعداد تصادفی استفاده خواهد شد. کتابخانه Colorama برای نوشتن متون با رنگ دلخواه استفاده خواهد شد. کتابخانه Matplotlib نیز برای رسم نمودار محیط، نمودار عملکرد عامل در طول زمان و مسیر حرکت عامل استفاده خواهد شد.
حال تنظیمات زیر را نیز در ابتدای برنامه لحاظ میکنیم:
np.random.seed(0)
plt.style.use('ggplot')
برای پیاده سازی الگوریتم Q-Learning در پایتون نیاز به یک محیط نیز داریم. در این مقاله قصد داریم محیط Frozen Lake را استفاده کنیم. این محیط یک دنیای دو بُعدی است برخی نقاط آن یخزده و سالم است. در مقابل برخی نقاط نیز وجود دارند که حفره بوده و در صورتی که عامل وارد این نقاط شود، از بین رفته و یک پاداش منفی خواهد گرفت. هدف عامل نیز رساندن خود به نقطه انتهایی است که یک پاداش مثبت بزرگی برای آن دارد.
به این منظور پیادهسازی محیط و عامل، یک کلاس تعریف میکنیم:
class WORLD:حال اولین متد (Method) یعنی متد سازنده را ایجاد میکنیم:
def __init__(self,
H:int,
W:int,
nEpisode:int=600,
mStep:int=120,
LR:float=1e-1,
Gamma:float=9.9e-1,
eps0:float=9.8e-1,
eps1:float=0):
این متد در ورودی 8 مقدار دریافت میکند که 6 مورد از آنها مقدار پیشفرض دارند. این 8 ورودی به ترتیب موارد زیر را تنظیم میکنند:
- H: این عدد ارتفاع محیط دو بُعدی را تعیین میکند.
- W: این عدد عرض محیط دو بُعدی را تعیین میکند.
- nEpisode: این عدد تعداد اپیزودهای آموزش عامل را تعیین میکند. مقدار پیشفرض این ورودی برابر با 600 تعیین شده است. زیاد بودن این ورودی امکان یادگیری بیشتر محیط را فراهم میکند درحالیکه ممکن است مشکلاتی نیز با خود به همراه داشته باشد.
- mStep: این عدد بیشترین تعداد گام در هر Episode را تعیین میکند. اگر عامل به این تعداد گام برسد بدون آنکه به هدف مسئله دست یافته باشد یا وارد حفره شده باشد، آن Episode به اتمام میرسد. مقدار این ورودی به صورت پیشفرض 120 تعیین شده است. با افزایش سایز محیط، مقدار این ورودی نیز باید افزایش یابد، زیرا زیاد بودن آن به عامل امکان جستجو یا Exploration را میدهد. از طرفی در برخی مسائل اگر از مقدار مشخصی کمتر باشد، مانع از رسیدن عامل به هدف میشود و یک عامل محدودکننده محسوب میشود.
- LR: این عدد نشاندهنده نرخ یادگیری است که در رابطه مربوط به بهروزرسانی Q استفاده شد. مقدار پیشفرض این ورودی 0٫1 تعیین شده است که اغلب نتیجه خوبی دارد. کوچک بودن بیش از اندازه این عدد میتواند باعث کندی یادگیری یا حتی عدم یادگیری عامل شود.
- Gamma: این عدد نشاندهنده نرخ تخفیف است. مقدار پیشفرض این ورودی برابر با 0٫99 تعیین شده است. با بزرگ شده محیط، پیچیدگی آن افزایش مییابد و عامل نیاز به انجام اعمال بیشتری دارد تا از نقطه شروع به نقطه هدف برسد. بنابراین بزرگ بودن الزامی است. در محیطهای کوچک با اندازه 4×4 یا 5×5 میتواند مقدار را کمتر در نظر گرفت.
- eps0: مقدار اولیه اپسیلون را نشان میدهد. این عدد اغلب در بازه $$[0.9,1]$$ انتخاب میشود.
- eps1: مقدار نهایی اپسیلون را نشان میدهد. این عدد اغلب در بازه $$[0,0.01]$$ انتخاب میشود.
متغیر اپسیلون چیست؟
در پیاده سازی الگوریتم Q-Learning در پایتون برای انتخاب عمل در هر شرایط، از یک سیاست (Policy) استفاده میکنیم. یک سیاست تعیین میکند که با داشتن مقادیر Q برای هر عمل در یک شرایط، کدامیک باید انتخاب شود. یکی از این سیاستها، سیاست حریصانه (Greedy Policy) است. این سیاست در هر شرایط، عملی را پیشنهاد میکند که بیشترین کیفیت یا Q را دارد. برای مثال اگر داشته باشیم:
$$begin{aligned}
&Q(s, 1)=2 \
&Q(s, 2)=2.1 \
&Q(s, 3)=-1 \
&Q(s, 4)=0
end{aligned}$$
در این شرایط، سیاست حریصانه عمل 2 را پیشنهاد میدهد، چراکه بیشترین کیفیت را دارد. سیاست حریصانه در صورتی که یک جواب نسبتاً مطلوب پیدا کند، تا انتها آن را انتخاب میکند و از آن بیشترین استفاده را میکند که به آن Exploitation گفته میشود. مشکلی که وجود دارد، ندادن شانس به سایر اعمالی است که ممکن است بتوانند بهتر عمل کنند. برای مثال ممکن است در مثال فوق عمل 1 دارای کیفیت واقعی برابر با 5 داشته باشد اما به دلیل نداده شدن فرصت کافی، کشف نشود.
به همین دلیل سیاست حریصانه همواره خوب نیست و دارای نقایصی است. سیاست دیگری که دقیقاً در نقطه مخالف قرار دارد، سیاست تصادفی (Random Policy) است. این سیاست در هر شرایط، بدون توجه به کیفیت اعمال، یکی را به صورت تصادفی پیشنهاد میدهد. این سیاست برعکس سیاست حریصانه، کاملاً بر روی Exploration تمرکز میکند و به هر عمل شانس یکسانی میدهد. از این جهت که برخی اعمال پس از گذر تعداد مشخصی Episode، ارزش حدودی خود را نشان میدهند و برای انتخاب شدن بهینه نیستند، سیاست تصادفی نیز آنچنان بهینه نبوده و نمیتواند یک سیاست مناسبی باشد.
برای رفع این مشکل، و ترکیب Exploration و Exploitation با یکدگیر برای ایجاد یک تعادل، سیاست جدیدی به نام Epsilon-Greedy ایجاد شد. در این روش یک متغیر به نام اپسیلون تعریف میشود که در ابتدای یادگیری مقداری نزدیک به 1 و در انتها مقداری نزدیک به 0 دارد. این متغیر تعادل بین جستجو و بهرهبرداری را تنظیم میکند. سیاست Epsilon-Greedy به شکل زیر تصمیمگیری میکند:
$$a_{t}=left{begin{array}{l}
max _{a} Q_{t}left(s_{t}, aright) quad text { W. } mathrm{p} (1-epsilon) \
text { Random Action } quad text { W }.p epsilon
end{array}right.$$
این عبارت بیان میکند، سیاست Epsilon-Greedy، در زمان یا گام t، اگر عامل در شرایط $$S_{t}$$ قرار داشته باشد و مقادیر $$Q_{2}$$ را داشته باشیم، با احتمال $$1-epsilon$$ عملی را پیشنهاد میکند که بیشترین کیفیت را دارد و با احتمال $$epsilon$$ یک عمل کاملاً تصادفی را پیشنهاد میدهد. این اتفاق باعث میشود که با زیاد بودن اپسیلون، عامل به سمت جستجو برود که ابتدای یادگیری مسئله مطلوب است. در مقابل با کم شدن مقدار اپسیلون، عامل رفتارهای حریصانهتر از خود نشان میدهد که باعث میشود عامل به سمت بهرهبرداری برود که این حالت نیز در انتهای یادگیری مسئله مطلوب است.
بنابراین باید با گذر زمان اپسیلون کاهش یابد (Decay) که میتواند به شکل نمایی یا خطی باشد.
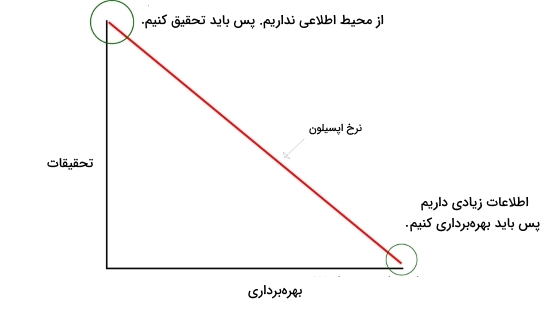
نمودار فوق به خوبی این تعادل را که توسط اپسیلون ایجاد میشود نشان میدهد.
در ورودی اخیر مربوط به متد سازنده، مقدار اولیه و نهایی اپسیلون را تنظیم میکنند.
حال ورودیهای دریافت شده در ورودی را داخل شی (Object) به عنوان Attribute ذخیره میکنیم:
def __init__(self,
H:int,
W:int,
nEpisode:int=600,
mStep:int=120,
LR:float=1e-1,
Gamma:float=9.9e-1,
eps0:float=9.8e-1,
eps1:float=0):
self.H = H
self.W = W
self.nEpisode = nEpisode
self.mStep = mStep
self.LR = LR
self.Gamma = Gamma
self.eps0 = eps0
self.eps1 = eps1
به این ترتیب تمامی موارد ذخیره میشوند. حال باید برخی تنظیمات را در رابطه با شی اعمال کنیم که برخی جز قراردادهای مربوط به محیط هستند و برخی جز متغیرهای مورد نیاز در ادامه برنامه. برای این کار متد ApplySettings را در انتهای متد سازنده فراخوانی میکنیم:
def __init__(self,
H:int,
W:int,
nEpisode:int=600,
mStep:int=120,
LR:float=1e-1,
Gamma:float=9.9e-1,
eps0:float=9.8e-1,
eps1:float=0):
self.H = H
self.W = W
self.nEpisode = nEpisode
self.mStep = mStep
self.LR = LR
self.Gamma = Gamma
self.eps0 = eps0
self.eps1 = eps1
self.ApplySettings()
حال باید این متد را تعریف کنیم:
def ApplySettings(self):این متد هیچ ورودی ندارد و تنها برخی موارد را اعمال و ذخیره میکند. اولین مورد که باید اعمال شود، حرکات عامل است. عامل میتواند در چهار جهت بالا، راست، پایین و چپ حرکت کند. بنابراین در یک دیکشنری (Dictionary) شماره هر عمل و تغییرات موقعیت را ذخیره میکنیم:
def ApplySettings(self):
self.Transition = {0: [-1, 0], # Up
1: [0, +1], # Right
2: [+1, 0], # Down
3: [0, -1]} # Left
به این ترتیب با داشتن شماره هر عمل، میتوانیم تغییرات موقعیت را محاسبه کنیم. توجه داشته باشید که موقعیت عامل و نقاط در مختصات دکارتی نبوده و براساس شمارش ریاضیاتی در آرایهها است. بنابراین محور عمودی در اولویت بوده و شمارش عکس دارد، بنابراین حرکت در جهات بالا و پایین شامل تغییرات در بُعد اول است.
تعداد کل اعمال نیز باید به عنوان یک متغیر ذخیره شود تا بعداً در صورت نیاز استفاده شود:
def ApplySettings(self):
self.Transition = {0: [-1, 0], # Up
1: [0, +1], # Right
2: [+1, 0], # Down
3: [0, -1]} # Left
self.nAction = len(self.Transition)
مورد دیگری که باید تعیین شود، پاداش اتفاقاتی است که عامل رقم میزند. برای این منظور نیز از یک دیکشنری استفاده میکنیم:
def ApplySettings(self):
self.Transition = {0: [-1, 0], # Up
1: [0, +1], # Right
2: [+1, 0], # Down
3: [0, -1]} # Left
self.nAction = len(self.Transition)
self.Rewards = {'Outside': -1, # Trying To Go Outside
'Move': -0.1, # Normal Move
'Hole': -2, # Falling In Hole
'Goal': +100} # Reaching Goalبه این ترتیب:
- اگر عامل سعی کند از مرزهای محیط عبور کند (انجام حرکت اشتباه و رخ ندادن هرگونه جابهجایی)، 1 واحد جریمه میشود.
- اگر عامل یک حرکت معمولی انجام دهد (به هدف نرسد و در حفره سقوط نکند)، به دلیل هزینه حرکت 0.1 واحد جریمه میشود.
- اگر عامل در حفره سقوط کند، 2 واحد جریمه میشود.
- اگر عامل به هدف برسد، 100 واحد پاداش میگیرد.
توجه داشته باشید که نسبت بین پاداشها و جریمهها بسیار مهم است و باید به درستی انتخاب شود. چراکه یادگیری عامل براساس این پاداشها است و براساس آنها تربیت میشود.
حال باید شمارهگزاری نقاط را نیز انجام دهیم. به این منظور نیز از یک دیکشنری دیگر استفاده میکنیم که با دادن نوع نقطه، کد مربوطه را دریافت کنیم:
def ApplySettings(self):
self.Transition = {0: [-1, 0], # Up
1: [0, +1], # Right
2: [+1, 0], # Down
3: [0, -1]} # Left
self.nAction = len(self.Transition)
self.Rewards = {'Outside': -1, # Trying To Go Outside
'Move': -0.1, # Normal Move
'Hole': -2, # Falling In Hole
'Goal': +100} # Reaching Goal
self.Type2Code = {'Frozen': 0,
'Start': 1,
'Hole': 2,
'Goal': 3,
'Outside': 4}
به این ترتیب:
- نقاطی که یخزده هستند با کد 0 نشان داده خواهند شد.
- نقطه شروع با کد 1 نشان داده میشود.
- حفرهها با کد 2 نشان داده میشوند.
- هدف با کد 3 نشان داده میشود.
- نقاط بیرون از محیط با کد 4 نشان داده میشوند.
تنظیماتی که تا به اینجا اعمال شدند، جزء قراردادهای ما برای کدنویسی بودند. توجه داشته باشید که این موارد را میتوان به اشکال دیگر نیز توصیف و کدنویسی کرد.
حال دو متغیر جدید با نامهای MinQ و MaxQ ایجاد میکنیم. مقداردهی اولیه Qها نیز براساس این مقادیر خواهد بود:
def ApplySettings(self):
self.Transition = {0: [-1, 0], # Up
1: [0, +1], # Right
2: [+1, 0], # Down
3: [0, -1]} # Left
self.nAction = len(self.Transition)
self.Rewards = {'Outside': -1, # Trying To Go Outside
'Move': -0.1, # Normal Move
'Hole': -2, # Falling In Hole
'Goal': +100} # Reaching Goal
self.Type2Code = {'Frozen': 0,
'Start': 1,
'Hole': 2,
'Goal': 3,
'Outside': 4}
self.MinQ = -1
self.MaxQ = +1توجه داشته باشید که در شرایط این مسئله، مقدار Q در بازه $$[-2,+100]$$ عادی است اما به دلیل اینکه ممکن است در ابتدای مسئله عامل برخی از Qها را بیش از اندازه تغییر دهد، بعداً ممکن است جبران کردن آن نیاز به مراحل بیشتری داشته باشد. در حالت کلی این مقادیر باید متناسب با بزرگی پاداشها باشند اما به سمت میانگین متمرکزتر باشند.
با توجه به اینکه الگوریتم به تعداد nEpisode بار تکرار میشود، باید در یک متغیر شماره Episode را ذخیره کنیم. با توجه به اینکه هنوز آموزش عامل شروع نشده است، مقدار $$-1$$ مناسب خواهد بود:
def ApplySettings(self):
self.Transition = {0: [-1, 0], # Up
1: [0, +1], # Right
2: [+1, 0], # Down
3: [0, -1]} # Left
self.nAction = len(self.Transition)
self.Rewards = {'Outside': -1, # Trying To Go Outside
'Move': -0.1, # Normal Move
'Hole': -2, # Falling In Hole
'Goal': +100} # Reaching Goal
self.Type2Code = {'Frozen': 0,
'Start': 1,
'Hole': 2,
'Goal': 3,
'Outside': 4}
self.MinQ = -1
self.MaxQ = +1
self.Episode = -1
حال باید مقادیر Epsilon را نیز برای هر Episode محاسبه کنیم. قصد داریم یک کاهش خطی (Linear Decay) استفاده کنیم، به همین دلیل تابع numpy.linspace مناسب است:
def ApplySettings(self):
self.Transition = {0: [-1, 0], # Up
1: [0, +1], # Right
2: [+1, 0], # Down
3: [0, -1]} # Left
self.nAction = len(self.Transition)
self.Rewards = {'Outside': -1, # Trying To Go Outside
'Move': -0.1, # Normal Move
'Hole': -2, # Falling In Hole
'Goal': +100} # Reaching Goal
self.Type2Code = {'Frozen': 0,
'Start': 1,
'Hole': 2,
'Goal': 3,
'Outside': 4}
self.MinQ = -1
self.MaxQ = +1
self.Episode = -1
self.Epsilons = np.linspace(start=self.eps0,
stop=self.eps1,
num=self.nEpisode)
به این ترتیب به تعداد nEpisode نقطه با فاصله یکسان در بازه $$[epsilon_0,epsilon_1]$$ ایجاد میشود. در هر Episode از اجرای کد، Epsilon متناظر با آن استفاده خواهد شد.
حال باید یک آرایه برای ذخیره نقشه محیط ایجاد کنیم. این نقشه موقعیت محل شروع، محل هدف و نقاط حاوی حفره را ذخیره خواهد کرد. به این منظور از numpy.zeros استفاده میکنیم:
def ApplySettings(self):
self.Transition = {0: [-1, 0], # Up
1: [0, +1], # Right
2: [+1, 0], # Down
3: [0, -1]} # Left
self.nAction = len(self.Transition)
self.Rewards = {'Outside': -1, # Trying To Go Outside
'Move': -0.1, # Normal Move
'Hole': -2, # Falling In Hole
'Goal': +100} # Reaching Goal
self.Type2Code = {'Frozen': 0,
'Start': 1,
'Hole': 2,
'Goal': 3,
'Outside': 4}
self.MinQ = -1
self.MaxQ = +1
self.Episode = -1
self.Epsilons = np.linspace(start=self.eps0,
stop=self.eps1,
num=self.nEpisode)
self.Map = np.zeros((self.H, self.W), dtype=np.int32)
توجه داشته باشید که مقادیر این آرایه باید اعداد صحیح (Integer) باشند.
حال یک دیکشنری برای ذخیره مقادیر Q ایجاد میکنیم. کلیدهای (Key) آن نشاندهنده هر State و مقادیر آن (Value) آرایههایی به طول 4 خواهند بود که نشاندهنده کیفیت هر عمل هستند:
def ApplySettings(self):
self.Transition = {0: [-1, 0], # Up
1: [0, +1], # Right
2: [+1, 0], # Down
3: [0, -1]} # Left
self.nAction = len(self.Transition)
self.Rewards = {'Outside': -1, # Trying To Go Outside
'Move': -0.1, # Normal Move
'Hole': -2, # Falling In Hole
'Goal': +100} # Reaching Goal
self.Type2Code = {'Frozen': 0,
'Start': 1,
'Hole': 2,
'Goal': 3,
'Outside': 4}
self.MinQ = -1
self.MaxQ = +1
self.Episode = -1
self.Epsilons = np.linspace(start=self.eps0,
stop=self.eps1,
num=self.nEpisode)
self.Map = np.zeros((self.H, self.W), dtype=np.int32)
self.Q = {}
حال یک لیست و یک آرایه نیز برای ذخیره پاداش عامل در طول آموزش ایجاد میکنیم:
def ApplySettings(self):
self.Transition = {0: [-1, 0], # Up
1: [0, +1], # Right
2: [+1, 0], # Down
3: [0, -1]} # Left
self.nAction = len(self.Transition)
self.Rewards = {'Outside': -1, # Trying To Go Outside
'Move': -0.1, # Normal Move
'Hole': -2, # Falling In Hole
'Goal': +100} # Reaching Goal
self.Type2Code = {'Frozen': 0,
'Start': 1,
'Hole': 2,
'Goal': 3,
'Outside': 4}
self.MinQ = -1
self.MaxQ = +1
self.Episode = -1
self.Epsilons = np.linspace(start=self.eps0,
stop=self.eps1,
num=self.nEpisode)
self.Map = np.zeros((self.H, self.W), dtype=np.int32)
self.Q = {}
self.ActionLog = []
self.EpisodeLog = np.zeros(self.nEpisode)
لیست ActionLog پاداش هر عمل را به ترتیب در خود ذخیره میکند. آرایه EpisodeLog نیز مجموع پاداش حاصل در هر Episode را ذخیره میکند. متد ApplySettings تا به اینجا کامل شده و عملکرد خود را خواهد داشت.
متد بعدی که لازم است پیادهسازی شود، برای نماش نقشه یا همان self.Map است. به این منظور متدی با نام ShowMap را ایجاد میکنیم:
def ShowMap(self):برای رسم آرایه میتوانیم از matplotlib.pyplot.imshow استفاده کنیم:
def ShowMap(self):
plt.imshow(self.Map)
plt.title('World Map')
plt.xlabel('Width')
plt.ylabel('Height')
plt.show()
نکته مهمی که باید توجه کرد، این است که محور افقی به عنوان بُعد دوم در نظر گرفته شده و برابر با عرض خواهد بود. محور عمودی نیز به عنوان بُعد اول در نظر گرفته شده و برابر با ارتفاع است.
متد بعدی که باید پیادهسازی شود، AddStart است. این متد با گرفتن مختصات مورد نظر برای محل شروع، آن را به نقشه محیط اضافه خواهد کرد:
def AddStart(self, h:int, w:int):
self.Start = np.array([h, w])
self.Map[h, w] = self.Type2Code['Start']
این متد به شکل بالا خواهد بود. توجه داشته باشید که محل شروع باید خود به تنهایی نیز ذخیره شود، زیرا در انتهای هر Episode عامل به محل شروع برمیگردد. برای مقداردهی در نقشه نیز بهتر است از دیکشنری self.Type2Code استفاده کنید تا خوانایی کد بالاتر رفته و احتمال خطا کم باشد.
متد بعدی نیز برای اضافه کردن محل هدف استفاده خواهد شد. این متد نیز به شکل زیر تعریف میشود:
def AddGoal(self, h:int, w:int):
self.Map[h, w] = self.Type2Code['Goal']
توجه داشته باشید که چون محل هدف مورد نیاز ناست و صرفاً تغییر مقدار مربوط به آن در آرایه نقشه کفایت میکند، آن را در شی ذخیره نمیکنیم.
متد بعدی نیز مشابه دو متد قبلی است، با این تفاوت که مجموعهای نقاط را به شکل آرایه دریافت خواهد کرده و این نقاط را در نقشه محیط به عنوان حفره مشخص خواهد کرد:
def AddHoles(self, Holes:np.ndarray):
for i in Holes:
self.Map[i[0], i[1]] = self.Type2Code['Hole']
به این ترتیب 3 متد مورد نیاز برای ایجاد محیط کامل میشود.
حال باید متدی تعریف کنیم که بتواند در ابتدای هر Episode موقعیت و شرایط عامل را به حالت اولیه برگرداند. به این منظور متد ResetState را ایجاد میکنیم و به شکل زیر تعریف میکنیم:
def ResetState(self):
self.Position = self.Start
self.UpdateState()
در اولین خط، موقعیت عامل را به محل شروع برمیگردانیم. در خط دوم متد دیگری را فراخوانی میکنیم که براساس self.Position شرایط عامل را تعیین میکند.
برای متد UpdateState یک تابع ایجاد میکنیم و یک متغیر خالی از جنس رشته (String) را ایجاد میکنیم:
def UpdateState(self):
self.s = ''
با توجه به اینکه عامل 8 خانه در اطراف خود را میتواند ببیند، دو حلقه ایجاد میکنیم تا در هر بُعد 3 مقدار را ایجاد کنند:
def UpdateState(self):
self.s = ''
for i in [-1, 0, +1]:
for j in [-1, 0, +1]:
حلقه اول در بعد ارتفاع، یکی بالا، هم ارتفاع و یکی پایین را ایجاد میکند. حلقه دوم نیز در بعد عرض سمت راست، همعرض و سمت چپ را ایجاد میکند. بنابراین با ترکیب آنها، 9 موقعیت در نقشه قابل بررسی خواهد بود. تنها موردی که باید به آن توجه کرد، در برخی مسائل محل قرارگیری عامل نیز با کد مشخصی نشان داده میشود. در اینگونه مسائل، باید کد مربوط به محل قرارگیری عامل در State آورده نشود، چراکه تنها یک مقدار ممکن دارد.
حال موقعیت را برای تکتک حالتها حساب میکنیم:
def UpdateState(self):
self.s = ''
for i in [-1, 0, +1]:
for j in [-1, 0, +1]:
h = self.Position[0] + i
w = self.Position[1] + j
با توجه به اینکه برخی از این موقعیتها ممکن است بیرون از مرزهای محیط باشد، باید با یک شرط این حالات را بررسی کنیم. اگر موقعیت حاصل درست باشد، کد مربوطه از نقشه برداشته شده و به انتهای self.s اضافه میشود. در غیر اینصورت، کد مربوط به کلید Outside به انتهای آن اضافه میشود:
def UpdateState(self):
self.s = ''
for i in [-1, 0, +1]:
for j in [-1, 0, +1]:
h = self.Position[0] + i
w = self.Position[1] + j
if h in range(self.H) and w in range(self.W):
self.s += str(self.Map[h, w])
else:
self.s += str(self.Type2Code['Outside'])
به این ترتیب برای عامل در هر نقطه، یک State قابل تعریف خواهد بود که شامل 9 عدد چیده شده پشت سر هم است. نکته مهمی که باید مورد توجه قرار داد، امکان ایجاد شرایط جدیدی هست که تا به اینجا مشاهده نشدهاند. در Q-Table برای هر State باید یک سطر وجود داشته باشد. بنابراین در انتهای این تابع، یک شرط اضافه میکنیم. این شرط در صورتی که به شرایط جدیدی بربخورد، برای این شرایط یک Q تصادفی جدید در self.Q ایجاد میکند:
def UpdateState(self):
self.s = ''
for i in [-1, 0, +1]:
for j in [-1, 0, +1]:
h = self.Position[0] + i
w = self.Position[1] + j
if h in range(self.H) and w in range(self.W):
self.s += str(self.Map[h, w])
else:
self.s += str(self.Type2Code['Outside'])
if self.s not in self.Q:
self.Q[self.s] = np.random.uniform(low=self.MinQ,
high=self.MaxQ,
size=self.nAction)
به این ترتیب در صورت نیاز، دیکشنری self.Q بهروزرسانی میشود.
متد بعدی که باید پیادهسازی شود، مربوط به تصمیمگیری است. این متد در هر شرایط، با توجه به سیاست تعریف شده، یه عمل را انتخاب کرده و برمیگرداند. متد را به شکل زیر تعریف میکنیم:
def Decide(self, Policy:str):
در ورودی، سیاست مورد استفاده نیز دریافت میشود. اولین سیاست که پیادهسازی میکنیم، سیاست تصادفی است. در صورتی که Policy ورودی برابر با R باشد، یک عمل به صورت تصادفی انتخاب میشود:
def Decide(self, Policy:str):
if Policy == 'R': # Random Policy
a = np.random.randint(low=0, high=4)
سیاست بعدی نیز سیاست حریصانه است و در صورتی که Policy ورودی برابر با G باشد استفاده میشود:
def Decide(self, Policy:str):
if Policy == 'R': # Random Policy
a = np.random.randint(low=0, high=4)
elif Policy == 'G': # Greedy Policy
t = self.Q[self.s]
a = np.argmax(t)
در این بخش 2 سطر به ترتیب اعمال زیر را انجام میدهند:
- برای شرایط فعلی (s) مقادیر Q استخراج میشود و در t ذخیره میشود.
- تابع argmax آرایه t را دریافت میکند و اندیسی (Index) که بیشترین مقدار را دارد را به عنوان عمل منتخب در a ذخیره میکند.
حال باید سیاست Epsilon-Greedy را نیز اضافه کنیم، به این منظور باید Policy ورودی برابر با EG باشد. در این شرایط یک عدد تصادفی از 0 تا 1 تولید شده و براساس آن یکی از دو سیاست قبلی اجرا میشود:
def Decide(self, Policy:str):
if Policy == 'R': # Random Policy
a = np.random.randint(low=0, high=4)
elif Policy == 'G': # Greedy Policy
t = self.Q[self.s]
a = np.argmax(t)
elif Policy == 'EG': # Epsilon-Greedy Policy
if np.random.rand() به این ترتیب هر سه سیاست پیادهسازی شده و به درستی کار خواهند کرد. توجه داشته باشید که برای پیادهسازی سیاست Epsilon-Greedy از توابع بازگشتی (Recursive Function) استفاده کردیم تا هم کد سادهتر بوده و هم از خوانایی بیشتری برخوردار باشد.
حال متد بعدی که باید پیادهسازی شود، مربوط به جابهجایی عامل است. با انتخاب هر کدام از 4 عمل، عامل ممکن است در یکی از جهات حرکت کند، به همین دلیل باید متد یک متد نیز تعریف شود که در این شرایط عامل را جابهجا کند و شرایط را بهروزرسانی کند. این متد در ورودی مکان جدید عامل را دریافت خواهد کرد:
def Move2(self, NewPosition:np.ndarray):
حال self.Position را تغییر میدهیم و با توجه به تغییر موقعیت، State عامل نیز تغییر میکند، بنابراین نیاز است تا متد UpdateState نیز فراخوانی شود:
def Move2(self, NewPosition:np.ndarray):
self.Position = NewPosition
self.UpdateState()
به این ترتیب با این متد قابلیت جابهجایی عامل فراهم خواهد شد.
حال باید متدی تعریف کنیم که با گرفتن عمل منتخب، آن را در محیط اعمال کرده و نتایج را برگرداند. این متد در ورودی عمل انتخاب شده را دریافت میکند و در خروجی، پاداش حاصل، شرایط بعدی، اتمام یا عدم اتمام Episode و پیام را انتقال میدهد. در خلال کار این متد نیز باید موقعیت عامل در صورت نیاز بهروزرسانی شود. این متد در ورودی عمل انتخاب شده را دریافت میکند:
def DoAction(self, a:int):
حال باید موقعیت حاصل پس از حرکت را محاسبه کنیم. تغییرات به ازای هر عمل، در دیکشنری self.Transition ذخیره شده است. بنابراین مقدار متناظر در این دیکشنری را به موقعیت فعلی اضافه میکنیم تا موقعیت بعدی محاسبه شود:
def DoAction(self, a:int):
h, w = self.Position + self.Transition[a]
حال یک متغیر برای ذخیره اتمام یا عدم اتمام Episode ایجاد میکنیم که به صورت پیشفرض False است:
def DoAction(self, a:int):
h, w = self.Position + self.Transition[a]
done = False
در صورتی که عامل به حفره سقوط کند یا به هدف برسد، مقدار done به True تغییر خواهد یافت.
متغیر دیگری نیز برای ذخیره پیام حاصل از این حرکت ایجاد میکنیم. این متغیر نیز به صورت پیشفرض مقدار None به خود میگیرد و در صورت نیاز مقداردهی خواهد شد:
def DoAction(self, a:int):
h, w = self.Position + self.Transition[a]
done = False
message = None
با توجه به اینکه نیاز است در انتهای این تابع، موقعیت عامل بهروزرسانی شود، باید موقعیت جدید نیز به شکل یک آرایه ذخیره شود. ممکن است این متغیر نیز بعداً تغییر کند:
def DoAction(self, a:int):
h, w = self.Position + self.Transition[a]
done = False
message = None
NewPosition = np.array([h, w])
در صورتی که عامل از محیط خارج شود، جریمه مربوط به Outside را دریافت خواهد کرد. با توجه به اینکه این موقعیت صحیح ناست، باید موقعیت جدید برابر با موقعیت فعلی باشد. همچنین در این شرایط Episode به اتمام نمیرسد و هیچ پیامی برای انتقال وجود ندارد:
def DoAction(self, a:int):
h, w = self.Position + self.Transition[a]
done = False
message = None
NewPosition = np.array([h, w])
if h not in range(self.H) or w not in range(self.W):
r = self.Rewards['Outside']
NewPosition = self.Position
در صورتی که شرط فوق صدق نکند، به این معنی است که عامل از محیط خارج نشده، بنابراین میتوانیم نوع خانه مقصد را بررسی کنیم و براساس آن پاداش عامل را تعیین کنیم. اولین حالت، شرایطی را بررسی میکنیم که عامل به یک خانه «یخزده» (Frozen) یا محل شروع (Start) رفته است. در این شرایط Episode به اتمام نمیرسد و پیامی برای انتقال وجود ندارد:
def DoAction(self, a:int):
h, w = self.Position + self.Transition[a]
done = False
message = None
NewPosition = np.array([h, w])
if h not in range(self.H) or w not in range(self.W):
r = self.Rewards['Outside']
NewPosition = self.Position
else:
if self.Map[h, w] in [self.Type2Code['Start'], self.Type2Code['Frozen']]:
r = self.Rewards['Move']
حال باید حالت مربوط به سقوط در حفره را بررسی کنیم. در این شرایط Episode به اتمام میرسد، عامل پاداش مربوط به Hole را دریافت میکند و یک پیام مبنی بر شکست عامل در رسیدن به هدف ایجاد میشود:
def DoAction(self, a:int):
h, w = self.Position + self.Transition[a]
done = False
message = None
NewPosition = np.array([h, w])
if h not in range(self.H) or w not in range(self.W):
r = self.Rewards['Outside']
NewPosition = self.Position
else:
if self.Map[h, w] in [self.Type2Code['Start'], self.Type2Code['Frozen']]:
r = self.Rewards['Move']
elif self.Map[h, w] == self.Type2Code['Hole']:
r = self.Rewards['Hole']
done = True
message = col.Fore.RED + 'Failed To Reach Goal.' + col.Fore.RESET
توجه داشته باشید که با استفاده از کتابخانه Colorama رنگ متن را به قرمز تغییر میدهیم، اما برای جلوگیری از تغییر رنگ متنهای بعدی، باید بعد از متن رنگ را به حالتی قبلی برگردانیم.
تنها حالت باقیمانده، مربوط به موفقیت عامل در رسیدن به هدف است. در این حالت عامل پاداش Goal را دریافت میکند، Episode مربوطه به اتمام میرسد و یک پیام مبنی بر موفقیت عامل ایجاد میشود:
def DoAction(self, a:int):
h, w = self.Position + self.Transition[a]
done = False
message = None
NewPosition = np.array([h, w])
if h not in range(self.H) or w not in range(self.W):
r = self.Rewards['Outside']
NewPosition = self.Position
else:
if self.Map[h, w] in [self.Type2Code['Start'], self.Type2Code['Frozen']]:
r = self.Rewards['Move']
elif self.Map[h, w] == self.Type2Code['Hole']:
r = self.Rewards['Hole']
done = True
message = col.Fore.RED + 'Failed To Reach Goal.' + col.Fore.RESET
elif self.Map[h, w] == self.Type2Code['Goal']:
r = self.Rewards['Goal']
done = True
message = col.Fore.GREEN + 'Reached Goal.' + col.Fore.RESET
به این ترتیب متغیرهای مورد نیاز به درستی مقداردهی خواهند شد. حال باید با استفاده از متد Move2 که قبلاً پیادهسازی شد، عامل را به موقعیت نهایی منتقل کنیم و پاداش حاصل را نیز در self.ActionLog ذخیره کنیم:
def DoAction(self, a:int):
h, w = self.Position + self.Transition[a]
done = False
message = None
NewPosition = np.array([h, w])
if h not in range(self.H) or w not in range(self.W):
r = self.Rewards['Outside']
NewPosition = self.Position
else:
if self.Map[h, w] in [self.Type2Code['Start'], self.Type2Code['Frozen']]:
r = self.Rewards['Move']
elif self.Map[h, w] == self.Type2Code['Hole']:
r = self.Rewards['Hole']
done = True
message = col.Fore.RED + 'Failed To Reach Goal.' + col.Fore.RESET
elif self.Map[h, w] == self.Type2Code['Goal']:
r = self.Rewards['Goal']
done = True
message = col.Fore.GREEN + 'Reached Goal.' + col.Fore.RESET
self.Move2(NewPosition)
self.ActionLog.append(r)در نهایت برای استفادههای بعدی، پاداش حاصل، شرایط جدید، اتمام یا عدم اتمام Episode و پیام ایجاد شده را برمیگردانیم:
def DoAction(self, a:int):
h, w = self.Position + self.Transition[a]
done = False
message = None
NewPosition = np.array([h, w])
if h not in range(self.H) or w not in range(self.W):
r = self.Rewards['Outside']
NewPosition = self.Position
else:
if self.Map[h, w] in [self.Type2Code['Start'], self.Type2Code['Frozen']]:
r = self.Rewards['Move']
elif self.Map[h, w] == self.Type2Code['Hole']:
r = self.Rewards['Hole']
done = True
message = col.Fore.RED + 'Failed To Reach Goal.' + col.Fore.RESET
elif self.Map[h, w] == self.Type2Code['Goal']:
r = self.Rewards['Goal']
done = True
message = col.Fore.GREEN + 'Reached Goal.' + col.Fore.RESET
self.Move2(NewPosition)
self.ActionLog.append(r)
return r, self.s, done, message
به این ترتیب به کمک این متد میتوانیم حرکت عامل در محیط را شبیهسازی و پاداش را محاسبه کنیم.
متد بعدی که نیاز داریم تا پیاده کنیم، مربوط به بهروزرسانی Q است. این متد در ورودی، شرایط، عمل انتخاب شده، پاداش حاصل و شرایط نهایی را دریافت میکند:
def UpdateQ(self, s:str, a:int, r:float, s2:str):
سپس با توجه به رابطه گفته شده در ابتدای مطلب، مقدار را بهروزرسانی میکند. ابتدا Temporal Difference را محاسبه میکنیم:
def UpdateQ(self, s:str, a:int, r:float, s2:str):
TD = r + self.Gamma * self.Q[s2].max() - self.Q[s][a]
حال میتوانیم TD را به نرخ یادگیری اضافه کرده، با مقدار قدیمی جمع کرده و جایگزین کنیم:
def UpdateQ(self, s:str, a:int, r:float, s2:str):
TD = r + self.Gamma * self.Q[s2].max() - self.Q[s][a]
self.Q[s][a] = self.Q[s][a] + self.LR * TDبه این ترتیب این متد میتواند پس از انجام هر عمل، مقادیر Q را تغییر داده و موجب آموزش عامل شود.
حال تنها یک متد باقی مانده تا بتوانیم آموزش عامل را کدنویسی کنیم. این متد NextEpisode نام دارد و در ابتدای هر Episode اجرا میشود تا شماره Episode را یک عدد افزایش داده و مقدار Epsilon را انتخاب کند:
def NextEpisode(self):
self.Episode += 1
self.Epsilon = self.Epsilons[self.Episode]
توجه داشته باشید که مقدار اولیه self.Episode برابر با -1 بود، بنابراین در ابتدای اولین Episode با افزایش یک واحد آن، به 0 میرسد و اولین مقدار آرایه self.Epsilons انتخاب میشود.
حال میتوانیم متد اصلی که مربوط به آموزش عامل هست را پیادهسازی کنیم. این متد تنها یک ورودی دریافت میکند که مربوط به سیاست مورد استفاده است و به صورت پیشفرض Epsilon-Greedy استفاده خواهد شد:
def Train(self, Policy:str='EG'):
حال یک حلقه ایجاد میکنیم تا برای هر Episode کدهای مربوط به آموزش را اجرا کند:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
سپس در اولین اقدام، متد NextEpisode را فراخوانی میکنیم تا شروع Episode بعدی رخ دهد:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
حال شماره Episode را نمایش میدهیم تا در حین کار الگوریتم، از وضعیت آن مطلع باشیم:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
print(f'Episode {self.Episode + 1} / {self.nEpisode}')
قبل از شروع گامها، موقعیت عامل را با محل شروع تغییر میدهیم و شرایط را Reset میکنیم. به این منظور متد ResetState را فراخوانی میکنیم:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
print(f'Episode {self.Episode + 1} / {self.nEpisode}')
self.ResetState()
حال موقعیت عامل را در متغیری به نام s ذخیره میکنیم:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
print(f'Episode {self.Episode + 1} / {self.nEpisode}')
self.ResetState()
s = self.s
یک حلقه به ازای تمامی گامهای ممکن ایجاد میکنیم و در هر گام یک عمل را انتخاب میکنیم. به این منظور از متد Decide استفاده میکنیم:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
print(f'Episode {self.Episode + 1} / {self.nEpisode}')
self.ResetState()
s = self.s
for _ in range(self.mStep):
a = self.Decide(Policy)
حال عمل انتخاب شده را انجام میدهیم و، پاداش، موقعیت جدید، اتمام یا عدم اتمام Episode و پیام حاصل را دریافت میکنیم:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
print(f'Episode {self.Episode + 1} / {self.nEpisode}')
self.ResetState()
s = self.s
for _ in range(self.mStep):
a = self.Decide(Policy)
r, s2, done, message = self.DoAction(a)حال میتوانیم مقادیر Q را با استفاده از متد UpdateQ بهروزرسانی کنیم:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
print(f'Episode {self.Episode + 1} / {self.nEpisode}')
self.ResetState()
s = self.s
for _ in range(self.mStep):
a = self.Decide(Policy)
r, s2, done, message = self.DoAction(a)
self.UpdateQ(s, a, r, s2)
به این ترتیب این گام به اتمام رسیده و عامل آموزش میبینید. حال باید پاداش حاصل را به آرایه self.EpisodeLog اضافه کنیم:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
print(f'Episode {self.Episode + 1} / {self.nEpisode}')
self.ResetState()
s = self.s
با توجه به اینکه شرایط جدید حاصل، برابر با شرایط در گام بعدی است، مقدار s را نیز با s2 تعیین میکنیم:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
print(f'Episode {self.Episode + 1} / {self.nEpisode}')
self.ResetState()
s = self.s
for _ in range(self.mStep):
a = self.Decide(Policy)
r, s2, done, message = self.DoAction(a)
self.UpdateQ(s, a, r, s2)
self.EpisodeLog[i] += r
s = s2
حال در انتهای حلقه بررسی میکنیم که آیا به انتهای Episode رسیدهایم یا نه و در صورت درست بودن، حلقه را break میکنیم:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
print(f'Episode {self.Episode + 1} / {self.nEpisode}')
self.ResetState()
s = self.s
for _ in range(self.mStep):
a = self.Decide(Policy)
r, s2, done, message = self.DoAction(a)
self.UpdateQ(s, a, r, s2)
self.EpisodeLog[i] += r
s = s2
if done:
break
پس از اتمام Episode باید بررسی کنیم که آیا خروج از حلقه به دلیل وقوع شرایط انتهایی بوده (Terminal State) یا بیشینه گام ممکن طی شده است. در صورتی که شرایط انتهایی رخ داده باشد، پیام حاصل را نمایش میدهیم و در صورتی که اینگونه نباشد، پیامی مبتی بر رسیدن به بیشینه تعداد گام نمایش میدهیم:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
print(f'Episode {self.Episode + 1} / {self.nEpisode}')
self.ResetState()
s = self.s
for _ in range(self.mStep):
a = self.Decide(Policy)
r, s2, done, message = self.DoAction(a)
self.UpdateQ(s, a, r, s2)
self.EpisodeLog[i] += r
s = s2
if done:
break
if done:
print(message)
else:
print(col.Fore.BLUE + 'Maximum Steps Reached.' + col.Fore.RESET)
به این ترتیب دلیل اتمام هر Episode با رنگ مخصوص خود نمایش داده میشود. در انتها نیز مجموع پاداش آن Episode را نمایش میدهیم و سپس یک خط افقی به کمک متد HL رسم میکنیم:
def Train(self, Policy:str='EG'):
for i in range(self.nEpisode):
self.NextEpisode()
print(f'Episode {self.Episode + 1} / {self.nEpisode}')
self.ResetState()
s = self.s
for _ in range(self.mStep):
a = self.Decide(Policy)
r, s2, done, message = self.DoAction(a)
self.UpdateQ(s, a, r, s2)
self.EpisodeLog[i] += r
s = s2
if done:
break
if done:
print(message)
else:
print(col.Fore.BLUE + 'Maximum Steps Reached.' + col.Fore.RESET)
print(col.Fore.YELLOW + f'Reward: {self.EpisodeLog[i]:.4f}' + col.Fore.RESET)
self.HL()
به این ترتیب متد Train که مهمترین متد است، پیادهسازی شده و آماده کار است. برای متد HL نیز از کد زیر استفاده میشود:
def HL(self, s:str='_', n:int=65):
print(s * n)
حال یک تابع نیاز داریم تا مقادیر لیست self.ActionLog را در قالب یک نمودار نمایش دهد. به این منظور یک متد با نام PlotActionLog ایجاد میکنیم که در طول یک میانگین متحرک (Moving Average یا MA) را نیز دریافت میکند:
def PlotActionLog(self, L:int=200):توجه داشته باشید که استفاده از میانگین متحرکها برای نشان دادن روند بهبود عملکرد الگوریتمها به خصوص در حوزه یادگیری تقویتی مرسوم است. برای آشنایی با میانگینهای متحرک، میتوانید به مطلب میانگین متحرک چیست؟ + پیادهسازی Moving Average در پایتون مراجعه کنید.
حال در ابتدا یک میانگین متحرک ساده (Simple Moving Average یا SMA) از self.ActionLog محاسبه میکنیم:
def PlotActionLog(self, L:int=200):
M = self.SMA(self.ActionLog, L)
آرایه دیگری نیز برای ذخیره مقادیر محور افقی ایجاد میکنیم. به این منظور تابع numpy.arange مناسب است:
def PlotActionLog(self, L:int=200):
M = self.SMA(self.ActionLog, L)
T = np.arange(start=1,
stop=len(self.ActionLog) + 1,
step=1)
حال میتوانیم نمودار مورد نظر را رسم کنیم:
def PlotActionLog(self, L:int=200):
M = self.SMA(self.ActionLog, L)
T = np.arange(start=1,
stop=len(self.ActionLog) + 1,
step=1)
plt.plot(T,
self.ActionLog,
ls='-',
lw=1.2,
c='teal',
label='Reward')
plt.plot(T[-M.size:],
M,
ls='-',
lw=1.4,
c='crimson',
label=f'SMA({L})')
plt.title('Agent Reward On Each Action')
plt.xlabel('Action')
plt.ylabel('Reward')
plt.legend()
plt.show()
توجه داشته باشید که طول میانگین متحرک حاصل کمتر از طول لیست اولیه است به همین دلیل بخشی از ابتدای آرایه T مورد استفاده قرار نمیگیرد.
متد بعدی نیز مشابه قبلی است با این تفاوت که برای رسم self.EpisodeLog استفاده خواهد شد. به این منظور، متد زیر استفاده خواهد شد:
def PlotEpisodeLog(self, L:int=30):
M = self.SMA(self.EpisodeLog, L)
T = np.arange(start=1,
stop=World.nEpisode + 1,
step=1)
plt.plot(T,
self.EpisodeLog,
ls='-',
lw=1.2,
c='teal',
label='Reward')
plt.plot(T[-M.size:],
M,
ls='-',
lw=1.4,
c='crimson',
label=f'SMA({L})')
plt.title('Agent Reward On Each Episode')
plt.xlabel('Episode')
plt.ylabel('Reward')
plt.legend()
plt.show()
به این ترتیب دو متد اخیر برای مصورسازی روند آموزش عامل، به خوبی عمل خواهند کرد. در طول پیادهسازی این دو متد، از متد SMA استفاده شد. این متد نیز به شکل زیر پیادهسازی میشود:
def SMA(self, S:Union[np.ndarray, list], L:int):
M = np.convolve(S, np.ones(L) / L, mode='valid')
return M
توجه داشته باشید که در متد PlotActionLog یک لیست به عنوان ورودی اول داده میشود و متد PlotEpisodeLog یک آرایه Numpy در ورودی داده میشود. به همین دلیل بهتر است هر دو جنس در ورودی تعریف شود. برای داشتن یک میانگین متحرک ساده، به هر روز وزن برابر با $$frac{1}{L}$$ میدهیم.
برای استفاده از Union باید کد زیر را به ابتدای برنامه اضافه کنیم:
from typing import Unionتا به اینجا تمامی متدهای مورد نیاز برای آموزش و مصورسازی آموزش آن پیادهسازی شدهاند. برای تست (Test) و بررسی عملکرد عامل، یک متد دیگر باید پیادهسازی کنیم تا یک Episode را از ابتدا تا انتها شبیهسازی کرده و در نهایت نموداری از روش حرکت عامل را نشان دهد.
این متد در ورودی سیاست مورد نظر و نمایش یا عدم نمایش نمودار حرکت را دریافت میکند. با توجه به اینکه پس از اتمام Train، مدل به خوبی آموزش دیده است، استفاده از سیاست Epsilon-Greedy بیمعنی بوده و سیاست Greedy بهترین گزینه است:
def Test(self, Policy:str='G', Plot:bool=True):
حال در اولین اقدام یک خط افقی رسم کرده و سپس پیامی مبنی بر Test عامل نمایش میدهیم:
def Test(self, Policy:str='G', Plot:bool=True):
self.HL()
print('Testing Agent:')
حال مشابه قبل شرایط را به شروع برگردانده، یک لیست برای ذخیره موقعیت عامل در هر گام ایجاد کرده و یک متغیر برای ذخیره پاداشها ایجاد میکنیم:
def Test(self, Policy:str='G', Plot:bool=True):
self.HL()
print('Testing Agent:')
self.ResetState()
Positions = [self.Position]
Reward = 0
از لیست Positions برای رسم مسیر حرکت عامل استفاده خواهیم کرد. حال به تعداد گامها یک حلقه ایجاد میکنیم:
def Test(self, Policy:str='G', Plot:bool=True):
self.HL()
print('Testing Agent:')
self.ResetState()
Positions = [self.Position]
Reward = 0
for _ in range(self.mStep):
حال یک عمل را انتخاب میکنیم و آن را انجام میدهیم:
def Test(self, Policy:str='G', Plot:bool=True):
self.HL()
print('Testing Agent:')
self.ResetState()
Positions = [self.Position]
Reward = 0
for _ in range(self.mStep):
a = self.Decide(Policy)
r, _, done, message = self.DoAction(a)
توجه داشته باشید که میتوانیم به جای متغیرهایی که نیاز نداریم، در حلقه for و خروجی توابع از Underscore استفاده کنیم.
حال موقعیت جدید عامل را به لیست اضافه و پاداش دریافتی را نیز به مقدار کل اضافه میکنیم:
def Test(self, Policy:str='G', Plot:bool=True):
self.HL()
print('Testing Agent:')
self.ResetState()
Positions = [self.Position]
Reward = 0
for _ in range(self.mStep):
a = self.Decide(Policy)
r, _, done, message = self.DoAction(a)
Positions.append(self.Position)
Reward += r
حال مشابه متد Train شرایط اتمام را بررسی و پیامهای مورد نیاز را نمایش میدهیم:
def Test(self, Policy:str='G', Plot:bool=True):
self.HL()
print('Testing Agent:')
self.ResetState()
Positions = [self.Position]
Reward = 0
for _ in range(self.mStep):
a = self.Decide(Policy)
r, _, done, message = self.DoAction(a)
Positions.append(self.Position)
Reward += r
if done:
break
if done:
print(message)
else:
print(col.Fore.BLUE + 'Maximum Steps Reached.' + col.Fore.RESET)
print(col.Fore.YELLOW + f'Reward: {Reward:.4f}' + col.Fore.RESET)
حال مسیر طی شده را نیز در خروجی نشان میدهیم:
def Test(self, Policy:str='G', Plot:bool=True):
self.HL()
print('Testing Agent:')
self.ResetState()
Positions = [self.Position]
Reward = 0
for _ in range(self.mStep):
a = self.Decide(Policy)
r, _, done, message = self.DoAction(a)
Positions.append(self.Position)
Reward += r
if done:
break
if done:
print(message)
else:
print(col.Fore.BLUE + 'Maximum Steps Reached.' + col.Fore.RESET)
print(col.Fore.YELLOW + f'Reward: {Reward:.4f}' + col.Fore.RESET)
Positions = np.array(Positions)
print(f'Path:n{Positions}')
به این ترتیب متون مورد نیاز نشان داده خواهد شد. با توجه به اینکه کاربر در ورودی مقدار Plot را به False تغییر داده باشد یا نه، یک نمودار نیز برای مسیر حرکت عامل رسم میکنیم:
def Test(self, Policy:str='G', Plot:bool=True):
self.HL()
print('Testing Agent:')
self.ResetState()
Positions = [self.Position]
Reward = 0
for _ in range(self.mStep):
a = self.Decide(Policy)
r, _, done, message = self.DoAction(a)
Positions.append(self.Position)
Reward += r
if done:
break
if done:
print(message)
else:
print(col.Fore.BLUE + 'Maximum Steps Reached.' + col.Fore.RESET)
print(col.Fore.YELLOW + f'Reward: {Reward:.4f}' + col.Fore.RESET)
Positions = np.array(Positions)
print(f'Path:n{Positions}')
if Plot:
xs = []
ys = []
cs = []
for i in range(self.H):
for j in range(self.W):
xs.append(j)
ys.append(self.H - i - 1)
cs.append(World.Map[i, j])
plt.scatter(xs,
ys,
s=1960,
c=cs,
marker='s')
for i in range(len(Positions) - 1):
x1 = Positions[i][1]
y1 = self.H - Positions[i][0] - 1
x2 = Positions[i + 1][1]
y2 = self.H - Positions[i + 1][0] - 1
dx = x2 - x1
dy = y2 - y1
plt.arrow(x1,
y1,
dx,
dy,
lw=2,
head_width=0.12,
head_length=0.1,
length_includes_head=True,
color='r')
plt.title('World Map + Agent Path')
plt.xlabel('Width')
plt.ylabel('Height')
plt.xlim(-0.5, self.W - 0.5)
plt.ylim(-0.5, self.H - 0.5)
plt.show()
self.HL()
به این ترتیب این متد و بخشی از پیاده سازی الگوریتم Q-Learning در پایتون به اتمام میرسد. توجه داشته باشید که با تغییر سایز محیط، مقدار s=1960 باید تغییر کند.
تا به اینجا پیادهسازی محیط و عامل به اتمام رسید. حال میتوانیم یک شی از کلاس پیادهسازی شده ایجاد کنیم:
World = WORLD(6, 8)به این ترتیب یک محیط 6×8 ایجاد میشود.
حال محل شروع عامل و محل هدف را تعیین میکنیم:
World.AddStart(0, 0)
World.AddGoal(5, 7)
در یک آرایه نیز موقعیتهایی را به عنوان حفره در نظر میگیریم و به عنوان ورودی متد AddHoles استفاده میکنیم:
Holes = np.array([[0, 2],
[1, 3],
[1, 6],
[2, 5],
[2, 6],
[3, 2],
[3, 3],
[3, 4],
[3, 6],
[4, 2],
[5, 0],
[5, 4],
[5, 6]])
World.AddHoles(Holes)
حال میتوانیم با استفاده از متد ShowMap محیط را نمایش دهیم:
World.ShowMap()که در خروجی خواهیم داشت:
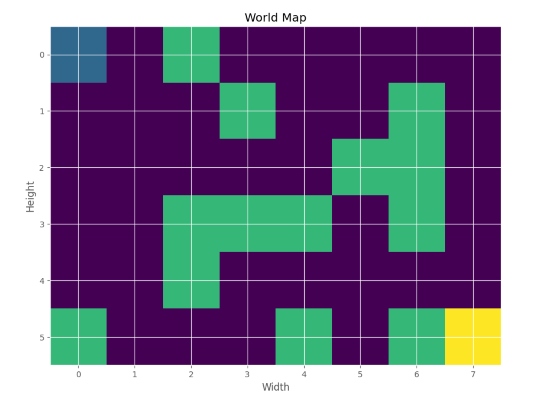
به این ترتیب مشاهده میکنیم که یک محیط با ارتفاع 6 و عرض 8 ایجاد شده است. نقطه بالا سمت چپ به عنوان محل شروع و نقطه پایین سمت راست نیز به عنوان محل هدف تعیین شده است.
حال میتوانیم متد Train را فراخوانی و عامل را آموزش دهیم:
World.Train()در حین اجرای این متد نتایجی به شکل زیر نمایش داده خواهد شد:
Episode 1 / 600
Failed To Reach Goal.
Reward: -3.3000
_______________________________________________________________
Episode 2 / 600
Failed To Reach Goal.
Reward: -2.1000
_______________________________________________________________
.
.
.
.
_______________________________________________________________
Episode 599 / 600
Reached Goal.
Reward: 98.5000
_______________________________________________________________
Episode 600 / 600
Reached Goal.
Reward: 98.5000
_______________________________________________________________
به این ترتیب مشاهده میکنیم که عامل در ابتدای آموزش به پاداشی در حدود $$-3$$ دست یافته و نتوانسته خود را به هدف برساند. درحالیکه در انتهای آموزش به پاداشی در حدود $$+98$$ دست یافته و توانسته خود را به هدف برساند.
برای نمایش بهتر روند آموزش عامل، متد PlotActionLog را فراخوانی میکنیم:
World.PlotActionLog()که نمودار زیر را خواهیم داشت:
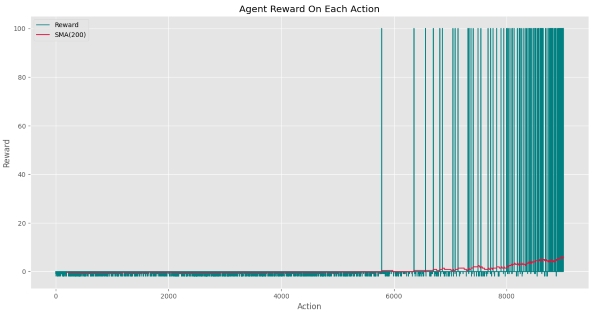
مشاهده میکنیم که تا Action شماره 5600 عامل نتوانسته پاداش مربوط به هدف دریافت کند. پس از دستیابی عامل به هدف، به مرور زمان تعداد دفعات دستیابی به هدف افزایش یافته. بهبود عملکرد عامل با شیب نمودار SMA کاملاً مشهود است. اگر تنها نمودار SMA را رسم میکردیم، نموداری به شکل زیر داشتیم:
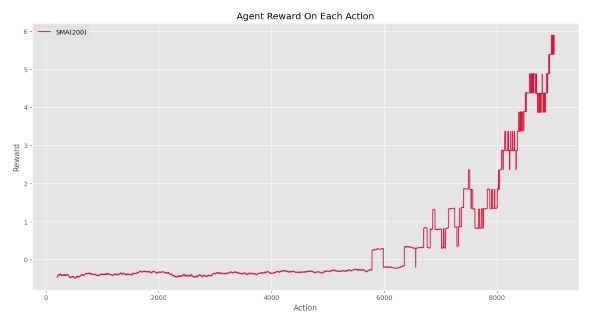
به این صورت روند بهبود میتواند آشکارتر نشان داده شود.
حال میتوانیم مجموع پاداش دریافتی در هر Episode را نیز رسم کنیم. به این منظور متد PlotEpisodeLog را فراخوانی میکنیم:
World.PlotEpisodeLog()که خواهیم داشت:
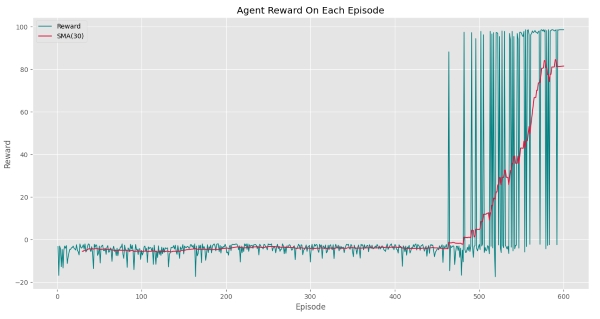
به این ترتیب مشاهده میکنیم که عامل برای اولین بار در Episode شماره 460 به هدف رسیده است و Episodeهای نهایی با احتمال بالایی هدف را یافته است. برای این تابع نیز اگر تنها SMA را رسم کنیم، خواهیم داشت:
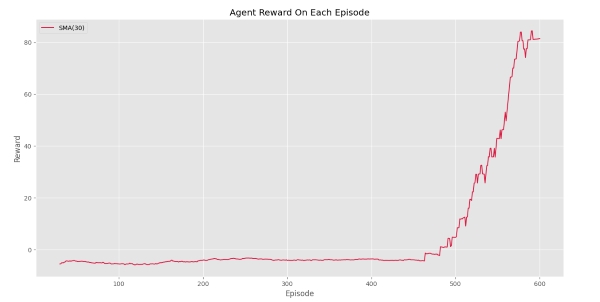
بنابراین میتوان گفت عامل در 30 Episode نهایی، به میانگین پاداش 81 دست یافته است. شروع روند افزایش پس از اولین دستیابی به هدف، نکته حائز اهمیتی است.
به این ترتیب تا به اینجا محیط را ایجاد کردیم، عامل را آموزش دادیم و روند آموزش آن را بررسی کردیم. حال میتوانیم برای بررسی عملکرد آن، از متد Test استفاده کنیم:
World.Test()که نتایج زیر را برای نمایش خواهد داد:
_______________________________________________________________
Testing Agent:
Reached Goal.
Reward: 98.5000
Path:
[[0 0]
[1 0]
[1 1]
[1 2]
[2 2]
[2 3]
[2 4]
[1 4]
[1 5]
[0 5]
[0 6]
[0 7]
[1 7]
[2 7]
[3 7]
[4 7]
[5 7]]
_______________________________________________________________
به این ترتیب مشاهده میکنیم که عامل با سیاست حریصانه توانسته به هدف برسد و مجموع پاداش 98٫5 را دریافت کند.
در بخش بعدی نیز مسیر طی شده از ابتدا تا انتها نوشته شده است که مشاهده میکنیم عامل از موقعیت [0,0] شروع کرده و در نهایت به موقعیت [5,7] رفته است. در طول این مسیر 16 بار حرکت رخ داده که 15 مورد به خانههای یخزده بوده بنابراین مجموعاً $$-1.5$$ واحد جریمه دریافت کرده است. در نهایت نیز با وارد شدن به خانه مربوط به هدف، 100 واحد پاداش دریافت کرده است که برآیند آنها برابر با 98٫5 است.
پس از متون فوق، نمودار مربوط به مسیر حرکت نیز نمایش داده میشود:
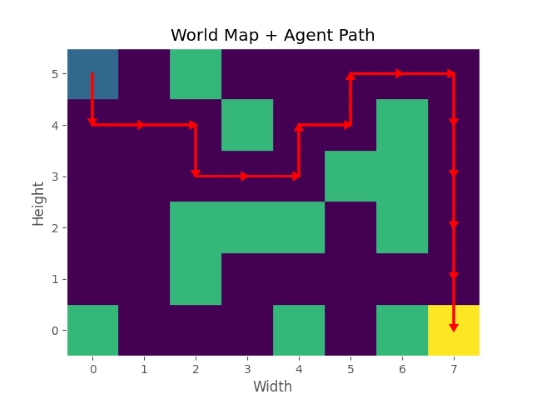
مشاهده میکنیم که عامل به درستی توانسته موانع را پشت سر گزاشته و خود را به هدف برساند. توجه داشته باشید که عامل میتوانسته مسیر سمت چپ را در پیش بگیرد که در این صورت میتوانسته به پاداش 98٫7 دست یابد که نتوانسته این مسیر را بیابد. با اینکه از سیاست Epsilon-Greedy استفاده کردهایم اما با این حال باز هم الگوریتم نتوانسته برخی جوابهای بهتر را بیابد. به همین دلیل تنظیم برخی پارامترها میتواند بسیار تاثیرگزار باشد.
به این ترتیب Test عامل نیز انجام میشود و نتایج مصورسازی میشود.
حال میتوانیم مقادیر دیکشنری Q را نیز بررسی کنیم. این دیکشنری به شکل زیر است:
'444410400': [-1.25687943, -0.65783016, -0.65562986, -1.23372197]
'444102000': [-1.03979104, -1.09468206, -0.59477318, -0.59967951]
'444020002': [+0.29634374, -0.26351692, +0.91431032, -0.71929844]
'102000000': [-0.54433654, -0.44808586, -0.53255533, -0.54120797]
'410400400': [-0.58903452, -0.58801907, -0.58944872, -1.13836360]
'020002000': [-1.08110056, -2.01113426, -0.07427464, -0.47201429]
'002000022': [-0.42448925, +0.78408723, -1.60820360, -0.42064965]
'000000002': [-0.48431727, -0.35080743, -0.48359998, -0.48269242]
'000002002': [-0.46729695, -1.60637494, -0.46477281, -0.46422842]
'002002200': [-0.43479727, -1.13044687, -0.44028859, -0.44266351]
'002200444': [-0.40743624, -0.40249768, -0.46738428, -0.91484743]
'020000444': [-1.10526592, -0.35878076, -0.55380499, -0.36138822]
'200002444': [-0.27358260, -1.01516238, -0.68549599, -0.30463211]
'000020444': [-0.21026141, +0.23761713, -0.05026497, -0.05973562]
'400400400': [-0.54604956, -0.53436127, -0.54397246, -1.10202071]
'400400420': [-0.44264515, -0.44627351, -0.87875864, -0.83483361]
'400420444': [+0.73276465, +0.95104301, +0.71160668, -0.97657183]
'200020000': [-0.01908238, -0.54517074, -0.49128704, -0.88394168]
'020000222': [-2.00004582, +2.52519731, -1.33204447, -0.34771620]
'000222200': [-0.90798538, -0.53474601, -0.30296126, +0.62993296]
'022020000': [-0.35119027, +0.36023108, +0.59106949, +0.00786722]
'000022020': [+0.22349683, +0.34381403, -0.10496826, +0.39215434]
'200002220': [+6.13765705, -1.04109472, -0.94339556, -0.27031852]
'000200002': [-0.19114477,+12.76040482, -0.22524992, -1.04379680]
'002022202': [ 0.48820246, +0.67961305, -0.54228522, -0.73210222]
'002220000': [-0.26504936, +0.41374362, +0.29906845, +0.85595233]
'222200002': [-0.74508917, +0.13477320, -0.25926015, -1.20627303]
'220000020': [-0.67157945, +2.24551302, -0.50251622, -0.22516305]
'000002022': [23.29242056, -0.58874802, -0.73992671, -0.60353149]
'444000002': [-0.67680790,+37.64495264, -0.10603322, -0.11065548]
'000020220': [+0.61430125, -0.52255267, -0.89782046, -0.44634442]
'444000200': [-0.70019777, +1.17092139, -0.30900452, -0.17270054]
'444200020': [+0.25038159, +0.21667852, -0.51914960, +0.19269019]
'444000020': [+0.06018980,+54.51406217, -0.37329739, -0.61283023]
'444004204': [+6.58803702, +0.12390761,+71.56169260, +0.01272704]
'202000202': [+0.09044980,+14.50830851, -0.26907047, -0.91165152]
'020000023': [-0.68905161, +55.1480457, +0.01236629, +0.23732694]
'022202000': [-0.23347889, -0.17917118, -0.34713062, -0.76826913]
'220020000': [-0.82416887, +0.81242591, +0.83685045, +0.99541198]
'204004234': [16.33018559, -0.85068880,100.86923522, +4.37678566]
'000202444': [+0.22885745, -0.89567038, +0.49970055, -0.06349510]
'004204204': [+0.00899245, -0.25314759,+85.60405470, -0.13699257]
'204204204': [10.34298890, +2.12406348,+94.16187470, -0.00257834]
'204204004': [+0.32074207,+14.28494421,+98.82385268, -0.15557498]
'004234444': [-0.99088386, +0.71132955, +0.97479535, +0.33488841]
'020220020': [+0.08615851, -0.75464418, -0.87251777, -0.89173430]
به این ترتیب مشاهده میکنیم که برای 46 شرایط مختلف، مقادیر Q برای 4 عمل محاسبه و ذخیره شده است.
برای مثال خانه یکی مانده به هدف را بررسی میکنیم. این خانه به شکل زیر است:
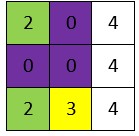
با توجه به اینکه 3 خانه سمت راست، خارج از محیط است، کد 4 را به خود میگیرند. حال اگر State را ایجاد کنید به کد زیر خواهیم رسید:
204004234
حال برای این State میتوانیم مقادیر Q را بیابیم که به شکل زیر خواهد بود:
$$204004234:[+16.33,-0.85,+100.87,+4.38]$$
برای سادگی مقادیر را تا دو رقم اعشار گرد میکنیم. حال میتوانیم به خوبی مشاهده کنیم که عمل سوم دارای بیشترین ارزش برابر با 100٫87 است. عمل شماره سوم، حرکت به سمت پایین بود که در این موقعیت، باعث حرکت عامل به هدف خواهد شد. از این روی این عمل دارای کیفیت نزدیک به 100 یعنی پاداش حاصل از دستیابی به هدف است.
سایر خانههای در مسیر رسیدن به هدف نیز دارای ارزش بالایی است.
نکات مهمی که در رابطه با الگوریتمهای یادگیری تقویتی باید به آن توجه کرد:
- پیادهسازی این الگوریتمها نسبت به سایر الگوریتمهای یادگیری ماشین سخت است بنابراین نیاز به دقت بالایی در کدنویسی دارد.
- تنظیم هایپرپارامترهای مربوط به مسئله و یادگیری عامل، از اهمیت بسیار بالایی برخوردار است، به نحوی که ممکن است با اندکی تغییر، عامل نتواند یاد بگیرد.
- یادگیری تقویتی بخش بزرگی از مهارتهای انسانی را شامل میشود، به همین دلیل نقش بسیار مهم و بزرگتری در آینده هوش مصنوعی دارد.
برای بررسی گزاره دوم، میتوان مقدار Gamma را از 0٫99 به 0٫95 تغییر داد. در این شرایط، نتیجه Test به شکل زیر خواهد بود:
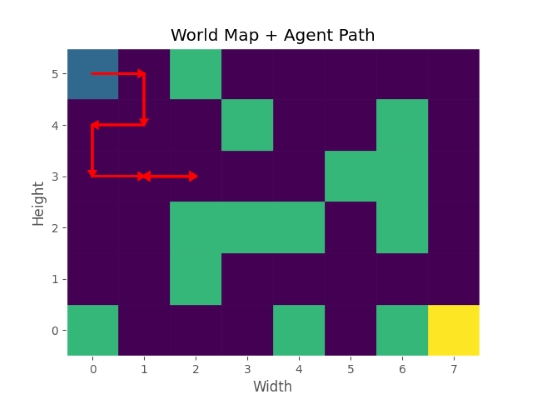
به این ترتیب مشاهده میکنیم که تغییرات کوچک در هایپرپارامترها، میتواند تا چه اندازه نتایج را تحت تاثیر قرار دهد.
همچنین اگر مقدار نرخ یادگیری یا LR را از 0٫1 به 0٫2 تغییر دهیم، نتیجه Test به شکل زیر تغییر میکند:
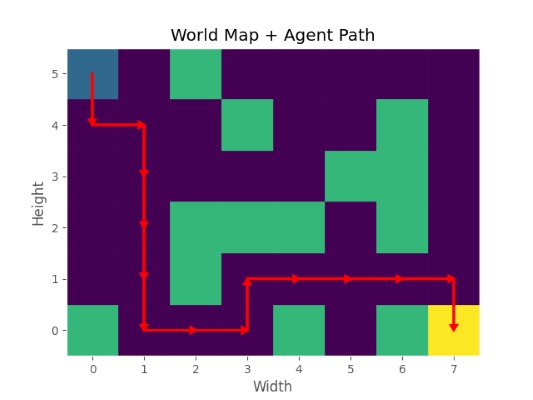
به این ترتیب عامل میتواند مسیر بهتری به سمت هدف بیابد.
مطالعه بیشتر برای پیاده سازی الگوریتم Q-Learning در پایتون
برای مطالعه بیشتر در رابطه با پیاده سازی الگوریتم Q-Learning در پایتون میتوان موارد زیر را بررسی کرد:
- اگر این پروژه بدون استفاده از شیگرایی (Object Oriented Programming یا OOP) پیادهسازی شود، چه مشکلاتی وجود خواهد داشت؟
- اگر روند کاهشی Epsilon به جای خطی (Linear Decay)، به صورت نمایی (Exponential Decay) باشد، چه اتفاقی رخ میدهد؟
- چگونه میتوان به عامل قابلیت حرکت به درون هر 8 خانه اطراف را داد؟
- اگر برای حرکت به سمت بیرون از محیط جریمهای در نظر گرفته نشود، چه مشکلی پیش خواهد آمد؟
- اگر برای محل شروع کد اختصاصی تعیین نشود و از کد 0 استفاده شود، چه اتفاقی برای سرعت یادگیری و Q-Table رخ خواهد داد؟
- اگر مقادیر MinQ و MaxQ به جای -1 و +1، برابر با -10 و +10 تعیین شود، سرعت یادگیری چگونه تغییر میکند؟
- کد مربوط به متد UpdateState را به گونهای تغییر دهید که کد مربوط به محل قرارگیری عامل را در State دخالت ندهد.
- انواع دیگری از میانگینهای متحرک نیز وجود دارد. در مورد آنها تحقیق کنید.
- اگر عامل، به جای یک مربع 3×3 به یک مربع 5×5 دید داشته باشد و بتواند در 8 جهت حرکت کند، پیچیدگی Q-Table چند برابر حالت فعلی خواهد بود؟

