پیاده سازی الگوریتم K نزدیکترین همسایه یا KNN برای رگرسیون در پایتون

در مطلب گذشته، الگوریتم K نزدیکترین همسایه (K-Nearest Neighbors یا KNN) را برای طبقهبندی (Classification) پیادهسازی کردیم. برای مطالعه میتوانید به مطلب پیاده سازی الگوریتم KNN با پایتون – راهنمای کاربردی مراجعه کنید. در این مطلب قصد داریم همان الگوریتم را برای رگرسیون (Regression) استفاده کنیم و با نحوه پیاده سازی الگوریتم K نزدیکترین همسایه آشنا شویم.

دانلود فایل پیاده سازی الگوریتم K نزدیکترین همسایه
با توجه به پیچیدگی مراحل و کدهای موجود در این الگوریتم، کد نهایی را میتوانید از لینک زیر دانلود کنید.
- برای دانلود کد نهایی پیاده سازی الگوریتم K نزدیکترین همسایه برای رگرسیون در پایتون + اینجا کلیک کنید.
روش کار الگوریتم الگوریتم K نزدیکترین همسایه
به منظور پیشبینی مقدار، با داشتن یک داده مشخص $$x$$ میتوانیم فاصله آن را از تمامی دادههای آموزش (Train) محاسبه کنیم:
$$d_{i}=operatorname{distance}left(x text{Train}_{i}, xright)$$
توجه داشته باشید که تابع فاصله میتواند انواع مختلف داشته باشد. یکی از معیارهای فاصله پرکاربرد، «فاصله مینکوسکی» (Minkowski Distance) است. این معیار به شکل زیر محاسبه میشود:
$$d(a, b)=left(sum_{i=1}^{n}left|a_{i}-b_{i}right|^{p}right)^{frac{1}{p}}$$
توجه داشته باشید که پارامتر $$p$$ میتواند اعداد مختلفی در بازه $$(0, +infty]$$ باشد. برای مثال اگر مقدار آن برابر با 1 باشد، رابطه به شکل زیر درمیآید:
$$
d(a, b)=sum_{i=1}^{n}left|a_{i}-b_{i}right|
$$
به این معیار «فاصله منهتن» (Manhattan Distance) نیز گفته میشود.
حال اگر مقدار $$p$$ برابر با 2 در نظر گرفته شود، به رابطه زیر میرسیم:
$$
d(a, b)=sqrt{sum_{i=1}^{n}left(a_{i}-b_{i}right)^{2}}
$$
به این معیار فاصله اقلیدسی (Euclidean Distance) نیز گفته میشود. برای $$p$$ دو مقدار $$1,2$$ معمولتر است.
پس از محاسبه فواصل، $$K$$ مورد از نزدیکترین همسایهها را انتخاب میکنیم. در این مرحله دو روش برای پیشبینی وجود دارد:
- به همه همسایگان وزن یکسانی میدهیم. این حالت Uniform نامیده میشود.
- به همسایههای نزدیکتر، وزن بیشتری دهیم. این حالت Distance Weighted نامیده میشود.
هر کدام از این دو روش، میتواند تحت شرایطی مناسب باشد.
برای حالت اول، پیشبینی به شکل زیر خواهد بود:
$$
y=frac{1}{K} sum_{i=1}^{K} y_{N_{i}}
$$
برای حالت دوم نیز به شکل زیر خواهیم داشت:
$$
y=sum_{i=1}^{K} w_{i} times y_{N_{i}}
$$
برای تعیین وزن همسایگان در این حالت، روشهای مختلفی وجود دارد. یکی از این روشها، استفاده از عکس فاصله است:
$$
w_{i}=frac{frac{1}{d_{N_{i}}}}{sum_{j=1}^{K} frac{1}{d_{N_{j}}}}
$$
توجه داشته باشید که چون باید مجموع وزنها برابر 1 باشه، عبارت مخرج نیز اضافه میشود. به این ترتیب، همسایگان نزدیکتر وزن بیشتری خواهند داشت و مجموع وزنها همواره برابر با 1 خواهد بود.
پیادهسازی الگوریتم
حال وارد محیط برنامهنویسی میشویم و کتابخانههای مورد نیاز را فراخوانی میکنیم:
import numpy as np
import matplotlib.pyplot as pltاز کتابخانه اول برای تولید داده، محاسبات مربوط به الگوریتم و ارزیابی نتایج استفاده خواهیم کرد. کتابخانه numpy به دلیل محاسبات برداری و توابعی متنوع کاربردی، به این منظور بسیار مناسب است.
کتابخانه دوم نیز برای رسم نمودارهای مربوط به ارزیابی مدل استفاده خواهد شد.
در ابتدا یک کلاس برای الگوریتم ایجاد میکنیم:
class KNNregression:متد سازنده
حال متد (Method) سازنده را ایجاد میکنیم. این متد 3 ورودی خواهد داشت:
- مقدار $$K$$ که نشاندهنده تعداد همسایههای مورد استفاده برای پیشبینی است. این ورودی به صورت پیشفرض برابر با ۵ است.
- شیوه وزندهی به همسایهها که میتواند Uniform یا Distance باشد. این ورودی به صورت پیشفرض برابر با Uniform خواهد بود.
- مقدار پارامتر در معیار فاصله مینوسکی که میتواند عددی در بازه گفته شده باشد. این ورودی به صورت پیشفرض برابر با ۲ خواهد بود.
حال ورودیهای دریافت شده را «شیء» (Object) ذخیره میکنیم:
def __init__(self,
K:int=5,
W:str='Uniform',
p:int=2):
self.K = K
self.W = W.lower()
self.p = p
توجه داشته باشید که ورودی $$W$$ از جنس «رشته» (String) است، بنابراین ممکن است براساس سلیقه با حروف کوچک، بزرگ یا حالتهای دیگر وارد شود. به دلیل جلوگیری از بروز مشکل در این شرایط، تمامی حروف را به حروف کوچک (Lowercase) تبدیل میکنیم و سپس ذخیره میکنیم.
متد آموزش در پیاده سازی الگوریتم K نزدیکترین همسایه
برای استفاده از الگوریتم، در ابتدا باید آن را آموزش دهیم. در این مرحله مجموعه داده آموزش را دریافت میکنیم:
def Train(self,
trX:np.ndarray,
trY:np.ndarray):
توجه داشته باشید که باید هر دو ورودی trX و trY باید از جنس آرایه Numpy باشند. حال مجموعه داده (Dataset) دریافتی را در شیء ذخیره میکنیم:
def Train(self,
trX:np.ndarray,
trY:np.ndarray):
self.trX = trX.copy()
self.trY = trY.copy()
توجه داشته باشید که بهتر است نسخه کپی شده از این مجموعه داده ذخیره شود. با توجه به اینکه مدل دارای هیچگونه پارامتری (Parameter) برای آموزش نیست، فرآیند یادگیری تنها شامل ذخیره مجموعه داده خواهد بود.
متد پیشبینی برای پیاده سازی الگوریتم K نزدیکترین همسایه
حال باید یک متد دیگری ایجاد کنیم که پس از آموزش مدل، بتواند با دریافت ورودیهای جدید، خروجی مدل را برگرداند. این متد در ورودی آرایه $$X$$ را دریافت کرده و در خروجی آرایه $$P$$ را برخواهد گرداند:
def Predict(self,
X:np.ndarray) -> np.ndarray:
در اولین گام، تعداد داده را استخراج میکنیم. به این منظور از متد shape که مربوط به آرایههای Numpy است استفاده میکنیم:
def Predict(self,
X:np.ndarray) -> np.ndarray:
n = X.shape[0]
حال یک آرایه ستونی خالی برای ذخیره مقادیر پیشبینی شده ایجاد میکنیم. به این منظور با استفاده از numpy.zeros یک آرایه خالی ایجاد میکنیم:
def Predict(self,
X:np.ndarray) -> np.ndarray:
n = X.shape[0]
P = np.zeros((n, 1))
حال یک حلقه برای دادههای ورودی ایجاد میکنیم:
def Predict(self,
X:np.ndarray) -> np.ndarray:
n = X.shape[0]
P = np.zeros((n, 1))
for i, x in enumerate(X):
با توجه به اینکه هم اندیس (Index) داده را نیاز داریم و هم مقدار آن را، از enumerate استفاده میکنیم. حال فواصل و مقادیر همسایگان را دریافت میکنیم. به این منظور از متد GetNeighbors استفاده میکنیم که بعداً پیادهسازی خواهیم کرد:
def Predict(self,
X:np.ndarray) -> np.ndarray:
n = X.shape[0]
P = np.zeros((n, 1))
for i, x in enumerate(X):
dNs, yNs = self.GetNeighbors(x)
به این ترتیب متد GetNeighbors با دریافت بردار ورودی $$x$$ فاصله $$K$$ همسایه نزدیک و مقدار متغیر هدف همان همسایگان را برمیگرداند. حال باید وزن هر همسایه محاسبه شود. به این منظور از متد دیگری به نام GetWeights استفاده خواهیم کرد. این متد فواصل $$K$$ همسایه نزدیک را دریافت خواهد کرد:
def Predict(self,
X:np.ndarray) -> np.ndarray:
n = X.shape[0]
P = np.zeros((n, 1))
for i, x in enumerate(X):
dNs, yNs = self.GetNeighbors(x)
w = self.GetWeights(dNs)
حال میتوانید بین دو آرایه $$yNs$$ و $$w$$ یک ضرب عضو به عضو (Element-Wise) انجام دهیم تا مقدار خروجی حاصل شود. به این منظور تابع numpy.multiply مناسب خواهد بود. مقدار حاصل را در سطر $$i$$ از آرایه $$P$$ ذخیره میکنیم:
def Predict(self,
X:np.ndarray) -> np.ndarray:
n = X.shape[0]
P = np.zeros((n, 1))
for i, x in enumerate(X):
dNs, yNs = self.GetNeighbors(x)
w = self.GetWeights(dNs)
P[i, 0] = np.multiply(yNs, w).sum()
توجه داشته باشید که حاصل عملیات تابع numpy.multiply یک آرایه خواهد بود و باید مجموع درایهها محاسبه شود.
حال آرایه $$P$$ را در خروجی برمیگردانیم:
def Predict(self,
X:np.ndarray) -> np.ndarray:
n = X.shape[0]
P = np.zeros((n, 1))
for i, x in enumerate(X):
dNs, yNs = self.GetNeighbors(x)
w = self.GetWeights(dNs)
P[i, 0] = np.multiply(yNs, w).sum()
return P
به این ترتیب متد مربوط به پیشبینی کامل میشود.
متد یافتن همسایهها در پیاده سازی الگوریتم K نزدیکترین همسایه
این متد که با نام GetNeighbors استفاده شده است، به منظور تعیین $$K$$ نزدیکترین استفاده خواهد شد. در ورودی یک بردار دریافت خواهد شد و در خروجی دو آرایه برگردانده میشود، بنابراین خروجی یک تاپل (Tuple) خواهد بود:
def GetNeighbors(self,
x:np.ndarray) -> tuple:
حال باید فاصله بردار $$x$$ را از تمامی دادههای آموزش محاسبه میکنیم. به این منظور اختلاف به بردار ورودی با مجموعه داده را محاسبه میکنیم:
def GetNeighbors(self,
x:np.ndarray) -> tuple:
d = x - self.trX
حال باید با استفاده از تابع numpy.linalg.norm فاصله دادهها را محاسبه میکنیم:
def GetNeighbors(self,
x:np.ndarray) -> tuple:
d = x - self.trX
Ds = np.linalg.norm(d, ord=self.p, axis=1)
با توجه به اینکه ماتریس d دارای 2 بعد است، میتوانیم در هر دو بعد Norm را محاسبه کنیم که در این مورد axis=1 صحیح است. نکته مهم دیگری که باید در نظر گرفت، ord=self.p است. این ورودی نقش مرتبه فاصله مینکوسکی را بر عهده دارد.
حال باید دادهها را با توجه به فاصله مرتب کنیم. به ان منظور تابع numpy.argsort مناسب است:
def GetNeighbors(self,
x:np.ndarray) -> tuple:
d = x - self.trX
Ds = np.linalg.norm(d, ord=self.p, axis=1)
Is = np.argsort(Ds)
با توجه به اینکه اولین عضو آرایه $$Is$$ مربوط به نزدیکترین همسایه است و ترتیب به شکل صعودی است، K مورد اول به عنوان همسایه انتخاب خواهد شد:
def GetNeighbors(self,
x:np.ndarray) -> tuple:
d = x - self.trX
Ds = np.linalg.norm(d, ord=self.p, axis=1)
Is = np.argsort(Ds)
iNs = Is[:self.K]
حال میتوانیم فاصله و مقدار ویژگی هدف $$K$$ همسایه نزدیک را استخراج کنیم و در خروجی برگردانیم:
def GetNeighbors(self,
x:np.ndarray) -> tuple:
d = x - self.trX
Ds = np.linalg.norm(d, ord=self.p, axis=1)
Is = np.argsort(Ds)
iNs = Is[:self.K]
dNs = Ds[iNs]
yNs = self.trY[iNs, 0]
return dNs, yNs
به این ترتیب این متد کامل شده و آماده استفاده است.
متد محاسبه وزنها برای پیاده سازی الگوریتم K نزدیکترین همسایه
این متد نیز در محاسبات متد Predict استفاده شد. در ورودی آرایه مربوط به فواصل K نزدیکترین همسایه را دریافت خواهیم کرد و در خروجی آرایه وزن را برمیگردانیم
def GetWeights(self,
dNs:np.ndarray) -> np.ndarray:
اگر مقدار self.W برابر با uniform باشد، تمامی وزنها با یکدیگر برابر بوده و برابر با $$1/k$$ خواهد بود:
def GetWeights(self,
dNs:np.ndarray) -> np.ndarray:
if self.W == 'uniform':
w = np.ones(self.K) / self.K
توجه داشته باشید که تابع numpy.ones در خروجی یک آرایه با ابعاد مشخص شده برمیگرداند که تمامی اعضای آن برابر با 1 است. بنابراین تقسیم کردن آن بر self.K وزنهای مورد نظر ما را ایجاد خواهد کرد.
در صورتی که شیوه وزندهی distance باشد، مسیر دیگری را در پیش خواهیم گرفت:
def GetWeights(self,
dNs:np.ndarray) -> np.ndarray:
if self.W == 'uniform':
w = np.ones(self.K) / self.K
elif self.W == 'distance':
در این حالت، دو اتفاق ممکن است رخ دهد:
- در مجموعه داده آموزش، دادهای وجود داشته باشد که به میزان بسیار زیادی به داده ورودی نزدیک باشد. در این شرایط مقدار فاصله بسیار کوچک خواهد شد و ممکن است برنامه با خطا مواجه شود.
- حالت اول رخ نمیدهد و نزدیکترین همسایه نیز دارای فاصله نسبتاً زیادی از داده ورودی است.
در حالت اول، وزنها را با عکس فاصله تعیین میکنیم و در نهایت آرایه حاصل را بر مجموع خود تقسیم میکنیم:
def GetWeights(self,
dNs:np.ndarray) -> np.ndarray:
if self.W == 'uniform':
w = np.ones(self.K) / self.K
elif self.W == 'distance':
if dNs[0] > 1e-6:
w = 1 / dNs
w = w / w.sum()
توجه داشته باشید که باید مجموع وزنها برابر با 1 باشد، بنابراین تقسیم آرایه $$w$$ بر مجموع خود ضروری است.
در صورتی که حالت اول رخ دهد (نزدیکترین همسایه دارای فاصلهای کمتر از $$1times 10^{-6}$$ باشد)، به همسایه اول وزن 1 میدهیم و وزن سایر همسایگان را برابر با 0 در نظر میگیریم:
def GetWeights(self,
dNs:np.ndarray) -> np.ndarray:
if self.W == 'uniform':
w = np.ones(self.K) / self.K
elif self.W == 'distance':
if dNs[0] > 1e-6:
w = 1 / dNs
w = w / w.sum()
else:
w = np.zeros(self.K)
w[0] = 1
return w
توجه داشته باشید که اگر همسایهای تا به این اندازه به بردار ورودی نزدیک باشد، میتوان با اطمینان بالایی گفت که شباهت کامل به یکدیگر دارند. تعیین مقدار $$1times 10^{-6}$$ باید با توجه به مقیاس دادهها انجام شود.
به این ترتیب تمامی موارد مورد نیاز برای آموزش مدل و پیشبینی ورودیهای جدید ایجاد شد.
دو متد دیگر نیز با نامهای RegressionReport و RegressionPlot نیز ایجاد میکنیم تا در نهایت بتوانیم به کمک آنها نتایج را ارزیابی کنیم.
گزارش رگرسیون
متدی با نام RegressionReport ایجاد میکنیم تا معیارهای ارزیابی را محاسبه و نمایش دهد. برای آشنایی با معیارهای ارزیابی رگرسیون، میتوانید به مطلب بررسی معیارهای ارزیابی رگرسیون در پایتون – پیادهسازی + کدها مراجعه کنید.
این متد در ورودی دو آرایه $$X$$، $$Y$$ و نام مجموعه داده ورودی را دریافت میکند:
ابتدا Range ویژگی هدف را محاسبه میکنیم:
def RegressionReport(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
Range = Y.max() - Y.min()
حال پیشبینی مدل را دریافت میکنیم و آرایه خطا (Error) را محاسبه میکنیم:
def RegressionReport(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
Range = Y.max() - Y.min()
P = self.Predict(X)
E = np.subtract(Y, P)
توجه داشته باشید که برای محاسبه اختلاف اعضای دو آرایه Numpy هم میتواند از عملگر – استفاده کرد و هم از تابع numpy.subtract استفاده کرد.
حال میتوانیم میانگین مربعات خطا (Mean Squared Error یا MSE) را با استفاده از تابع numpy.power و متد mean محاسبه کرد:
def RegressionReport(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
Range = Y.max() - Y.min()
P = self.Predict(X)
E = np.subtract(Y, P)
MSE = np.power(E, 2).mean()
توجه داشته باشید که میتوان از عملگر ** نیز برای به توان رساندن خطاها استفاده کرد.
حال میتوانیم ریشه دوم MSE را محاسبه کنیم و به این ترتیب مقدار RMSE یا Root Mean Squared Error حاصل خواهد شد:
def RegressionReport(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
Range = Y.max() - Y.min()
P = self.Predict(X)
E = np.subtract(Y, P)
MSE = np.power(E, 2).mean()
RMSE = MSE ** 0.5
حال میتوان NRMSE یا Normalized Root Mean Squared Error را نیز محاسبه کرد. به این منظور، مقدار RMSE را بر Range تقسیم میکنیم:
def RegressionReport(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
Range = Y.max() - Y.min()
P = self.Predict(X)
E = np.subtract(Y, P)
MSE = np.power(E, 2).mean()
RMSE = MSE ** 0.5
NRMSE = 100 * RMSE / Range
با توجه به اینکه NRMSE بدون واحد است، میتوان آن را به درصد بیان کرد.
حال میانگین قدرمطلق خطا (MAE یا Mean Absolute Error) را نیز محاسبه میکنیم:
def RegressionReport(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
Range = Y.max() - Y.min()
P = self.Predict(X)
E = np.subtract(Y, P)
MSE = np.power(E, 2).mean()
RMSE = MSE ** 0.5
NRMSE = 100 * RMSE / Range
MAE = np.abs(E).mean()
حال میتوانیم NMAE یا Normalized Mean Absolute Error را نیز محاسبه کنیم. به این منظور مقدار MAE را بر Range تقسیم میکنیم:
def RegressionReport(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
Range = Y.max() - Y.min()
P = self.Predict(X)
E = np.subtract(Y, P)
MSE = np.power(E, 2).mean()
RMSE = MSE ** 0.5
NRMSE = 100 * RMSE / Range
MAE = np.abs(E).mean()
NMAE = 100 * MAE / Range
این معیار نیز بدون واحد است بنابراین میتواند به درصد بیان شود.
معیار بعدی که باید محاسبه کنیم، میانگین قدرمطلق درصد خطا (MAPE یا Mean Absolute Percentage Error) است. برای محاسبه این معیار ابتدا مقادیر خطا را بر مقدار واقعی تقسیم میکنیم. خروجی این محاسبه، آرایه مربوط به خطاهای نسبی خواهد بود. با میانگینگیری از این آرایه و ضرب آن در 100، به مقدار مورد نظر میرسیم:
def RegressionReport(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
Range = Y.max() - Y.min()
P = self.Predict(X)
E = np.subtract(Y, P)
MSE = np.power(E, 2).mean()
RMSE = MSE ** 0.5
NRMSE = 100 * RMSE / Range
MAE = np.abs(E).mean()
NMAE = 100 * MAE / Range
MAPE = 100 * np.abs(E / Y).mean()
حال مهمترین معیار مورد بررسی در رگرسیون، یعنی $$R^{2}$$ را محاسبه میکنیم. براساس محاسبات میتوان اثبات کرد که این معیار به کمک MSE و واریانس مقادیر هدف قابل محاسبه هست. بنابراین خواهیم داشت:
def RegressionReport(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
Range = Y.max() - Y.min()
P = self.Predict(X)
E = np.subtract(Y, P)
MSE = np.power(E, 2).mean()
RMSE = MSE ** 0.5
NRMSE = 100 * RMSE / Range
MAE = np.abs(E).mean()
NMAE = 100 * MAE / Range
MAPE = 100 * np.abs(E / Y).mean()
R2 = 100 * (1 - MSE / np.var(Y))
در برخی موارد مقدار R نیز گزارش میشود که برای محاسبه آن باید از مقدار $$R^{2}$$ جذر بگیرید. اما با توجه به اینکه آن را به درصد محاسبه کردهایم، باید ابتدا تقسیم بر 100 شود، جذر گرفته شود و در نهایت دوباره ضرب در 100 شود. سادهسازی این فرآیند به فرمول زیر میانجامد:
def RegressionReport(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
Range = Y.max() - Y.min()
P = self.Predict(X)
E = np.subtract(Y, P)
MSE = np.power(E, 2).mean()
RMSE = MSE ** 0.5
NRMSE = 100 * RMSE / Range
MAE = np.abs(E).mean()
NMAE = 100 * MAE / Range
MAPE = 100 * np.abs(E / Y).mean()
R2 = 100 * (1 - MSE / np.var(Y))
R = 10 * R2 ** 0.5
به این ترتیب 8 معیار ارزیابی رگرسیون را پیادهسازی کردیم. حال میتوانیم آنها را در قالبی مشخص به کاربر نمایش دهیم:
def RegressionReport(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
Range = Y.max() - Y.min()
P = self.Predict(X)
E = np.subtract(Y, P)
MSE = np.power(E, 2).mean()
RMSE = MSE ** 0.5
NRMSE = 100 * RMSE / Range
MAE = np.abs(E).mean()
NMAE = 100 * MAE / Range
MAPE = 100 * np.abs(E / Y).mean()
R2 = 100 * (1 - MSE / np.var(Y))
R = 10 * R2 ** 0.5
print(f'KNN Regression Report For {Dataset} Dataset:')
print(f'MSE: {MSE:.4f}')
print(f'RMSE: {RMSE:.4f}')
print(f'NRMSE: {NRMSE:.2f} %')
print(f'MAE: {MAE:.4f}')
print(f'NMAE: {NMAE:.2f} %')
print(f'MAPE: {MAPE:.2f} %')
print(f'R2: {R2:.2f} %')
print(f'R: {R:.2f} %')
print('_' * 60)
به این ترتیب این متد قابلیت این را خواهد داشت که با گرفتن یک مجموعه داده، پیشبینی الگوریتم را دریافت کرده و تمامی معیارهای گفته شده را نمایش دهد. در صورت نیاز میتوان موارد محاسبه شده را در خروجی نیز برگرداند.
نمودار رگرسیون در پیاده سازی الگوریتم K نزدیکترین همسایه
معیارهای ارزیابی به عنوان یک عدد، یک برآورد از کل نتایج را توصیف میکنند. برای نمایش بهتر نتایج، میتوانیم از نمودارها استفاده کنیم. در این متد قصد داریم مقادیر پیشبینی را در مقابل مقادیر واقعی نمایش دهیم. در ورودی مجموعه داده و اسم مجموعه داده ورودی را دریافت میکنیم:
def RegressionPlot(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
حال پیشبینی مدل را دریافت میکنیم:
def RegressionPlot(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
P = self.Predict(X)
برای محاسبه نقاط ابتدا و انتهای نمودار، به شکل زیر دو عدد a و b را محاسبه میکنیم:
def RegressionPlot(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
P = self.Predict(X)
a = min(Y.min(), P.min())
b = max(Y.max(), P.max())
ab = np.array([a, b])
حال مقادیر P را در مقابل مقادیر Y رسم میکنیم:
def RegressionPlot(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
P = self.Predict(X)
a = min(Y.min(), P.min())
b = max(Y.max(), P.max())
ab = np.array([a, b])
plt.scatter(Y,
P,
s=20,
c='teal',
marker='s',
alpha=0.8,
label='Data')
3 خط نیز برای نمایش بهترین حالت و محدوده خطای 20 درصد رسم میکنیم:
def RegressionPlot(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
P = self.Predict(X)
a = min(Y.min(), P.min())
b = max(Y.max(), P.max())
ab = np.array([a, b])
plt.scatter(Y,
P,
s=20,
c='teal',
marker='s',
alpha=0.8,
label='Data')
plt.plot(ab,
ab,
ls='-',
lw=1.2,
c='k',
label='Y=X')
plt.plot(ab,
0.8 * ab,
ls='--',
lw=1,
c='r',
label='Y=0.8*X')
plt.plot(ab,
1.2 * ab,
ls='--',
lw=1,
c='r',
label='Y=1.2*X')
حال باید موضوع نمودار و اسم محورها را نیز اضافه کنیم و در نهایت نمودار را نشان دهیم:
def RegressionPlot(self,
X:np.ndarray,
Y:np.ndarray,
Dataset:str):
P = self.Predict(X)
a = min(Y.min(), P.min())
b = max(Y.max(), P.max())
ab = np.array([a, b])
plt.scatter(Y,
P,
s=20,
c='teal',
marker='s',
alpha=0.8,
label='Data')
plt.plot(ab,
ab,
ls='-',
lw=1.2,
c='k',
label='Y=X')
plt.plot(ab,
0.8 * ab,
ls='--',
lw=1,
c='r',
label='Y=0.8*X')
plt.plot(ab,
1.2 * ab,
ls='--',
lw=1,
c='r',
label='Y=1.2*X')
plt.title(f'KNN Regression Report For {Dataset} Dataset')
plt.xlabel('Target Values')
plt.ylabel('Predicted Values')
plt.legend()
plt.show()
به این ترتیب تمامی متدهای مورد نیاز برای کلاس KNNregression را پیادهسازی میکنیم.
تولید مجموعه داده برای پیاده سازی الگوریتم K نزدیکترین همسایه
در ابتدای کار، تنظیمات زیر را اعمال میکنیم:
np.random.seed(0)
plt.style.use('ggplot')
حال باید یک مجموعه داده تولید کنیم که بتوانیم بر روی آن الگوریتم را اعمال کنیم. به این منظور 1000 داده با 3 متغیر مستقل ورودی در نظر میگیریم:
nD = 1000
nX = 3
با توجه به اینکه باید بخشی از مجموعه داده نیز برای آزمایش (Test) مدل جدا شود، باید نسبت دادههای آموزش (Train Dataset) به کل را نیز تعیین کنیم:
sTr = 0.7حال میتوانیم آرایه $$X$$ را به صورت تصادفی در بازه $$[-1, +1]$$ ایجاد کنیم:
X = np.random.uniform(low=-1,
high=+1,
size=(nD, nX))
حال رابطه زیر را در نظر میگیریم:
$$
y=5+1.2 x_{1}-2 x_{2}^{2}+frac{4}{1+4 x_{3}^{2}}
$$
به این ترتیب ترکیبی از روابط خطی و غیرخطی را خواهیم داشت. به منظور محاسبه آرایه $$Y$$ به شکل زیر عمل میکنیم:
Y = 5 + 1.2*X[:, 0] - 2*X[:, 1]**2 + 4/(1+4*X[:, 2]**2)
Y = Y.reshape(-1, 1)
توجه داشته باشید که آرایه $$Y$$ باید به صورت عمودی باشد. حال میتوانیم Scatter Plot مربوط به هر کدام از ویژگیهای ورودی را با ویژگی هدف رسم کنیم:
for i in range(nX):
plt.scatter(X[:, i],
Y[:, 0],
s=20,
c='teal',
marker='o')
plt.title('Data Scatter Plot')
plt.xlabel(f'X{i + 1}')
plt.ylabel('Y')
plt.show()
پس از اجرای کد، سه نمودار زیر حاصل میشود:
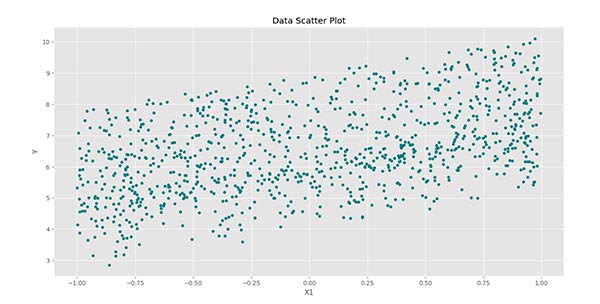
در این نمودار به خوبی میتوان ارتباط خطی بین $$Y$$ و $$X_1$$ را مشاهده کرد.
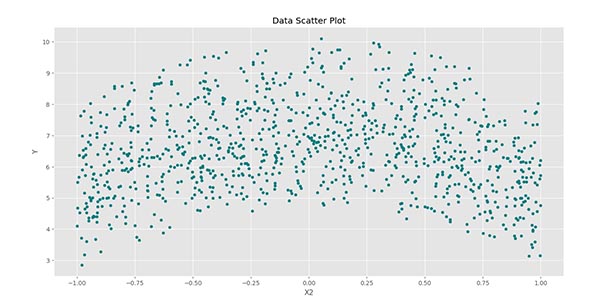
در این نمودار نیز یک ارتباط درجه دوم بین $$Y$$ و $$X_2$$ دیده میشود.
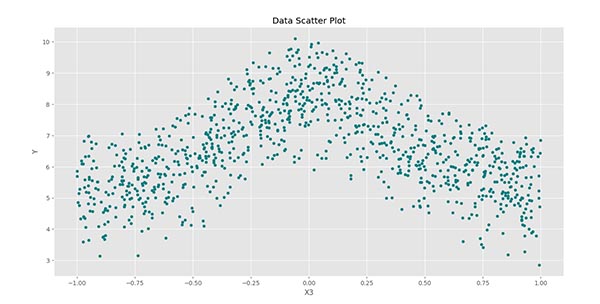
برای $$X_3$$ نیز نمودار فوق حاصل میشود. به این ترتیب در این حالت نیز ارتباطی غیرخطی وجود دارد.
تقسیم داده در پیاده سازی الگوریتم K نزدیکترین همسایه
حال تعداد دادههای آموزش را محاسبه میکنیم:
nDtr = round(sTr * nD)با توجه به اینکه حاصل عبارت داخل پارانتر اعشاری است، حتماً باید به یک عدد صحیح تبدیل شود.
حال دادهها را برش میدهیم تا تقسیم شوند:
trX = X[:nDtr]
teX = X[nDtr:]
trY = Y[:nDtr]
teY = Y[nDtr:]
ایجاد و آموزش مدل در پیاده سازی الگوریتم K نزدیکترین همسایه
با توجه به موارد گفته شده برای پیاده سازی الگوریتم K نزدیکترین همسایه حال میتوانیم مدل را ایجاد کنیم:
Model = KNNregression()برای آموزش مدل از متد Train استفاده میکنیم:
Model.Train(trX, trY)حال مدل آموزش دیده است و میتوانیم آن را ارزیابی کنیم. در اولین مرحله میتوانیم Regression Report را برای مجموعه داده آموزش و آزمایش بررسی کنیم:
Model.RegressionReport(trX, trY, 'Train')
Model.RegressionReport(teX, teY, 'Test')
در خروجی کد فوق، خروجیهای زیر حاصل خواهد شد:
KNN Regression Report For Train Dataset:
MSE: 0.0493
RMSE: 0.2221
NRMSE: 3.26 %
MAE: 0.1745
NMAE: 2.56 %
MAPE: 2.86 %
R2: 97.42 %
R: 98.70 %
به این ترتیب مشاهده میکنیم که مقدار $$R^{2}$$ برابر با 97٫42 درصد و بسیار مناسب است. برای مجموعه داده آزمایش، نتایج به شکل زیر خواهد بود:
KNN Regression Report For Test Dataset:
MSE: 0.0616
RMSE: 0.2481
NRMSE: 3.42 %
MAE: 0.1838
NMAE: 2.53 %
MAPE: 2.94 %
R2: 96.93 %
R: 98.45 %
برای مجموعه داده آزمایش مقدار $$R^{2}$$ برابر با 96٫93 درصد است که این مورد نیز مناسب است. بنابراین میتوان گفت که مدل بر روی مجموعه داده آموزش و آزمایش به نتایج خوبی رسیده است.
برای مصوسازی عملکرد مدل، میتوانیم Regression Plotها را رسم کنیم:
Model.RegressionPlot(trX, trY, 'Train')
Model.RegressionPlot(teX, teY, 'Test')
برای این کدها نیز نتایج به شکل زیر خواهد بود:

به این ترتیب مشاهده میکنیم که اغلب دادهها فاصله مناسبی از خط مشکی دارند. تمامی دادهها نیز در فاصله بین دو خط قرمز قرار دارند که نشان میدهد خطای بیشتر از 20 درصد نداریم.
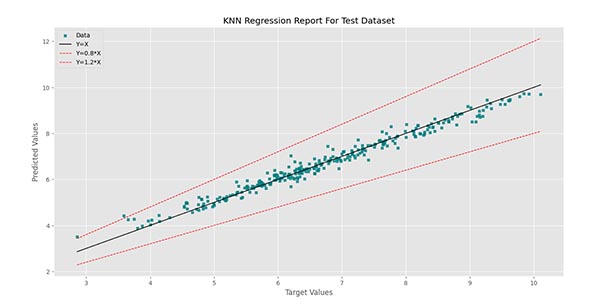
برای مجموعه داده آزمایش نمودار زیر را خواهیم داشت:
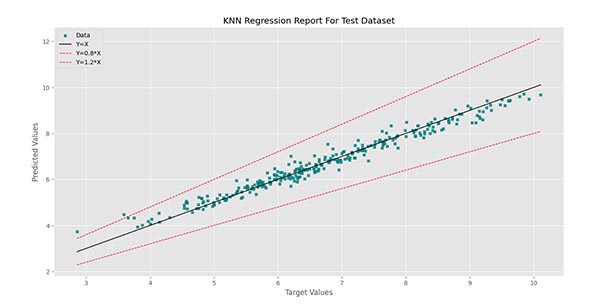
برای مجموعه داده آزمایش (Test Dataset) مشاهده میکنیم که به جز 2 داده، بقیه موارد بین دو خط قرمز قرار دارند. همچنان تمرکز اغلب دادهها بر روی خط مشکی است.
به این ترتیب با تنظیمات پیشفرض، توانستیم الگوریتم را ایجاد کنیم، آموزش دهیم و نتایج را ارزیابی کنیم.
میتوانیم برای وزندهی براساس فاصله نیز الگوریتم را ایجاد و آموزش دهیم:
Model = KNNregression(W='distance')
Model.Train(trX, trY)
در این شرایط، دو نمودار رگرسیون به شکل زیر خواهد بود:

به این ترتیب مشاهده میکنیم که مجموعه داده آموزش با دقت 100 درصد پیشبینی شده است. این اتفاق درحالی رخ میدهد که مجموعه داده آزمایش با دقت 97٫47 درصد پیشبینی میشود. این اتفاق به این دلیل رخ میدهد که مدل با دریافت یک داده آموزش، به عنوان اولین همسایه، خود آن داده را مییابد. با توجه به 0 بودن فاصله داده با خود، وزن آن به 1 تغییر مییابد، بنابراین مجموعه داده آموزش را بدون خطا پیشبینی میکند.
جمع بندی پیاده سازی الگوریتم K نزدیکترین همسایه
به این ترتیب پیادهسازی الگوریتم KNN برای رگرسیون به اتمام میرسد. برای مطالعه بیشتر، میتوان موارد زیر را بررسی کرد:
- به جز حالت گفته شده، در چه شرایطی الگوریتم برای مجموعه داده آموزش به دقت 100 درصد دست مییابد؟
- به جز فاصله مینوسکی، چه معیارهای دیگری برای سنجش فاصله وجود دارد؟
- با بررسی هایپرپارامترهای (Hyperparameter) مختلف، دقت الگوریتم بر روی مجموعه داده آزمایش را بیشینه کنید.
- اگر بخواهیم این الگوریتم را بدون استفاده از کتابخانه Numpy پیادهسازی کنیم، چه مشکلاتی وجود خواهد داشت؟
- ممکن است در هنگام استفاده، کاربر ورودیهای نادرست برای کلاس و متدهای آن تعریف کند. برای جلوگیری از این اتفاق، از assert استفاده میشود. کد نوشته شده را با استفاده از این دستور، تکمیل کنید.

