پیاده سازی الگوریتم ژنتیک در پایتون – راهنمای گام به گام

در این مطلب قصد داریم الگوریتم ژنتیک را در پایتون پیادهسازی کرده و از آن برای بیشینهسازی (Maximization) (که نوعی بهینهسازی (Optimization) است) یک تابع دلخواه استفاده کنیم. از مطالب پیشنیاز و مفید برای یادگیری این مطلب میتوان به «مولکول DNA چیست؟ – از صفر تا صد»، «ژن چیست؟ – به زبان ساده»، «الگوریتم ژنتیک – از صفر تا صد»، «میانگین متحرک چیست؟ + پیاده سازی Moving Average در پایتون» و «بررسی معیارهای ارزیابی رگرسیون در پایتون – پیاده سازی + کد» اشاره کرد.

الگوریتم ژنتیک چیست؟
الگوریتم ژنتیک (Genetic Algorithm یا GA) یک الگوریتم از خانواده الگوریتمهای تکاملی (Evolutionary Algorithms یا EA) است. این الگوریتم با الهام گرفتن از روند تکامل ژن برای افزایش شانس زیستن موجودات طراحی شده است. ویژگیهای فیزیکی موجودات توسط ماده ژنتیک که DNA (Deoxyribonucleic Acid) نام دارد تنظیم میشود. DNA شامل تعداد زیادی ژن (Gene) است که هرکدام کنترل یک فرآیند را بر عهده دارد. ژنها در طول زمان در نتیجه انتخاب طبیعی (Natural Selection) تغییر یافته و بهینه میشوند.
برای مثال اگر ژن A مسئول تولید زهر برای یک گونه مار باشد، روشن بودن آن به نفع موجود خواهد بود، بنابراین در طول زمان مارهایی با ژن A خاموش، از چرخه رقابت حذف خواهند شد. در این مطلب قصد داریم الگوریتم ژنتیک را پیادهسازی کرده و از آن برای بیشینهسازی (Maximization) (که نوعی بهینهسازی (Optimization) است) یک تابع دلخواه استفاده کنیم. فرض کنید که تابعی به شکل زیر داریم که در ورودی یک بردار x به طول n دریافت کرده و در خروجی یک عدد برمیگرداند:
$$
f(x)=sum_{i=1}^n e^{-x_i^2}=e^{-x_1{ }^2}+e^{-x_2{ }^2}+cdots+e^{-x_n^2}
$$
میدانیم که این تابع از تعداد زیادی تابع گوسی تشکیل شده است. هر جزء مستقل از یکدیگر است و در نقطه x_i=0 به بیشترین مقدار ممکن خود میرسد. بنابراین اگر تمامی درایههای آرایه (Array) x برابر با 0 باشد، این تابع بیشینه خواهد بود و مقدار بیشینه برابر با n خواهد بود.
به این ترتیب یک تابعی خواهیم داشت که جواب نهایی و مقدار بیشینه آن را میدانیم. از این تابع میتوانیم برای بررسی عملکرد الگوریتم پیادهسازی شده استفاده کنیم. در طبیعت، موجودات با برازندگی (Fitness) بیشتر، احتمال بقای بیشتری دارند. از این تابع به عنوان تابع برازندگی (Fitness Function) استفاده خواهیم کرد.
پیادهسازی الگوریتم ژنتیک در پایتون
برای پیادهسازی الگوریتم ژنتیک در پایتون، در ابتدا کتابخانههای مورد نیاز را فراخوانی میکنیم:
import numpy as np
import typing as typ
import matplotlib.pyplot as pltاین 3 کتابخانه به ترتیب برای موارد زیر استفاده خواهند شد:
- کتابخانه Numpy
به دلیل تسهیل کار با آرایه، ماتریس و تولید اعداد تصادفی، به عنوان کتابخانه اصلی پیادهسازی استفاده خواهد شد.
- ماژول Typing
برای تعریف جنس ورودی توابع کاربرد دارد. این مورد لزومی نیست اما در استفاده از آن خوانایی کد را بالا میبرد.
- کتابخانه Matplotlib
برای رسم نمودار نتایج الگوریتم استفاده خواهد شد. مصورسازی (Visualization) نتایج الگوریتم، برای نمایش عملکرد آن و حتی دریافتن مشکلات آن الزامی است.
با توجه به اینکه از کلاسها (Class) و برنامهنویسی شیگرا (Object Oriented Programming یا OOP) برای پیادهسازی الگوریتم استفاده خواهیم کرد، ممکن است در فرآیند انتقال کدها خطایی صورت گیرد، به همین دلیل کدهای نهایی از این لینک در دسترس است.
- برای دانلود کدهای نهایی پیادهسازی الگوریتم ژنتیک در پایتون، + اینجا کلیک کنید.
در اولین مرحله، دو تنظیمات زیر را اعمال میکنیم:
np.random.seed(0)
plt.style.use('ggplot')در طول کار الگوریتم ژنتیک در پایتون، از اعداد تصادفی (Random Number) استفاده میشود. در صورتی که سطر اول کد اعمال نشود، در هر بار اجرای کد نتایج متفاوتی خواهیم گرفت. در صورتی که قصد تنظیم برخی پارامترهای الگوریتم را داشته باشیم، این اتفاق مناسب نیست. سطر دوم برای زیباتر کردن ظاهر نمودارها استفاده میشود.
پیادهسازی الگوریتم
برای پیادهسازی الگوریتم ژنتیک در پایتون، در اولین قدم، یک کلاس با نام GA ایجاد میکنیم:
class GA:پیادهسازی متد سازنده
برای کامل شدن این کلاس، به 8 متد (Method) نیاز داریم. به عنوان اولین متد، متد سازنده را ایجاد میکنیم که با نام __init__
میشناسیم. این متد در ورودی 6 عدد دریافت میکند که تنظیمات کار الگوریتم است:
def __init__(self,
MaxGeneration:int=100,
PopulationSize:int=100,
MatingFraction:float=0.1,
MutationFraction:int=0.2,
MutationProbability:float=0.1,
MutationScale:float=0.04):6 ورودی به ترتیب موارد زیر را تنظیم میکنند:
- ورودی MaxGeneration
بیشترین تعداد نسلها را نشان میدهد. افزایش تعداد نسلها، احتمال بهینهتر شدن بهترین عضو جمعیت را افزایش میدهد. افزایش MaxGeneration زمان اجرای الگوریتم و تعداد دفعات فراخوانی تابع هدف (Function Evaluation) را نیز افزایش میدهد. در طبیعت نیز با گذر زمان، در نسلهای جدیدتر، کروموزومهای (Chromosome) برازندهتر ایجاد میشود. این ورودی به مقدار پیشفرض 100 نسل تنظیم شده است.
- ورودی PopulationSize
اندازه جمعیت را نشان میدهد. در هر مرحله از کار الگوریتم، تعداد مشخصی از بهترین کروموزومها انتخاب و به نسل بعد منتقل میشود. با توجه به روش پیادهسازی الگوریتم، با افزایش این عدد نیز زمان اجرای الگوریتم افزایش خواهد داشت. در طبیعت نیز به دلیل محدود بودن منابع (Resource)، ظرفیت ادامه حیات برای تعداد محدودی از موجودات یک گونه وجود دارد. این ورودی به مقدار پیشفرض 100 کروموزوم تنظیم شده است.
- ورودی MatingFraction
کسر (Fraction) مربوط به تعداد آمیزش (Mating) در هر نسل را نشان میدهد. این عدد بهتر است در بازه [0,1] باشد. برای مثال اگر این عدد برابر با 0.2 باشد و اندازه جمعیت 80 باشد، در هر نسل به تعداد 0.2×80=16 آمیزش صورت خواهد گرفت و 32 فرزند حاصل خواهد شد. بنابراین، افزایش این عدد باعث افزایش زمان اجرای الگوریتم ژنتیک در پایتون میشود. این ورودی به مقدار پیشفرض 0.1 تنظیم شده است.
- ورودی MutationFraction
مشابه ورودی قبل، تعداد جهش (Mutation) در هر نسل را تنظیم میکند. با افزایش این ورودی نیز زمان اجرای الگوریتم افزایش خواهد یافت. این ورودی به مقدار پیشفرض 0.2 تنظیم شده است.
- ورودی MutationProbability
احتمال جهش در ژنها را تعیین میکند. برای مثال اگر مقدار این ورودی 0.5 تعیین شود و از جمعیت موجود، یک کروموزوم انتخاب شود و شامل 40 ژن باشد، هر ژن با احتمال 50% خواهد توانست جهش کند. کم بودن این ورودی باعث میشود الگوریتم نتواند به خوبی حول جوابهای بهینه موجود تا آن نسل جستجو کند. زیاد بودن این ورودی باعث میشود احتمال بهبود برازندگی در کروموزوم جهشیافته کاهش یابد. به همین دلیل بهتر است مقدار آن در حد بهینه حفظ شود. مقدار این ورودی به مقدار پیشفرض 0.1 تنظیم شده است.
- ورودی MutationScale
حدود بزرگی (Scale) جهش را تعیین میکند. برای مثال اگر حدود ژن K بازه [-2,+6] باشد، در صورتی که MutationScale
برابر با 0.2 باشد، بیشترین بزرگی ممکن برای جهش آن ژن برابر خواهد بود با:
$$
0.2×(+6-(-2))=0.2×(+6+2)=0.2×8=1.6
$$
نصف این تغییرات برای افزایش و نصف دیگر آن برای کاهش خواهد بود. در این صورت میزان جهش برای ژن K در بازه [-0.8,+0.8] خواهد بود. برای جهش یک عدد از این بازه انتخاب و به مقدار قبلی ژن اضافه میشود. این ورودی باید در بازه [0,2] باشد، اما مقادیر نزدیک به صفر مناسب است.
مقادیر بالای این ورودی در نسلهای ابتدایی ممکن است مناسب باشد اما در نسلهای انتهای چندان مناسب نخواهد بود. مقدار این ورودی به مقدار پیشفرض 0.04 تنظیم شده است. پس از دریافت این مقادیر، آنها را در شی (Object) که با نام self
میشناسیم ذخیره میکنیم. به این ترتیب شش Attribute به شی اضافه خواهد شد:
def __init__(self,
MaxGeneration:int=100,
PopulationSize:int=100,
MatingFraction:float=0.1,
MutationFraction:int=0.2,
MutationProbability:float=0.1,
MutationScale:float=0.04):
self.MaxGeneration = MaxGeneration
self.PopulationSize = PopulationSize
self.MatingFraction = MatingFraction
self.MutationFraction = MutationFraction
self.MutationProbability = MutationProbability
self.MutationScale = MutationScaleحال نیاز است دو عدد دیگر نیز محاسبه کنیم. در ابتدا باید عددی به نام MatingCount
را حساب کنیم. این عدد تعداد آمیزش در هر نسل را نشان خواهد داد. به این منظور باید اندازه جمعیت در کسر آمیزش ضرب شود:
def __init__(self,
MaxGeneration:int=100,
PopulationSize:int=100,
MatingFraction:float=0.1,
MutationFraction:int=0.2,
MutationProbability:float=0.1,
MutationScale:float=0.04):
self.MaxGeneration = MaxGeneration
self.PopulationSize = PopulationSize
self.MatingFraction = MatingFraction
self.MutationFraction = MutationFraction
self.MutationProbability = MutationProbability
self.MutationScale = MutationScale
self.MatingCount = round(PopulationSize * MatingFraction)توجه داشته باشید که عدد حاصل از نوع اعشاری (Float) است، به همین دلیل از تابع Round
برای گرد کردن آن به نزدیکترین عدد صحیح (Integer) استفاده میکنیم. این فرآیند را برای محاسبه تعداد جهش در هر نسل هم استفاده میکنیم:
def __init__(self,
MaxGeneration:int=100,
PopulationSize:int=100,
MatingFraction:float=0.1,
MutationFraction:int=0.2,
MutationProbability:float=0.1,
MutationScale:float=0.04):
self.MaxGeneration = MaxGeneration
self.PopulationSize = PopulationSize
self.MatingFraction = MatingFraction
self.MutationFraction = MutationFraction
self.MutationProbability = MutationProbability
self.MutationScale = MutationScale
self.MatingCount = round(PopulationSize * MatingFraction)
self.MutationCount = round(PopulationSize * MutationFraction)نتایج الگوریتم ژنتیک در پایتون باید در طول آموزش ذخیره شود. به همین منظور یک دیکشنری (Dictionary) به شکل زیر ایجاد میکنیم تا در ادامه کار الگوریتم نتایج در آن ذخیره شود:
def __init__(self,
MaxGeneration:int=100,
PopulationSize:int=100,
MatingFraction:float=0.1,
MutationFraction:int=0.2,
MutationProbability:float=0.1,
MutationScale:float=0.04):
self.MaxGeneration = MaxGeneration
self.PopulationSize = PopulationSize
self.MatingFraction = MatingFraction
self.MutationFraction = MutationFraction
self.MutationProbability = MutationProbability
self.MutationScale = MutationScale
self.MatingCount = round(PopulationSize * MatingFraction)
self.MutationCount = round(PopulationSize * MutationFraction)
self.History = {'Best': [],
'Best F': [],
'Worst F': [],
'Average F': [],
'FEs': []}لیست (List) مربوط به کلید Best
بهترین کروموزوم هر نسل را ذخیره خواهد کرد. بیشترین، کمترین و میانگین برازندگی کروموزومهای هر نسل نیز به ترتیب در لیست مربوط به کلیدهای Best F
، Worst F
و Average F
ذخیره خواهد شد. به این ترتیب خواهیم توانست روند بهبود نتایج الگوریتم را در نهایت با یک نمودار نشان دهیم. لیست مربوط به کلید FEs نیز مقدار تابع برازندگی در هر بار فراخوانی آن را ذخیره خواهد کرد. به این ترتیب متد __init__
کامل میشود.
پیادهسازی متد محاسبه برازش
متد بعدی که باید پیادهسازی شود، مربوط به محاسبه تابع برازندگی است. این تابع با دریافت یک مجموعه از کروموزومها (جمعیت یا Population)، برازندگی هر کروموزوم را محاسبه و در خروجی برخواهد گرداند. یک متد با نام GetFitnessees
ایجاد میکنیم و در ورودی تابع، آرایه مربوط به جمعیت را دریافت میکنیم:
def GetFitnesses(self,
Population:np.ndarray) -> np.ndarray:حال به ازای هر کروموزوم در جمعیت، تابع برازندگی را فراخوانی میکنیم، خروجی را در یک لیست ذخیره و در نهایت با استفاده از تابع numpy.array
آن را به آرایه تبدیل میکنیم:
def GetFitnesses(self,
Population:np.ndarray) -> np.ndarray:
Fitnesses = np.array([self.F(i) for i in Population])توجه داشته باشید که برخی توابع، به جز متغیرهای تصمیم (Decision Variable)، ورودیهای دیگری نیز دریافت میکنند، به همین دلیل یک Attribute به نام Args
نیز در شی ایجاد خواهیم کرد و در ورودی تابع وارد خواهیم کرد:
def GetFitnesses(self,
Population:np.ndarray) -> np.ndarray:
Fitnesses = np.array([self.F(i, *self.Args) for i in Population])به این ترتیب الگوریتم نوشته شده توانایی بهینهسازی توابع متنوعی را خواهد داشت. میتوان یک Attribute به عنوان self.kwArgs
نیز اضافه کنیم که فعلاً از آن صرف نظر میکنیم. قبل از اینکه آرایه Fitnesses
در خروجی برگردانده شود، مقادیر آن را به لیست کلید FEs
در دیکشنری self.History
اضافه میکنیم:
def GetFitnesses(self,
Population:np.ndarray) -> np.ndarray:
Fitnesses = np.array([self.F(i, *self.Args) for i in Population])
self.History['FEs'].extend(Fitnesses)در نهایت آرایه برازندگیهای محاسبه شده را به عنوان خروجی برمیگردانیم:
def GetFitnesses(self,
Population:np.ndarray) -> np.ndarray:
Fitnesses = np.array([self.F(i, *self.Args) for i in Population])
self.History['FEs'].extend(Fitnesses)
return Fitnessesبه این ترتیب متد GetFitnesses
کامل میشود.
پیادهسازی متد مرتبسازی جمعیت
در مراحل مختلف کار الگوریتم ژنتیک در پایتون، نیاز خواهیم داشت که جمعیت را مرتب کنیم، با توجه به اینکه فرآیندهای آمیزش و جهش کروموزومهای جدیدی تولید میکند، باید بهترین کروموزومهای جمعیت پس از مرتبسازی آنها انتخاب شود. متدی با نام Sort
ایجاد میکنیم. این تابع ورودی به خصوصی نخواهد داشت و موارد مورد نیاز را از شی دریافت کرده، آنها پردازش کرده و در شی ذخیره خواهد کرد. در ابتدا با استفاده از تابع numpy.argsort
ترتیب کروموزومها را محاسبه میکنیم:
def Sort(self):
I = np.argsort(self.Fitnesses)خروجی حاصل، به شکل صعودی خواهد بود، در صورتی که نیاز داریم تا بهترین کروموزومها در ابتدای آرایه قرار گیرند و روند نزولی باشد، به همین دلیل آن را با استفاده از تابع numpy.flip
برعکس میکنیم:
def Sort(self):
I = np.argsort(self.Fitnesses)
I = np.flip(I)حال دو آرایه self.Population
و self.Fitnesses
را به کمک آرایه I
مرتب میکنیم:
def Sort(self):
I = np.argsort(self.Fitnesses)
I = np.flip(I)
self.Population = self.Population[I]
self.Fitnesses = self.Fitnesses[I]به این ترتیب، هربار که کد self.Sort()
اجرا شود، آرایه self.Fitnesses
به صورت نزولی مرتب شده و آرایه self.Population
با توجه به ترتیب self.Fitnesses
مرتب میشود. به این ترتیب متد Sort
کامل میشود.
پیادهسازی متد تولید کروموزومهای جهش یافته
متدی نیاز داریم تا در صورت فراخوانی، با توجه به تعداد تعریف شده، از جمعیت موجود کروموزوم جهشیافته (Mutants) تولید کند. متدی با نام GetMutants
ایجاد میکنیم. این متد در ورودی چیز دریافت نمیکند ولی در خروجی آرایه مربوط به کروموزومهای جهشیافته را برمیگرداند:
def GetMutants(self) -> np.ndarray:در تولید کروموزومهای جهشیافته، تمایل داریم تا بیشتر از کروموزومهای برازندهتر استفاده کنیم، زیر احتمال تولید کروموزومهای بهتر زیاد است. به این دلیل، احتمال انتخاب هر کروموزوم برای جهش دادن آن را، با توجه به میزان برازندگی آن تعیین میکنیم. اگر میزان برازندگی تمامی اعضای جمعیت، در آرایه F موجود باشد، ابتدا آن را به شکل زیر در بازه بین [0,1] مقیاسبندی (Scaling) میکنیم:
$$
F _ i ^ { ‘ } = frac { F _ i – min (F)}{ max (F) – min (F)}
$$
سپس برای توزیع احتمال بین هر عضو، از رابطه زیر استفاده میکنیم:
$$
P _ i ^ { ‘ } = frac { F _ i ^ { ‘ } }{ sum _ { j = 1 } ^ { n } F _ j ^ { ‘ } } = frac { F _ i ^ { ‘ } }{ sum ( F ^ {‘} ) }
$$
به این ترتیب اعضای با برازندگی بیشتر، احتمال بیشتری برای انتخاب خواهند داشت، همچنین مجموعه این احتمالات برابر با 1 است. برای پیادهسازی روابط فوق، کد زیر را استفاده میکنیم:
def GetMutants(self) -> np.ndarray:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()حال میتوانیم با توجه به آرایه p و به کمک تابع numpy.random.choice
کروموزومهایی که میخواهیم جهش دهیم را انتخاب کنیم:
def GetMutants(self) -> np.ndarray:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount,
p=p)توجه داشته باشید که در برخی شرایط، واریانس بسیار کمی بین در برازندگی جمعیت ایجاد میشود، در این شرایط ممکن است محاسبات مربوط آرایه p
به مشکل بخورد، به همین دلیل کد فوق را تحت شرایطی اجرا میکنیم که حداقل مقداری از واریانس وجود داشته باشد و در غیر این صورت، انتخاب را با احتمالات یکسان انجام میدهیم:
def GetMutants(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount)به این ترتیب کروموزومهای مورد نظر انتخاب میشود. توجه داشته باشید که ورودی a مربوط به تابع numpy.random.choice
میتواند یک آرایه باشد و از داخل آن موارد انتخاب شود. در صورتی که به جای آرایه، یک عدد صحیح وارد کنیم، اعدادی در بازه [0,a) انتخاب میشود.
در این مورد چون قصد داریم تعدادی کروموزوم از کل جمعیت انتخاب کنیم، مقدار a را برابر با self.PopulatinSize
قرار میدهیم. تعدد موارد انتخاب نیز با ورودی size تعیین میشود که به تعداد self.MutationCount
کروموزوم انتخاب میکنیم. حال کروموزومهای انتخاب شده را انتخاب و با اسم newP
میشناسیم:
def GetMutants(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount)
newP = self.Population[I]در این مرحله، آرایه newP
دارای self.MutationCount
عدد سطر (کروموزوم) و self.DimensionCount
عدد ستون (ژن) خواهد بود. تعداد ژنها در فراخوانی متد Maximize تعیین خواهد شد. حال باید به ازای هر کروموزوم یک حلقه ایجاد کنیم:
def GetMutants(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount)
newP = self.Population[I]
for i in range(self.MutationCount):حال باید به ازای هر ژن نیز تصمیمگیری کنیم، به همین دلیل حلقه دیگری نیز ایجاد میکنیم:
def GetMutants(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount)
newP = self.Population[I]
for i in range(self.MutationCount):
for j in range(self.DimensionCount):حال یک عدد تصادفی در بازه [0,1] ایجاد میکنیم. در صورتی که این عدد بزرگتر از self.MutationProbability
باشد، برای ژن j جهشی رخ نخواهد داد، در غیر این صورت یک جهش رخ خواهد داد:
def GetMutants(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount)
newP = self.Population[I]
for i in range(self.MutationCount):
for j in range(self.DimensionCount):
if np.random.rand() توجه داشته باشید که numpy.random.rand
یک عدد تصادفی در بازه بین 0 و 1 برمیگرداند. حال اگر شرط برقرار شد، ژن j از کروموزوم i را جهش میدهیم. مقدار جهش به صورت تصادفی در بازه Scaleهای محاسبه شده رخ خواهد داد:
def GetMutants(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount)
newP = self.Population[I]
for i in range(self.MutationCount):
for j in range(self.DimensionCount):
if np.random.rand() توجه داشته باشید که آرایه self.MutationScales
تعریف نشده است، و در متد Maximize
مقدار آن را تعریف خواهیم کرد. در این آرایه به ازای هر ژن بیشترین شدت از جهش ذخیره شده است.
پس از اتمام جهشهای کروموزوم i باید بررسی کنیم تا ژنی از حد بالا (Upper Bound) و حد پایین (Lower Bound) خود خارج نشود. به این منظور چهار سطر کد نیاز داریم که در ابتدا Maskهایی برای تعیین ژنهای خارج از بازه تولید کند و سپس موارد مشکلدار را اصلاح کند:
def GetMutants(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount)
newP = self.Population[I]
for i in range(self.MutationCount):
for j in range(self.DimensionCount):
if np.random.rand() self.UB
Mask2 = newP[i] دو آرایه Mask1
و Mask2
طولی برابر با newP[i]
خواهند داشت و مقادیر آنها True و یا False خواهد بود. در نهایت در دو سطر آخر، ژنهایی که از حد بالا گذشتهاند را به حد بالای خود و ژنهایی که از حد پایین خود گذشتهاند را به حد پایین خود منتقل میکنیم. توجه داشته باشید که دو آرایه self.LB
و self.UB
به ترتیب حد پایین و بالای ژنها را تعیین میکند که در متد Maximize
به عنوان ورودیهای مسئله دریافت خواهیم کرد.
در انتهای این تابع، آرایه newP
را برمیگردانیم:
def GetMutants(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=self.MutationCount)
newP = self.Population[I]
for i in range(self.MutationCount):
for j in range(self.DimensionCount):
if np.random.rand() self.UB
Mask2 = newP[i] به این ترتیب پیادهسازی متد GetMutants
به اتمام میرسد.
پیادهسازی متد تولید کروموزومهای فرزند
در الگوریتم ژنتیک در پایتون نیاز داریم تا با تعریف دو کروموزوم والد، دو کروموزوم فرزند ایجاد کنیم. مشابه متد تولید کروموزومهای جهشیافته، یک متد با نام GetChilds
ایجاد میکنیم. این متد در ورودی مورد به خصوصی دریافت نمیکند و همانند متد قبلی یک آرایه برمیگرداند:
def GetChilds(self) -> np.ndarray:حال مشابه قبل، با توجه به برازندگی هر کروموزوم، والدین را انتخاب میکنیم:
def GetChilds(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount)توجه داشته باشید که به تعداد دو برابر آمیزشها، نیاز به والد داریم. در خروجی نیز به تعداد دو برابر آمیزشها فرزند خواهیم داشت. حال نصف کروموزومهای انتخاب شده را به عنوان والد اول و نصف دوم را به عنوان والد دوم انتخاب میکنیم:
def GetChilds(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount)
I1s = I[:self.MatingCount]
I2s = I[self.MatingCount:]به این ترتیب I1s
شماره مربوط به کروموزومهای والد اول و I2s
شماره مربوط به کروموزومهای والد دوم را نشان خواهد داد. حال برای ذخیره فرزندان، دو آرایه خالی ایجاد میکنیم:
def GetChilds(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount)
I1s = I[:self.MatingCount]
I2s = I[self.MatingCount:]
newP1 = np.zeros((self.MatingCount, self.DimensionCount))
newP2 = np.zeros((self.MatingCount, self.DimensionCount))توجه داشته باشید که به تعداد دو برابر آمیزشها فرزند و self.DimensionCount
ژن داریم. حال برای هر آمیزش یک حلقه ایجاد میکنیم:
def GetChilds(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount)
I1s = I[:self.MatingCount]
I2s = I[self.MatingCount:]
newP1 = np.zeros((self.MatingCount, self.DimensionCount))
newP2 = np.zeros((self.MatingCount, self.DimensionCount))
for i, (i1, i2) in enumerate(zip(I1s, I2s)):این حلقه، با i شماره آمیزش، با i1
شماره کروموزوم والد اول و با i2
شماره کروموزوم وارد دوم را تعیین خواهد کرد. حال به ازای هر ژن حلقه دیگری ایجاد میکنیم:
def GetChilds(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount)
I1s = I[:self.MatingCount]
I2s = I[self.MatingCount:]
newP1 = np.zeros((self.MatingCount, self.DimensionCount))
newP2 = np.zeros((self.MatingCount, self.DimensionCount))
for i, (i1, i2) in enumerate(zip(I1s, I2s)):
for j in range(self.DimensionCount):در این نقطه باید کراسینگ اور (Crossing Over) را پیادهسازی میکنیم. روشهای متنوعی برای انجام کراسینگ اور وجود دارد که در این حالت روش Uniform را استفاده خواهیم کرد.
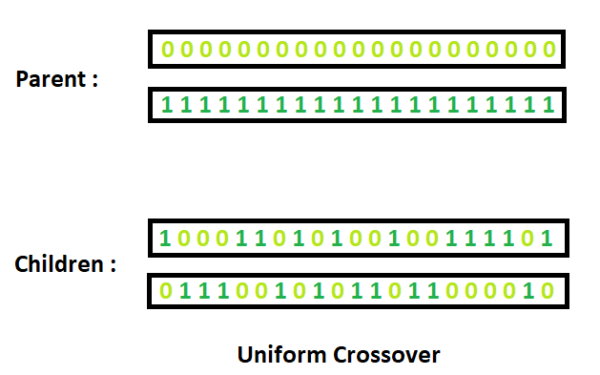
در این حالت برای هر ژن مستقل از سایرین تصمیم میگیریم. یک عدد تصادفی در بازه [0,1] ایجاد میکنیم. در صورتی که عدد حاصل کمتر از 0.5 باشد، فرزند اول آمیزش i ژن شماره j را از والد اول دریافت خواهد کرد. در صورتی که عکس این حالت رخ دهد، ژن j فرزند اول آمیزش i از والد دوم دریافت خواهد شد:
def GetChilds(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount)
I1s = I[:self.MatingCount]
I2s = I[self.MatingCount:]
newP1 = np.zeros((self.MatingCount, self.DimensionCount))
newP2 = np.zeros((self.MatingCount, self.DimensionCount))
for i, (i1, i2) in enumerate(zip(I1s, I2s)):
for j in range(self.DimensionCount):
if np.random.rand() به این ترتیب برای هر ژن j به صورت مستقل عمل کراسینگ اور رخ خواهد داد. در انتهای این حلقه، برای تمامی آمیزشها، دو فرزند حاصل خواهد شد. دو آرایه newP1
و newP2
باید به یکدیگر چسبانده شوند و در خروجی برگردانده شوند:
def GetChilds(self) -> np.ndarray:
if self.Fitnesses.var() > 1e-9:
p = (self.Fitnesses - self.Fitnesses.min()) / (self.Fitnesses.max() - self.Fitnesses.min())
p /= p.sum()
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount,
p=p)
else:
I = np.random.choice(a=self.PopulationSize,
size=2 * self.MatingCount)
I1s = I[:self.MatingCount]
I2s = I[self.MatingCount:]
newP1 = np.zeros((self.MatingCount, self.DimensionCount))
newP2 = np.zeros((self.MatingCount, self.DimensionCount))
for i, (i1, i2) in enumerate(zip(I1s, I2s)):
for j in range(self.DimensionCount):
if np.random.rand() به این ترتیب متد GetChilds
کامل میشود.
پیادهسازی متد افزودن جمعیت
در هر نسل از کار الگوریتم ژنتیک در پایتون، علاوه بر جمعیت فعلی، دو جمعیت از جهش و آمیزش حاصل میشود که باید اضافه شوند. به این ترتیب نیاز داریم متدی با اسم Append
ایجاد شود و در ورودی لیست جمعیتهای جدید را دریافت کنید:
def Append(self,
Ps:list):حال به ازای هر جمعیت، برازندگی آن را محاسبه و در لیستی ذخیره میکنیم:
def Append(self,
Ps:list):
Fs = [self.GetFitnesses(i) for i in Ps]حال نیاز داریم تا جمعیتهای موجود را به انتهای جمعیت قبلی اضافه و به عنوان self.Population
ذخیره کنیم:
def Append(self,
Ps:list):
Fs = [self.GetFitnesses(i) for i in Ps]
self.Population = np.vstack([self.Population] + Ps)در نهایت نیاز است تا برازندگی جمعیتهای جدید را نیز به انتهای آرایه self.Fitnesses
اضافه کرده و آن را بهروزرسانی کنیم:
def Append(self,
Ps:list):
Fs = [self.GetFitnesses(i) for i in Ps]
self.Population = np.vstack([self.Population] + Ps)
self.Fitnesses = np.hstack([self.Fitnesses] + Fs)به این ترتیب متد Append
کامل میشود.
پیادهسازی متد اصلاح اندازه جمعیت
پس از اضافه شدن جمعیت حاصل از جهش و آمیزش به جمعیت موجود، اندازه آن از self.PopulationSize
زیادتر میشود. نیاز است تا براساس انتخاب طبیعی، به تعداد مورد نیاز کروموزوم از بهترین موارد انتخاب و بقیه حذف شوند، به همین دلیل متدی با نام Cut
ایجاد میکنیم تا این عملیات را انجام دهد:
def Cut(self):
self.Population = self.Population[:self.PopulationSize]
self.Fitnesses = self.Fitnesses[:self.PopulationSize]توجه داشته باشید که باید قبل از فراخوانی این متد، متد Sort
فراخوانی شود تا کروموزومها به ترتیب نزولی مرتب شوند. به این ترتیب متد Cut کامل میشود و در صورتی که به شکل self.Cut()
فراخوانی شود، اندازه جمعیت را اصلاح خواهد کرد.
پیادهسازی متد بیشینهسازی
تا به ایجاد 7 متد مورد نیاز برای کار الگوریتم پیادهسازی شد. حال نیاز داریم تا متد نهایی که هسته اصلی کار الگوریتم است را پیادهسازی کنیم. این متد با نام Maximize
شناخته خواهد شد و در ورودی تابع برازندگی، حد پایین متغیرهای تصمیم، حد بالای متغیرهای تصمیم و سایر آرگومانهای ورودی تابع برازندگی را دریافت خواهد کرد. در خروجی این متد، یک دیکشنری که حاوی تاریخچه و نتایج الگوریتم است را برخواهیمگرداند:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:در ابتدای متد، موارد ورودی را ذخیره میکنیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Argsحال تعداد متغیرهای تصمیم، یا به عبارتی تعداد ژنها را محاسبه میکنیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Args
self.DimensionCount = LB.sizeهمانطور که در پیادهسازیها دیدیم، این عدد در عملیات سایر متدها استفاده میشود. حال نیاز داریم تا بیشترین بزرگی جهش برای هر ژن را محاسبه کنیم. به این منظور رابطه زیر را تعریف میکنیم:
$$
S _ i = S _ 0 times frac { U B _ i – L B _ i }{ 2 }
$$
در این رابطه، i شماره ژن، $$ S _ 0 $$ ورودی MutationScale
الگوریتم و LB
و UB
به ترتیب حد پایین و حد بالای متغیرهای تصمیم است. در متد GetMutants
اعداد تصادفی در بازه $$ [-S _ i , + S _ i] $$ انتخاب شدند، به همین دلیل به مخرج رابطه فوق عدد 2 اضافه شده است. حال نیاز داریم تا یک جمعیت اولیه ایجاد کنیم. به این منظور از numpy.random.uniform
استفاده میکنیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Args
self.DimensionCount = LB.size
self.MutationScales = self.MutationScale * (self.UB - self.LB) / 2
self.Population = np.random.uniform(low=self.LB,
high=self.UB,
size=(self.PopulationSize,
self.DimensionCount))حال برای جمعیت ایجاد شده، مقادیر برازندگی را محاسبه و به عنوان self.Fitnesses
ذخیره میکنیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Args
self.DimensionCount = LB.size
self.MutationScales = self.MutationScale * (self.UB - self.LB) / 2
self.Population = np.random.uniform(low=self.LB,
high=self.UB,
size=(self.PopulationSize,
self.DimensionCount))
self.Fitnesses = self.GetFitnesses(self.Population)به این ترتیب self.Population
و self.Fitnesses
مقداردهی اولیه (Initialization) میشوند. حال جمعیت را به صورت نزولی مرتب میکنیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Args
self.DimensionCount = LB.size
self.MutationScales = self.MutationScale * (self.UB - self.LB) / 2
self.Population = np.random.uniform(low=self.LB,
high=self.UB,
size=(self.PopulationSize,
self.DimensionCount))
self.Fitnesses = self.GetFitnesses(self.Population)
self.Sort()به این ترتیب مرحله 0 به اتمام رسیده است. نتایج این مرحله را ذخیره و در خروجی بیشترین برازندگی حاصل تا آن مرحله را نمایش میدهیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Args
self.DimensionCount = LB.size
self.MutationScales = self.MutationScale * (self.UB - self.LB) / 2
self.Population = np.random.uniform(low=self.LB,
high=self.UB,
size=(self.PopulationSize,
self.DimensionCount))
self.Fitnesses = self.GetFitnesses(self.Population)
self.Sort()
self.History['Best'].append(self.Population[0])
self.History['Best F'].append(self.Fitnesses[0])
self.History['Worst F'].append(self.Fitnesses[-1])
self.History['Average F'].append(self.Fitnesses.mean())
print('Generation 0 Best: {:.2f}'.format(self.Fitnesses[0]))توجه داشته باشید که پس از مرتبسازی، اولین عضو self.Population
بهترین جواب حاصل تا آن مرحله، اولین عضو self.Fitnesses
بیشترین برازندگی حاصل تا آن مرحله و آخرین عضو آن کمترین برازندگی موجد در آن مرحله است. به عنوان معیاری از کل جمعیت نیز میانگین برازندگی جمعیت به عنوان Average F
در نظر گرفته شده است. با توجه به اینکه self.Fitnesses
یک آرایه Numpy
است، میتوانیم از متد mean
برای محاسبه میانگین آرایه استفاده کرد. پس از اتمام مرحله مقداردهی اولیه، یک حلقه به طول self.MaxGeneration
ایجاد میکنیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Args
self.DimensionCount = LB.size
self.MutationScales = self.MutationScale * (self.UB - self.LB) / 2
self.Population = np.random.uniform(low=self.LB,
high=self.UB,
size=(self.PopulationSize,
self.DimensionCount))
self.Fitnesses = self.GetFitnesses(self.Population)
self.Sort()
self.History['Best'].append(self.Population[0])
self.History['Best F'].append(self.Fitnesses[0])
self.History['Worst F'].append(self.Fitnesses[-1])
self.History['Average F'].append(self.Fitnesses.mean())
print('Generation 0 Best: {:.2f}'.format(self.Fitnesses[0]))
for i in range(self.MaxGeneration):داخل حلقه، به ترتیب جمعیت جهشیافتهها و جمعیت فرزندان را ایجاد میکنیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Args
self.DimensionCount = LB.size
self.MutationScales = self.MutationScale * (self.UB - self.LB) / 2
self.Population = np.random.uniform(low=self.LB,
high=self.UB,
size=(self.PopulationSize,
self.DimensionCount))
self.Fitnesses = self.GetFitnesses(self.Population)
self.Sort()
self.History['Best'].append(self.Population[0])
self.History['Best F'].append(self.Fitnesses[0])
self.History['Worst F'].append(self.Fitnesses[-1])
self.History['Average F'].append(self.Fitnesses.mean())
print('Generation 0 Best: {:.2f}'.format(self.Fitnesses[0]))
for i in range(self.MaxGeneration):
M = self.GetMutants()
C = self.GetChilds()حال جمعیتهای جدید را به جمعیت موجود اضافه میکنیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Args
self.DimensionCount = LB.size
self.MutationScales = self.MutationScale * (self.UB - self.LB) / 2
self.Population = np.random.uniform(low=self.LB,
high=self.UB,
size=(self.PopulationSize,
self.DimensionCount))
self.Fitnesses = self.GetFitnesses(self.Population)
self.Sort()
self.History['Best'].append(self.Population[0])
self.History['Best F'].append(self.Fitnesses[0])
self.History['Worst F'].append(self.Fitnesses[-1])
self.History['Average F'].append(self.Fitnesses.mean())
print('Generation 0 Best: {:.2f}'.format(self.Fitnesses[0]))
for i in range(self.MaxGeneration):
M = self.GetMutants()
C = self.GetChilds()
self.Append([M, C])حال نیاز داریم تا جمعیت را براساس برازندگی مرتب کرده و اندازه آن را اصلاح کنیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Args
self.DimensionCount = LB.size
self.MutationScales = self.MutationScale * (self.UB - self.LB) / 2
self.Population = np.random.uniform(low=self.LB,
high=self.UB,
size=(self.PopulationSize,
self.DimensionCount))
self.Fitnesses = self.GetFitnesses(self.Population)
self.Sort()
self.History['Best'].append(self.Population[0])
self.History['Best F'].append(self.Fitnesses[0])
self.History['Worst F'].append(self.Fitnesses[-1])
self.History['Average F'].append(self.Fitnesses.mean())
print('Generation 0 Best: {:.2f}'.format(self.Fitnesses[0]))
for i in range(self.MaxGeneration):
M = self.GetMutants()
C = self.GetChilds()
self.Append([M, C])
self.Sort()
self.Cut()به این ترتیب هر نسل ایجاد و به اتمام میرسد. مشابه مرحله 0، نیاز داریم تا تاریخچه و نتایج را کامل کنیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Args
self.DimensionCount = LB.size
self.MutationScales = self.MutationScale * (self.UB - self.LB) / 2
self.Population = np.random.uniform(low=self.LB,
high=self.UB,
size=(self.PopulationSize,
self.DimensionCount))
self.Fitnesses = self.GetFitnesses(self.Population)
self.Sort()
self.History['Best'].append(self.Population[0])
self.History['Best F'].append(self.Fitnesses[0])
self.History['Worst F'].append(self.Fitnesses[-1])
self.History['Average F'].append(self.Fitnesses.mean())
print('Generation 0 Best: {:.2f}'.format(self.Fitnesses[0]))
for i in range(self.MaxGeneration):
M = self.GetMutants()
C = self.GetChilds()
self.Append([M, C])
self.Sort()
self.Cut()
self.History['Best'].append(self.Population[0])
self.History['Best F'].append(self.Fitnesses[0])
self.History['Worst F'].append(self.Fitnesses[-1])
self.History['Average F'].append(self.Fitnesses.mean())
print('Generation {} Best: {:.2f}'.format(i + 1, self.Fitnesses[0]))به این ترتیب روند کار الگوریتم ژنتیک در پایتون کامل خواهد بود. در انتهای متد، لیستهای موجود در دیکشنری self.History
را به آرایه Numpy
تبدیل میکنیم و در نهایت آن را برمیگردانیم:
def Maximize(self,
F:typ.Callable,
LB:np.ndarray,
UB:np.ndarray,
Args:tuple=()) -> dict:
self.F = F
self.LB = LB
self.UB = UB
self.Args = Args
self.DimensionCount = LB.size
self.MutationScales = self.MutationScale * (self.UB - self.LB) / 2
self.Population = np.random.uniform(low=self.LB,
high=self.UB,
size=(self.PopulationSize,
self.DimensionCount))
self.Fitnesses = self.GetFitnesses(self.Population)
self.Sort()
self.History['Best'].append(self.Population[0])
self.History['Best F'].append(self.Fitnesses[0])
self.History['Worst F'].append(self.Fitnesses[-1])
self.History['Average F'].append(self.Fitnesses.mean())
print('Generation 0 Best: {:.2f}'.format(self.Fitnesses[0]))
for i in range(self.MaxGeneration):
M = self.GetMutants()
C = self.GetChilds()
self.Append([M, C])
self.Sort()
self.Cut()
self.History['Best'].append(self.Population[0])
self.History['Best F'].append(self.Fitnesses[0])
self.History['Worst F'].append(self.Fitnesses[-1])
self.History['Average F'].append(self.Fitnesses.mean())
print('Generation {} Best: {:.2f}'.format(i + 1, self.Fitnesses[0]))
for k, v in self.History.items():
self.History[k] = np.array(v)
return self.Historyبه این ترتیب متد Maximize
نیز کامل میشود و الگوریتم آماده استفاده است.
تعریف تابع هدف
در ابتدای مطلب یک تابع هدف تعریف شد. تابع گفته شده را به شکل زیر تعریف میکنیم:
def F(x:np.ndarray) -> float:
y = (np.exp(-np.power(x, 2))).sum()
return yدر کد فوق، ابتدا درایههای آرایه x
به توان دوم رسیده، سپس قرینه شده و وارد تابع نمایی میشوند. یک آرایه حاصل میشود که با استفاده از متد sum
مجموعه آنها را محاسبه و برمیگردانیم. تابع فوق معادل رابطه زیر است:
$$
f ( x ) = sum _ {} ^ {} e ^ { – x _ i ^ 2 } = e ^ { – x _ 1 ^ 2 } + e ^ { – x _ 2 ^ 2 } + … + e ^ { – x _ n ^ 2 }
$$ٰ
تعریف حد بالا و پایین
حال حد بالا و پایین متغیرهای تصمیم را تعیین میکنیم:
LB = -2 * np.ones(10)
UB = +2 * np.ones(10)توجه داشته باشید که برای بررسی عملکرد، 10 متغیر تصمیم در نظر گرفتهایم. ابعاد دو آرایه فوق، نشاندهنده ابعاد فضای جستجو و تعداد متغیرهای تصمیم است.
ایجاد الگوریتم و بهینهسازی تابع هدف
حال الگوریتم را ایجاد میکنیم:
Algorithm = GA()با توجه به اینکه برای ورودیهای الگوریتم مقداری تعیین نشد، از مقادیر پیشفرض تعریف شده در حین پیادهسازی استفاده خواهد شد. حال متد Maximize
را فراخوانی و تابع هدف را به همراه حد پایین و بالا وارد آن میکنیم:
History = Algorithm.Maximize(F, LB, UB)با اجرای کد فوق، الگوریتم شروع به کار کرده و در نهایت گزارش مراحل را در دیکشنری History
برخواهدگرداند.
پس از اجرای کد، نتایج زیر نشان داده خواهد شد:
Generation 0 Best: 8.26
Generation 1 Best: 8.26
...
...
Generation 99 Best: 10.00
Generation 100 Best: 10.00به این ترتیب مشاهده میکنیم که پس از تکرارهای متوالی، الگوریتم توانسته به مقدار 10 در تابع هدف برسد. با توجه به موارد گفته شده در مورد این تابع هدف، میدانیم که بیشترین مقدار ممکن آن برابر با تعداد متغیرهای تصمیم است که 10 در نظر گرفته شده است.
رسم نمودارهای نتایج
حال براساس اطلاعات موجود در دیکشنری History
دو نمودار رسم میکنیم. اولین مورد برای مقدار تابع هدف در تمامی فراخوانیها است:
plt.plot(History['FEs'],
ls='-',
lw=0.8,
c='crimson',
label='Function Evaluations')
plt.title('Function Value Over Evaluations')
plt.xlabel('Function Evaluation')
plt.ylabel('Value')
plt.show()با اجرای کد فوق، نمودار زیر حاصل میشود:
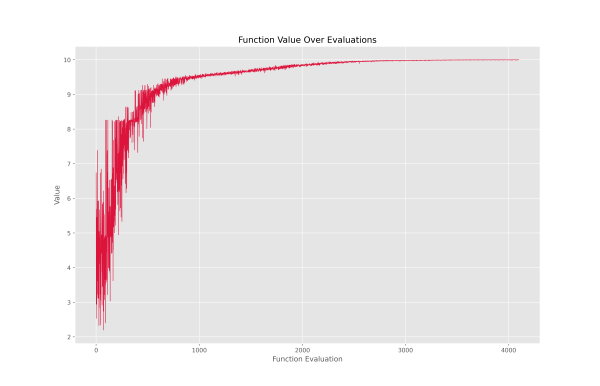
با توجه به نمودار میتوان گفت که مقادیر تابع هر در کمترین مقدار از 2.2 شروع شده است. با توجه به روند بهبود میتوان گفت که اجزای الگوریتم ژنتیک در پایتون به درستی کار خود را انجام دادهاند. آخرین داده در $$ x=4200 $$ قرار داده که به معنی 4200 بار فراخوانی تابع هدف است. پس از فراخوانی 2800، بهبود چندان بزرگی رخ نداده است، بنابراین میتوان با صرف نظر از اندکی امتیاز، زمان اجرای کد را کاهش داد. جالب توجه است که کد بهینهسازی، در زمانی حدود 200 میلیثانیه کار خود را به اتمام رسانده است.
برای بررسی این زمان، میتوان از تابع time
موجود در کتابخانه time
استفاده کرد. به عنوان نمودار دوم، سه خط مربوط به بیشترین برازندگی، کمترین برازندگی و میانگین برازندگی در طول نسلها را رسم میکنیم:
plt.plot(History['Best F'],
ls='--',
lw=1.1,
c='teal',
label='Best')
plt.plot(History['Average F'],
ls='-',
lw=0.9,
c='k',
label='Average')
plt.plot(History['Worst F'],
ls='--',
lw=1.1,
c='crimson',
label='Worst')
plt.title('Best Function Value Over Generations')
plt.xlabel('Generation')
plt.ylabel('Value')
plt.legend()
plt.show()کد فوق، نمودار زیر را ایجاد میکند:

این نمودار به جهت نمایش بهترین، بدترین و میانگین جمعیت، حائز اهمیت است.
بهبود نمودار فراخوانیهای تابع هدف الگوریتم ژنتیک در پایتون
نمودار مربوط به فراخوانیهای تابع هدف، به دلیل تعداد دادههای زیاد، نوسانات شدید دارد و این اتفاق باعث میشوند تا روند کلی دیده نشود. به همین دلیل قصد داریم یک میانگین متحرک ساده (Simple Moving Average یا SMA) بر روی آن اعمال کنیم. برای آشنایی بیشتر با میانگینهای متحرک میتوانید به مطلب «میانگین متحرک چیست؟ + پیاده سازی Moving Average در پایتون» مراجعه نمایید. به این منظور تابعی به شکل زیر برای محاسبه میانگین متحرک ساده ایجاد میکنیم:
def SMA(S:np.ndarray,
L:int) -> np.ndarray:
nD0 = S.size # Getting Input Series Size
nD = nD0 - L + 1 # Calculating Output Series Size
M = np.zeros(nD) # Creating Placeholder Array
for i in range(nD): # For Each Output Data
M[i] = S[i:i + L].mean() # Mean Over Window
return Mاز این تابع برای محاسبه میانگین متحرک ساده آرایه History[‘FEs’]
استفاده میکنیم و سپس نمودار آن را رسم میکنیم:
smaFEs = SMA(History['FEs'], 100)در این سطر، طول میانگین متحرک ساده، برابر با 100 در نظر گرفته شده است، به این ترتیب هر نقطه در نمودار، حاصل میانگین 100 نقطه اخیر خواهد بود. برای رسم نمودار به شکل زیر اقدام میکنیم:
T1 = np.arange(start=0,
stop=History['FEs'].size,
step=1)
T2 = T1[-smaFEs.size:]
plt.plot(T1,
History['FEs'],
ls='-',
lw=0.8,
c='crimson',
label='Function Evaluations')
plt.plot(T2,
smaFEs,
ls='-',
lw=1.3,
c='k',
label='SMA(100)')
plt.title('Function Value Over Evaluations + SMA(100)')
plt.xlabel('Function Evaluation')
plt.ylabel('Value')
plt.show()کد فوق پس از اجرا، نمودار زیر را نمایش خواهد داد.
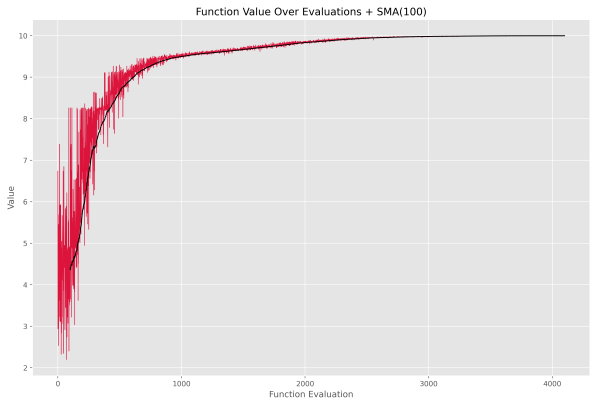
به این ترتیب روند بهبود میانگین برازندگیها مشهود است. در برخی شرایط، تشخیص بهبود جمعیت، به راحتی نمودار فوق نیست.
بررسی جواب نهایی الگوریتم ژنتیک در پایتون
جواب نهایی الگوریتم ژنتیک در پایتون به شکل زیر در دسترس است:
BestSolution = History['Best'][-1]اگر این جواب را نمایش دهیم، خواهیم داشت:
[+0.0078, -0.0087, -0.0095, +0.0058, -0.0128, +0.0034, +0.0061, -0.0201, +0.0074, +0.0086]به این ترتیب مشاهده میکنیم که اغلب موارد تا 2 رقم اعشار به 0 نزدیک شدهاند. میتوانیم در طول نسلها، فاصله بهترین جواب از جواب صحیح را محاسبه و به شکل نمودار نمایش دهیم. به این منظور ابتدا جواب بهینه را از تک تک بهترین جوابهای هر نسل کم میکنیم:
Bests = History['Best']
D = Bests - np.zeros(10)حال درایهها را به توان دوم رسانه و در بعد دوم مجموع آنها را محاسبه میکنیم:
Bests = History['Best']
D = Bests - np.zeros(10)
D2 = D ** 2
SD2 = np.sum(D2, axis=1)در نهایت باید جذر مقادیر را حساب کنیم تا فواصل اقلیدسی به دست آید:
Bests = History['Best']
D = Bests - np.zeros(10)
D2 = D ** 2
SD2 = np.sum(D2, axis=1)
Distances = np.sqrt(SD2)حال میتوانیم نمودار این فواصل را نیز رسم کنیم:
plt.plot(Distances,
ls='-',
lw=0.8,
c='crimson',
label='Distance')
plt.title('Generation's Best Solution Distance From Target Solution')
plt.xlabel('Generation')
plt.ylabel('Distance')
plt.show()با اجرای کد، نمودار زیر نمایش داده میشود.
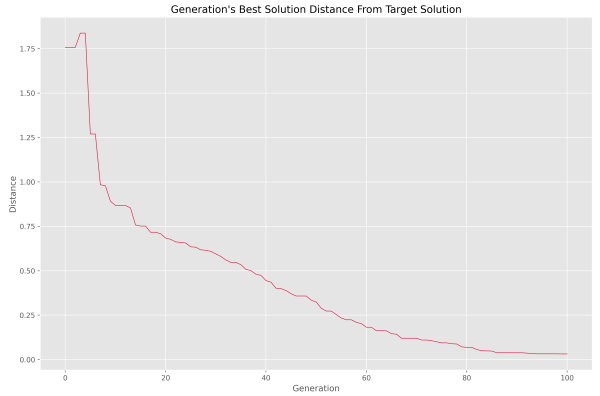
به این ترتیب مشاهده میکنیم که فاصله در حال کاهش است و به این طریق از عملکرد صحیح الگوریتم مطمئن میشویم. در صورتی که محور عمودی نمودار فوق را لگاریتمی میکردیم، نمودار به شکل زیر در میآمد.
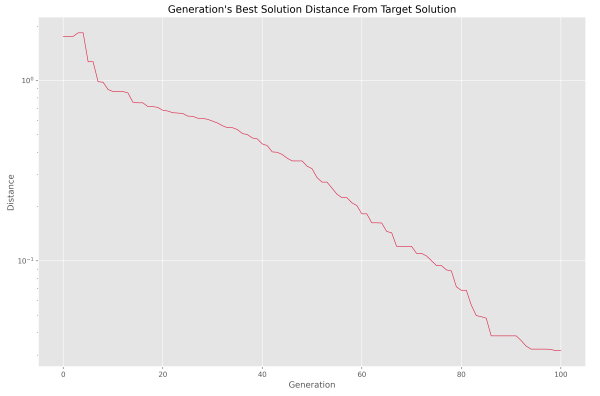
با توجه به اینکه نمودار به رفتار خطی نزدیک شده است، میتوان روند بهبود فاصله را لگاریتمی دانست. پس از نسل 80، روند از سرعت خود کاسته است. میتوان این نقطه را به عنوان نقطه پایان در نظر گرفت.
افزایش تعداد متغیرهای تصمیم الگوریتم ژنتیک در پایتون
اگر تعداد متغیرهای تصمیم را از 10 به 100 افزایش دهیم، نمودار فراخوانی تابع هدف به شکل زیر درمیآید.
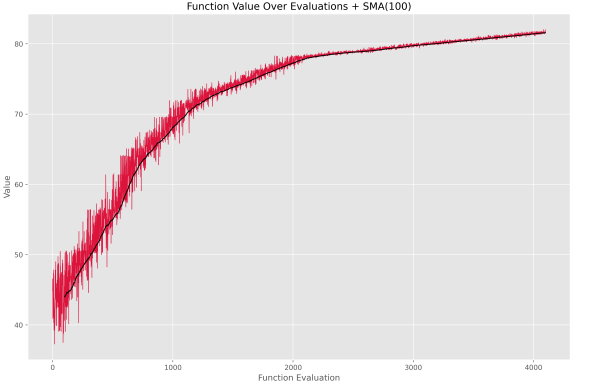
میتوان مشاهده کرد که الگوریتم با 4200 بار فراخوانی تابع هدف، توانسته به خوبی به عدد 82 برسد. توجه داشته باشید که در این شرایط بیشترین مقدار ممکن برای تابع هدف برابر با 100 است. زمان اجرای الگوریتم برای این شرایط، حدود 1100 میلیثانیه است.
چگونه یک مدل رگرسیون خطی را با استفاده از الگوریتم ژنتیک در پایتون آموزش دهیم ؟
به این منظور یک مجموعه داده مصنوعی براساس ضابطه زیر ایجاد میکنیم:
$$
y=b+w_1×x_1+w_2×x_2+w_3×x_3+w_4×x_4
$$
برای تولید مجوعه داده به عنوان b از عدد 1.3 استفاده میکنیم و به عنوان ضرایب از اعداد زیر:
$$
W=[1.2 , -2.1 , 1.6 , -0.8]
$$
قصد داریم تا با استفاده از الگوریتم ژنتیک این پارامترها را محاسبه کنیم. به این ترتیب با داشتن جواب مسئله، قادر خواهیم بود عملکرد کد پیادهسازی شده را دریابیم. برای تولید مجموعه داده به شکل زیر عمل میکنیم:
N = 1000
nX = 4
W = np.array([1.2, -2.1, 1.6, -0.8])
B = 1.3
X = np.random.uniform(low=-5, high=+5, size=(N, 4))
Y = np.dot(X, W) + Bبرای تعیین حد پایین و بالا نیز کد زیر را استفاده میکنیم:
LB = -10 * np.ones(nX + 1)
UB = +10 * np.ones(nX + 1)حالا نیاز داریم تا تابع برازندگی یا تابع هدف را تغییر دهیم. این تابع اسم R2
را به خود خواهد گرفت و در ورودی متغیرهای تصمیمگیری به همراه مجموعه داده را دریافت خواهد کرد:
def R2(x:np.ndarray,
X:np.ndarray,
Y:np.ndarray) -> float:
B = x[0]
W = x[1:]
P = np.dot(X, W) + B
MSE = ((Y - P) ** 2).mean()
Variance = Y.var()
r2 = 100 * (1 - MSE / Variance)
return r2این تابع در خروجی ضریب تعیین (Coefficient of Determination یا R^2 Score) که یک معیار ارزیابی برای رگرسیون است را برمیگرداند. برای آشنایی بیشتر با معیارهای ارزیابی رگرسیون، میتوانید به مطلب «بررسی معیارهای ارزیابی رگرسیون در پایتون – پیاده سازی + کد» مراجعه نمایید. برای ایجاد و اجرای الگوریتم نیز کد زیر را استفاده میکنیم:
Algorithm = GA()
History = Algorithm.Maximize(R2, LB, UB, Args=(X, Y))توجه داشته باشید که در این مثال، تابع هدف بیش از یک ورودی دریافت میکند، به همین دلیل لازم است که ورودیهای به جز ورودی اول به عنوان Args
در ورودی متد Maximize
اضافه شود. کد در مدت 250 میلیثانیه، بهینهسازی مدل رگرسیون را به اتمام میرساند. دقت نهایی مدل به 99.99% میرسد که بسیار جالب توجه است. نمودار فراخوانی توابع به شکل زیر است.
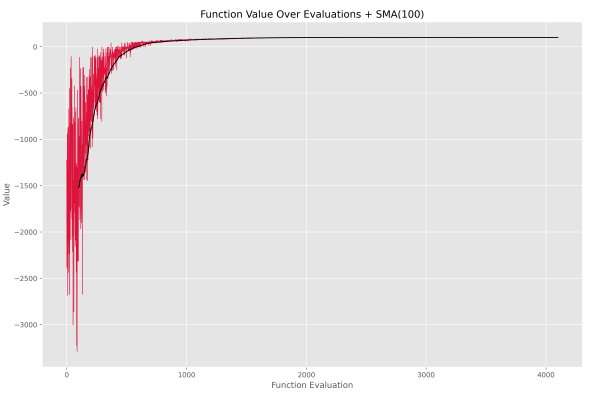
به این ترتیب روند بهبود جمعیت به خوبی معلوم میشود. در انتهای کد، وزنها و مقدار بایاس به صورت زیر است:
B = +1.2869
W = [+1.2034, -2.0827, +1.6022, -0.7886]با مقایسه پارامترهای حاصل با پارامترهای تعیین شده توسط ما، متوجه میشویم که الگوریتم تخمین خوبی از این پارامترها داشته است. به این ترتیب پیادهسازی و آزمایش الگوریتم ژنتیک به اتمام میرسد. برای مطالعه بیشتر، میتوان موارد زیر را بررسی کرد:
- در طول روند کار الگوریتم، جهش و آمیزش هرکدام در ابتدا و انتهای اجرا چه مقدار به بهبود عملکرد الگوریتم کم کردهاند؟
- یک مدل غیرخطی را با استفاده از الگوریتم ژنتیک پیادهسازی شده، آموزش دهید.
- در برخی موارد، Max Generation
تعیین شده، بیشتر از مقدار مورد نیاز مسئله است و در نسلهای انتهایی، بهبود چندانی رخ نمیدهد. در این شرایط، پراکندگی بین بهترین کروموزومهای آخرین نسلها کاهش مییابد. کد نوشته شده را به گونهای تغییر دهید که به صورت خودکار در صورت مواجه با چنین شرایطی، اجرای الگوریتم را ادامه ندهد.
- برخی توابع هدف Keyword Argument دریافت میکنند. برای رفع این مشکل، کد را بهبود ببخشید.
- ممکن است کاربر، اشتباها حد بالا و حد پایینها را به صورت جابهجا وارد نماید (برای یک یا چند متغیر تصمیم، حد بالا کوچکتر از حد پایین باشد). برای به اطلاع رساندن این مشکل و جلوگیری از ادامه کار کد، از دستور assert
استفاده کنید.
- در برخی موارد، انتخاب والدین یا کروموزوم اولیه برای جهش، بدون جایگذاری انجام میشود. الگوریتم را برای کار در این شرایط اصلاح کنید.
- اثر هریک از پارامترهای تنظیمکننده الگوریتم بر روی عملکرد الگوریتم را بررسی نمایید.
- چه رابطهای بین دفعات فراخوانی تابع هدف با تنظیمات الگوریتم وجود دارد؟

