پیاده سازی الگوریتم خوشه بندی K-means در پایتون — راهنمای گام به گام

الگوریتم K-means یا همان خوشه بندی K میانگین (K-means Clustering)، یکی از ساده‌ترین و رایج‌ترین الگوریتم‌های نوع بدون نظارت‌ یا همان نظارت نشده و خوشه بندی در یادگیری ماشین به حساب می‌آید. الگوریتم خوشه بندی K-means برای پیدا کردن دسته‌هایی در داده‌ها مورد استفاده قرار می‌گیرد که برچسب مشخصی ندارند. K-means می‌تواند برای تایید فرضیات تجاری درباره اینکه چه نوع دسته‌ها و نظم‌هایی در داده‌ها وجود دارند یا برای شناسایی دسته‌های ناشناخته در مجموعه داده‌های پیچیده به کار گرفته شود. در این مقاله، ابتدا به این سوال پاسخ داده می‌شود که K-means چیست و سپس آموزش پیاده سازی K-means در پایتون به بیان ساده و به صورت گام به گام ارائه شده است.

الگوریتم K-means چیست ؟

K-Means یکی از پرکاربردترین الگوریتم‌های خوشه‌بندی داده‌ها به شمار می‌رود. در K-means با تکرار اعمالی ثابت و استفاده از توابعی مانند Norm ،Mean و Argmin، می‌توان به ازای هر خوشه، مراکزی را یافت که دقت بالا و لَختی (اینرسی) کمی دارند.

فیلم آموزش خوشه بندی K میانگین K-Means با اس پی اس اس SPSS در تم آف

کلیک کنید

هدف در الگوریتم K-means ، کمینه‌سازی فاصله میان نقطه‌ها (داده‌ها) در یک خوشه است. K-means یک الگوریتم مبتنی بر مرکز یا مبتنی بر فاصله است که در آن فاصله‌ها برای تخصیص دادن یک نقطه به یک خوشه محاسبه می‌شوند. در K-means هر خوشه یک مرکز دارد. هدف اصلی الگوریتم K-means ، کمینه‌سازی مجموع فاصله‌های میان نقاط با مرکز خوشه مربوطه است.

مراحل اجرای الگوریتم K-means چیست ؟

به طور کلی، گام‌های اجرای الگوریتم K-means به شرح زیر است:

فیلم آموزش خوشه بندی K میانگین K-Means با اس پی اس اس SPSS

کلیک کنید

1. تعیین تعداد خوشه‌ها (K)
2. انتخاب K عدد تصادفی از داده‌ها به عنوان مختصات مراکز خوشه‌ها
3. تخصیص تمام نقاط (داده‌ها) به نزدیک‌ترین مرکز خوشه
4. انتخاب میانگین وزن‌دار داده‌های هر خوشه به عنوان مرکز آن
5. تکرار گام‌های ۳ و ۴ تا زمانی که معیار توقف برقرار شود.

معیارهای توقف برای الگوریتم K-means چیست ؟

اساساً می‌توان سه معیار توقف را برای متوقف کردن حلقه تکرار الگوریتم K-means به کار گرفت. این سه معیار در ادامه فهرست شده‌اند:

فیلم آموزش کاهش تعداد رنگ تصاویر با استفاده از روش های خوشه بندی هوشمند در تم آف

کلیک کنید

1. مرکزهای خوشه‌های ایجاد شده جدید تغییر نکنند.
2. نقطه‌ها (داده‌ها) در همان خوشه باقی بمانند و تغییر در عضویت خوشه برای داده‌ها ایجاد نشود.
3. تعداد تکرارها به تعداد تکرار بیشینه (تعیین شده) برسد.

رابطه ریاضی الگوریتم K-means چیست ؟

این الگوریتم، به زبان ریاضی، به شکل زیر در خواهد آمد:

$$ C_j = mean( A_j(t-1)), t geqslant 1 $$

$$ A_j(t) = { X_i mid X_i in X, j = mathop{argmin}_{textbf{j}} ( norm(X_i – C_j (t))) } $$

در ادامه مقاله K-means چیست ، پیاده سازی این الگوریتم در پایتون آموزش داده شده است. اما پیش از آن، مجموعه دوره‌های آموزش داده کاوی و یادگیری ماشین تم آف به علاقه‌مندان به این حوزه معرفی شده است.

پیاده سازی K-means در پایتون

در این بخش از مقاله K-means چیست آموزش پیاده سازی الگوریتم K-means در پایتون به صورت گام به گام ارائه شده است. گام اول، فراخوانی کتابخانه‌های مورد استفاده است.

فیلم آموزش کاهش تعداد رنگ تصاویر با استفاده از روش های خوشه بندی هوشمند در تم آف

کلیک کنید

فراخوانی کتابخانه‌ها برای پیاده سازی الگوریتم K-means در پایتون

پیاده سازی الگوریتم K-means در پایتون از کتابخانه‌های numpy‌ و Matplotlib استفاده می‌شود، بنابراین باید وارد محیط برنامه‌نویسی شده و این کتابخانه‌ها را فراخوانی کرد:

import numpy as np
import matplotlib.pyplot as plt

در مرحله بعد، باید داده‌های مصنوعی برای اجرای K-means روی آن‌ها تعریف شوند. این کار در ادامه این بخش از مقاله K-means چیست انجام شده است.

فیلم آموزش کتابخانه های NumPy و Matplotlib در پایتون در تم آف

کلیک کنید

تولید داده‌های مصنوعی برای پیاده سازی الگوریتم K-means در پایتون

پس از فراخوانی کتابخانه‌های مورد نیاز برای پیاده سازی الگوریتم K-means در پایتون ، باید یک مجموعه داده با مرکزهای خوشه تعیین شده (مشخص) تولید شود تا در نهایت بتوان نتایج حاصل شده از اجرای الگوریتم K-means را با مقادیر واقعی مقایسه کرد.

فیلم آموزش خوشه بندی با الگوریتم های تکاملی و فراابتکاری در تم آف

کلیک کنید

کدهای تولید داده‌های مصنوعی با مرکزهای خوشه مشخص در پایتون به صورت زیر است:

def CreateDataset(Cs, nD, S):
    nC = len(Cs)
    N = nD * nC
    X = np.zeros((N, 2))
    for i in range(0, nD):
        for j in range(0, nC):
            X[nC*i + j, 0] = Cs[j, 0] + np.random.randn() / S
            X[nC*i + j, 1] = Cs[j, 1] + np.random.randn() / S
    return X

در تابع CreateDataset که در کدهای فوق ایجاد شده است، حول هر مرکز ورودی، به تعداد nD داده به صورت تصادفی ایجاد و در خروجی بازگردانده می‌شود.

فراخوانی تابع تولید داده‌های مصنوعی

فراخوانی تابع CreateDataset به صورت زیر است:

# Centers of Synthetic Data
Cs = np.array([[-0.5, +1.0], [+1.6, -0.1],
                [-0.9, -1.7], [-2.9, +2.3],
                [+0.7, +2.2], [-2.2, +0.3]])
nD = 200 # Count of Data in Each Cluster
S = 2.5

X = CreateDataset(Cs, nD, S)

در کدهای فوق، ابتدا پارامترهای ورودی تابع CreateDataset شامل nD ،Cs و S تعریف و مقداردهی شده‌اند. سپس، تابع CreateDataset فراخوانی و متغیرهای تعریف شده به عنوان ورودی به این تابع ارجاع داده می‌شوند. ‌پس از اجرای تابع، داده‌های مورد نیاز در آرایه‌ی X ذخیره خواهند شد.

فیلم آموزش کتابخانه Matplotlib برای ترسیم و بصری سازی داده ها در پایتون در تم آف

کلیک کنید

بصری‌سازی داده‌های تولید شده

برای نمایش و بصری‌سازی داده‌های تولید شده می‌توان داده‌ها را به یک صورت نمودار توزیعی (Scatter Plot) رسم کرد:

plt.style.use('ggplot')
plt.scatter(X[:, 0], X[:, 1], c = 'k', s = 9, label = 'Data')
plt.scatter(Cs[:,0], Cs[:, 1], c = 'r', s = 100, label = 'Center', marker = '*')
plt.title('Scatter Plot of Data')
plt.xlabel('X1')
plt.ylabel('X2')
plt.legend()
plt.show()

باید توجه داشت که در کدهای فوق، دوبار از دستور plt.scatter استفاده شده است. در اولین فراخوانی plt.scatter، توزیع داده‌های ماتریس X و در فراخوانی دوم، مراکز خوشه‌ها رسم شده‌اند. در این مقاله برای پیاده سازی الگوریتم K-means در پایتون از داده‌های دو بُعدی استفاده شده است. این کار با هدف ساده‌سازی محاسبات و امکان نمایش داده‌ها در نمودار صورت گرفته است. می‌توان با تغییر دادن ابعاد X در تابع CeateDataset، داده‌هایی با ابعاد بالاتر ایجاد کرد. نمودار توزیعی کدهای فوق در خروجی به صورت زیر چاپ می‌شود:

فیلم آموزش کتابخانه Matplotlib برای ترسیم و بصری سازی داده ها در پایتون در تم آف

کلیک کنید

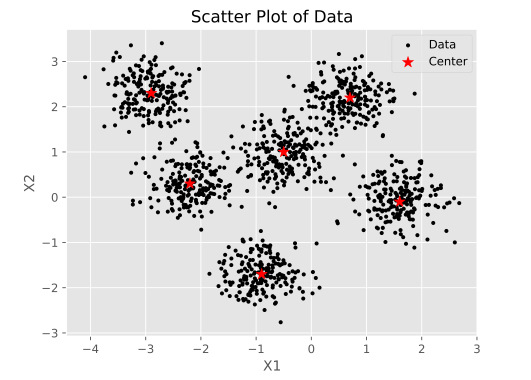
تعیین تعداد خوشه‌ها مراکز آن‌‌ها

nClusters = 6

Centers = np.random.uniform(-2, +2, (nClusters, 2)) # Initializing Centers Posotions

در کدهای فوق باید توجه داشت که برای تعیین مراکز خوشه تصادفی می‌توان بازه‌های پایین و بالا را تغییر داد. با توجه به اینکه داده‌های تولید شده دارای دو بُعد هستند، مراکز خوشه‌ها نیز در یک محیط دو بُعدی قرار خواهند گرفت.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در تم آف

کلیک کنید

ایجاد تابعی برای تخصیص هر داده به یک خوشه

در مرحله بعد، باید تابعی ایجاد شود که با دریافت مختصات مراکز خوشه‌ها و نقاط موجود در $$ X $$، هر داده را به نزدیک‌ترین خوشه اختصاص داده و در نهایت آرایه‌ای از داده‌های موجود در هر خوشه بازگردانده شود. این تابع به صورت زیر تعریف می‌شود:

def GetClusters(Centers, nClusters, X):

ایجاد یک لیست برای ذخیره داده‌های هر خوشه

اکنون باید یک لیست ایجاد شود که در آن به تعداد nClusters لیست خالی وجود داشته باشد تا بعداً هر داده به لیست مربوط به آن خوشه اضافه شود:

def GetClusters(Centers, nClusters, X):
    Clusters = []
    for i in range(0, nClusters):
        Clusters.append([])

در خروجی کدهای فوق، لیست Clusters، به شکل زیر خواهد بود:

$$ Clusters = [ [spacespacespace], [spacespacespace], dots, [spacespacespace] ] $$

محاسبه فاصله هر نقطه از مرکز

حال باید به ازای هر داده‌ $$ X_i $$، فاصله را از هر مرکزِ $$ C_j $$ محاسبه کرد. برای انجام این کار، ابتدا حلقه‌ای به ازای تمامی داده‌ها ایجاد و سپس یک آرایه خالی برای افزودن فاصله هر مرکز از $$ X_i $$ تعریف می‌شود.

فیلم آموزش یادگیری ماشین و پیاده سازی در پایتون Python – بخش یکم در تم آف

کلیک کنید

پس از آن، باید به ازای تمامی مراکز خوشه‌ها، فاصله $$ X_i $$ تا $$ C_j $$ را محاسبه کرد. این موارد در کدهای زیر انجام شده است:

for xi in X:
        d = np.zeros(nClusters)
        for j in range(0, nClusters):
            cj = Centers[j]
            dij = xi - cj
            d[j] = np.linalg.norm(dij)

در کدهای فوق، با کم کردن دو بردار $$ X_i $$ و $$ C_j $$ از یکدیگر، بردار $$ D_(i,j) $$ حاصل می‌شود که مقدار L2-Norm آن، بیان‌گر فاصله اقلیدسی خواهد بود. تابع norm به طور پیش‌فرض، از روش L2 استفاده می‌کند. البته در صورت نیاز، می‌توان از روش‌های دیگر نیز استفاده کرد. حال باید داده $$ X_i $$ را به لیست مربوط به نزدیک‌ترین مرکز خوشه اضافه کرد:

        a = np.argmin(d) # Arg of Nearest Center
        Clusters[a].append(xi) # Appending Xi to Nearest Centers List

به این ترتیب، تابع مورد نظر تا به اینجا کامل شده و عملکرد مورد نیاز را انجام می‌دهد.

تبدیل لیست‌های خوشه‌ها به آرایه

بهتر است در انتها، لیست‌های موجود در Clusters به آرایه تبدیل شوند تا استفاده از آن‌ها، راحت‌تر باشد:

def GetClusters(Centers, nClusters, X):
    Clusters = []
    for i in range(0, nClusters):
        Clusters.append([])
    for xi in X:
        d = np.zeros(nClusters)
        for j in range(0, nClusters):
            cj = Centers[j]
            dij = xi - cj
            d[j] = np.linalg.norm(dij)
        a = np.argmin(d) # Arg of Nearest Center
        Clusters[a].append(xi) # Appending Xi to Nearest Centers List
    for i in range(0, nClusters):
        Clusters[i] = np.array(Clusters[i])
    return Clusters

اکنون می‌توان در متن اصلی برنامه، از تابع ایجاد شده استفاده کرد:

nClusters = 6

Centers = np.random.uniform(-2, +2, (nClusters, 2)) # Initializing Centers Posotions
Clusters = GetClusters(Centers, nClusters, X)

پیاده سازی گام‌های تکرار شونده ۳ و ۴ الگوریتم K-means در پایتون

تا این مرحله در مقاله «K-means چیست»، گام‌های 1 و 2 الگوریتم K-means کامل و در پایتون پیاده سازی شده‌اند، حال برای پیاده سازی تکرار مراحل 3 و 4، نیاز به ایجاد یک حلقه وجود دارد:

nIter = 20

for i in range (0, nIter):

ابتدا باید در هر مرحله مختصات مراکز خوشه‌ها به‌روز شوند. برای این فرآیند، باید یک تابع به صورت زیر تعریف کرد:

def UpdateCenters(Centers, Clusters, nClusters):

اکنون باید به ازای هر خوشه، مرکز مربوطه، در میانگین نقاط مربوط به آن خوشه قرار گیرد:

def UpdateCenters(Centers, Clusters, nClusters):
    for i in range(0, nClusters):
        Centers[i] = np.mean(Clusters[i], axis = 0)

به این ترتیب، مقادیر با استفاده از تابع np.mean به روزرسانی می‌شوند. نکته مهمی که در این مرحله وجود دارد، مقدار axis است. مقدار axis در این موارد، باید برابر صفر باشد تا عمل میانگین‌گیری به ازای هر سطر انجام نشود، بلکه باید به ازای هر ستون صورت گیرد. مشکلی که ممکن است در این بخش به وجود آید، خالی بودن آرایه مربوط به یک خوشه است.

فیلم آموزش کاهش تعداد رنگ تصاویر با استفاده از روش های خوشه بندی هوشمند در تم آف

کلیک کنید

در چنین شرایطی، مقدار میانگین به عدد $$ frac{0}{0} $$ خواهد رسید که باعث اختلال در اجرای برنامه می‌شود. به همین دلیل، باید شرطی تعیین کرد تا عمل به روزرسانی در صورتی انجام شود که آرایه مربوطه خالی نیست:

def UpdateCenters(Centers, Clusters, nClusters):
    for i in range(0, nClusters):
        if np.size(Clusters[i]) != 0: # if Array is not Empty
            Centers[i] = np.mean(Clusters[i], axis = 0)
    return Centers

به این ترتیب، تابع مورد نیاز برای به‌روزرسانی مراکز ایجاد شده است. حالا باید حلقه‌ی ایجاد شده را تکمیل کرد:

nIter = 20

for _ in range (0, nIter):
    Centers = UpdateCenters(Centers, Clusters, nClusters)
    Clusters = GetClusters(Centers, nClusters, X)

بنابراین، پیاده سازی الگوریتم K-means در پایتون انجام شده است و الگوریتم K-means به درستی عمل خواهد کرد.

مقایسه نتایج پیاده سازی شده الگوریتم K-means با مراکز خوشه واقعی

پس از اتمام مراحل، می‌توان نمودار مختصات مراکز حاصل از الگوریتم K-Means را با مراکزی که تعیین شده بودند، مقایسه کرد.

plt.scatter(Cs[:,0], Cs[:,1], label='Target Centers', marker = '*', s = 80, c = 'r')
plt.scatter(Centers[:,0], Centers[:,1],
            label='Centers Found by K-Means', marker = 'x', s = 60, c = 'k')
plt.xlabel('X1')
plt.ylabel('X2')
plt.legend()
plt.show()

پس از اجرای کدهای فوق، تصویر خروجی به صورت زیر خواهد بود:

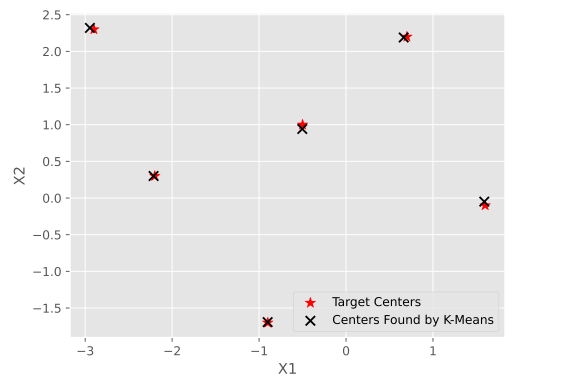
نمایش بصری مراحل الگوریتم K-means

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین در تم آف

کلیک کنید

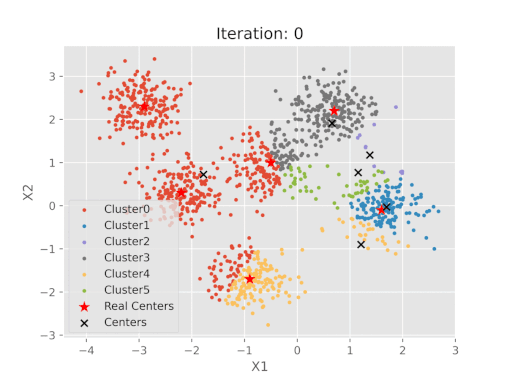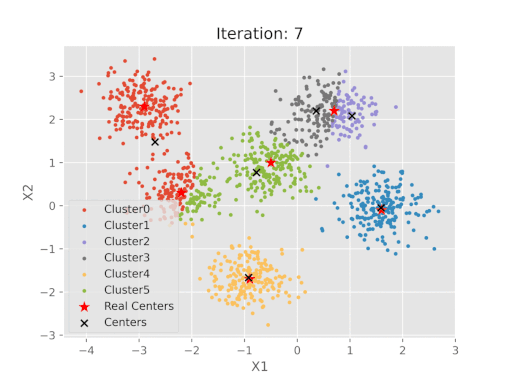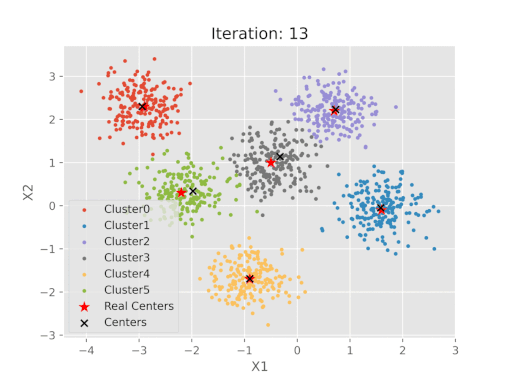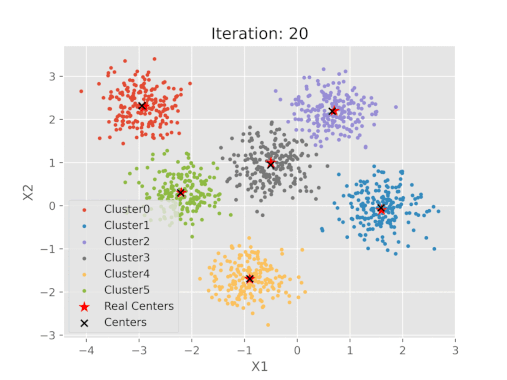
جمع‌بندی

در این مقاله، ابتدا به این سوال پاسخ داده شد که الگوریتم k-means چیست و سپس پیاده سازی الگوریتم K-means در پایتون به صورت گام به گام و تا حد امکان به بیان ساده ارائه شد. در این پیاده سازی ابتدا داده‌های مصنوعی تولید و مراکز خوشه برای آن‌ها تعیین شد. سپس، کدها و توابع لازم برای پیاده سازی K-means ایجاد شدند و این الگوریتم روی داده‌های تولید شده اجرا و نتایج آن با مراکز تعیین شده برای خوشه‌ها مقایسه شد.