میانگین متحرک چیست؟ + پیاده سازی Moving Average در پایتون

در علم آمار، میانگین متحرک (Moving Average) به محاسباتی گفته می‌شود که برای تجزیه و تحلیل نقاط داده به وسیله میانگین‌گیری زیرمجموعه‌های مختلفی از کل مجموعه داده انجام می‌شود. در این مقاله، ابتدا به این سوال پاسخ داده شده که میانگین متحرک چیست و سپس «میانگین متحرک ساده» (Simple Moving Average | SMA) شرح داده شده است. همچنین، به کاربردها و انواع میانگین متحرک اشاره می‌شود. در پایان نیز میانگین متحرک در پایتون پیاده‌سازی خواهد شد. دوره‌های آموزشی مرتبط با مفاهیم بیان شده در این مقاله نیز در انتها معرفی شده‌اند.

برای پاسخ به این سوال که میانگین متحرک چیست ، ابتدا بهتر است در قالب یک مقدمه، پیرامون مفهوم «میانگین» (Average) توضیحاتی ارائه شود.

میانگین چیست ؟

«میانگین» معیاری معروف و رایج است که معمولاً در اغلب امور مرتبط با داده‌ها کاربرد دارد. در میانگین‌گیری معمولی، از تمامی داده‌های موجود در مجموعه فرضی $$X$$ استفاده می‌شود و خروجی حاصل از محاسبه میانگین ، تنها یک عدد واحد است.

فیلم آموزش آمار و احتمال مهندسی در تم آف

کلیک کنید

برای مثال، فرض می‌شود مجموعه X به صورت زیر باشد:

$$ ? = {1, 1, 2, 3, 5, 8, 13, 21} $$

اگر $$‎overline{X}‎$$ نماد میانگین برگرفته از تمامی داده‌ها در نظر گرفته شود، مقدار آن به صورت زیر محاسبه خواهد شد:

$$ ‎overline{X}‎ = frac{Sigma_{i=1}^n X_i}{n} $$

میانگین متحرک چیست ؟

در مواردی که داده‌ها دارای نظم زمانی هستند (سری‌های زمانی)، می‌توان به جای کل داده‌ها، بخشی از آن‌ها را برای میانگین‌گیری استفاده کرد. جهت روشن‌تر شدن این موضوع و ارائه مقدمه‌ای برای تعریف «میانگین متحرک ساده» (Simple Moving Average | SMA)، در ادامه مثالی ارائه شده است.

فیلم آموزش میانگین متحرک – تحلیل تکنیکال در بورس و سرمایه گذاری در بازارهای مالی با Moving Average در تم آف

کلیک کنید

مثالی برای درک بهتر میانگین متحرک ساده

برای مثال، می‌توان زیرمجموعه‌های زیر را از $$X$$ استخراج و برای هر کدام یک میانگین محاسبه کرد:

$$ T_3 = {X_1, X_2, X_3 } = { 1, 1, 2 } Rightarrow M_3 = frac{1+1+2}{3} = frac{4}{3} $$

$$ T_4 = {X_2, X_3, X_4 } = { 1, 2, 3 } Rightarrow M_4 = frac{1+2+3}{3} = frac{6}{3} $$

$$ vdots $$

$$ T_8 = {X_6, X_7, X_8 } = { 8, 13, 21 } Rightarrow M_8 = frac{8+13+21}{3} = frac{42}{3} $$

حال می‌توان گفت، مقدار «میانگین متحرک ساده» با طول پنجره 3 در زمان $$t$$ به صورت زیر محاسبه می‌شود:

با محاسبه همه مقادیر، مجموعه M به صورت زیر خواهد بود:

$$ M = {frac{4}{3}, frac{6}{3}, frac{10}{3}, frac{16}{3}, frac{26}{3}, frac{42}{3}} $$

از آنجایی که این میانگین با حرکت دادن (Moving) پنجره دید بر روی داده‌ها حاصل می‌شود، به آن میانگین متحرک می‌گویند. باید توجه داشت که مقدار میانگین متحرک برای زمان‌های $$ t = 1$$ و $$ t = 2 $$ تعریف نشده است.

میانگین متحرک ساده چیست ؟

به بیان ساده و به طور خلاصه، میانگین متحرک ساده که به اختصار SMA خطاب می‌شود، به وسیله میانگین‌گیری از یک مجموعه داده در طول یک بازه زمانی مشخص محاسبه می‌شود. به بیان دیگر، برای SMA، میانگین یک مجموعه از اعداد یا در علوم و بازارهای مالی، یک مجموعه از قیمت‌ها در طول یک بازه زمانی تعیین شده محاسبه می‌شود.

فیلم آموزش تجزیه و تحلیل داده های مالی با پایتون – بخش یکم در تم آف

کلیک کنید

یعنی این قیمت‌ها در بازه زمانی مربوطه با هم جمع و بر تعداد اعضای مجموعه تقسیم می‌شود. فرمول محاسبه میانگین متحرک ساده یا همان SMA به صورت زیر است:

$$ SMA = frac{A_1 + A_2 + … + A_n}{n} $$

در فرمول فوق به ترتیب، $$ SMA $$ «مقدار میانگین متحرک ساده»، $$ A_n $$ «مقدار داده $$ n$$ام در یک بازه زمانی» و $$ n $$ نیز «تعداد داده‌ها در یک بازه زمانی» هستند. در فرمول فوق، $$ SMA $$ مقدار میانگین متحرک را در بازه زمانی $$ t_n$$ محاسبه می‌کند. با محاسبه $$ SMA $$ برای بازه‌های زمانی دیگر و مصورسازی آن در نمودار می‌توان روند تغییرات میانگین متحرک را مورد تحلیل و بررسی قرار داد.

کاربردهای میانگین متحرک چه هستند؟

از میانگین متحرک برای اهداف متفاوتی استفاده می‌شود. میانگین متحرک در دو حوزه‌های علوم مالی و علم داده کاربرد برجسته‌ای دارد. بنابراین، در ادامه این بخش از مقاله «میانگین متحرک چیست»، به شرح مختصری از کاربرد آن در این دو حوزه پرداخته شده است.

فیلم آموزش اندیکاتور همگرایی – واگرایی میانگین متحرک MACD در تم آف

کلیک کنید

کاربرد میانگین متحرک در علوم مالی

میانگین متحرک در علوم مالی و تحلیل تکنیکال بخش جداناپذیری از شاخص‌ها (اندیکاتورها) به حساب می‌آید. هرچند خود میانگین متحرک به تنهایی یک اندیکاتور پرکاربرد است، در ترکیب با سایر اندیکاتورها نیز به خوبی عمل می‌کند.

کاربرد میانگین متحرک در علم داده

در علم داده از میانگین متحرک برای «شناسایی روند» (Trend Detection) استفاده می‌شود. در تحلیل سری زمانی، ابتدا باید روند را از داده‌ها حذف کرد که به این عمل «Detrending» گفته می‌شود و استفاده از میانگین متحرک یک روش متداول برای این کار به حساب می‌آید.

فیلم آموزش میانگین متحرک – تحلیل تکنیکال در بورس و سرمایه گذاری در بازارهای مالی با Moving Average در تم آف

کلیک کنید

با توجه به اینکه میانگین متحرک تنها از آخرین داده اثر نمی‌پذیرد، رفتار و تغییرات آن نیز تنها وابسته به آخرین داده نیست. این ویژگی میانگین متحرک باعث ایجاد تاخیر در واکنش آن می‌شود. اما، از آنجا که حاصل، میانگین‌گیری از چندین داده است، اعتبار آن بیش‌تر و نسبت به نوسانات حساسیت کم‌تری دارد. حال در ادامه مقاله «میانگین متحرک چیست» به انواع مختلف میانگین متحرک اشاره شده است.

انواع میانگین متحرک کدامند؟

میانگین‌های متحرک دارای انواع مختلفی هستند که هر یک از آن‌ها در ادامه فهرست شده‌اند:

1. میانگین متحرک ساده (Simple Moving Average)
2. میانگین متحرک نمایی (Exponential Moving Average)
   1. میانگین متحرک نمایی
   2. میانگین متحرک نمایی دوگانه
   3. میانگین متحرک نمایی سه‌گانه
3. میانگین متحرک وزن‌دار (Weighted Moving Average)
4. میانگین متحرک بدون تاخیر (Zero-Lag Exponential Moving Average)

فیلم آموزش روش های پارامتریک و غیر پارامتریک حذف گرایش یا Trend از سری های زمانی (رایگان) در تم آف

کلیک کنید

تفاوت تمامی این موارد، تنها در روش و چگونگی وزن‌دهی به داده‌ها است. میانگین متحرک ساده به تمامی داده‌های درون پنجره به یک اندازه وزن می‌دهد:

$$ SMA_t‎ = frac{largeSigma_{i=t}^{t+L} x_t}{L} = frac{1}{L}largeSigma_{i=t}^{t+L} {x_t} $$

اما در سایر روش‌ها، رویکرد متفاوتی در وزن‌دهی وجود دارد که باعث ایجاد مزایا و معایبی برای آن‌ها می‌شود. حال در ادامه، میانگین متحرک ساده در پایتون به صورت عملی پیاده‌سازی شده است. پیش از آن، مجموعه دوره‌های آموزشی تحلیل تکنیکال تم آف به علاقه‌مندان معرفی شده است.

پیاده سازی میانگین متحرک ساده در پایتون

در این بخش از مقاله «میانگین متحرک چیست» پیاده سازی میانگین متحرک ساده در پایتون آموزش داده شده است. این آموزش به صورت گام به گام ارائه می‌شود. در گام اول باید کتابخانه‌های مورد نیاز را فراخوانی کرد. این کار در ادامه انجام شده است.

فیلم آموزش میانگین متحرک – تحلیل تکنیکال در بورس و سرمایه گذاری در بازارهای مالی با Moving Average در تم آف

کلیک کنید

فراخوانی کتابخانه های مورد نیاز برای پیاده سازی میانگین متحرک در پایتون

برای پیاده سازی میانگین متحرک ساده در پایتون ، ابتدا باید کتابخانه‌های مورد نیاز را فراخوانی کرد:

import numpy as np
import matplotlib.pyplot as plt

حال نیاز به داده‌هایی برای میانگین‌گیری وجود دارد.

تولید داده مصنوعی برای پیاده سازی میانگین متحرک در پایتون

اکنون با ایجاد و استفاده از یک تابع، ۵۰ داده مصنوعی تولید می‌شود:

def Seri(N):
    X = np.arange(0, N, 1)
S = 0.9*np.sin(X/8) - 0.9*np.sin(2+X/5) + 0.4*np.sin(4+X/2) - 2*X/N
    return S

N = 50 # Data Size
S = Seri(N) # Time Seri Data

همان‌طور که در کدهای فوق ملاحظه می‌شود، این تابع (S) از حاصل جمع سه تابع سینوسی با فرکانس و شدت متفاوت به همراه یک خط ایجاد شده است.

نمایش و رسم داده‌های مصنوعی تولید شده

حال باید کدنویسی لازم برای نمایش و رسم داده‌ها را انجام داد:

plt.style.use('ggplot')
plt.plot(np.arange(1, N+1), S, label = 'Seri Data',
        c = 'b', linewidth = 0.8, marker = 'o',
        ms = 4, mfc = 'r', mec = 'r')
plt.xlabel('T')
plt.ylabel('Y')
plt.legend()
plt.show()

خروجی و نمودار حاصل برای داده‌های اصلی به صورت زیر است:

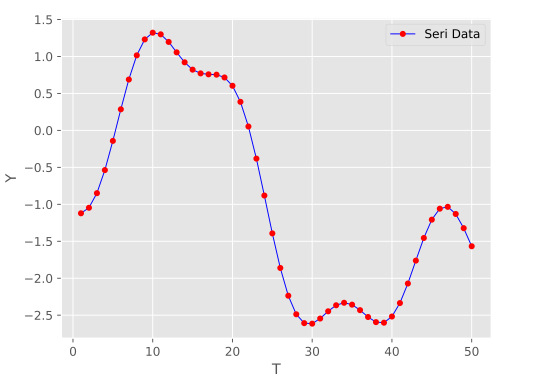
در تصویر فوق مشاهده می‌شود که داده‌ها در بازه 1 تا 50 قرار دارند و دارای رفتاری نوسانی با وابستگی به داده‌های پیشین هستند.

محاسبه میانگین متحرک در پایتون

حال باید طول پنجره را تعریف و مقدار میانگین متحرک را محاسبه کرد:

L = 3

M = np.zeros(20 – L + 1)

for i in range(0, 20 – L + 1):
    M[i] = (S[i] + S[i + 1] + S[i + 2])/L

به این ترتیب، برای این دنباله، میانگین متحرک محاسبه و در M ذخیره می‌شود. باید توجه داشت که برای میانگین متحرکی با طول پنجره L، مقدار میانگین متحرک به ازای $$ L-1$$ داده اول، تعریف نشده است. با اندکی تغییر در کد و بهبود آن، کدها به صورت زیر در می‌آیند:

L = 3
n = np.size(S) - L + 1
M = np.zeros(n)

for i in range(0, n):
    M[i] = np.mean(S[i:i + L])

به این طریق، برنامه سازگاری بیش‌تری خواهد داشت.

تعریف تابع میانگین متحرک در پایتون

حال می‌توان برای محاسبه میانگین متحرک، تابعی را به صورت زیر تعریف کرد. از این تابع می‌توان به دفعات برای محاسبه میانگین متحرک استفاده کرد.

def SMA(S, L):
    n = np.size(S) - L + 1
    M = np.zeros(n)
    for i in range(0, n):
        M[i] = np.mean(S[i:i + L])
    return M

ایجاد و استفاده از چنین توابعی، دارای دو مزیت است:

1. نیازی به تکرار کدها نخواهد بود و به راحتی می‌توان به میزان مورد نیاز عملیات مربوطه را روی داده‌ها پیاده‌سازی کرد.
2. این تابع به گونه‌ای نوشته شده است که وابسته به طول پنجره یا اندازه داده ورودی نباشد و به همین دلیل، همواره به درستی عمل خواهد کرد.

فیلم آموزش میانگین متحرک – تحلیل تکنیکال در بورس و سرمایه گذاری در بازارهای مالی با Moving Average در تم آف

کلیک کنید

استفاده از تابع تعریف شده برای محاسبه میانگین متحرک در پایتون

حال می‌توان از تابع فوق برای محاسبه میانگین متحرک داده‌ها استفاده کرد:

L = 3 # Window Size
M = SMA(S, L) # Simple Moving Average Values

بنابراین، با استفاده از این تابع، میانگین متحرک به راحتی قابل محاسبه است.

تحلیل شیوه رفتار میانگین متحرک

حالا به منظور بررسی شیوه رفتار میانگین متحرک ، مقادیر توابع S و M در یک نمودار به همراه هم استفاده شده‌اند:

plt.style.use('ggplot')
plt.plot(np.arange(1, N+1), S, label = 'Seri Data',
        c = 'b', linewidth = 0.8, marker = 'o', ms = 4, mfc = 'r', mec = 'r')
plt.plot(np.arange(L, N+1), M, label = 'Simple Moving Average (L={})'.format(L),
        c = 'g', linewidth = 1.3)
plt.xlabel('T')
plt.ylabel('Y')
plt.legend()
plt.show()

باید توجه داشت که چون به تعداد $$ L-1$$ عدد از ابتدای میانگین متحرک قابل محاسبه نیست، باید مقادیر X آن از $$L$$ شروع شود. بهتر است در نمودارهایی که میانگین متحرک بر روی داده‌های اصلی رسم می‌شوند، برای نمودار میانگین متحرک، ضخامت بیشتری را اختصاص داد. در نهایت، خروجی به صورت زیر است:

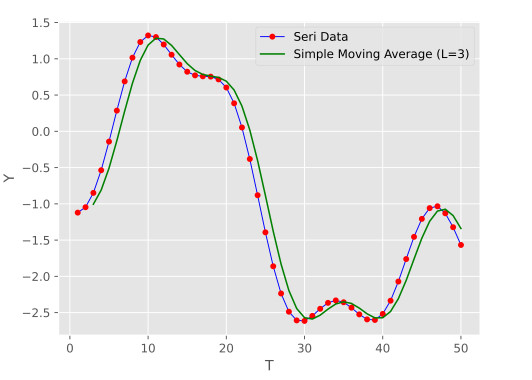
همان‌طور که در تصویر فوق مشاهده می‌شود، میانگین متحرک ، نمودار را با تأخیر دنبال می‌کند.

فیلم آموزش تحلیل و پیش بینی سری های زمانی در تم آف

کلیک کنید

تحلیل اثر طول پنجره در نمودار

می‌توان برای بررسی اثر طول پنجره در نمودار، میانگین متحرک‌هایی با طول 21, 8, 3 را محاسبه و رسم کرد:

M3 = SMA(S, 3) # SMA(3)
M8 = SMA(S, 8) # SMA(8)
M21 = SMA(S, 21) # SMA(21

پس از محاسبه، برای رسم نمودار باید از کدهای زیر استفاده شود:

plt.style.use('ggplot')
plt.plot(np.arange(1, N+1), S, label = 'Seri Data',
        c = 'k', linewidth = 0.8, marker = 'o', ms = 4,
        mfc = 'crimson',mec = 'crimson')
plt.plot(np.arange(3, N+1), M3, label = 'SMA (L=3)',
        linewidth = 1.3, c = 'teal')
plt.plot(np.arange(8, N+1), M8, label = 'SMA (L=8)',
        linewidth = 1.3, c = 'salmon')
plt.plot(np.arange(21, N+1), M21, label = 'SMA (L=21)',
        linewidth = 1.3, c = 'navy')
plt.xlabel('T')
plt.ylabel('Y')
plt.legend()
plt.show()

با اجرای کدهای فوق، خروجی به صورت زیر خواهد بود:

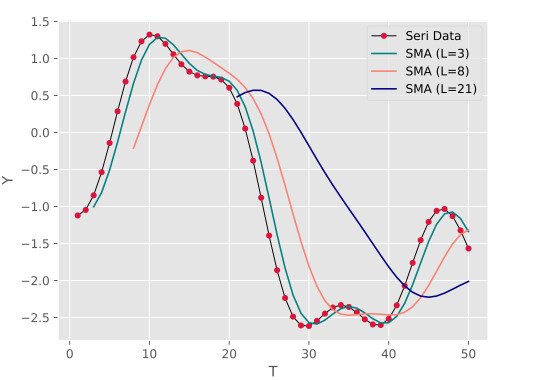
به این ترتیب، همان‌طور که قابل ملاحظه است، با افزایش طول پنجره، سرعت واکنش و شدت واکنش کاهش پیدا می‌کند و همزمان اعتبار و تأخیر افزایش می‌یابند. به همین دلیل، باید در تنظیم طول پنجره میانگین متحرک دقت کرد تا هم اعتبار روند مساعد باشد و هم تاخیر میانگین متحرک به قدری نباشد که مشکل یا خطای بیش از حد ایجاد کند.

فیلم آموزش تحلیل و پیش بینی سری های زمانی در تم آف

کلیک کنید

حذف روند از سری زمانی

می‌توان برای حذف روند از سری زمانی، مقدار میانگین متحرک را از مقدار داده واقعی کم کرد تا مقادیر جدیدی به دست آیند که فاقد روند هستند:

کد مربوطه به صورت زیر است:

D = S[2:] - M3 # Detrended Data With SMA(3)

حالا برای رسم نمودار باید از کدهای زیر استفاده کرد:

plt.style.use('ggplot')
plt.subplot(2,1,1)
plt.plot(np.arange(1, N+1), S, label = 'Seri Data',
        c = 'k', linewidth = 0.8, marker = 'o', ms = 4,
        mfc = 'crimson',mec = 'crimson')
plt.plot(np.arange(3, N+1), M3, label = 'SMA (L=3)',
        linewidth = 1.3, c = 'teal')
plt.xlim(0,N+1)
plt.xlabel('T')
plt.ylabel('Y')
plt.legend()

plt.subplot(2,1,2)
plt.plot(np.arange(3, N+1), D, label = 'Deternded Data With SMA (L=3)',
        linewidth = 1.3, c = 'teal')
plt.plot([3, N], [0, 0], label = 'Zero Line',
        linewidth = 1.3, c = 'k')
plt.xlim(0,N+1)
plt.xlabel('T')
plt.ylabel('Y')
plt.legend()
plt.show()

باید توجه داشت که در زمان استفاده از subplot،‌ اولین آرگومان، تعداد سطرها، دومین آرگومان تعداد ستون‌ها و آخرین آرگومان نیز شماره نمودار مورد نظر را تعیین می‌کند. همچنین، برای هر subplot باید به صورت جداگانه خصیصه‌های xlablel ،ylable ،legend و xlim را تعریف کرد. در آخر، حاصل اجرای کدهای فوق به صورت زیر است:

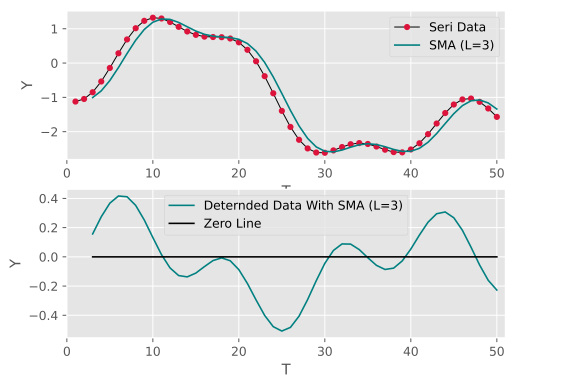
تحلیل حذف روند از سری زمانی

در خروجی فوق مشاهده می‌شود که بخش عمده روند در داده حذف شده است. در نمودار پایین هنگامی که مقدار با خط صفر برخورد می‌کند، همزمان در نمودار بالایی نیز مقدار داده با مقدار میانگین متحرک تلاقی دارد. از طرفی، باید به این نکته نیز توجه داشت که در نمودار پایینی، اثر کمتری از افزایش و کاهش‌های Sharp دیده می‌شود. می‌توان گفت، میانگین متحرک به نوعی مانند فیلتر عمل می‌کند. برای مثال در بازه $$ [15 , 20] $$ و یا در بازه $$ [30 , 40] $$ نوسان خیلی کمی در داده‌های اصلی مشاهده می‌شود، اما در نمودار پایینی، نوسان داده برای این بازه‌ها به خوبی قابل مشاهده است.

فیلم آموزش تحلیل و پیش بینی سری های زمانی در تم آف

کلیک کنید

نکته دیگری که در مورد این نمودار وجود دارد، شباهت نمودار پایینی به مشتق نمودار اصلی است. به طوری که، در هر نقطه که نمودار پایینی مقدار صفر را به خود گرفته است، داده‌های اصلی نیز تقریباً بدون تغییر بوده‌اند. همچنین برای مقادیر مثبت، رشد و برای مقادیر منفی نیز ریزش مشاهده می‌شود. نکته‌ دیگری که در مورد این نمودار وجود دارد، شباهت نمودار پایینی به مشتق نمودار اصلی است. به طوری که، در هر نقطه‌ای که نمودار پایینی مقدار صفر را به خود گرفته، داده‌های اصلی نیز تقریباً بدون تغییر هستند. همچنین، برای مقادیر مثبت در نمودار پایینی رشد و برای مقادیر منفی در نمودار بالایی ریزش اتفاق افتاده است.

جمع‌بندی

دو بخش اصلی در مقاله «میانگین متحرک چیست» ارائه شده است. در بخش ابتدایی مفاهیم نظری و ریاضی پیرامون میانگین متحرک شرح داده شدند و در بخش بعدی، پیاده‌سازی آن در پایتون آموزش داده شد.

فیلم مجموعه آموزش پیش‌‌ بینی و تحلیل سری‌‌ های زمانی در تم آف

کلیک کنید

آموزش پیاده‌سازی میانگین متحرک در پایتون به صورت گام به گام و به همراه کدها و تصاویر خروجی ارائه شده‌اند. توصیه می‌کنیم بعد از این مطلب به سراغ مطالعه مطلب پیاده سازی میانگین متحرک نمایی در پایتون بروید.