میانگین متحرک نمایی دوگانه و سه گانه در پایتون — راهنمای گام به گام

در مطالب پیشین مجله تم آف، به صورت گام به گام به پیاده سازی میانگین متحرک نمایی پرداختیم و مشاهده کردیم که از تأخیر کمتری نسبت به میانگین متحرک ساده دارد. در این مطلب میخواهیم به میانگین متحرک نمایی دوگانه (Double Exponential Moving Average – DEMA) و میانگین متحرک نمایی سهگانه (Triple Exponential Moving Average – TEMA) بپردازیم. در این نوع از میانگین متحرکها، مشکل تأخیر موجود در میانگین متحرک نمایی کمتر شده است.

میانگین متحرک نمایی دوگانه
اگر یک سری زمانی با نماد $$X$$ داشته باشیم، میتوانیم میانگین متحرک نمایی با طول بازه $$L$$ را بهصورت زیر تعریف کنیم:
$$ E=text{EMA}(X,L) $$
حال میتوانیم میانگین متحرک دیگری روی $$E$$ محاسبه کنیم:
$$EoE=text{EMA}(E,L)$$
براساس تجربه میدانیم که $$E$$ نسبت به $$X$$ تأخیر دارد و $$EoE$$ نیز نسبت به $$X$$ دارای تأخیر دوچندان است. براساس این موضوع، میتوان تقریباً گفت که فاصله $$E$$ از مقداری که باید باشد (Target)، با فاصله $$EoE$$ از $$E$$ برابر است، یعنی:
$$T-Econg E-EoE$$
در رابطه فوق، مقدار $$T$$ برابر با عددی است که در صورت نبود تأخیر آن را خواهیم داشت. حال پس از حل رابطه بهفرم زیر میرسیم:
$$ Tcong 2E-EoE $$
به این ترتیب، میانگین متحرک نمایی دوگانه تعریف میشود:
$$text{DEMA}=2text{EMA}(X,L)-text{EMA}(text{EMA}(X,L),L)=2E-EoE$$
به این ترتیب، فرمول نهایی حاصل میشود.
میانگین متحرک نمایی سه گانه
در این حالت نیز مشابه میانگین متحرک نمایی دوگانه تعریف میکنیم:
$$begin{aligned}
E&=text{EMA}(X, L)\
E o E&=text{EMA}(E, L)\
E o E o E&=text{EMA}(E o E, L)
end{aligned}$$
براساس آنچه گفته شد، تأخیر بین این موارد بهشکل زیر خواهد بود:
$$X
اگر یک تقریب بهصورت زیر داشته باشیم:
$$T-E cong E-E o E cong E o E-E o E o E=Delta$$
میتوان نوشت:
$$T-E o E o E cong(T-E)+(E-E o E)+(E o E-E o E o E)=3 Delta $$
حال اگر مقدار $$Delta$$ را برحسب میانگین متحرک اول و دوم بنویسیم، خواهیم داشت:
$$T-E o E o E cong 3(E-E o E)=3 E-3 E o E$$
اکنون میانگین متحرک نمایی سهگانه را تعریف میکنیم:
$$
begin{aligned}
text{TEMA}&=3text{EMA}(X,L)-3text{EMA}(text{EMA}(X,L),L)+text{EMA}(text{EMA}(text{EMA}(X,L),L),L)\&=3E-3EoE+EoEoE
end{aligned}
$$
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
پیاده سازی میانگین متحرک نمایی دوگانه و سه گانه در پایتون
مباحث مربوط به تعریف میانگین متحرکها بیان شد. حال میتوانیم وارد محیط برنامهنویسی شده و کتابخانههای مورد نیاز را فراخوانی کنیم:
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as pltاین کتابخانهها بهترتیب برای موارد زیر استفاده خواهند شد:
- محاسبات برداری و کار با آرایهها
- کار با دیتافریمها و مجموعه داده
- دریافت آنلاین دادههای مربوط به قیمت نمادها
- رسم نمودار
حال، تنظیمات مربوط به نمودارها را بهصورت زیر وارد میکنیم:
plt.style.use('ggplot')سپس نماد مورد نظر را که قیمت نقره است را تعریف و تاریخچه قیمت برای یک سال بین ۲۰۲۱ تا ۲۰۲۲ دریافت میکنیم:
Ticker = yf.Ticker('AG')
DF = Ticker.history(interval='1d', start='2021-01-01', end='2022-01-01')به این ترتیب، دیتافریم قیمت دریافت میشود. حال ۵ سطر اول مجموعه داده را مشاهده میکنیم:
print(DF.head(5))که خواهیم داشت:
Open High Low Close Volume Dividends Stock Splits Date 2020-12-31 13.644106 13.714025 13.314491 13.424362 5240600 0.0 0 2021-01-04 14.123548 14.543059 13.963733 14.223431 10227500 0.0 0 2021-01-05 14.273373 14.273373 13.793932 14.243408 8188200 0.0 0 2021-01-06 14.133536 14.223431 13.644106 14.213443 7572700 0.0 0 2021-01-07 14.093582 14.323315 13.783943 13.993699 5674700 0.0 0
به این ترتیب، داده حاصل میشود. حال ستون مربوط به قیمت Close را به شکل یک آرایه در میآوریم:
S = DF['Close'].to_numpy()برای رسم نمودار سری زمانی مینویسیم:
plt.semilogy(S, lw=0.9, c='crimson')
plt.title('Silver 1 Year Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.show()
که شکل زیر را خواهیم داشت.
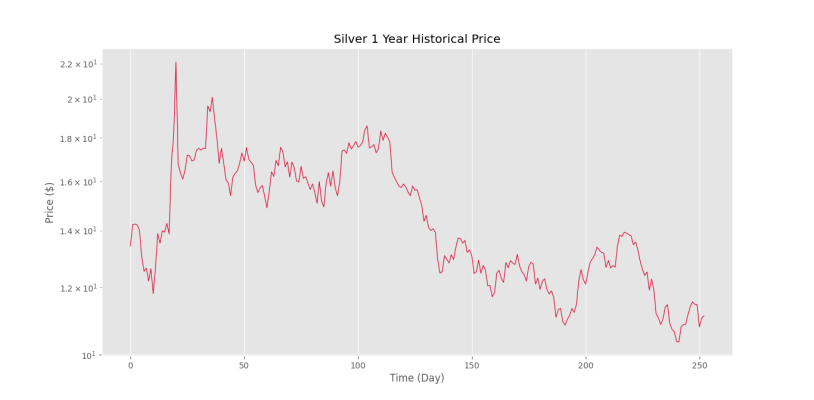
به این ترتیب، «نمودار نیمهلگاریتمی» (Semi-Logarithm) رسم میشود.
حال، کد مربوط به تابع میانگین متحرک نمایی را وارد کد میکنیم:
def EMA(S:np.ndarray, L:int, r:float=1):
a = (1 + r) / (L + r)
nD0 = S.size
nD = nD0 - L + 1
M = np.zeros(nD)
M[0] = np.mean(S[:L])
for i in range(1, nD):
M[i] = a * S[i+L-1] + (1-a) * M[i-1]
return Mاکنون میتوانیم با استفاده از از این تابع، تابعی برای DEMA پیادهسازی کنیم. این تابع در ورودی سری زمانی اولیه و طول میانگینگیری را میگیرد:
def DEMA(S:np.ndarray, L:int):حال میتوانیم میانگین متحرکهای مراتب اول و دوم را محاسبه کنیم:
def DEMA(S:np.ndarray, L:int):
E = EMA(S, L)
EoE = EMA(E, L)حال میتوانیم اندازه خروجی را محاسبه کنیم که برابر با $$EoE$$ خواهد بود:
def DEMA(S:np.ndarray, L:int):
E = EMA(S, L)
EoE = EMA(E, L)
nD = EoE.sizeبا توجه به اینکه طول آرایه $$E$$ بیشتر از $$nD$$ است، از آرایه $$E$$ تنها $$nD$$ عضو انتهایی را نگه میداریم:
def DEMA(S:np.ndarray, L:int):
E = EMA(S, L)
EoE = EMA(E, L)
nD = EoE.size
E = E[-nD:]حال میتوانیم خروجی را محاسبه کرده و برگردانیم:
def DEMA(S:np.ndarray, L:int):
E = EMA(S, L)
EoE = EMA(E, L)
nD = EoE.size
E = E[-nD:]
dema = 2*E - EoE
return demaبه این ترتیب، تابع پیادهسازی میشود.
حال، میانگین متحرک نمایی و میانگین متحرک نمایی دوگانه سری را محاسبه میکنیم:
ema = EMA(S, 15)
dema = DEMA(S, 15)حال روی نمودار هر دو را رسم میکنیم و نمایش میدهیم:
T = np.arange(S.size)
plt.semilogy(T, S, lw=0.9, c='crimson', label='Price')
plt.semilogy(T[-ema.size:], ema, lw=0.9, c='teal', lable='EMA(15)')
plt.semilogy(T[-dema.size:], dema, lw=0.9, c='k', lable='DEMA(15)')
plt.title('Silver 1 Year Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()که شکل زیر را خواهیم داشت.
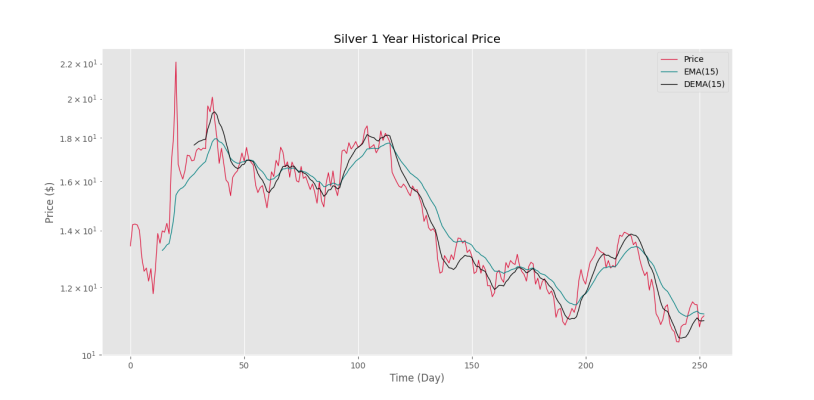
به این ترتیب، مشاهده میکنیم که میانگین متحرک نمایی سهگانه، رفتار بهتری دارد و سریعتر از میانگین متحرک نمایی ساده واکنش نشان میدهد. علاوه بر واکنش سریعتر، نقاط حمایت و مقاومت را بهتر و دقیقتر نشان میدهد.
حال تابعی دیگر برای پیادهسازی میانگین متحرک نمایی سهگانه ایجاد میکنیم:
def TEMA(S:np.ndarray, L:int):سپس میانگین متحرک نمایی مراتب اول، دوم و سوم را محاسبه میکنیم:
def TEMA(S:np.ndarray, L:int):
E = EMA(S, L)
EoE = EMA(E, L)
EoEoE = EMA(EoE, L)حال اندازه خروجی را محاسبه کرده، آرایههای $$E$$ و $$EoE$$ را اصلاح و خروجی را محاسبه میکنیم:
def TEMA(S:np.ndarray, L:int):
E = EMA(S, L)
EoE = EMA(E, L)
EoEoE = EMA(EoE, L)
nD = EoEoE.size
E = E[-nD:]
EoE = EoE[-nD:]
tema = 3*E - 3*EoE + EoEoE
return temaبه این ترتیب، تابع پیادهسازی میشود. به شیوه مشابه از هر سه تابع خروجی میگیریم:
ema = EMA(S, 15)
dema = DEMA(S, 15)
tema = TEMA(S, 15)برای رسم نمودار مینویسیم:
T = np.arange(S.size)
plt.semilogy(T, S, lw=0.9, c='crimson', label='Price')
plt.semilogy(T[-ema.size:], ema, lw=0.9, c='teal', label='EMA(15)')
plt.semilogy(T[-dema.size:], dema, lw=0.9, c='k', label='DEMA(15)')
plt.semilogy(T[-tema.size:], tema, lw=0.9, c='k', label='TEMA(15)')
plt.title('Silver 1 Year Historical Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()که در خروجی شکل زیر را خواهیم داشت.
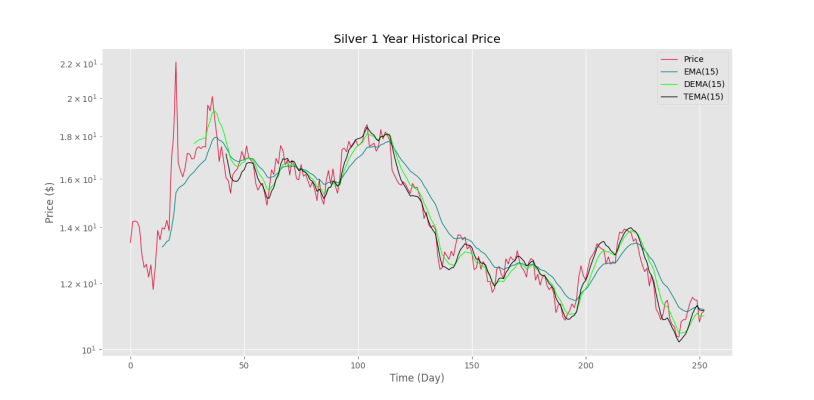
مشاهده میکنیم که واکنش میانگین متحرک نمایی سهگانه نیز بهتر از میانگین متحرک نمایی دوگانه است.
جمعبندی
در این مطلب، میانگین متحرک نمایی دوگانه و سهگانه را بررسی و پیادهسازی کردیم.
برای مطالعه بیشتر، میتوان موارد زیر را بررسی کرد:
- نمودار قیمت، $$E$$ و $$EoE$$ و $$EoEoE$$ را رسم کرده و آنها را با هم مقایسه کنید.
- آیا میتوان میانگین متحرک نمایی سهگانه را به شیوهای دیگر نیز محاسبه کرد؟
- میانگین متحرک نمایی چهارگانه را پیادهسازی کنید.
- در $$L$$های مختلف، نمودار مقایسه نهایی را رسم کرده و بهترین $$L$$ را پیدا کنید.
مطلبی که در بالا مطالعه کردید بخشی از مجموعه مطالب «آموزش پیادهسازی انواع میانگین های متحرک در پایتون» است. در ادامه، میتوانید فهرست این مطالب را ببینید:
- میانگین متحرک چیست؟ + پیاده سازی Moving Average در پایتون
- پیاده سازی میانگین متحرک نمایی در پایتون — راهنمای گام به گام
- میانگین متحرک نمایی دوگانه و سه گانه در پایتون — راهنمای گام به گام(همین مطلب)
- میانگین متحرک وزن دار در پایتون — راهنمای گام به گام
- پیاده سازی میانگین متحرک هال در پایتون — راهنمای گام به گام

