ضریب همبستگی غیرخطی چترجی (Chatterjee) در پایتون — راهنمای گام به گام

در آموزشهای پیشین مجله تم آف، با پیادهسازی الگوریتم گرادیان کاهشی و روش نیوتون رافسون در پایتون آشنا شدیم. در این آموزش، مطالبی را درباره پیادهسازی ضریب همبستگی چترجی در پایتون بیان میکنیم.

آشنایی با ضریب همبستگی غیرخطی چترجی (Chatterjee)
ضریب همبستگی معیاری برای بررسی ارتباط آماری بین دو متغیر است. با استفاده از این عدد میتوان دریافت که آیا ارتباط معناداری بین دو متغیر وجود دارد یا خیر. از همبستگی میتوان برای آمادهسازی داده، کاهش ابعاد، تحلیل گراف و… استفاده کرد.
برای انواع مختلفی از متغیرها، معیارهای متفاوتی تعریف شده است که پرتکرارترین حالت مربوط به بررسی همبستگی بین دو متغیر پیوسته است.
ضریب همبستگی پیرسون (Pearson Correlation Coefficient) پرکاربردترین معیار برای بررسی همبستگی خطی بین متغیرها است که بهصورت زیر محاسبه میشود:
$$ large r{(X, Y)}=frac{operatorname{cov}{(X, Y)}}{operatorname{var}{(X)} cdot operatorname{var}{(Y)}}=frac{sumleft(x_{i}-bar{x}right)left(y_{i}-bar{y}right)}{sqrt{sumleft(x_{i}-bar{x}right)^{2} sumleft(y_{i}-bar{y}right)^{2}}} $$
رابطه فوق همواره عددی بین $$-1$$ و $$+1$$ خواهد داد. مشکل بزرگی که این معیار دارد، خطی بودن آن است و سایر ارتباطات بین متغیرها را نمیتواند تشخیص دهد. به همین دلیل، اغلب از Scatter Pair Plot برای بررسی ارتباطات غیرخطی بین متغیرها استفاده میشود.
روش جدید دیگر برای بررسی همبستگیهای غیرخطی، استفاده از ضریب همبستگی رتبهای چترجی (Chatterjee Rank Correlation) است. این ضریب نیز همواره عددی بین $$-1$$ و $$+1$$ را به خود میگیرد، با این تفاوت که قابلیت کشف ارتباطات غیرخطی (درجه دوم، لگاریتمی، سینوسی و…) را نیز دارد.
برای محاسبه ضریب همبستگی رتبهای چترجی دو متغیر پیوسته با مقادیر غیرتکراری در $$X$$، بهصورت زیر عمل میکنیم:
$$ large xi{(X, Y)}=1-frac{3 sum_{i=1}^{n-1}left|r_{i+1}-r_{i}right|}{n^{2}-1} $$
در این رابطه، $$r$$ نشان دهنده Rank مربوط به $$Y$$ها بعد از مرتب شدن با توجه به $$X$$ها است.
نکته دیگری که وجود دارد، این است که بهازای $$n$$ داده، در شدیدترین حالت همبستگی، مقدار ضریب برابر با عبارت زیر خواهد بود:
$$ large frac{ n-2}{n+1}$$
که با زیاد شدن تعدادها، قابل صرفنظر خواهد بود.
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
ضریب همبستگی غیرخطی چترجی (Chatterjee) در پایتون
حال برای بررسی و پیادهسازی ضریب همبستگی چترجی در پایتون، وارد محیط برنامهنویسی شده و کتابخانههای مورد نیاز را فراخوانی میکنیم:
import numpy as np
import matplotlib.pyplot as pltابتدا Random State و Style را تنظیم میکنیم:
np.random.seed(0)
plt.style.use('ggplot')حال باید ضریب همبستگی پیرسون را پیادهسازی کنیم. برای این کار، ابتدا یک تابع تعریف میکنیم که در ورودی دو آرایه مربوط به متغیرها را دریافت میکند:
def PCC(X:np.ndarray, Y:np.ndarray):حال برای محاسبه کوواریانس خواهیم داشت:
def PCC(X:np.ndarray, Y:np.ndarray):
C = np.cov(X, Y)ماتریس $$C$$ در این شرایط بهشکل زیر خواهد بود:
$$ large left[begin{array}{cc}
operatorname{var}{(X)} & operatorname{cov}{(X, Y)} \
operatorname{cov}{(X, Y)} & operatorname{var}{(Y)}
end{array}right] $$
بنابراین، میتوان از آن بهصورت زیر برای محاسبه ضریب همبستگی پیرسون استفاده کرد:
def PCC(X:np.ndarray, Y:np.ndarray):
C = np.cov(X, Y)
pcc = C[0, 1] / (C[0, 0] * C[1, 1])**0.5
return pccاین تابع، در خروجی، ضریب مورد نظر را برمیگرداند.
توجه داشته باشید که میتوان از کتابخانه Scipy نیز برای محاسبه ضریب همبستگی پیرسون استفاده کرد:
pcc = scipy.stats.pearsonr(X, Y)[0]حال برای بررسی عملکرد کد، یک مجموعه داده با رابطه زیر تولید میکنیم:
$$ large y _ i = 2 x _ i + 1 + e_i , ;;;;;; sigma^2(e) =0.5, ;; overline{e}=0 $$
X = np.random.uniform(-5, +5, 50)
Y = 2*X + 1 + np.random.normal(0, 0.5, 50)که برای رسم این دو متغیر در مقابل هم، مینویسیم:
plt.scatter(X, Y, s=12)
plt.xlabel('X')
plt.ylabel('Y')
plt.axhline(lw=1, c='k')
plt.axvline(lw=1, c='k')
plt.show()که نمودار زیر حاصل میشود.
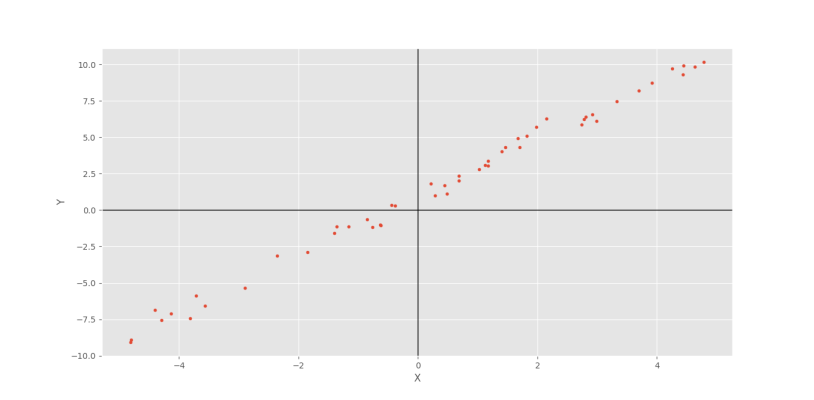
حال برای محاسبه و مشاهده ضریب همبستگی پیرسون مینویسیم:
pcc = PCC(X, Y)
print(f'Pearson Correlation Coefficient: {pcc}')که خواهیم داشت:
Pearson Correlation Coefficient: 0.9963573476843708
حال اگر مقدار واریانس نویز اضافهشده به متغیر $$Y$$ را از $$0.5$$ به $$2$$ تغییر دهیم، شکل زیر را خواهیم داشت.
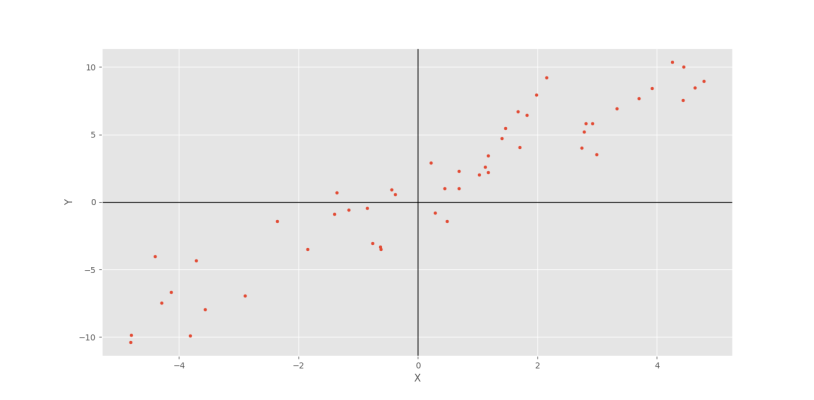
در این شرایط، ضریب همبستگی پیرسون نیز از $$0.99$$ به $$0.94$$ کاهش مییابد.
حال رابطه استفادهشده در تولید دادهها را بهصورت زیر تغییر میدهیم:
$$ large y _ i = x _ i ^2+1+ e_i , ;;;;;; sigma^2(e) =0.5, ;; overline{e}=0 $$
در این حالت نمودار زیر حاصل خواهد شد.
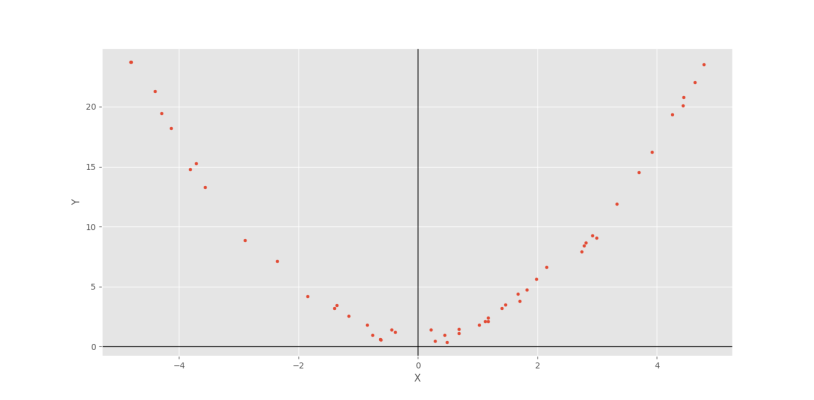
در این نمودار با اینکه ارتباط بین $$X$$ و $$Y$$ کاملاً مشهود است، ضریب همبستگی پیرسون عدد $$-0.03$$ را به خود میگیرد. به دلیل این مشکل، نیاز به معیارهایی که بتواند روابط غیرخطی را تشخیص دهد، افزایش مییابد.
پیادهسازی ضریب همبستگی رتبهای چترجی در پایتون
حال به سراغ ضریب همبستگی رتبهای چترجی میرویم تا آن را نیز پیادهسازی کرده و نتایج را مشاهده کنیم.
ابتدا یک تابع تعریف کرده و متغیرهای ورودی را دریافت میکنیم:
def CRC(X:np.ndarray, Y:np.ndarray):حال باید اندیسهای دادهها را با توجه به ترتیب $$X$$ محاسبه کنیم:
def CRC(X:np.ndarray, Y:np.ndarray):
A = np.argsort(X)حال میتوانیم ماتریس $$Y$$ را با استفاده از ماتریس $$A$$ مرتب کنیم:
def CRC(X:np.ndarray, Y:np.ndarray):
A = np.argsort(X)
Ys = Y[A]حال میتوانیم ماترس Rank را تولید کنیم، در این ماتریس، هر عضو از دادهها با تک تک اعضای دیگر مقایسه میشود و بزرگتر یا کوچکتر بودن آن نشان داده میشود. برای این کار میتوانیم بنویسیم:
def CRC(X:np.ndarray, Y:np.ndarray):
A = np.argsort(X)
Ys = Y[A]
R = (Ys[:, None] به این ترتیب، ماتریس مربعی $$R$$ تولید میشود. در شکل نهایی رابطه، تنها نیاز به تعداد Trueها در هر ستون داریم، بنابراین باید در طول ستونها عمل جمع (Summation) انجام دهیم:
A = np.argsort(X)
Ys = Y[A]
R = (Ys[:, None] حال تعداد دادهها را نیز محاسبه کرده و در فرمول آورده شده قرار میدهیم:
def CRC(X:np.ndarray, Y:np.ndarray):
A = np.argsort(X)
Ys = Y[A]
R = (Ys[:, None] به این ترتیب، ضریب همبستگی رتبهای چترجی محاسبه و در خروجی برگردانده میشود.
حال مجموعه داده مربوط به رابطه سهمی را تولید کرده و ضریب همبستگی رتبهای چترجی را محاسبه میکنیم:
X = np.random.uniform(-5, +5, 50)
Y = X**2 + 1 + np.random.normal(0, 0.5, 50)
pcc = PCC(X, Y)
crc = CRC(X, Y)
print(f'Pearson Correlation Coefficient: {pcc}')
print(f'Chatterjee Rank Correlation: {crc}')
plt.scatter(X, Y, s=12)
plt.xlabel('X')
plt.ylabel('Y')
plt.axhline(lw=1, c='k')
plt.axvline(lw=1, c='k')
plt.show()
که شکل زیر را خواهیم داشت.
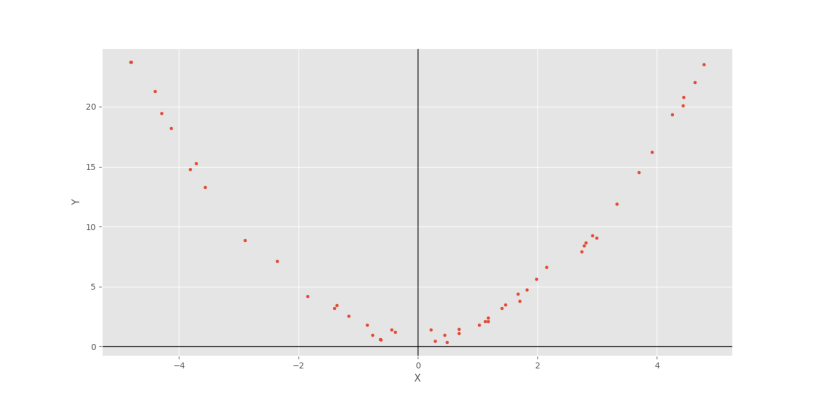
Pearson Correlation Coefficient: -0.03724899705945379 Chatterjee Rank Correlation: +0.82953181272509
به این ترتیب، مشاهده میکنیم که ضریب همبستگی رتبهای چترجی وجود ارتباطی آماری بین دو متغیر را تأیید میکند.
میتوان ارتباطات پیچیدهتر مثل ترکیب دو تابع سینوسی را نظر گرفت:
X = np.random.uniform(-5, +5, 100)
Y = 0.5 * np.sin(2*X + 1) + 1.2 * np.sin(X) + np.random.normal(0, 0.1, 100)که در این حالت نتایج مطابق شکل زیر خواهد بود.
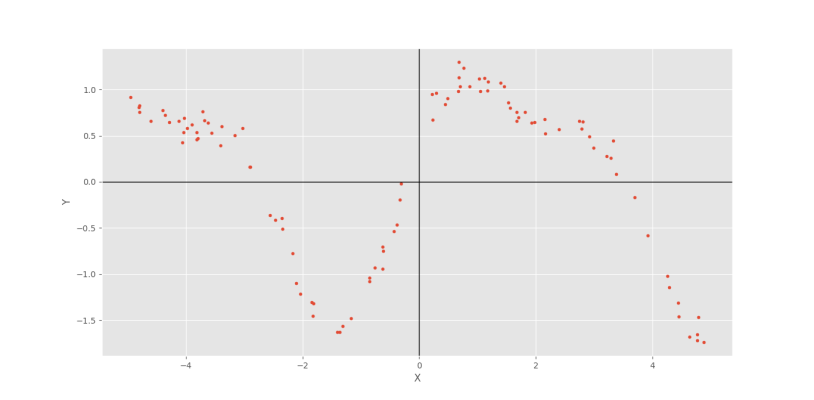
Pearson Correlation Coefficient: -0.2120912310052988 Chatterjee Rank Correlation: +0.786978697869787
به این ترتیب، عملکرد مناسب ضریب همبستگی رتبهای چترجی مشهود است.
جمعبندی
در این آموزش، با پیادهسازی ضریب همبستگی غیرخطی Chatterjee در پایتون بهصورت گام به گام آشنا شدیم. برای بررسیهای بیشتر میتوان ضرایب مشابه را با ضریب همبستگی رتبهای چترجی مقایسه کرد:
- ضریب همبستگی رتبهای اسپیرمن (Spearman Rank Correlation Coefficient)
- ضریب همبستگی رتبهای کندال (Kendall Rank Correlation Coefficient)

