حذف نویز از تصاویر با شبکه های عصبی خودرمزگذار یا Autoencoder

در مطلب گذشته، به پیادهسازی شبکه عصبی پرسپترون یک لایه (Sigle Layer Perceptron یا SLP) پرداختیم. در این مطلب قصد داریم یک شبکه عصبی خودرمزگذار (Autoencoder) پیادهسازی کنیم، سپس با استفاده از آن، حذف نویز از تصاویر با شبکه های عصبی خودرمزگذار را داشته باشیم.

شبکه خودرمزگذار چیست؟
نوع به خصوصی از شبکههای عصبی هستند که از دو بخش «رمزگذار» (Encoder) و «رمزگشا» (Decoder) ساخته شدهاند. در اغلب موارد شبکه در جهتی آموزش داده میشود که ورودی دریافت شده یا نمونه بسیار مشابه آن را در خروجی برگرداند. این بخش رمزگذار با دریافت ورودی، اغلب اطلاعات (Information) و ویژگیهای (Feature) مهم را استخراج کرده و با ابعاد کمتری به شبکه رمزگشا میدهد.
با توجه به اینکه مدل مجبور است بیشترین اطلاعات ممکن را از گلوگاه (Bottleneck) منتقل کند، سعی میکند در بخش رمزگذار، بر روی ویژگیهای عمده و مهم تمرکز کند. این امر باعث میشود نویزها نتوانند از گلوگاه عبور کنند. مدل رمزگشا نیز سعی میکند با دریافت ویژگیهایی که شبکه رمزگذار تولید کرده، ورودی اولیه را بازسازی کند و برگرداند. به طور کلی اگر ورودی شبکه را با x و خروجی شبکه را با نام y یا $$x^ prime$$ بشناسیم، رابطه زیر را خواهیم داشت:
$$z=f(x)$$
در این رابطه z اطلاعات خروجی از شبکه رمزگذار است و f نشاندهنده تابع معادل با شبکه رمزگذار است.
شبکه رمزگشا با دریافت همان اطلاعات خروجی نهایی را تولید میکند:
$$
x^{prime}=g(z)
$$
در این رابطه نیز تابع g معادل شبکه رمزگشا است. به طور کلی خواهیم داشت:
$$
x^{prime}=g(z)=g(f(x))=g circ f(x)
$$
با اینکه میتوان gof را به عنوان یک تابع یکپارچه تعریف کرد اما به دو دلیل زیر ترجیح بر این است که جدا در نظر گرفته شوند:
- تاکید بر الزامی بودن گلوگاه
- نیاز به استفاده از شبکه رمزگذار به تنهایی برای برخی اهداف
در این مطلب قصد داریم یک تصویر را با استفاده از نویز تصادفی مخدوش کنیم و وارد شبکه عصبی خودرمزگذار کنیم تا در خروجی تصویر اولیه را برای ما تولید کند. در تصویر زیر یک عکس اولیه آمده و در کنار آن همان تصویر با نویز تصادفی آورده شده:
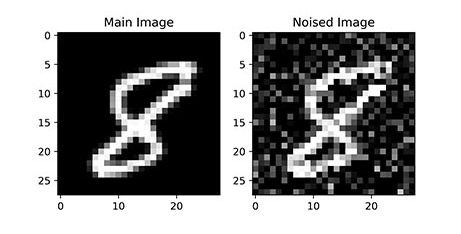
بنابراین نیاز به یک مجموعه داده (Dataset) تصویری داریم. به این منظور از مجموعه داده MNIST یا Modified National Institute of Standards and Technology استفاده خواهیم کرد که شامل ارقام دستنویس است و در اندازه و نسخههای مختلفی وجود دارد.
دانلود کد آماده برای حذف نویز از تصاویر با شبکه های عصبی خودرمزگذار
با توجه به پیچیدگی مراحل گفته شده و امکان بروز خطا در کپی کردن کدها، کد اصلی در قالب یک فایل تهیه شده که با استفاده از لینک زیر میتوانید آن را دانلود کنید.
- برای دانلود کد آماده برای حذف نویز از تصاویر با شبکه های عصبی خودرمزگذار + اینجا کلیک کنید.
پیادهسازی شبکه عصبی خودرمزگذار
در ابتدای کد، کتابخانههای مورد نیاز را فراخوانی میکنیم:
import os as os
import numpy as np
import random as ran
import typing as typ
import tensorflow as tf
import keras.utils as ut
import keras.layers as lay
import keras.models as mod
import keras.losses as los
import keras.datasets as dt
import keras.optimizers as opt
import matplotlib.pyplot as plt
import keras.activations as act
import sklearn.model_selection as ms
این موارد به ترتیب برای موارد زیر استفاده خواهند شد:
- تعیین Seed مربوط به Hash پایتون
- محاسبات برداری برای روی داده و نتایج
- تولید اعداد تصادفی
- تعیین جنس برخی ورودیهای خاص توابع
- ایجاد و آموزش شبکه عصبی
- ذخیره ساختار شبکه عصبی ایجاد شده
- لایههای Keras برای ایجاد شبکه عصبی
- مدلهای Keras برای ایجاد شی اولیه
- خطاهای Keras برای تعیین خطای مورد استفاده در آموزش شبکه عصبی
- مجموعه دادههای Keras برای دسترسی به مجموعه داده MNIST
- بهینهسازهای Keras برای تعیین بهینهساز مورد استفاده در آموزش شبکه عصبی
- رسم نمودار نتایج و تصاویر
- توابع فعالسازی Keras برای تعیین تابع فعالساز برخی لایههای شبکه عصبی
- تقسیم مجموعه داده
به منظور پیادهسازی شبکه عصبی خودرمزگذار، از مفهوم کلاس و برنامهنویسی شیگرا (Object-Oriented Programming) در پایتون استفاده خواهیم کرد. بنابراین یک کلاس با نام AEDN که مخفف Autoencoder Denoiser است ایجاد میکنیم:
class AEDN:متد سازنده
حال در اولین گام، متد (Method) سازنده را ایجاد میکنیم. این متد در ورودی لیست (List) تعداد فیلترهای (Filter) لایههای پیچشی (Convolution) و Random State را دریافت خواهد کرد:
def __init__(self,
nConvolution:list[int],
RandomState:typ.Union[int, None]=None):
توجه داشته باشید که nConvolution یک لیست است و اعضای آن باید اعداد صحیح یا Integer باشند. ورودی RandomState مقدار پیشفرض None را گرفته است که نشان میدهد در صورت عدم تعریف آن، Randomness مدل باقی خواهد ماند. با توجه به اینکه این ورودی هم میتواند یک عدد صحیح باشد و هم None باشد، با استفاده از typing.Union یک مجموعه از جنسهای قابل قبول برای این ورودی را تعریف میکنیم. پس از دریافت این ورودیها، آنها را به ترتیب در شی ذخیره میکنیم:
def __init__(self,
nConvolution:list[int],
RandomState:typ.Union[int, None]=None):
self.nConvolution = nConvolution
self.RandomState = RandomState
همانطور که گفتیم، شبکه خودرمزگذار دارای دو بخش رمزگذار و رمزگشا است. با توجه به اینکه میخواهیم بر روی مجموعه داده تصویری کار کنیم، شبکههای عصبی پیچشی (Convolutional Neural Networks) گزینه مناسبی هستند. لایههای Convolution دو بُعدی برای شبکه رمزگذار مناسب هستند. در شبکه رمزگشا، با توجه به اینکه عکس فرآیند قبلی رخ میدهد، از لایههای Convolution Transpose دو بُعدی استفاده میشود. نکته مهمی که وجود دارد این است که تعداد فیلترهای شبکه رمزگذار معلوم است. برای شبکه رمزگشا باید همان تعداد فیلتر با ترتیب عکس استفاده شود. بنابراین تعداد این فیلترها را نیز محاسبه و ذخیره میکنیم:
def __init__(self,
nConvolution:list[int],
RandomState:typ.Union[int, None]=None):
self.nConvolution = nConvolution
self.RandomState = RandomState
self.nConvolutionT = nConvolution[::-1]
حال برخی تنظیمات را اعمال میکنیم. در اولین قدم قالب رسم نمودارها را تعیین میکنیم:
def __init__(self,
nConvolution:list[int],
RandomState:typ.Union[int, None]=None):
self.nConvolution = nConvolution
self.RandomState = RandomState
self.nConvolutionT = nConvolution[::-1]
plt.style.use('ggplot')
سپس بررسی میکنیم، اگر Random State ورودی غیر از None باشد، تمامی Seedها را تنظیم میکنیم:
def __init__(self,
nConvolution:list[int],
RandomState:typ.Union[int, None]=None):
self.nConvolution = nConvolution
self.RandomState = RandomState
self.nConvolutionT = nConvolution[::-1]
plt.style.use('ggplot')
if self.RandomState is not None:
ran.seed(self.RandomState)
np.random.seed(self.RandomState)
tf.random.set_seed(self.RandomState)
os.environ['PYTHONHASHSEED'] = str(self.RandomState)
به این ترتیب متد سازنده یا __init__ تکمیل میشود.
متد ایجاد مدل
به متد دیگری نیاز داریم که با دریافت ورودی شبکه، ابعاد آن را استخراج کرده و مدل را ایجاد کند. این متد را به شکل زیر ایجاد میکنیم:
def Create(self,
trX:np.ndarray):
از آرایه trX تنها برای محاسبه ابعاد ورودی شبکه استفاده خواهیم کرد. به این منظور ارتفاع، عرض و تعداد کانالهای تصاویر را استخراج میکنیم:
def Create(self,
trX:np.ndarray):
_, self.h, self.w, self.c = trX.shape
توجه داشته باشید که بُعد اول trX نشاندهنده دادهها است و مهم نیست. حال میتوانیم ابعاد ورودی شبکه را به شکل یک تاپل (Tuple) تعریف کنیم.
def Create(self,
trX:np.ndarray):
_, self.h, self.w, self.c = trX.shape
self.InputShape = (self.h, self.w, self.c)
توجه داشته باشید که ابعاد ورودی و خروجی این شبکه یکسان است.
حال مدل را ایجاد میکنیم. به این منظور از keras.models.Sequential استفاده میکنیم:
def Create(self,
trX:np.ndarray):
_, self.h, self.w, self.c = trX.shape
self.InputShape = (self.h, self.w, self.c)
self.Model = mod.Sequential(name='Autoencoder')
حال یک لایه ورودی به شبکه اضافه میکنیم:
def Create(self,
trX:np.ndarray):
_, self.h, self.w, self.c = trX.shape
self.InputShape = (self.h, self.w, self.c)
self.Model = mod.Sequential(name='Autoencoder')
self.Model.add(lay.InputLayer(input_shape=self.InputShape))
این لایه عملکرد به خصوصی ندارد و تنها برای تعریف ورودی و ابعاد آن کاربرد دارد.
حال میتوانیم لایههای پیچشی را اضافه کنیم. به ازای هر عدد موجود در لیست self.nConvolution یک لایه اضافه میکنیم:
for i in self.nConvolution:
self.Model.add(lay.Conv2D(filters=i,
kernel_size=(3, 3),
padding='same'))
توجه داشته باشید که سایز فیلترها 3×3 در نظر گرفته شده است که در اغلب موارد تنظیمات خوبی است. ورودی padding شیوه برخورد با پیکسلهای (Pixel) موجود در مرز تصویر را نشان میدهد. با توجه به اینکه میخواهیم در خروجی تصویر هماندازه با تصویر ورودی دریافت کنیم، تمامی لایههای پیچشی را با padding=’same’
ایجاد میکنیم.
براساس تجربه به این نتیجه رسیده شده است که اضافه کردن یک لایه Leaky ReLU و Maxpooling میتواند عملکرد شبکه رمزگذار را بهبود بخشد. به این منظور حلقه اخیر را به شکل زیر تغییر میدهیم:
for i in self.nConvolution:
self.Model.add(lay.Conv2D(filters=i,
kernel_size=(3, 3),
padding='same'))
self.Model.add(lay.LeakyReLU(alpha=0.2))
self.Model.add(lay.MaxPooling2D(pool_size=(2, 2),
padding='same'))
تابع فعالسازی Leaky ReLU ضابطهای به شکل زیر دارد:
$$
f(x)=left{begin{array}{c}
x quad x geq 0 \
alpha times x quad x
end{array}right.
$$
ورودی alpha برای لایه Leaky ReLU همان $$alpha$$ را تعیین میکند. این ضریب باعث میشود نورون در هنگام غیرفعال بودن نیز گرادیان تولید کند.
با توجه به اینکه بر روی تصاویر کار میکنیم، لایه Maxpooling2D استفاده میکنیم. ورودی pool_size=(2,2) به این معنی است که این لایه از هر مربع با ابعاد تنها پیکسلی با بیشترین سیگنال را انتخاب و به لایه بعد منتقل میکند. این فرآیند باعث میشود که ابعاد تصویر ورودی در هر دو بعد نصف شود. به این ترتیب با دو بار اعمال این لایه در دو بار تکرار حلقه (اگر دو لایه پیچش در نظر بگیریم)، ابعاد تصویر اولی از 28×28 به 7×7 کاهش یافت. این اتفاق باعث ایجاد حالت گلوگاه برای مدل خواهد شد.
این حلقه شبکه رمزگذار را ایجاد میکند. در بخش دوم برای ایجاد شبکه رمزگشا باید حلقه دیگری بر روی لیست self.nConcolutionT ایجاد کنیم:
def Create(self,
trX:np.ndarray):
_, self.h, self.w, self.c = trX.shape
self.InputShape = (self.h, self.w, self.c)
self.Model = mod.Sequential(name='Autoencoder')
self.Model.add(lay.InputLayer(input_shape=self.InputShape))
for i in self.nConvolution:
self.Model.add(lay.Conv2D(filters=i,
kernel_size=(3, 3),
padding='same'))
self.Model.add(lay.LeakyReLU(alpha=0.2))
self.Model.add(lay.MaxPooling2D(pool_size=(2, 2),
padding='same'))
for i in self.nConvolutionT:
به ازای هر عدد i موجود در لیست، یک لایه Convolution Transpose و سپس یک لایه Leaky ReLU اضافه میکنیم:
def Create(self,
trX:np.ndarray):
_, self.h, self.w, self.c = trX.shape
self.InputShape = (self.h, self.w, self.c)
self.Model = mod.Sequential(name='Autoencoder')
self.Model.add(lay.InputLayer(input_shape=self.InputShape))
for i in self.nConvolution:
self.Model.add(lay.Conv2D(filters=i,
kernel_size=(3, 3),
padding='same'))
self.Model.add(lay.LeakyReLU(alpha=0.2))
self.Model.add(lay.MaxPooling2D(pool_size=(2, 2),
padding='same'))
for i in self.nConvolutionT:
self.Model.add(lay.Conv2DTranspose(filters=i,
kernel_size=(3, 3),
strides=(2, 2),
padding='same'))
self.Model.add(lay.LeakyReLU(alpha=0.2))
برای لایههای عکس پیچش نیز ابعاد 3×3 برای فیلترها در نظر میگیریم. اما با این تنظیمات، تصویر خروجی شبکه در ابعاد 7×7 خواهد بود که مناسب نیست. بنابراین با تعیین stride=(2,2) برای این لایه، این مشکل رفع میشود. توجه داشته باشید که Stride انجام گامهای حرکتی برای فیلتر را تعیین میکند که در لایه Convolution با افزایش آن ابعاد تصویر خروجی کاهش مییابد اما در لایه Convolution Transpose عکس آن رخ میدهد.
در انتهای این بخش، تصاویری با ابعاد 28×28 خواهیم داشت، اما به تعداد آخرین لایه عکس پیچش. برای مثال اگر آخرین لایه عکس پیچش دارای 32 فیلتر باشد، ابعاد تنسور (Tensor) خروجی 28×28×32 خواهد بود. برای رفع این مشکل، یک لایه پیچش اعمال میکنیم:
def Create(self,
trX:np.ndarray):
_, self.h, self.w, self.c = trX.shape
self.InputShape = (self.h, self.w, self.c)
self.Model = mod.Sequential(name='Autoencoder')
self.Model.add(lay.InputLayer(input_shape=self.InputShape))
for i in self.nConvolution:
self.Model.add(lay.Conv2D(filters=i,
kernel_size=(3, 3),
padding='same'))
self.Model.add(lay.LeakyReLU(alpha=0.2))
self.Model.add(lay.MaxPooling2D(pool_size=(2, 2),
padding='same'))
for i in self.nConvolutionT:
self.Model.add(lay.Conv2DTranspose(filters=i,
kernel_size=(3, 3),
strides=(2, 2),
padding='same'))
self.Model.add(lay.LeakyReLU(alpha=0.2))
self.Model.add(lay.Conv2D(filters=self.c,
kernel_size=(3, 3),
padding='same'))
این لایه به تعداد کانالهای تصویر فیلتر دارد. در این مسئله که قصد داریم تصاویری از طیف خاکستری (Gray Scale) استفاده کنیم، تنها یک کانال خواهیم داشت، بنابراین تصویر خروجی 1×28×28 خواهد بود که صحیح است.
در انتهای شبکه یک لایه فعالساز از نوع Sigmoid نیز اضافه میکنیم:
def Create(self,
trX:np.ndarray):
_, self.h, self.w, self.c = trX.shape
self.InputShape = (self.h, self.w, self.c)
self.Model = mod.Sequential(name='Autoencoder')
self.Model.add(lay.InputLayer(input_shape=self.InputShape))
for i in self.nConvolution:
self.Model.add(lay.Conv2D(filters=i,
kernel_size=(3, 3),
padding='same'))
self.Model.add(lay.LeakyReLU(alpha=0.2))
self.Model.add(lay.MaxPooling2D(pool_size=(2, 2),
padding='same'))
for i in self.nConvolutionT:
self.Model.add(lay.Conv2DTranspose(filters=i,
kernel_size=(3, 3),
strides=(2, 2),
padding='same'))
self.Model.add(lay.LeakyReLU(alpha=0.2))
self.Model.add(lay.Conv2D(filters=self.c,
kernel_size=(3, 3),
padding='same'))
self.Model.add(lay.Activation(activation=act.sigmoid))
این لایه باعث خواهد شد مقادیر بسیار کوچک و بسیار بزرگ در بازه (0,1) قرار بگیرند. توجه داشته باشید که تصاویر مجموعه داده نیز در مراحل پیش پردازش بین 0 و 1 مقیاسبندی (Scaling) خواهند شد.
متد کامپایل
مدلهای Keras پس از ایجاد باید کامپایل (Compile) نیز شوند. به این منظور متد دیگری نیز ایجاد میکنیم تا در ورودی الگوریتم بهینهساز و تابع هزینه مورد نظر را دریافت و مدل را کامپایل کند:
def Compile(self,
Optimizer:opt.Optimizer,
Loss:los.Loss):
توجه داشته باشید که الگوریتمهای بهینهساز Keras از کلاس پایه keras.optimizers.Optimizer ارثبری (Inheritance) میکنند و توابع هزینه آن نیز از کلاس keras.losses.Loss ارثبری میکنند. حال ورودیهای دریافتی را در شی ذخیره و سپس مدل را کامپایل میکنیم:
def Compile(self,
Optimizer:opt.Optimizer,
Loss:los.Loss):
self.Optimizer = Optimizer
self.Loss = Loss
self.Model.compile(optimizer=self.Optimizer,
loss=self.Loss)
به این ترتیب متد کامپایل مدل تکمیل میشود.
متد خلاصه مدل
میتوانیم یک متد نیز برای نمایش خلاصهای از مدل ایجاد کنیم:
def Summary(self):
print('_' * 60)
print('Model Summary:')
self.Model.summary()
print('_' * 60)
این متد در خروجی یک متن پرینت (Print) میکند که لایههای مدل، نوع لایهها، تعداد نورون و تعداد پارامتر هر لایه را نشان میدهد.
متد رسم مدل
متد دیگری نیز برای رسم مدل و شیوه جریان اطلاعات در آن ایجاد میکنیم. این متد در خروجی یک تصویر از ساختار مدل ذخیره خواهد کرد:
def Plot(self):
ut.plot_model(self.Model,
to_file='Model.png',
show_shapes=True,
dpi=1536)
توجه داشته باشید که تابع keras.utils.plot_model ورودیهای دیگری نیز دارد که موارد دیگری را در رسم مدل کنترل میکنند. ورودی DPI مخفف Dot Per Inch است و وضوح تصویر ایجاد شده را تعیین میکند.
متد آموزش مدل
شبکه عصبی ایجاد شده، باید بتواند بر روی مجموعه داده آموزش (Train Dataset) آموزش داده شود و همزمان بر روی مجموعه داده اعتبارسنجی (Validation Dataset) اعتبارسنجی شود. به این منظور یک متد با نام Fit ایجاد میکنیم که در ورودی مجموعه داده آموزش، مجموعه داده اعتبارسنجی، تعداد مراحل آموزش و سایز دسته (Batch) را دریافت میکند
def Fit(self,
trX:np.ndarray,
trY:np.ndarray,
vaX:np.ndarray,
vaY:np.ndarray,
nEpoch:int,
sBatch:int):
حال در اولین اقدام، دو ورودی nEpoch و sBatch را در شی ذخیره میکنیم:
def Fit(self,
trX:np.ndarray,
trY:np.ndarray,
vaX:np.ndarray,
vaY:np.ndarray,
nEpoch:int,
sBatch:int):
self.nEpoch = nEpoch
self.sBatch = sBatch
حال میتوانیم متد fit مربوط به مدلهای Keras را فراخوانی کنیم. این متد در خروجی History مربوط به آموزش مدل را برمیگرداند که خطای مدل در طول مراحل را نشان میدهد:
self.History = self.Model.fit(x=trX,
y=trY,
batch_size=sBatch,
epochs=nEpoch,
validation_data=(vaX, vaY),
shuffle=True).history
توجه داشته باشید که از شی خروجی این متد، تنها یک Attribute به نام history نیاز است، به همین دلیل در خط انتهای این Attribute انتخاب شده است.
متد پیش بینی
برای دریافت خروجیهای مدل برای هر ورودی، باید یک متد دیگری نیز با نام Predict ایجاد کنیم که در ورودی آرایه مربوط به تصاویر ورودی را دریافت کند و در خروجی پیشبینی مدل را برگرداند:
def Predict(self,
X:np.ndarray) -> np.ndarray:
P = self.Model.predict(X, verbose=0)
return P
توجه داشته باشید که ورودی verbose الزامی نیست، اما به این دلیل که در صورت خاموش نشدن، با هربار پیشبینی متونی در خروجی پرینت میکند، بهتر است خاموش شود. نمایش این نتایج در برخی شرایط میتواند بسیار مفید باشد.
متد رسم نمودار خطا
برای بررسی بهبود مدل در طول آموزش و عدم بیشبرازش (Overfitting) آن، میتواند خطای مدل برای دو مجموعه داده آموزش و اعتبارسنجی را در یک نمودار کنار هم آورد. به این منظور متد دیگری ایجاد میکنیم:
def LossPlot(self):مراحل آموزش شبکه عصبی از 1 تا self.nEpoch است، بنابراین خواهیم داشت:
def LossPlot(self):
T = np.arange(start=1,
stop=self.nEpoch + 1,
step=1)
حال میتوانیم دو نمودار برای خطای آموزش و اعتبارسنجی در دو رنگ متفاوت اضافه کنیم:
def LossPlot(self):
T = np.arange(start=1,
stop=self.nEpoch + 1,
step=1)
plt.plot(T,
self.History['loss'],
ls='-',
lw=1.2,
c='teal',
label='Train')
plt.plot(T,
self.History['val_loss'],
ls='-',
lw=1.2,
c='crimson',
label='Validation')
برای اینکه نمودار قابل فهم باشد و به خوبی اطلاعات را به مخاطب انتقال دهد، نیاز است که اسم هر منحنی، توضیحات نمودار و اسم هر محور نیز آورده شود، این موارد را اضافه کرده و نمودار را نمایش میدهیم:
def LossPlot(self):
T = np.arange(start=1,
stop=self.nEpoch + 1,
step=1)
plt.plot(T,
self.History['loss'],
ls='-',
lw=1.2,
c='teal',
label='Train')
plt.plot(T,
self.History['val_loss'],
ls='-',
lw=1.2,
c='crimson',
label='Validation')
plt.title('Model Loss Plot Over Training Epochs')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.yscale('log')
plt.legend()
plt.show()
به این ترتیب این متد خواهد توانست نمودار خطای مدل در طول آموزش را رسم و نمایش دهد.
متد نمایش نتایج
به ازای هر تصویر موجود در مجموعه داده، سه تصویر زیر وجود دارد:
- تصویر اولیه
- تصویر حاصل از اضافه کردن نویز به تصویر اولیه
- خروجی شبکه خودرمزگذار پس از دریافت تصویر نویزدار
مقایسه این 3 تصویر در کنار هم، میتواند تا حدود زیادی عملکرد مدل را برای ما نشان دهد. بنابراین متد دیگری نیز ایجاد میکنیم که در انتهای آموزش، مجموعه داده آزمایش را دریافت کند و به ازای تمامی دادهها این سه تصویر را در کنار هم رسم کند:
def PlotResults(self,
X:np.ndarray,
Y:np.ndarray):
در اولین قدم، خروجی مدل را برای ورودیها محاسبه میکنیم:
def PlotResults(self,
X:np.ndarray,
Y:np.ndarray):
P = self.Predict(X)
برای مخلوط کردن دادهها و به هم ریختن ترتیب آنها، ابتدا تعداد آنها را محاسبه کرده، سپس Index آنها را از 0 تا شماره آخرین داده ایجاد میکنیم و در نهایت با استفاده از تابع numpy.random.shuffle آن را بُر میزنیم:
def PlotResults(self,
X:np.ndarray,
Y:np.ndarray):
P = self.Predict(X)
nD = X.shape[0]
I = np.arange(start=0, stop=nD, step=1)
np.random.shuffle(I)
حال یک حلقه بر روی آرایه I ایجاد میکنیم:
def PlotResults(self,
X:np.ndarray,
Y:np.ndarray):
P = self.Predict(X)
nD = X.shape[0]
I = np.arange(start=0, stop=nD, step=1)
np.random.shuffle(I)
for i in I:
تنها رسم تصاویر ممکن است میزان بهبود را به خوبی منتقل نکند، به همین دلیل جذر مربعات خطای نرمالشده را نیز برای هر دو تصویر نویزدار و خروجی شبکه عصبی با توجه به تصویر اولیه محاسبه میکنیم:
def PlotResults(self,
X:np.ndarray,
Y:np.ndarray):
P = self.Predict(X)
nD = X.shape[0]
I = np.arange(start=0, stop=nD, step=1)
np.random.shuffle(I)
for i in I:
e1 = 100 * np.power(Y[i] - X[i], 2).mean() ** 0.5
e2 = 100 * np.power(Y[i] - P[i], 2).mean() ** 0.5
توجه داشته باشید که مقدار e1 تنها تحت تاثیر نویز اضافه شده اولیه است و معیار ما برای سنجش عملکرد مدل است. مقدار e2 قابل بهبود است و در بهترین شرایط برابر با صفر خواهد بود که غیرقابل دستیابی است. بنابراین کم بودن e2 از e1 میتواند کارآمدی شبکه عصبی خودرمزگذار را نشان دهد اما برای نتایج قابل قبول باید e2 به شکل معناداری کمتر از e1 باشد.
حال میتوانیم با matplotlib.pyplot.subplot صفحه را به سه بخش تقسیم کنیم و در هر بخش یک تصویر را رسم کنیم:
def PlotResults(self,
X:np.ndarray,
Y:np.ndarray):
P = self.Predict(X)
nD = X.shape[0]
I = np.arange(start=0, stop=nD, step=1)
np.random.shuffle(I)
for i in I:
e1 = 100 * np.power(Y[i] - X[i], 2).mean() ** 0.5
e2 = 100 * np.power(Y[i] - P[i], 2).mean() ** 0.5
plt.subplot(1, 3, 1)
plt.imshow(Y[i], cmap='gray')
plt.title('Main Image')
plt.xlabel('NRSE: 0 %')
plt.subplot(1, 3, 2)
plt.imshow(X[i], cmap='gray')
plt.xlabel(f'NRSE: {e1:.2f} %')
plt.title('Noised Image')
plt.subplot(1, 3, 3)
plt.imshow(P[i], cmap='gray')
plt.xlabel(f'NRSE: {e2:.2f} %')
plt.title('Denoised Image')
plt.show()
توجه داشته باشید که توضیح هر تصویر در بالای آن با استفاده از matplotlib.pyplot.title نشان داده میشود، بنابراین میتوان خطای هر تصویر را نسبت به تصویر هدف، به کمک matplotlib.pyplot.xlabel نمایش دهیم. به این ترتیب این متد قادر خواهد بود عملکرد شبکه عصبی خودرمزگذار را هم به صورت بصری و هم به صورت عددی نمایش دهد.
به این ترتیب پیادهسازی کلاس AEDN و متدهای آن به پایان میرسد.
تنظیمات برنامه
متغیرهایی در طول اجرای برنامه مورد نیاز خواهند بود که در ابتدای استفاده از کد نوشته شده آنها را تعریف میکنیم:
sVa = 0.2
nConvolution = [64, 32]
RandomState = 0
Optimizer = opt.Adam()
Loss = los.BinaryCrossentropy()
nEpoch = 10
sBatch = 128
این متغیرها به ترتیب موارد زیر را تعیین میکنند:
- متغیر sVa سهم دادههای اعتبارسنجی از دادههای آموزش را نشان میدهد. مقدار 0.2 این متغیر به این معنی است که 20% از دادههای آموزش برای اعتبارسنجی جدا خواهند شد.
- متغیر nConvolution لیستی از اعداد صحیح است که تعداد فیلترها یا کرنلهای (Kernel) لایههای پیچشی را تعیین میکند. تعداد فیلترهای لایههای عکس پیچشی با ترتیب عکس این لیست خواهد بود.
- متغیر RandomState برای ایجاد امکان بازتولید (Reproducible) نتایج است. در صورتی که این متغیر None باشد در هر بار اجرا نتایج با یکدیگر متفاوت خواهند بود و امکان بازتولید نتایج قبلی وجود ندارد؛ اما در صورتی که یک عدد صحیح تعریف شود، نتایج قابل بازتولید خواهد بود.
- متغیر Optimizer الگوریتم بهینهساز مورد استفاده در آموزش شبکه عصبی است. الگوریتمهای مختلفی مثل SGD, RMSprop, Adadelta, …. نیز در کتابخانه Keras وجود دارد که با توجه به ماهیت مسئله میتوانند استفاده شوند. الگوریتم Adam دارای سه پارامتر مهم زیر است که رفتار آن را تعیین میکنند:
- نرخ یادگیری که با ورودی learning_rate تعیین میشود و مقدار پیشفرض 0.001 دارد.
- پارامتر تخمین مومنتوم (Momentum) اولیه که با ورودی beta_1 تعیین میشود و مقدار پیشفرض 0.9 دارد.
- پارامتر تخمین مومنتوم ثانویه که با ورودی beta_2 تعیین میشود و مقدار پیشفرض 0.999 دارد.
- متغیر Loss تابع هزینه مورد استفاده برای آموزش مدل را تعیین میکند. در این مسئله، به این که روشن یا خاموش بودن هر پیکسل بیشتر از مقدار دقیق عددی ان اهمیت دارد، تابع هزینه Binary Crossentropy استفاده شده است. توجه داشته باشید که مقدار پیکسلها بین 0 و 1 مقیاسبندی شدهاند و خروجی شبکه عصبی نیز از یک لایه فعالسازی Sigmoid حاصل میشود که این اعداد نیز همواره بین 0 و 1 خواهد بود. اگر این شرایط بر روی مسئله حاکم نباشد، میتوان سایر توابع هزینه همچون Mean Squared Error, Mean Absolute Error, Huber را استفاده کرد.
- متغیر nEpoch تعداد مراحل آموزش مدل را تعیین خواهد کرد. با توجه به آزمون و خطا و پیچیدگی مسئله، میتوان مقدار این متغیر را تعریف کرد.
- متغیر sBatch سایز دستهها را برای آموزش مدل تعیین میکند. معمولاً از توانهای 2 به عنوان سایز دسته استفاده میشود. مقادیر بین 32 تا 256 برای این متغیر قابل قبول است.
فراخوانی مجموعه داده
پس از تعیین تنظیمات، مجموعه داده MNIST را فراخوانی میکنیم:
(trvaY, _), (teY, _) = dt.mnist.load_data()توجه داشته باشید که برای مسائل عادی طبقهبندی (Classification)، این فراخوانی به شکل زیر انجام میشود:
(trvaX, trvaY), (teX, teY) = dt.mnist.load_data()در این فراخوانی متغیرهای teY و trvaY مربوط به برچسب (Label) تصاویر هستند که در این مسئله نیاز نداریم.
اصلاح ابعاد مجموعه داده
هدف شبکه، پیشبینی تصاویر واقعیت است، بنابراین تصاویر را به عنوان هدف یا Y میشناسیم. ابعاد این دو ماتریس به شکل زیر قابل مشاهده است:
print(f'trvaY: {trvaY.shape}')
print(f'teY: {teY.shape}')
که پس از اجرا خواهیم داشت:
trvaY: (60000, 28, 28)
teY: (10000, 28, 28)
به این ترتیب مشاهده میکنیم که تصاویری 28×28 داریم. به دلیل اینکه تصاویر در مقیاس خاکستری هستند، دارای تنها یک کانال خواهد بود، بنابراین بعد چهارم این ماتریس 1 بوده که حذف شده است. مجموعه داده آموزش و اعتبارسنجی در مجموع شامل 60 هزار تصویر و مجموعه داده آزمایش شامل 10 هزار تصویر است. برای اینکه بعد چهارم را به مجموعه داده اضافه کنیم، از تابع numpy.expand_dims استفاده میکنیم:
trvaY = np.expand_dims(trvaY, axis=-1)
teY = np.expand_dims(teY, axis=-1)
پس از این کد، ابعاد مجموعه داده به شکل زیر خواهد بود:
trvaY: (60000, 28, 28, 1)
teY: (10000, 28, 28, 1)
بنابراین مجموعه داده به ابعاد مورد نیاز میرسد.
اصلاح مقیاس مجموعه داده
مقادیر پیکسلها اعدادی بین 0 تا 255 است. برای بررسی این مقادیر میتوان به شکل زیر عمل کرد:
print(f'Min: {trvaY.min()}')
print(f'Max: {trvaY.max()}')
که نتایج به شکل زیر خواهد بود:
Min: 0
Max: 255
برای اینکه این مقادیر بین 0 و 1 مقیاسبندی شوند، آنها را بر 255 تقسیم میکنیم:
trvaY = trvaY / 255
teY = teY / 255
پس از اعمال کد فوق، بیشترین و کمترین مقادیر به شکل زیر خواهد بود:
Min: 0.0
Max: 1.0
بنابراین مقادیر به بازه مورد نظر منتقل میشود.
اصلاح جنس مقادیر مجموعه داده
مقادیر مجموعه داده از نوع float64 هستند. این موضوع را میتوان به شکل زیر متوجه شد:
print(f'dtype: {trvaY.dtype}')که خواهیم داشت:
dtype: float64این مورد به تنهایی اشکال خاصی به شمار نمیرود، اما به این دلیل که از مجموعه داده تصویری استفاده میکنیم، جنس float64 حجم بیشتری در حافظه RAM یا Random Access Memory اشغال میکند. میتوانیم با تغییر جنس مجموعه داده از float64 به float32 حجم اشغالشده را نصف کنیم و تغییرات خیلی کمی در مقادیر پیکسلها شاهد باشیم. به این منظور کد زیر را اعمال میکنیم:
trvaY = trvaY.astype('float32')
teY = teY.astype('float32')
پس از اجرای کد فوق، دوباره جنس مجموعه داده را بررسی میکنیم، که خواهیم داشت:
dtype: float32برای بررسی تغییرات حجم مجموعه داده در نتیجه این تغییرات، میتوان تکه کد زیر را قبل و بعد از تغییر جنس اجرا کرد:
print(f'trvaY Size: {trvaY.size * trvaY.itemsize}')این کد قبل از تغییر جنس مقدار 376320000 بایت (Byte) را نشان میدهد. پس از تغییر جنس این عدد نصف شده و به مقدار 188160000 بایت تغییر مییابد. توجه داشته باشید که این عملیات، باعث صرفهجویی به اندازه 188.16 مگابایت (Megabyte) میشود.
توجه داشته باشید که Attribute با نام size برای آرایههای Numpy، تعداد اعضا و درایههای آن آرایه را نشان میدهد. Attribute بعدی که با نام itemsize است، اندازه فضای اشغال شده توسط هر درایه از آرایه را نشان میدهد. بدیهی است که حاصلضرب این دو عدد، مجموع فضای اشغالشده توسط کل آرایه را نشان خواهد داد.
تولید تصاویر نویزدار
تصاویر هدف شبکه عصبی آماده استفاده است. حال باید تصاویر ورودی شبکه عصبی را بسازیم. این تصاویر از نسخه اصلی تصاویر خواهند بود با این تفاوت که یک آرایه نویز تصادفی به آن اضافه خواهد شد. به منظور نویز، از یک توزیع نرمال (Normal Distribution) با میانگین صفر و انحراف معیار 0.3 استفاده خواهیم کرد. به این منظور تابع numpy.random.normal مناسب است:
trvaX = trvaY + np.random.normal(loc=0, scale=0.3, size=trvaY.shape)
teX = teY + np.random.normal(loc=0, scale=0.3, size=teY.shape)
بعد از اعمال کد فوق، برخی مقادیر آرایه، اعدادی خارج از بازه [0,1] به خود خواهند گرفت. به منظور جلوگیری از این اتفاق، از تابع numpy.clip استفاده میکنیم:
trvaX = np.clip(a=trvaX, a_min=0, a_max=1)
teX = np.clip(a=teX, a_min=0, a_max=1)
حال مجموعه داده آماده است.
تقسیم مجموعه داده
مجموعه داده MNIST موجود در Keras خود در ابتدا به مجموعه داده آموزش و آزمایش تقسیم شده است. با توجه به اینکه قصد داریم مجموعه داده اعتبارسنجی نیز داشته باشیم، از تابع sklearn.model_selection.train_test_split استفاده میکنیم:
trX, vaX, trY, vaY = ms.train_test_split(trvaX,
trvaY,
test_size=sVa,
random_state=0,
shuffle=True)
توجه داشته باشید که به جای این فرآیند، میتوانید در هنگام fit کردن شبکه عصبی، به جای ورودی validation_data ورودی دیگری به نام validation_split را مقداردهی کنیم. در این شرایط مجموعه داده داخل خود Keras تقسیم میشود. برخی مواقع، تقسیم دستی مجموعه داده اعتبارسنجی نیاز است اما در مواردی مشابه این حالت میتوان آن را به متد fit کتابخانه Keras سپرد.
مصورسازی مجموعه داده
پس از آمادهسازی مجموعه داده، میتوانیم چند مورد از آن را نمایش دهیم. با توجه به اینکه این فرآیند باید تصادفی باشد، به شکل زیر عمل میکنیم:
nDtr = trX.shape[0]
I = np.arange(start=0, stop=nDtr, step=1)
np.random.shuffle(I)
for i in I[:2]:
plt.subplot(1, 2, 1)
plt.imshow(trY[i], cmap='gray')
plt.title('Main Image')
plt.subplot(1, 2, 2)
plt.imshow(trX[i], cmap='gray')
plt.title('Noised Image')
plt.show()
در سطر پنجم این کد، عبارت [:2] استفاده شده که باعث میشود تنها دو مورد نمایش داده شود. میتوان این عدد را برحسب نیاز افزایش داد. پس از اجرای کد فوق، دو نمودار زیر حاصل میشود:
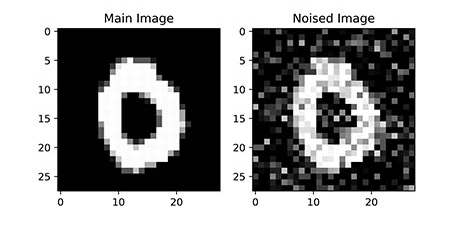
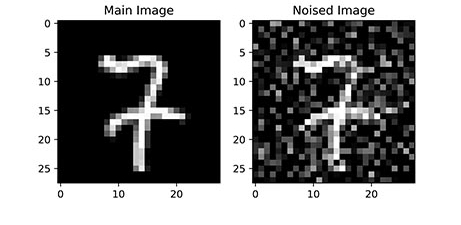
به این ترتیب مشاهده میکنیم که تصاویر واضح اولیه، به خوبی نویزدار شدهاند اما همچنان عدد نوشته شده قابل تشخیص است. از شبکه عصبی انتظار داریم عدد اصلی نوشته شده را نگه داشته و سایر نقاط با مقدار تصادفی و نامناسب را حذف کند.
ایجاد و آموزش شبکه عصبی خودرمزگذار
در ادامه سعی میکنیم حذف نویز از تصاویر با شبکه های عصبی خودرمزگذار را بررسی کنیم. حال میتوانید با استفاده از کلاس نوشته شده، شبکه را ایجاد کنیم:
DN = AEDN(nConvolution, RandomState=RandomState)به این طریق شی ایجاد میشود. حال با وارد کردن X مجموعه داده آموزش، شبکه عصبی را ایجاد میکنیم:
DN.Create(trX)خلاصه مدل
پس از ایجاد مدل، میتوانیم Summary آن را نمایش دهیم:
DN.Summary()در خروجی کد فوق خواهیم داشت:
Model Summary:
Model: "Autoencoder"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
conv2d (Conv2D) (None, 28, 28, 64) 640
leaky_re_lu (LeakyReLU) (None, 28, 28, 64) 0
max_pooling2d (MaxPooling2D (None, 14, 14, 64) 0
)
conv2d_1 (Conv2D) (None, 14, 14, 32) 18464
leaky_re_lu_1 (LeakyReLU) (None, 14, 14, 32) 0
max_pooling2d_1 (MaxPooling (None, 7, 7, 32) 0
2D)
conv2d_transpose (Conv2DTra (None, 14, 14, 32) 9248
nspose)
leaky_re_lu_2 (LeakyReLU) (None, 14, 14, 32) 0
conv2d_transpose_1 (Conv2DT (None, 28, 28, 64) 18496
ranspose)
leaky_re_lu_3 (LeakyReLU) (None, 28, 28, 64) 0
conv2d_2 (Conv2D) (None, 28, 28, 1) 577
activation (Activation) (None, 28, 28, 1) 0
=================================================================
Total params: 47,425
Trainable params: 47,425
Non-trainable params: 0
_________________________________________________________________
به این ترتیب مشاهده میکنیم که مدل دارای یک لایه خروجی و 11 لایه مخفی است. ابعاد خروجی هر لایه در مقابل آن نوشته شده است. تعداد پارامترهای استفاده شده در هر لایه نیز در انتهای هر سطر آورده شده است. توجه داشته باشید که تنها لایههای پیچشی و عکس پیچشی دارای پارامتر و توانایی یادگیری است. نکته مهم دیگر، ابعاد 7×7×32 در انتهای شبکه رمزگذار است. در خروجی این شبکه، 32 تصویر با ابعاد 7×7 برگردانده میشود که اطلاعات پراهمیت تصویر ورودی را در خود نگهداشتهاند. هر لایه Maxpolling2D باعث نصف شدن ابعاد تصویر ورودی شدهاند، در مقابل هر لایه Conv2DTranspose باعث دو برابر شدن ابعاد تصویر شدهاند.
خروجی آخرین لایه عکس پیچشی، ابعاد 28×28×64 دارد که مناسب نیست. لایه پیچشی بعدی که تنها یک فیلتر دارد، این ابعاد را اصلاح و به مقدار صحیح میرساند. این شبکه در مجموعه 47425 پارامتر دارد که همگی قابل آموزش هستند.
نمودار مدل
میتوانیم متد Plot را نیز استفاده کنیم تا ساختار مدل را به شکل بصری در قالب تصویر ببینیم. توجه داشته باشید که تابع keras.utils.plot_model از کتابخانههای pydot و graphviz و برنامه graphviz استفاده میکند. در صورت نصب نبودن این موارد، این سطر از کد دچار مشکل خواهد شد که میتوان به سادگی آن را کامنت (Comment) کرد:
DN.Plot()در خروجی این کد یک تصویر با نام Model.png در کنار برنامه ایجاد خواهد شد:
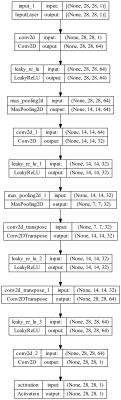
به این ترتیب مشاهده میکنیم که اطلاعات مربوط به ساختار موجود در Summary در این تصویر نیز ایجاد شده است. این تابع برای نمایش جریان اطلاعات (Information Flow) در شبکههای عصبی non-Sequential بسیار مفید است.
کامپایل کردن مدل برای حذف نویز از تصاویر با شبکه های عصبی خودرمزگذار
مدل ایجاد شده است. برای آموزش آن باید مدل را کامپایل کنیم. به این منظور متد نوشته شده را فراخوانی میکنیم:
DN.Compile(Optimizer, Loss)آموزش مدل
پس از کامپایل کردن مدل، میتوانیم آن را بر روی مجموعه داده آموزش دهیم. به این منظور ورودیهای مورد نظر را وارد کرده و متد Fit را فراخوانی میکنیم:
DN.Fit(trX, trY, vaX, vaY, nEpoch, sBatch)اجرای این بخش از کد اندکی زمانبر خواهد بود. پس از اتمام، مدل آموزشدیده خواهد بود و میتوان در اولین قدم نمودار خطا را رسم کرد:
DN.LossPlot()پس از اجرای این کد، نمودار زیر حاصل خواهد شد:
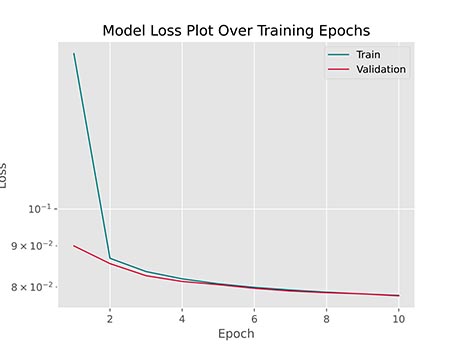
به این ترتیب مشاهده میکنیم که خطای مجموعه داده آموزش همزمان با مجموعه داده اعتبارسنجی درحال کاهش است که نشاندهنده بدون مشکل بودن فرآیند آموزش مدل است. نمودار آورده شده نیمهلگاریتمی است و به این دلیل بخش انتهای از آموزش به خوبی بهبود را نشان میدهد. در صورت عدم استفاده از این حالت، بخش انتهایی نمودار یک شکل ثابت و صاف به خود خواهد گرفت.
رسم نمودار نتایج پس از حذف نویز از تصاویر با شبکه های عصبی خودرمزگذار
پس از نمودار خطا، میتوانیم متد PlotResults را برای مجموعه داده آزمایش فراخوانی کنیم:
DN.PlotResults(teX, teY)در خروجی کد فوق، برای هر 10 هزار داده موجود در مجموعه داده آزمایش، یک نمودار قابل رسم است که دو مورد از آنها در زیر آورده شده است:
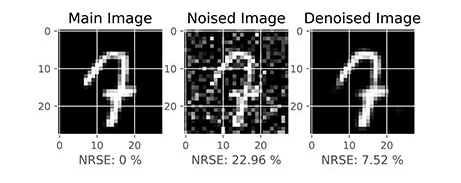
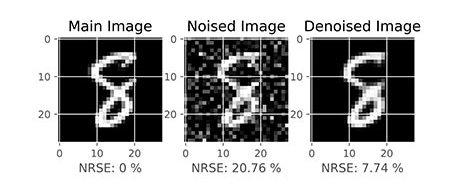
به این ترتیب مشاهده میکنیم که تصاویر نویزدار به صورت میانگین 20% خطا دارند. در مقابل تصویر بازسازی شده (Reconstructed) به صورت میانگین دارای 7% خطا است. بنابراین میتوان گفت مدل توانسته تا حدود زیادی نویز را حذف کند و در مقابل پیکسلهای نامربوط به نویز را روشن نگهدارد. به صورت بصری نیز میتوان دید که مدل عملکرد خوبی از خود نشان داده است.
جمع بندی حذف نویز از تصاویر با شبکه های عصبی خودرمزگذار
به این ترتیب پیادهسازی شبکه عصبی خودرمزگذار برای حذف نویز از تصاویر با شبکه های عصبی خودرمزگذار به اتمام میرسد. به منظور مطالعه بیشتر میتوان موارد زیر را بررسی کرد:
- اگر تابع هزینه Mean Squared Error استفاده شود، چه مشکل پیش خواهد آمد؟
- لایه عکس پیچش چگونه کار میکند؟ چرا به آن Convolution Transpose گفته میشود؟
- لایههای Maxpooling2D را حذف کرده و در مقابل Stride لایههای پیچشی را تنظیم کنید. در این شرایط دقت مدل چه تغییر مییابد؟
- در برخی معماریها، برای هر بلوک (Block) لایه Batch Normalization نیز در نظر گرفته میشود. اضافه کردن این لایه به مدل نوشته شده، چه تغییری در نتایج ایجاد خواهد کرد؟
- آموزش مدل ایجاد شده، زمانبر است و به لحاظ محاسباتی پرهزینه است. دو متد برای کلاس AEDN تعریف کنید که بتواند مدل آموزش دیده را ذخیره و سپس فراخوانی کند.
- تصویر نویزدار نسبت به تصویر اولیه، دارای خطا است. ارتباط مقدار این خطا با انحراف معیار توزیع نرمال نویزها چیست؟
- آخرین لایه مدل، مربوط به یک لایه فعالسازی از نوع Sigmoid است. نتایج مدل را در صورت حذف این لایه بررسی کنید.
- سایز فیلترهای پیچشی و عکس پیچشی برابر با 3×3 در نظر گرفته شده است. دو حالت 2×2 و 4×4 را نیز بررسی کنید و بهترین مورد را انتخاب کنید.
- مدل را به تعداد مراحل بیشتر آموزش دهید و بررسی کنید که آیا بیشبرازش رخ میدهد یا نه؟

