بررسی معیارهای ارزیابی رگرسیون در پایتون — پیاده سازی + کدها

در مسائل رگرسیون، به دنبال پیشبینی یک یا چند ویژگی هدف براساس ویژگیهای ورودی به مدل هستیم. ویژگی هدف برخلاف مسائل طبقهبندی، پیوسته است. در این آموزش، با معیارهای ارزیابی رگرسیون آشنا میشویم و روش پیادهسازی آنها در پایتون را بیان میکنیم.

معیارهای ارزیابی از سه جهت کاربرد داشته و حائز اهمیت است:
- برای آموزش مدلها میتوانند به عنوان تابع هزینه استفاده شوند.
- برای مقایسه مدلها با یکدیگر میتوانند استفاده شوند.
- برای پیشبینی خطای مدل در مواجه با دادههای جدید استفاده شوند.
به این ترتیب، اهمیت معیارهای ارزیابی رگرسیون در پایتون آشکار میشود. در این مطلب 6 معیار مهم ارزیابی رگرسیون در پایتون به همراه کدهای پایتون را بررسی خواهیم کرد.
وارد محیط برنامهنویسی میشویم و کتابخانههای مورد نیاز را فراخوانی میکنیم:
import numpy as np
import sklearn.metrics as metاز کتابخانه Numpy برای پیادهسازی معیارها و از کتابخانه Scikit-Learn برای استفاده از توابع آماده استفاده خواهیم کرد.
برای یادگیری برنامهنویسی با زبان پایتون، پیشنهاد میکنیم به مجموعه آموزشهای مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
میانگین مربعات خطا یا MSE
«میانگین مربعات خطا» (Mean Squared Error | MSE) یکی از پرکاربردترین معیارها است که هم در آموزش مدلها و هم در مقایسه مدلها استفاده میشود. این معیار دارای بُعد است، به همین دلیل به عنوان گزارش نهایی در مسائل رگرسیون مناسب نیست.
برای محاسبه میانگین مربعات خطا، به شکل زیر عمل میکنیم:
$$ large
operatorname{MSE}(Y, hat{Y})=frac{1}{n} sum_{i=1}^{n}left(Y_{i}-hat{Y}_{i}right)^{2}=frac{1}{n} sum_{i=1}^{n} e_{i}{ }^{2}
$$
رفتار این معیار نسبت به خطای هر داده بهصورت سهمی است.
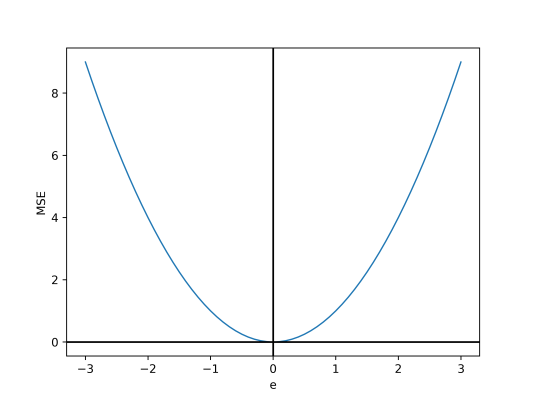
نکته مهم دیگری که در مورد این معیار وجود دارد، وزندهی بیشتر به خطاهای بزرگتر است، به طوری که اگر دو داده با خطاهای 1 و 3 وجود داشته باشد، اثرگذاری داده دوم بیشتر خواهد بود. با توجه به این موضوع، خطا در حالتی که $$e=[2,2]$$ باشد، کمتر از حالتی است که $$e=[1,3]$$ باشد.
این معیار مشتقپذیر بوده و با فرض یک مدل خطی، به شکل زیر میتوان از آن مشتق گرفت:
$$ large
begin{aligned}
&hat{Y}_{i}=a X_{i}+b \
&M S E(Y, hat{Y})=frac{1}{n} sum_{i=1}^{n}left(Y_{i}-a X_{i}-bright)^{2} \
&Rightarrow frac{partial M S E}{partial a}=frac{1}{n} sum_{i=1}^{n} 2left(-X_{i}right)left(Y_{i}-a X_{i}-bright)=-frac{2}{n} sum_{i=1}^{n} X_{i}left(Y_{i}-a X_{i}-bright) \
&Rightarrow frac{partial M S E}{partial b}=frac{1}{n} sum_{i=1}^{n} 2(-1)left(Y_{i}-a X_{i}-bright)=-frac{2}{n} sum_{i=1}^{n}left(Y_{i}-a X_{i}-bright)
end{aligned}
$$
علاوه بر اینکه میتوان از این روابط در آموزش مدلها استفاده کرد، برابر قرار دادن این دو عبارت با صفر و حل کردن دستگاه معادلات حاصل نیز فرمولهای رگرسیون خطی را اثبات میکند.
برای پیادهسازی میانگین مربعات خطا میتوان به شکل زیر عمل کرد:
def MSE(Y:np.ndarray, Yh:np.ndarray):
e = np.subtract(Y, Yh)
se = np.power(e, 2)
mse = np.mean(se)
return mseاز توابع آماده نیز میتوان به شکل زیر استفاده کرد:
mse = met.mean_squared_error(Y, Yh)جذر میانگین مربعات خطا RMSE
«معیار جذر میانگین مربعات خطا» (Root Mean Squared Error | RMSE) با استفاده از رابطه زیر از میانگین مربعات خطا محاسبه میشود:
$$ large
R M S E(Y, hat{Y})=sqrt{M S E(Y, hat{Y})}
$$
دلیل استفاده از جذر میانگین مربعات خطا، یکسان بودن بُعد و مقیاس آن با ویژگی هدف است. برای مثال، اگر یک مدل برای پیشبینی وزن افراد برحسب Kg ایجاد کرده باشیم، واحد میانگین مربعات خطا kg2 خواهد بود، درحالی که که واحد جذر مربعات خطا Kg است. این معیار اغلب در گزارش نتایج استفاده میشود و به عنوان تابع هزینه استفاده نمیشود.
برای پیادهسازی جذر میانگین مربعات خطا میتوان نوشت:
def RMSE(Y:np.ndarray, Yh:np.ndarray):
e = np.subtract(Y, Yh)
se = np.power(e, 2)
mse = np.mean(se)
rmse = mse**0.5
return rmseیا با استفاده از توابع آماده این کار انجام میگیرد:
rmse = met.mean_squared_error(Y, Yh)**0.5جذر مربعات خطای نرمالشده NRMSE
«جذر مربعات خطای نرمالشده» (Normalized Root Mean Squared Error | NRMSE) با استفاده از رابطه زیر محاسبه میشود:
$$ large
operatorname{NRMSE}(Y, hat{Y})=frac{operatorname{RMSE}(Y, hat{Y})}{operatorname{Max}(Y)-operatorname{Min}(Y)}
$$
این معیار، حاصل تقسیم جذر میانگین مربعات خطا بر بازه ویژگی هدف است، به همین دلیل عددی بدون بُعد و واحد بوده و برای گزارش بسیار مناسب است.
میتوان این معیار را به صورت درصدی نیز بیان کرد. برای پیادهسازی خواهیم داشت:
def NRMSE(Y:np.ndarray, Yh:np.ndarray):
e = np.subtract(Y, Yh)
se = np.power(e, 2)
mse = np.mean(se)
rmse = mse**0.5
nrmse = rmse / (np.max(Y) - np.min(Y))
return nrmseیا با استفاده از توابع آماده این کار انجام میگیرد:
nrmse = met.mean_squared_error(Y, Yh)**0.5 / (np.max(Y) - np.min(Y))میانگین قدرمطلق خطا MAE
«میانگین قدرمطلق خطا» (Mean Absolute Error | MAE) به جای به توان 2 رساندن خطاها، از تابع قدرمطلق استفاده میکند و به صورت زیر محاسبه میشود:
$$ large
operatorname{MAE}(Y, hat{Y})=frac{1}{n} sum_{i=1}^{n}left|Y_{i}-hat{Y}_{i}right|=frac{1}{n} sum_{i=1}^{n}left|e_{i}right|
$$
با توجه به اینکه مقادیر به توان نرسیدهاند، واحد میانگین قدرمطلق خطا با ویژگی هدف یکسان خواهد بود.
این معیار با توجه به اینکه از تابع قدرمطلق استفاده میکند، در شرایطی مشتقپذیر نبوده و میتواند در بهینهسازیهای وابسته به گرادیان مشکلساز باشد.
مشکل دیگر این معیار، ضعیف نشدن گرادیان با نزدیک شدن به $$e=0$$ است که باعث مشکلاتی در بهینهسازی و بعضا واگرایی میشود.
در صورتی که در مجموعه داده مقادیر پرت وجود داشته باشد که از صحت آنها اطمینان داریم میانگین مربعات خطا مناسب است، اما در شرایطی که بخواهیم مدل ما نسبت به دادههای پرت پایدارتر باشد، میانگین قدرمطلق خطا گزینه مناسبی است. رفتار این معیار نسبت به خطای هر داده، به صورت قدرمطلقی است:
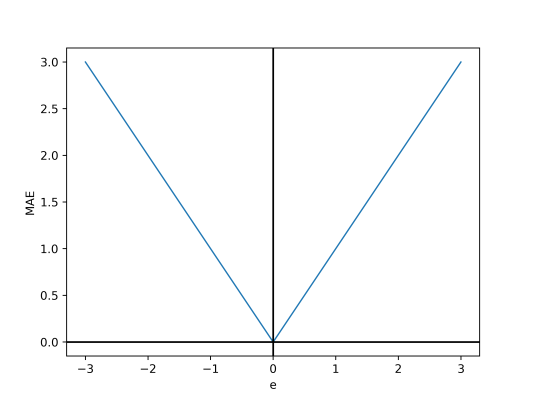
به این ترتیب مشتقناپذیری در $$e=0$$ و شیب ثابت کاملاً مشهود است. از این معیار میتوان برای مقایسه مدلها و همچین گزارش نتایج استفاده کرد. برای پیادهسازی میانگین قدرمطلق خطا مینویسیم:
def MAE(Y:np.ndarray, Yh:np.ndarray):
e = np.subtract(Y, Yh)
ae = np.abs(e)
mae = np.mean(ae)
return maeیا با استفاده از توابع آماده این کار انجام میگیرد:
mae = met.mean_absolute_error(Y, Yh)میانگین درصد قدرمطلق خطا MAPE
«میانگین درصد قدرمطلق خطا» (Mean Absolute Percentage Error | MAPE) مشابه میانگین قدرمطلق خطا است، اما به جای خطا، از خطای نسبی استفاده شده است:
$$ large
operatorname{MAPE}(Y, widehat{Y})=frac{100}{n} sum_{i=1}^{n}left|frac{Y_{i}-hat{Y}_{i}}{Y_{i}}right|=frac{100}{n} sum_{i=1}^{n}left|frac{e_{i}}{Y_{i}}right|
$$
به این ترتیب، معیاری بدون واحد به دست خواهد آمد که برای گزارش نتایج مناسب است.
این معیار نیز مشکلات میانگین مربعات خطا را دارد. مشکل دیگری که در رابطه با میانگین درصد قدرمطلق خطا وجود دارد، احتمال وجود مقادیر بسیار نزدیک به 0 در داده است. در این شرایط، کسر عبارت بسیار کوچک شده و تاثیر شدیدی بر معیار خواهد گزاشت. برای مثال، اگر برای 4 داده داشته باشیم:
| $$left|frac{e}{y}right|$$ | $$e$$ | $$widehat{y}$$ | $$y$$ |
| $$0.2$$ | $$0.1$$ | $$0.4$$ | $$0.5$$ |
| $$9$$ | $$-0.09$$ | $$0.1$$ | $$0.1$$ |
| $$0$$ | $$0$$ | $$1.5$$ | $$1.5$$ |
| $$0.16$$ | $$-0.2$$ | $$1.4$$ | $$1.2$$ |
به این ترتیب مشاهده میکنیم که برای داده دوم قدرمطلق خطای نسبی عدد بسیار بزرگی نسبت به سایر دادهها است که باعث اثرگذاری شدید آن روی معیار میشود. به همین دلیل، در صورت وجود مقادیر نزدیک به $$0$$ در مجموعه داده، معیار میانگین درصد قدرمطلق خطا ترجیح داده نمیشود.
این معیار با خطای نسبی هر داده رابطه قدرمطلقی دارد.
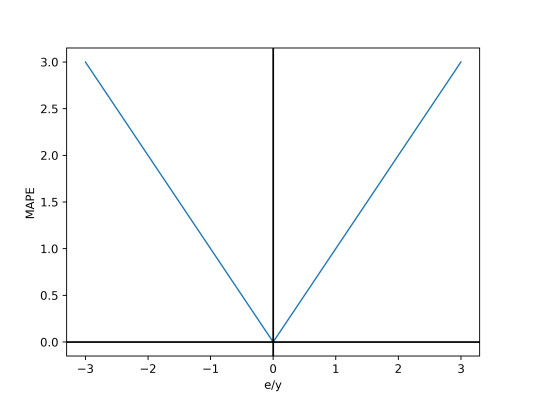
برای پیادهسازی این معیار، مینویسیم:
def MAPE(Y:np.ndarray, Yh:np.ndarray):
e = np.subtract(Y, Yh)
pe = 100 * e / Y
ape = np.abs(pe)
mape = np.mean(ape)
return mapeیا با استفاده از توابع آماده این کار انجام میگیرد:
mape = 100*met.mean_absolute_percentage_error(Y, Yh)تابع آماده استفاده شده در کد بالا عددی از 0 تا 1 در خروجی تولید میکند و برای تبدیل آن به درصد با ضرب در 100 شود.
ضریب تعیین یا امتیاز $$R^2$$
«ضریب تعیین امتیاز» (Coefficient of Determination) برخلاف 5 معیار قبلی، با افزایش، دقت بالای مدل را نشان میدهد. برای محاسبه آن به شکل زیر عمل میکنیم:
$$ large
R^{2}(Y, widehat{Y})=1-frac{sum_{i=1}^{n}left(Y_{i}-widehat{Y}_{i}right)^{2}}{sum_{i=1}^{n}left(Y_{i}-bar{Y}right)^{2}}=1-frac{M S E(Y, widehat{Y})}{sigma^{2}(Y)}
$$
این معیار همواره عددی کوچکتر از 1 است. اگر مدلی همواره میانگین ویژگی هدف را در خروجی تولید کند، مقدار این معیار برابر 0 خواهد بود. ضریب تعیین معمولاً به صورت درصد بیان میشود. از ضریب تعیین تنها برای مقایسه مدلها و گزارش نتایج استفاده میشود. با توجه به اینکه واریانس مجموعه داده عددی ثابت است، با افزایش میانگین مربعات خطا، ضریب تعیین همواره کاهش مییابد.
برای پیادهسازی ضریب تعیین مینویسیم:
def R2(Y:np.ndarray, Yh:np.ndarray):
e = np.subtract(Y, Yh)
se = np.power(e, 2)
mse = np.mean(se)
var = np.var(Y)
r2 = 1 - mse / var
return r2یا با استفاده از توابع آماده خواهیم داشت:
r2 = met.r2_score(Y, Yh)جمعبندی ارزیابی رگرسیون در پایتون
در این آموزش، معیارهای پرکاربرد در مسائل رگرسیون بررسی و پیادهسازی شدند.
برای مطالعه بیشتر میتوان معیارهای جدیدتر مانند AIC، معیارهای اصلاحشده مانند Adjusted R2، معیارهای ترکیبی، معیارهای دارای Threshold و همبستگی بین معیارها را مورد بررسی قرار داد.

