الگوریتم حریصانه چیست؟ – به زبان ساده + مثال کاربردی

در مباحث مربوط به طراحی الگوریتم، موضوع مهمی پیرامون روشهای جستجو مطرح میشود. بهینهترین روشهای جستجو، روشهایی هستند که با کمترین هزینه، بهترین مسیر را پیدا کنند. از میان الگوریتمهای پرکابرد، میتوان به الگوریتم حریصانه اشاره کرد که بر پیدا کردن مسیر با حداقل هزینه تمرکز دارد. در این مطلب، به این سوال پاسخ میدهیم که الگوریتم حریصانه چیست و چه ویژگیها و مزیتها و معایبی دارد. همچنین، برای درک آسان از این الگوریتم، مثالی کاربردی از آن ارائه خواهیم داد.

الگوریتم حریصانه چیست ؟
الگوریتم حریصانه رویکردی برای حل مسائل است که در آن با توجه به وضعیت فعلی، مناسبترین گزینه برای رسیدن به هدف انتخاب میشود و در این نوع الگوریتمها این موضوع اهمیتی ندارد که آیا در پی چنین روشی، بهینهترین نتیجه حاصل میشود یا این معیار در نهایت پرهزینهترین مسیر را به همراه خواهد داشت.
حتی اگر تصمیم اولیه الگوریتم حریصانه نادرست باشد، این الگوریتم برای تصحیح کردن انتخاب خود، به مراحل قبلی باز نخواهد گشت. بدین ترتیب، میتوان گفت این الگوریتم ممکن است به بهینهترین راهحل دست پیدا نکند، زیرا در حین انتخاب مسیر، کل مسیر را مد نظر قرار نمیدهد و صرفاً بر وضعیت جاری تمرکز دارد.
واژه «حریصانه» نیز برای نامگذاری این نوع الگوریتم در برنامه نویسی انتخاب شده است، زیرا در این روش به دنبال پیدا کردن بهترین راهحل و بهترین انتخاب در هر مرحله هستیم، بدون این که گامهای بعدی مسیر یا پیامد حاصل از انتخاب مرحله فعلی را مد نظر قرار دهیم.
الگوریتم حریصانه الگوریتمی ساده و شهودی به حساب میآید که از آن میتوان برای حل مسائل بهینهسازی استفاده کرد. درک این الگوریتم ساده است و افراد برنامه نویس برای پیادهسازی آن با مشکل و پیچیدگی خاصی مواجه نخواهند شد.
همچنین، این الگوریتم برای مسائلی کاربردی است که بتوان آنها را به بخشهای کوچکتر تقسیم کرد و بتوان راهحلهای هر بخش را برای رسیدن به پاسخ کلی مسئله با یکدیگر ترکیب کرد. از این الگوریتم در حل بسیاری از مسائل، نظیر نظریه گراف و برنامه نویسی پویا استفاده میشود.
مثالی از روش حریصانه
از الگوریتم حریصانه معمولاً برای حل مسائلی استفاده میشود که بتوان در آنها دادههای مسئله را در قالب گراف نشان داد. همانطور که در تصویر زیر آمده، گراف از دو جزء یال و گره تشکیل شده است.
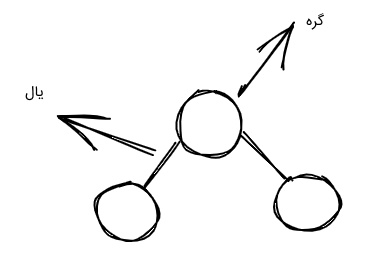
برای درک روال کار این الگوریتم، میتوان از مثالی ساده کمک گرفت. فرض کنید گرافی دارید که هر یک از گرههای آن وزنهای گراف را نشان میدهند. قصد داریم در طول این گراف پیمایش کنیم و مسیری را طی کنیم تا در پی آن بزرگترین مقدار وزن پیدا شود. در تصویر زیر، مثالی از این گراف نشان داده شده است.
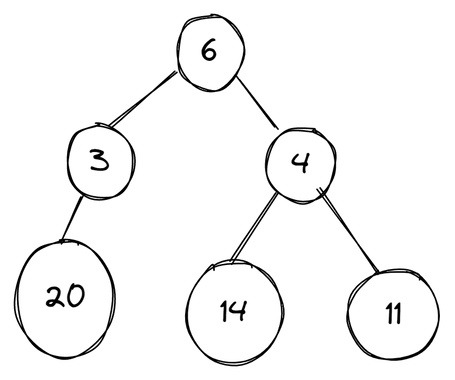
چنانچه بخواهیم با استفاده از روش حریصانه مسیری را در این گراف به نحوی طی کنیم که در نهایت گرههایی با بیشترین وزن انتخاب شوند، از گره ۶ به عنوان گره ریشه آغاز میکنیم. الگوریتم برای ادامه مسیر خود، دو گره ۳ و ۴ را پیش رو دارد. این الگوریتم عدد ۴ را برمیگزیند. سپس، از بین دو گره پیش روی خود، گره ۱۴ را انتخاب میکند و در نهایت کار الگوریتم به اتمام میرسد.
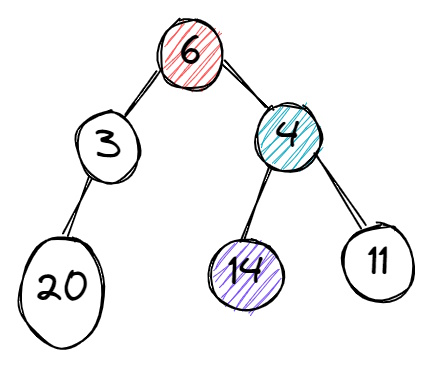
حال اگر بخواهیم همین مسئله را با روشی غیرحریصانه حل کنیم، مسیر طی شده در گراف متفاوت خواهد بود. به عبارتی، چنانچه مسئله فعلی را بخواهیم با روش غیرحریصانه حل کنیم و پیمایش گراف را از گره ۶ شروع کنیم، از بین گرههای پیش رو، عدد ۴ را انتخاب میکنیم و در گام بعد نیز از بین اعداد ۱۱ و ۱۴، عدد ۱۴ را برمیگزینیم.
سپس، همین روال را دوباره از گره ۶ شروع و این بار، عدد ۳ را انتخاب میکنیم. سپس، از بین زیرگرههای عدد ۳، بزرگترین گره را انتخاب میکنیم که در این مثال، فقط یک گره با مقدار ۲۰ وجود دارد.
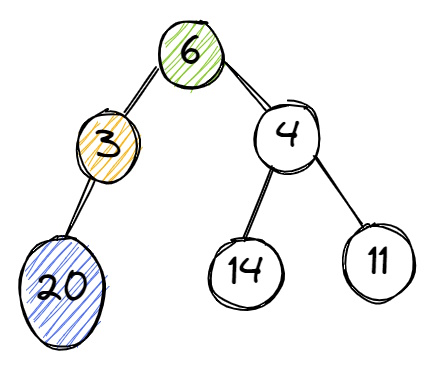
در نهایت، از بین مقادیر انتخاب شده از دو مسیر طی شده در گراف، مسیری را با بزرگترین مقدار انتخاب میکنیم. مسیر اول به مقدار ۱۴ و مسیر دوم به مقدار ۲۰ ختم شد. بدین ترتیب، الگوریتم غیرحریصانه، مسیر دوم را به عنوان نتیجه نهایی انتخاب و مقدار ۲۰ را به عنوان جواب مسئله ارائه میکند.
با مقایسه نتایج دو الگوریتم حریصانه و غیرحریصانه میبینیم که روش حریصانه بهینهترین پاسخ را انتخاب نکرده است. با این حال، از الگوریتم حریصانه در مسائلی استفاده میشود که قصد داریم در زمان کم و با هزینه پایین، تخمین خوبی از پاسخ مسئله داشته باشیم.
مثال دیگری را نیز میتوان برای این الگوریتم ارائه کرد. فرض کنید میخواهیم از موقعیت فعلی خود حرکت کنیم و به مقصد تعیین شده برسیم. برای رسیدن به مقصد، چندین مسیر با مسافتهای متفاوت وجود دارد. در تصویر زیر، مسیرهای متفاوت دو موقعیت مکانی را ملاحظه میکنید.
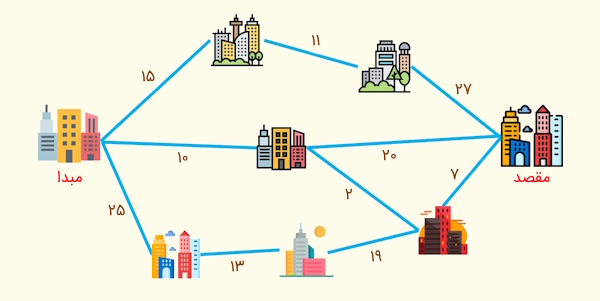
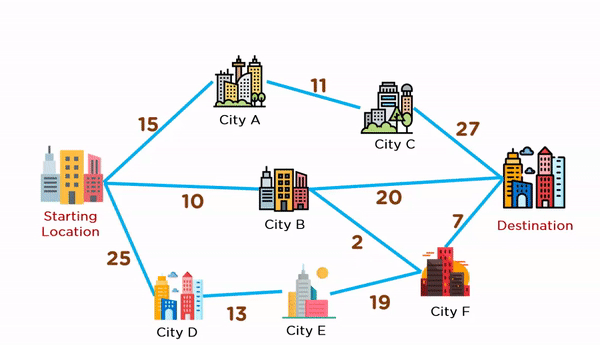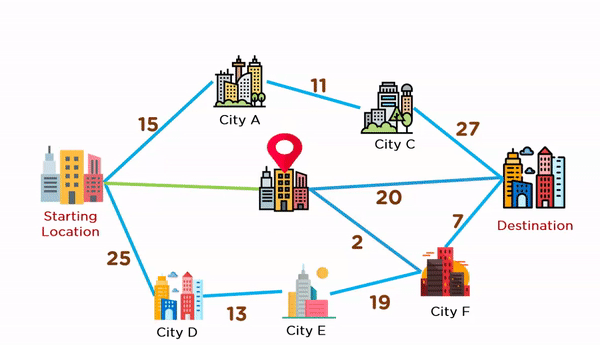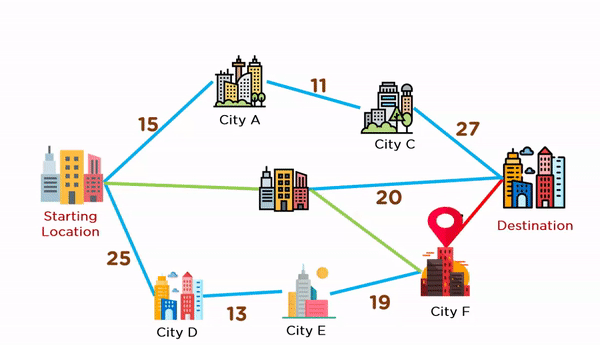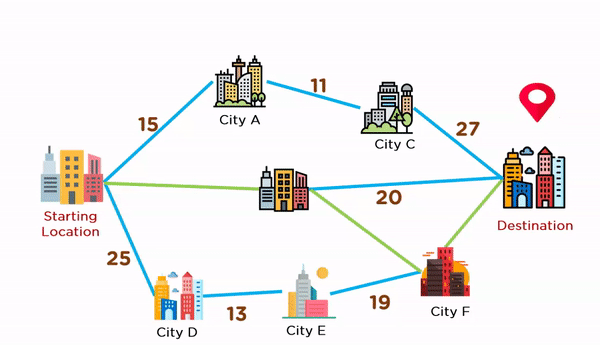
قصد داریم با روش حریصانه مسیری را انتخاب کنیم که کوتاهترین مسافت را داشته باشد. در تصویر زیر، نحوه انتخاب مسیر را با استفاده از روش حریصانه ملاحظه میکنید. در موقعیت مبدا، الگوریتم ۳ مسیر را با مسافتهای ۱۵، ۱۰ و ۲۵ پیش رو دارد که این الگویتم، مسیری با مسافت ۱۰ را انتخاب میکند.
سپس، الگوریتم در مکان B نیز دو مسیر با مسافتهای ۲ و ۲۰ پیش رو دارد که شهر F را با کوتاهترین مسیر انتخاب میکند. در نهایت، تنها یک مسیر با مسافت ۷ تا مقصد باقی میماند که الگوریتم با انتخاب آن، کار خود را به اتمام میرساند.
در بخش بعدی این نوشتار، به ویژگیهای روش حریصانه و مزایا و معایب آن پرداخته شده است.
ویژگی های الگوریتم حریصانه چیست ؟
الگوریتم حریصانه همانند سایر الگوریتمها دارای ویژگیهای منحصربفردی است. یکی از مهمترین ویژگیهای الگوریتم حریصانه این است که سعی دارد راهحل بهینهای را برای مسئله پیدا کند. به عبارتی، این الگوریتم در پی یافتن مقادیر بیشینه و کمینه است و در هر گام از تصمیمگیری، بر گزینههای فعلی خود تمرکز میکند.
در ادامه، سایر ویژگیهای این الگوریتم بیان شدهاند.
- الگوریتم حریصانه، الگوریتمی سریع و کارامد است و از آن برای حل مسائلی با مقیاس بزرگ استفاده میشود.
- پیچیدگی زمانی الگوریتم حریصانه برابر با $$O(n log n)$$ یا $$O(n)$$ است.
- این الگوریتم تنها یک بار اجرا میشود و در حین اجرا، از روش عقبگرد استفاده نمیکند.
- پیادهسازی این الگوریتم بسیار ساده است.
چه زمانی از الگوریتم حریصانه استفاده می شود ؟
پیش از آن که الگوریتمی را برای حل مسئله خود انتخاب کنیم، باید به ۲ پرسش اصلی پاسخ دهیم. اولین پرسش این است که آیا برای حل مسئله به دنبال یافتن بهترین تخمین پاسخ با هزینه زمانی پایین هستیم؟ دومین پرسش در این باره است که آیا برای حل مسئله به دنبال یافتن راهحل بهینه هستیم؟ چنانچه پاسخ هر دو سوال مطرح شده، مثبت باشد، آنگاه الگوریتم حریصانه میتواند یکی از بهترین راهحلها برای حل مسئله ما باشد.
مزایای روش حریصانه
الگوریتم حریصانه دارای مزیتهای مهمی است که در ادامه به آنها اشاره شده است:
- پیادهسازی الگوریتم حریصانه ساده است.
- الگوریتم حریصانه دارای پیچیدگی زمانی پایین است.
- از این الگوریتم میتوان در مسائل پیچیده برای پیدا کردن مقدار تخمینی پاسخ بهراحتی استفاده کرد.
- این الگوریتم به عنوان الگوریتمی کارآمد محسوب میشود، زیرا این الگوریتم تمامی راهحلهای مسئله را بررسی نمیکند.
- درک این الگوریتم ساده است.
معایب الگوریتم حریصانه چیست ؟
الگوریتم حریصانه علیرغم مزیتهایی که دارد، دارای معایبی نیز هست که در ادامه به آنها اشاره میکنیم:
- با توجه به این که الگوریتم حریصانه در هر مرحله بهترین پاسخ را بدون توجه به ادامه مسیر انتخاب میکند، ممکن است در تمامی مسائل، پاسخ بهینه را پیدا نکند.
- از این الگوریتم بهتر است در مسائلی استفاده شود که در آنها به دنبال پیدا کردن مقدار دقیقی به عنوان پاسخ مسئله نیستیم و تنها تخمین مقدار پاسخ نهایی مسئله نیز برای ما کافی است.
- این الگوریتم مناسب مسائلی نیست که شرایط کلی مسئله در آنها تغییر میکند.
کاربردهای روش حریصانه
از الگوریتم حریصانه میتوان برای طراحی و پیادهسازی سایر الگوریتمها نیز استفاده کرد. در این مطلب، به دو الگوریتم Prim و Kruskal میپردازیم که بر پایه روش الگوریتم حریصانه طراحی شدهاند.
الگوریتم Prim بر پایه الگوریتم حریصانه
از روش حریصانه به منظور ساخت درخت پوشای کمینه در الگوریتم پریم استفاده میشود. در این الگوریتم، درخت پوشا مرحله به مرحله ساخته میشود و به منظور ساخت یالهای درخت، از روش حریصانه به نحوی استفاده میشود که مجموع وزنهای یالها کمینه شود.
الگوریتم Prim به عنوان ورودی، گرافی را دریافت میکند و هدف آن ساخت درخت پوشای کمینه است. پیچیدگی زمانی این الگوریتم برابر با $$O(n2)$$ است. در تصویر زیر، مثالی از یک گراف ملاحظه میکنید که قصد داریم با استفاده از الگوریتم Prim بر مبنای روش حریصانه بر روی این گراف پیمایش انجام دهیم، به نحوی که مسیری با کمترین هزینه حاصل شود.
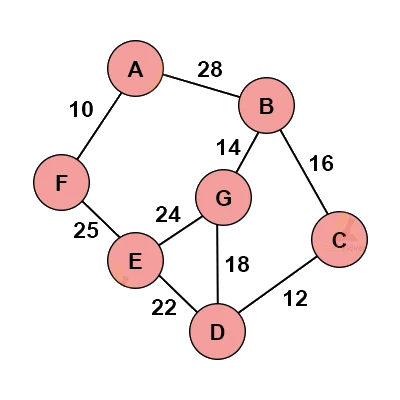
در وهله نخست، الگوریتم Prim گرهای را (نظیر گره A) بهطور تصادفی انتخاب میکند. سپس، از بین یالهای متصل به این گره، یالی انتخاب میشود که کمترین وزن را داشته باشد و گره بعدی متصل به یال انتخاب شده، به عنوان گره جاری در نظر گرفته میشود و همین روال انتخاب یال برای آن گره نیز تکرار میشود.
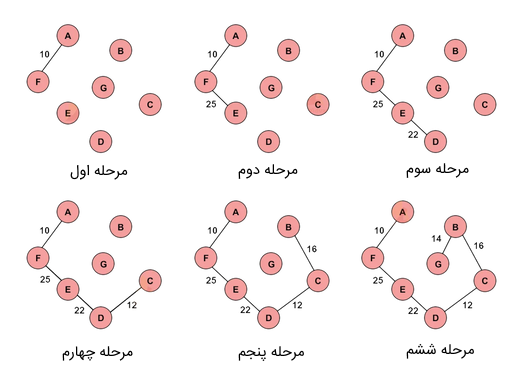
در نهایت، درختی که با استفاده از الگوریتم Prim و انتخاب حریصانه حاصل میشود، در تصویر زیر نشان داده شده است:
استفاده از روش حریصانه در الگوریتم Kruskal
یکی دیگر از الگوریتمهایی که برای یافتن درخت پوشا از یک گراف استفاده میشود، الگوریتم Kruskal است که بر مبنای روش حریصانه کار میکند. درخت حاصل از الگوریتم Kruskal دارای هیچ حلقهای نیست.
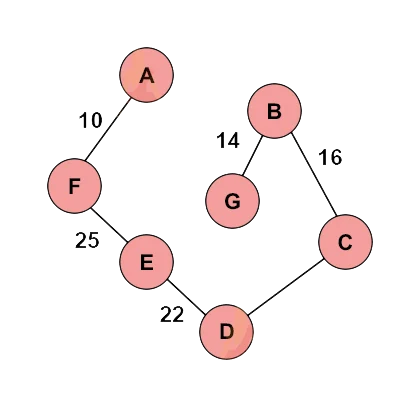
در تصویر زیر، گرافی را ملاحظه میکنید که از آن برای توضیح روال الگوریتم Kruskal استفاده شده است.

قصد داریم با استفاده از الگوریتم Kruskal و بر مبنای روش حریصانه، مسیری را بر روی این گراف پیمایش کنیم که حداقل هزینه را در بر داشته باشد. بدین منظور، در وهله اول نیاز است که بهترتیب، یالهایی با کمترین مقدار هزینه انتخاب شوند، به نحوی که حلقهای شکل نگیرد. در تصویر زیر، روال الگوریتم Kruskal را ملاحظه میکنید.
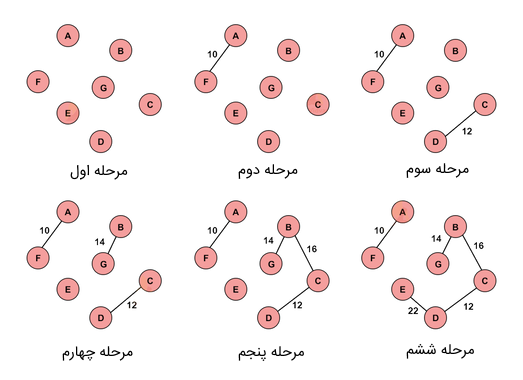
جمعبندی
طراحی الگوریتم و روشهای آن از موضوعات مهم حوزه علوم کامپیوتر محسوب میشود. با کمک این روشها به دنبال پیدا کردن راهی برای حل مسئله هستیم. هر یک از الگوریتمها ویژگیهای منحصربفردی دارند که بنا به نیاز مسئله، میتوان برخی از آنها را برای یافتن پاسخ استفاده کرد.
از میان روشهای مختلف، الگوریتم حریصانه یکی از روشهای پرکاربرد حل مسئله محسوب میشود که تمرکز آن بر روی پیدا کردن راهحل مسئله با کمترین هزینه است. در مطلب فعلی به توضیح الگوریتم حریصانه و ویژگیها و مزایا و معایب آن پرداختیم و مثالی کاربردی برای درک ساده آن ارائه کردیم.

