الگوریتم بهینه سازی آدام Adam — به زبان ساده

انتخاب الگوریتم بهینهسازی مناسب برای مدل یادگیری عمیق بسیار مهم است و تاثیر زیادی روی زمان رسیدن به نتیجه مطلوب دارد. الگوریتم بهینه سازی آدام (Adam Optimization Algorithm) نسخه تعمیم یافتهای از الگوریتم «گرادیان نزولی تصادفی» (Stochastic Gradient Descent | SGD) به حساب میآید که بهتازگی برای کاربردهای یادگیری عمیق در حوزه بینایی کامپیوتر و پردازش زبان طبیعی به طور گستردهتری به کار گرفته شده است. در این مقاله آموزشی، الگوریتم بهینه سازی آدام برای استفاده در یادگیری عمیق در سطح مقدماتی معرفی شده است. پس از مطالعه این مقاله، آشنایی با الگوریتم آدام، برخی از مزیتهای استفاده و نحوه عملکرد الگوریتم بهینه سازی آدام حاصل میشود. همچنین، تفاوت آن با رویکردهای مشابه و مرتبطی مثل AdaGrad و RMSProp، نحوه پیکربندی الگوریتم آدام و پارامترهای رایج در الگوریتم آدام نیز بیان خواهد شد.

الگوریتم بهینه سازی آدام چیست ؟
الگوریتم آدام یک الگوریتم بهینهسازی است که میتوان از آن به جای روش گرادیان کاهشی تصادفی کلاسیک برای بهروزرسانی وزنهای شبکه بر اساس تکرار در دادههای آموزشی استفاده کرد. الگوریتم آدام را میتوان به عنوان ترکیبی از RMSprop و گرادیان نزولی تصادفی با گشتاور (Momentum) در نظر گرفت.
الگوریتم بهینه سازی آدام توسط Diederik Kingma از شرکت OpenAI و Jimmy Ba از دانشگاه تونتو در مقالهای با عنوان «آدام: روشی برای بهینهسازی تصادفی» ارائه شد و نام آن را Adam گذاشته بودند. از این مقاله به عنوان منبع اصلی برای تدوین این مطلب استفاده شده است. نام این الگوریتم، «آدام» یا همان «Adam» است. نام Adam از عبارت «Adaptive Moment Estimation» به معنی «تخمین گشتاور تطبیقی» مشتق شده است.
- نکته: Adam مخفف هیچ عبارتی نیست و بنابراین با حروف بزرگ و به صورت «ADAM» نوشته نمیشود.
مزیت های الگوریتم بهینه سازی آدام چه هستند؟
مزیتهای جالب توجه استفاده از این الگوریتم در مسائل بهینهسازی غیر محدب در ادامه فهرست شده است:
- این الگوریتم به آسانی پیادهسازی میشود.
- الگوریتم آدام به لحاظ محاسباتی بهینه است.
- آدام به حافظه کمی نیاز دارد.
- الگوریتم بهینه سازی آدام در برابر مقیاسدهی مجدد قطری گرادیانها تغییر نمیکند و به آنها وابستگی ندارد.
- آدام برای مسائلی بسیار مناسب است که به لحاظ داده یا پارامتر بزرگ محسوب میشوند.
- لگوریتم آدام برای اهداف ناایستا (غیر ثابت | غیرمانا) مناسب است.
- آدام الگوریتم خوبی برای مسائلی است که دارای گرادیانهایی بسیار نویزدار یا تُنُک (نامتراکم) هستند.
- «اَبَرپارامترها» (Hyper-Parameters) در الگوریتم بهینه سازی آدام دارای تفسیر بصری هستند و معمولاً به تنظیم پارامتر اندکی نیاز دارند.
الگوریتم بهینه سازی آدام چگونه کار میکند؟
الگوریتم Adam با گرادیان کاهشی کلاسیک متفاوت است. گرادیان کاهشی تصادفی یک نرخ یادگیری واحد (به نام آلفا) را برای تمام بهروزرسانی وزنها حفظ میکند و این نرخ یادگیری در طول فرآیند آموزش مدل تغییر نمیکند.
- نرخ یادگیری در الگوریتم بهینه سازی آدام برای هر یک از وزنهای شبکه (پارامترها) حفظ میشود و این نرخ با شروع فرآیند یادگیری به صورت جداگانه تطبیق داده میشود.
در روش بهینه سازی آدام ، هر یک از نرخهای یادگیری برای پارامترهای مختلف از گشتاورهای اول و دوم گرادیانها محاسبه میشوند. الگوریتم Adam به عنوان نسخه ترکیبی مزیتهای دو الگوریتم تعمیمیافته دیگر گرادیان کاهشی تصادفی توصیف میشود. این دو الگوریتم در ادامه فهرست و شرح داده شدهاند:
- الگوریتم گرادیان تطبیقی (Adaptive Gradient Algorithm | AdaGrad): روشی است که نرخ یادگیری هر پارامتر را حفظ میکند. استفاده از این شیوه باعث بهبود میزان عملکرد در مسائل دارای گرادیانهای نامتراکم میشود. برای مثال میتوان به مسائل مربوط به پردازش زبان طبیعی و بینایی کامپیوتر اشاره کرد.
- الگوریتم تکثیر میانگین مربعات ریشه (Root Mean Square Propagation | RMSProp): در این روش هم نرخهای یادگیری هر پارامتر حفظ میشوند. این نرخها بر اساس میانگین مقادیر اخیر گرادیانهای مربوط به وزنها تطبیق داده شدهاند. این بدان معنا است که الگوریتم RMSProp در مسائل برخط و ناپایدار (مانند مسائل نویزدار) به خوبی کار میکند.
در الگوریتم بهینه سازی آدام ، هم مزیتهای الگوریتم AdaGrad و هم نقاط قوت الگوریتم RMSProp به کار گرفته شدهاند. در آدام به جای انطباق نرخهای یادگیری پارامترها تنها بر اساس میانگین گشتاور اول (یعنی Mean) مانند آنچه در الگوریتم RMSProp انجام شده است، از میانگین گشتاور دوم گرادیانها (واریانس غیر مرکزی) هم استفاده میشود. الگوریتم آدام منحصراً میانگین متحرک نمایی گرادیان و گرادیان مربعات را محاسبه میکند و پارامترهای beta1 و beta2 نرخ فروپاشی (خرابی) این میانگینهای متحرک را کنترل میکنند.
مقدارهای اولیه میانگینهای متحرک و مقادیر beta1 و beta2 نزدیک به عدد یک (مقدار توصیه شده)، به اختلاف معیار تخمینهای گشتاورهایی به سمت صفر منتج میشود. در بخش بعدی، کارآمد بودن یا نبودن الگوریتم بهینه سازی آدام مورد بررسی قرار گرفته است.
آیا الگوریتم بهینه سازی آدام موثر و کارآمد است؟
Adam الگوریتمی محبوب در حوزه یادگیری عمیق به حساب میآید؛ چرا که با استفاده از آن میتوان خیلی سریع به نتایج بهینه و مطلوب دست پیدا کرد. نتایج تجربی نشان میدهد که الگوریتم آدام در عمل به خوبی کار میکند و در مقایسه با سایر روشهای بهینهسازی تصادفی عملکرد مطلوبی دارد.
در مقاله اصلی، الگوریتم آدام به صورت عملی و تجربی مورد آزمایش قرار گرفته است تا نشان داده شود که همگرایی این الگوریتم، انتظارات تجزیه-تحلیلهای تئوری را برآورده میکند. در مقاله اصلی، الگوریتم آدام روی موارد زیر پیادهسازی شده است:
- رگرسیون لجستیک (logistic regression) با مجموعه داده MNIST (مخصوص تشخیص ارقام)
- رگرسیون لجستیک با مجموعه داده IMDB (مخصوص تجزیه-تحلیل احساسات)
- الگوریتم پرسپترون چند لایه (Multilayer Perceptron) با مجموعه داده MNIST
- شبکه عصبی پیچشی (Convolutional Neural Networks) با مجموعه داده CIFAR-10 (مربوطه به بازشناسی تصویر)
نویسندگان مقاله اصلی از اجرای الگوریتم بهینه سازی آدام روی موارد فوق اینگونه نتیجهگیری کردهاند:
با آزمایش روی مدلها و مجموعه دادههای بزرگ، مشخص میشود که الگوریتم بهینه سازی آدام به لحاظ عملی در حل مسائل یادگیری عمیق به صورت بهینه عمل میکند.
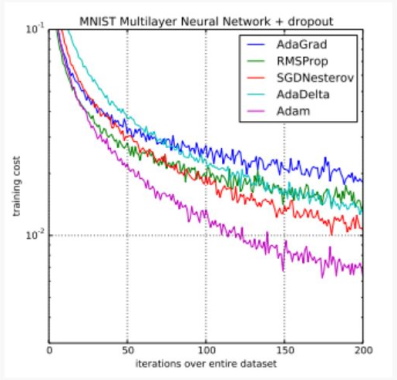
تصویر فوق مقایسه الگوریتم آدام با الگوریتمهای بهینهسازی دیگر آموزش یک پرسپترون چند لایه را نشان میدهد. این تصویر برگرفته از مقاله اصلی است و با استفاده از مدلها و مجموعه دادههای بزرگ نشان میدهد که الگوریتم آدام میتواند به طور کارآمدی مسائل یادگیری عمیق عملی را حل کند.
«سباستین رودر» (Sebastian Ruder)، بررسی جامعی از الگوریتمهای بهینهسازی گرادیان نزولی مدرن را با عنوان «مروری بر الگوریتمهای بهینهسازی گرادیان کاهشی» ارائه کرده است که در ابتدا به صورت یک پست وبلاگی و سپس به عنوان یک گزارش فنی در سال ۲۰۱۶ منتشر شده است. در این مقاله اساساً به بررسی روشهای مدرن پرداخته شده است. در بخشی از این مقاله با عنوان «از کدام بهینهساز استفاده کنیم؟» الگوریتم بهینه سازی آدام را پیشنهاد کرده است:
تا اینجا اینگونه برداشت میشود که Adadelta ،RMSprop و آدام الگوریتمهای بسیار مشابهی هستند که در شرایط مشابه به خوبی عمل میکنند. اصلاح اختلاف معیار آدام به آن کمک میکند تا این اگوریتم با کم شدن تراکم گرادیانها در پایان بهینهسازی کمی بهتر از الگوریتم RMSprop عمل کند. تا این لحظه، به طور کلی میتوان الگوریتم بهینه سازی آدام را به عنوان بهترین انتخاب در نظر گرفت.
در دوره آموزشی یادگیری عمیق برای بینایی کامپیوتری دانشگاه استنفورد (دوره CS231n) که توسط Andrej Karpathy و همکارانش ارائه شده است، باز هم استفاده از الگوریتم آدام به عنوان روش بهینهسازی پیشفرض برای کاربردهای یادگیری عمیق توصیه شده است:
در عمل، الگوریتم آدام فعلاً به عنوان الگوریتم پیشفرض برای استفاده پیشنهاد میشود. این الگوریتم معمولاً کمی بهتر از RMSProp عمل میکند. اگرچه، به هر حال اغلب ارزشش را دارد که الگوریتم گرادیان کاهشی تصادفی به همراه گشتاور نستروف (Nesterov Momentum) هم امتحان شود.
همچنین در ادامه دوره آموزشی استنفورد با وضح بیشتری اینگونه توضیح داده شده است:
دو بهروزرسانی که توصیه میشود از آنها استفاده کنید، الگوریتمهای SGD+Nesterov Momentum یا آدام هستند.
علاوه بر این، الگوریتم آدام برای بنچمارکهایی (سنجههایی) در مقالههای علمی یادگیری عمیق مورد استفاده قرار میگیرد. برای مثال، الگوریتم بهینه سازی آدام در دو مقاله زیر استفاده شده است.
- تولید کننده زیرنویس تصویر با استفاده از توجه دیداری با تمرکز بر حوزه زیرنویس تصویر (Image Captioning) | Show, Attend and Tell: Neural Image Caption Generation with Visual Attention | [+]
- مقاله DRAW یک شبکه عصبی بازگشتی برای تولید تصویر | DRAW: A Recurrent Neural Network For Image Generation | [+]
بنابراین، میتوان به این نتیجه رسید که الگوریتم آدام عملکرد مطلوبی دارد و استفاده از آن در اکثر مواقع نتایج بهتری را نسبت به سایر الگوریتمها تولید میکند. در صورتی که مثالهای دیگری از عملکرد مطلوب الگوریتم بهینه سازی آدام سراغ دارید، آنها را در کامنتها با ما در میان بگذارید.
پارامترهای پیکربندی الگوریتم بهینه سازی آدام
الگوریتم بهینه سازی آدام دارای چهار پارامتر پیکربندی اصلی است که هر یک از آنها در ادامه فهرست شدهاند:
- alpha: با عنوان «نرخ یادگیری» یا «طول گام» نیز از آن یاد میشود. آلفا نسبتی است که وزنها بر اساس آن بهروزرسانی میشوند (به عنوان مثال ۰.۰۰۱). مقادیر بزرگتر برای پارامتر alpha (مثلاً ۰.۳) باعث میشود یادگیری اولیه سریعتر و پیش از آن انجام شود که میزان نرخ مربوطه بهروزرسانی میشود. مقادیر کوچکتر برای پارامتر آلفا (به عنوان مثال 1.0E-5) در طول آموزش، سرعت یادگیری را کاهش میدهد.
- beta1: نرخ فروپاشی نمایی برای تخمینهای گشتاور اول است (مثلاً مقدار آن میتواند ۰.۹ باشد).
- beta2: نرخ فروپاشی نمایی برای تخمینهای لحظه دوم است (مثلاً مقدار آن میتواند ۰.۹ باشد). این مقدار باید در مسائلی با گرادیان تُنُک (مانند NLP و مسائل بینایی کامپیوتر) نزدیک به یک باشد.
- epsilon: عددی بسیار کوچکی (مانند 10E-8) است که در پیادهسازیها برای جلوگیری از تقسیم بر صفر استفاده میشود.
علاوه بر این، کاهش نرخ یادگیری نیز میتواند با الگوریتم آدام استفاده شود. در مقاله اصلی از نرخ خرابی alpha = alpha/sqrt(t) استفاده میشود که هر دوره (t) را برای نمایش رگرسیون لجستیک بهروزرسانی میکند. مقاله اصلی، در خصوص تنظیمات پیشفرض اینگونه توضیح میدهد:
تنظیمات پیشفرض مناسب برای مسائل تست شده یادگیری ماشین به صورت beta2=۰.۹۹۹ ،alpha=۰.۰۰۱ و epsilon= 1e-8
در مستندات TensorFlow برخی تنظیمات برای پارامتر اپسیلون پیشنهاد شده است:
به طور کلی مقدار پیشفرض 1e-8 برای اپسیلون ممکن است نتایج خوبی را تولید نکند. برای مثال، زمان آموزش یک شبکه Inception در ImageNet یک انتخاب خوب برای پارامتر اپسیلون میتواند مقدار یک یا ۰.۱ باشد.
میتوان ملاحظه کرد که کتابخانههای محبوب و رایج یادگیری عمیق عموماً از پارامترهای پیشفرض توصیه شده در مقاله استفاده میکنند:
- پارامترهای پیشفرض در کتابخانه TensorFlow:
- learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08
- پارامترهای پیشفرض کتابخانه Keras:
- lr=0.001, beta_1=0.9, beta_2=0.999, epsilon=1e-08, decay=0.0.
- پارامترهای پیشفرض Blocks:
- learning_rate=0.002, beta1=0.9, beta2=0.999, epsilon=1e-08, decay_factor=1.
- Lasagne:
- learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08
- Caffe:
- learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08
- MxNet:
- learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8
- Torch:
- learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-8
به این ترتیب مباحث کلیدی پیرامون اپلیکیشن بهینه سازی آدام تا اینجا ارائه شدند، حال در ادامه برای یادگیری بیشتر، مجموعه دورههای آموزش الگوریتمهای بهینه سازی هوشمند تم آف به علاقهمندان معرفی شده است و پس از آن نیز بیشتر به الگوریتم آدام پرداخته خواهد شد.
ویژگی های الگوریتم بهینه سازی آدام چه هستند؟
در این بخش از مقاله برخی از ویژگیهای الگوریتم بهینه سازی آدام فهرست شدهاند:
- طول گام واقعی برداشته شده توسط آدام در هر تکرار تقریباً به ابرپارامتر طول گام محدود شده است. این ویژگی درک بصری را به ابرپارامتر نرخ یادگیری غیر بصری قبلی اضافه میکند.
- طول گام قاعده بهروزرسانی آدام نسبت به مقدار گرادیان تغییری نمیکند که هنگام عبور از نواحی با گرادیان کوچک (مانند پایینترین نقاط بین دو قله یا درهها) کمک زیادی میکند.
- الگوریتم بهینه سازی آدام برای ترکیب مزایای Adagrad که به خوبی با گرادیانهای پراکنده کار میکند و الگوریتم RMSprop که در تنظمیات برخط به خوبی کار میکند، طراحی شده است. وجود این قابلیتها در الگوریتم آدام کمک میکند که از این الگوریتم برای طیف وسیعتری از کارها استفاده شود. همچنین میتوان به الگوریتم آدام به عنوان ترکیبی از دو الگوریتم RMSprop و SGD با گشتاور نگاه کرد.
معایب الگوریتم بهینه سازی آدام کدامند؟
الگوریتم آدام دارای مشکلاتی است که منجر به کاهش محبوبیت آن شده است. هنگامی که الگوریتم آدام برای اولین بار معرفی شد، متخصصان در برابر قدرت آن بسیار شگفتزده شدند. همانطور که پیشتر به آن پرداخته شد، مقالهای که الگوریتم آدام در آن معرفی شده حاوی برخی از نمودارهای بسیار خوشبینانهای است که دستاوردهای عملکردی بزرگی از نظر سرعت آموزش در آن نشان داده شده است.
سپس مقاله Nadam نمودارهایی را ارائه کرد که حتی نتایج بهتری را نشان میداد. این نمودارها در بخش زیر آمدهاند:
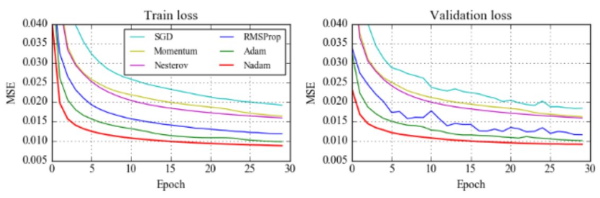
با این حال، پس از مدتی متخصصان متوجه شدند که علیرغم زمان آموزش بالاتر، الگوریتم آدام در برخی نواحی به یک راه حل بهینه همگرا نمیشود، بنابراین، نتایج پیشرفتهتر برای برخی اهداف (مانند طبقهبندی تصویر روی پایگاه داده محبوب CIFAR) همچنان تنها با به کارگیری الگوریتم گرادیان کاهشی تصادفی به همراه گشتاور به دست میآید.
ویلسون و همکارانش در مقاله خود با عنوان «ارزش کم روش گرادیان تطبیقی در یادگیری ماشین» به طور دقیقتری نشان دادند که روشهای تطبیقی (مانند آدام یا Adadelta) هنگام تست روی مجموعه گوناگونی از وظایف یادگیری عمیق به خوبی روش گرادیان کاهشی تصادفی با گشتاور تعمیم نمییابد و این مقاله متخصصان را برای استفاده از این الگوریتمهای بهینهسازی محبوب دلسرد کرد. پس از آن، تحقیقات زیادی برای تجزیه و تحلیل تعمیم ضعیف آدام انجام شد که تلاش میکرد آدام را به سمتی ببرد که اختلاف زیاد آن با الگوریتم گرادیان کاهشی تصادفی کاهش یابد.
محققانی به نام Nitish Shirish Keskar و Richard Socher در مقالهای با عنوان «بهبود عملکرد تعمیم با تغییر آدام به گرادیان کاهشی تصادفی» نشان دادند که در طول یادگیری با تغییر الگوریتم به گرادیان کاهشی تصادفی توانستهاند نسبت به زمانی که فقط از الگوریتم آدام استفاده میکنند به قدرت تعمیم بهتری برسند. آنها راهحل سادهای را پیشنهاد کردند که از ایده بسیار سادهای استفاده میکرد. آنها متوجه شدند که در گامهای اولیه آموزش باز هم آدام عملکرد بهتری نسبت به گرادیان کاهشی تصادفی دارد، اما در ادامه یادگیری اشباع میشود. آنها خط مشی سادهای را با نام «SWATS» پیشنهاد کردند. در این استراتژی، آنها آموزش شبکه عصبی عمیق را با الگوریتم آدام شروع کردند، اما هنگامی که به معیارهای خاص و معینی رسیدند، الگوریتم را به گرادیان کاهشی تصادف تغییر دادند. آنها موفق شدند به نتایج قابل مقایسهای با گرادیان کاهشی تصادف به همراه گشتاور دست پیدا کنند.
همگرایی الگوریتم بهینه سازی آدام
یکی از موارد مهم در خصوص پیدا کردن نقطه ضعف الگوریتم آدام، تجزیه و تحلیل همگرایی آن است. نویسندگان در مقاله اصلی، ثابت کردند که الگوریتم آدام در شرایط محدب به کمینه سراسری همگرا میشود. با این حال، چندین مقاله پی بردند که اثبات آنها چند اشکال دارد. Block و همکارانش ادعا کردند که خطاهایی را در تجزیه و تحلیل همگرایی اصلی پیدا کردهاند اما همچنان ثابت کردند که الگوریتم همگرا میشود و پیرامون این موضوع در مقاله خود اثبات هم ارائه کردهاند.
مقاله اخیر دیگری از کارمندان گوگل در ICLR 2018 منتشر و حتی برنده جایزه بهترین مقاله هم شد. برای این که به صورت عمیقتری به آن مقاله پرداخته شود، ابتدا باید چارچوب استفاده شده برای اثبات همگرایی آدام در توابع محدب توضیح داده شود.
چارچوب استفاده شده برای اثبات همگرایی آدام در توابع محدب
در سال ۲۰۰۳ مارتین زینکویچ مسئله «برنامه نویسی محدب برخط» (Online Convex Programming) را معرفی کرد. در تنظیمات ارائه شده، دنبالهای از توابع محدب c2 ،c1 و توابع دیگر وجود دارد (تابع هزینه در دسته کوچک iام در مورد بهینه سازی یادگیری عمیق اجرا میشود). این الگوریتم که مشکل آدام را در هر برچسب زمانی t حل میکند، یک نقطه x[t] انتخاب میکند (پارامتر مدل) و سپس تابع هزینه c را برای برچسب زمانی فعلی به دست میآورد. برای درک این که چقدر الگوریتم خوب کار میکند، میزان پشیمانی (Regret) الگوریتم پس از T دوره به صورت زیر تعریف شده است:
$$R(T)=sum^T_{t=1}[c_t(w_t)-c_t(w^*_t)]$$
در فرمول بالا، R نماد پشیمانی (regret | تأسف)، c تابع هزینه روی دسته کوچک tام، w بردار پارامترهای مدل (وزن) و $$ w^* $$ مقدار بهینه بردار وزن محسوب میشود. در اینجا، هدف اثبات این است که پشیمانی الگوریتم برابر با $$ R(T) = O(T) $$ یا کمتر از آن است؛ به این معنی که به طور متوسط همگرایی مدل به یک راه حل بهینه همگرا میشود.
مارتین زینکوویچ (Martin Zinkevich) در مقالهاش ثابت کرده که گرادیان نزولی با استفاده از ویژگی توابع محدب به راهحل بهینه در تنظیمات همگرا میشود. ویژگی شناخته شده توابع محدب به صورت زیر است:
$$c_t(x)geq(triangledown c_t(x_t))(x-x_t)+c_t(x_t)$$
خالقان Adam از چارچوب و رویکرد مشابهی استفاده کردهاند تا اثبات کنند که الگوریتم آنها به یک راهحل بهینه همگرا میشود. Reddi و همکاران او نیز چندین اشتباه در اثبات آنها مشاهده کردند که یکی از اصلیترین این اشکالات در مقدار است. این اشتباه هم در مقاله اثبات همگرایی آدام و مقالات بهبود اثبات همگرایی آدام وجود دارد:
$$frac{V_{t+1}}{eta_{t+1}}-frac{V_t}{eta_t}$$
در رابطه فوق، $$ V $$ به عنوان یک تابع انتزاعی تعریف شده است که برای پارامترهایی که برای هر الگوریتم منحصر به فرد متفاوت است، نرخ یادگیری را مقیاسبندی میکند. این مقدار (V) برای الگوریتم آدام، میانگینهای متحرک گرادیانهای مربعات گذشته آن، برای الگوریتم Adagrad، جمع تمام گرادیانهای فعلی و گذشته آن و برای گرادیان کاهشی تصادفی، فقط مقدار یک میشود. نویسندگان پی برند که برای این که مبحث را اثبات کنند، این مقدار باید مثبت باشد. به راحتی میتوان متوجه شد که برای الگوریتمهای SGD و Adagrad این مقدار همواره مثبت است، اما برای الگوریتم Adam (یا RMSprop) مقدار V میتواند به طور غیر قابل منتظرهای عمل کند. در آنها مثالی ارائه کردند که نشان میدهد الگوریتم آدام نمیتواند همگرا شود. این مثال در ادامه آورده شده است:
$$f_t(x)={C_x for t mod 3=3 , -x, otherwise$$
$$
f_{t}(x)=left{begin{array}{c}
C x text { for } mathrm{t} text { mod } 3=3 \
-x, text { otherwise }
end{array}right.
$$
الگوریتم آدام برای اثبات فوق با شکست مواجه میشود. برای این دنباله جواب بهینه x = -1 است، ولی الگوریتم آدم به جواب بهینه محلی یک همگرا میشود و در این مورد الگوریتم آدام نتوانسته به جواب بهینه سراسری برسد. الگوریتم هر ۳ مرحله یکبار، گرادیان بزرگ C را به دست میآورد در حالی که دو مرحله دیگر گرادیان ۱- را نتیجه میدهد که الگوریتم در جهت اشتباه حرکت میکند. از آنجایی که اکثر اوقات، مقادیر طول گام در طی زمان کاهش مییابد، آنها راهحل حفظ بیشینه مقادیر V را پیشنهاد کردند و آن را به جای میانگین متحرک برای بهروزرسانی پارامترها استفاده کردند. الگوریتم به دست آمده Amsgrad نامیده شد. در ادامه پیادهسازی این الگوریتم انجام شده است که نشان میدهد الگوریتمهای مختلفی روی دنباله تابعی که در بالا مطرح شد، همگرا میشوند.
for t in range(num_iterations):
g = compute_gradient(x, y)
m = beta_1 * m + (1 - beta_1) * g
v = beta_2 * v + (1 - beta_2) * np.power(g, 2)
v_hat = np.maximum(v, v_hat)
w = w - step_size * m / (np.sqrt(v_hat) + epsilon)کد فوق برای الگوریتم بدون اصلاح کردن اختلاف معیار پیادهسازی شده است.
آدام چقدر در مواجهه با دادههای دنیای واقعی کمککننده است؟ تقریباً میتوان گفت که متأسفانه الگوریتمی که به نتایجی بهتر از آدام دست پیدا کند هنوز موجود نیست. بعضی از محققان آزمایشهایی را روی Amsgrad انجام دادند که نتایج آن مشابه با الگوریتم آدام بود. در بعضی از آزمایشهای دیگر نتایج نشان دادهاند که Amsgrad حتی بدتر از آدام عمل میکند. به طور کلی این امکان نیز وجود دارد که مشکل از الگوریتم آدام نباشد بلکه به علت چارچوب توضیح داده شده برای تجزیه و تحلیل همگرایی باشد که امکان تنظیم بیش از حد ابرپارامترها را فراهم نمیکند.
کاهش وزن با الگوریتم بهینه سازی آدام
یکی از مواردی که به آدام بسیار کمک کرد، مقاله اصلاح منظمسازی (تنظیم | Regularization) کاهش وزن در آدام بود. در این مقاله، ابتدا نشان داده شده است که علیرغم باور رایج، منظمسازی L2 (که به آن Norm l2 یا Ridge هم گفته میشود) با کاهش وزن نیست.
اگر چه برای گرادیان کاهشی تصادفی، منظمسازی L2 معادل کاهش وزن است و با یکدیگر برابر هستند. روشی کاهش وزن که در سال ۱۹۸۸ معرفی شد به شرح زیر است:
$$w_{t+1}=(1-lambda)w_t-etatriangledown f_t(w_t)$$
در فرمول فوق، نماد λ که به آن لامبدا (Lambda) میگویند، ابرپارامتر کاهش وزن برای تنظیم محسوب میشود. کاهش وزن در آخرین گام هنگام بهروزرسانی وزن اعمال میشود و وزنهای بزرگ را جریمه میکند. روشی که به طور مرسوم برای SGD پیادهسازی میشود از طریق تنظیم L2 است. در ادامه تابع هزینه تغییر داده میشود تا نرم L2 بردار وزن را شامل شود. عبارت تغییر داده شده به صورت زیر است:
$$f^{reg}_t(w_t)=f_t(w_t)+frac{lambda}{2}||w_t||^2_2$$
از نظر تاریخی، روشهای گرادیان نزولی تصادفی این روش پیادهسازی تنظیم کاهش وزن را به ارث بردهاند، همین طور آدام نیز این روش را از SGD به ارث برده است. با این حال، تنظیم L2 برای آدام معادل با کاهش وزن نیست. هنگام استفاده از تنظیم L2، جریمهای برای وزنهای بزرگ استفاده میشود که از طریق میانگین متحرک گرادیانهای مربع فعلی و گذشته مقیاسبندی میشود. بنابراین وزنهایی با اندازه گرادیان معمولی بزرگ با مقدار نسبی کوچکتری از وزنهای دیگر منظم میشوند. در مقابل، کاهش وزن همه وزنها را از طریق عامل یکسانی منظم میکند. برای استفاده از کاهش وزن برای آدام، نیاز است که قاعده بهروزرسانی به صورت زیر تغییر کند:
$$w_t=w_{t-1}-eta(frac{hat{m}}{sqrt{hat{v}_t}+in}+lambda w_{t-1})$$
ظابطه فوق برای بهروزرسانی آدام با کاهش وزن است. از این طریق نشان داده شد که این انواع تنظیم متفاوتی برای آدام وجود دارد. همچنین محققان نشان دادند که آدام با هر دوی آنها خوب کار میکند. تفاوت این روشها به خوبی در نمودارهای زیر نشان داده شده است:
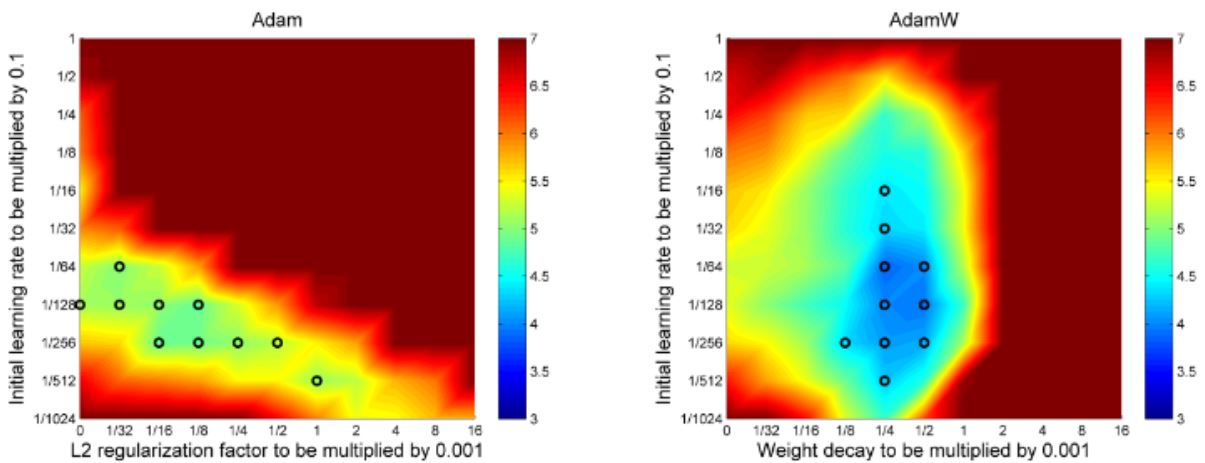
این نمودارها ارتباط بین نرخ یادگیری و روش تنطیم را نشان میدهند. رنگ در این نمودارها نشاندهنده کم یا زیاد بودن خطای تست (آزمون) برای هر دو ابرپارامتر است. همان طور که در نمودارها مشخص است، الگوریتم آدام علاوه بر این که با کاهش وزن خطای آزمون بسیار کمتری را دریافت میکند بلکه در عمل به جداسازی نرخ یادگیری و تنظیم ابرپارامتر نیز کمک میکند. در تصویر سمت چپ میتوان گفت در صورتی که پارامترها، به عنوان مثال نرخ یادگیری تغییر یابد، برای رسیدن به نقطه بهینه دوباره باید عامل L2 نیز تغییر داده شود که نشان میدهد این دو پارامتر به یکدیگر وابسته هستند. این وابستگی باعث میشود که گاهی اوقات تنظیم ابرپارامترها بسیار دشوار شود. در تصویر سمت راست نیز مشاهده میشود، چنانچه تا زمانی که در محدودهای از مقادیر بهینه برای یک پارامتر باقی ماند، میتوان پارامتر دیگر را به طور مستقل تغییر داد.
تحقیقات دیگری نشان میدهد که مقدار بهینه به کار رفته برای کاهش وزن در واقع به تعداد تکرار در طول آموزش وابسته است. برای مقابله با این عمل، یک فرمول تطبیقی ساده برای تنظیم کاهش وزن پیشنهاد شد که به صورت زیر است:
$$ lambda=lambda_{norm}sqrtfrac{b}{BT}$$
در فرمول فوق، b اندازه دسته، B تعداد کل نقاط اموزش در هر دوره و T تعداد کل دورهها محسوب میشود. این فرمول هایپر پارامتر لاندا را با یک لاندای نرمالسازی شده جدید جایگزین میکند. قبلاً الگوریتم آدام خیلی از SGD عقب بود. اما با کاهش وزن جدید، آدام با شروع مجدد نتایج بسیار بهتری را به دست آورد. اما هنوز به خوبی SGDR نیست.
گشتاور چیست ؟
گشتاور Nام یک متغیر تصادفی به عنوان مقدار مورد انتظار آن متغیر به توان n تعریف میشود. رابطه آن در ادامه آمده است:
$$m_n=E[X^n]$$
در فرمول بالا، m نماد گشتاور (Moment | لحظه) و X نماد متغیر تصادفی است. گرادیان تابع هزینه شبکه عصبی را میتوان به عنوان یک متغیر تصادفی در نظر گرفت. زیرا معمولاً روی برخی از دستههای تصادفی کوچکی از دادهها ارزیابی میشود. مومنت اول میانگین است و مومنت دوم واریانس غیر مرکزی (به این معنی که میانگین در طول محاسبه واریانس کم نمیشود) محسوب میشود. حال باید با نحوه به دست آوردن این مقادیر آشنا شد، سپس چگونگی استفاده از این مقادیر مطرح خواهد شد.
برای تخمین مومنتها، الگوریتم بهینه سازی Adam میانگینهای متحرک نمایی را استفاده میکند که بر روی گرادیان ارزیابی شده روی یک دسته کوچک فعلی محاسبه میشوند. معادله آن به صورت زیر است:
$$m_t=beta_1m_{t-1}+(1-beta_1)g_t$$
$$v_t=beta_2v_{t-1}+(1-beta_2)g^2_t$$
فرمول فوق برای میانگین متحرک گرادیان و گرادیان مجذور است. در این فرمول، m و v میانگینهای متحرک، g گرادیان روی دسته کوچک فعلی محسوب میشود. بتاها، ابرپارامتر جدید معرفی شده الگوریتم است و آنها مقادیر پیشفرض واقعاً خوبی دارند که به ترتیب 0.9 و 0.999 هستند. میتوان گفت تقریباً هیچ کس هرگز این موارد را تغییر نمیدهد. بردارهای میانگین متحرک در تکرار اول با صفر مقداردهی میشوند. در معادله اول، نحوه ارتباط مقادیر با مومنت تعریف شده است. از آنجایی که m و n تخمینهای مومنت اول و دوم هستند، نیاز است که ویژگیهای زیر وجود داشته باشد:
$$E[m_t]=E[g_t]$$
$$E[v_t]=E[g^2_t]$$
مقادیر مورد انتظار تخمینگرها باید مساوی پارامتری باشند که قصد تخمین آن وجود دارد، چنانچه این اتفاق بیفتد، پارامتر نیز مقدار مورد انتظار محسوب میشود. اگر این ویژگیها درست باشند به این معنی است که تخمینگرهایی بدون اختلاف معیار وجود دارد. اکنون قابل مشاهده است که این موارد برای میانگین متحرکهای روش ذکر شده صادق نیستند. از آنجایی که در این روش، میانگینها با صفر مقداردهی اولیه شدند، تخمینگرها با اختلاف معیار نزدیک به صفر هستند. حال در ادامه برای m اثبات میشود. به علت این که اثبات v مشابه با اثبات m است از آن صرفنظر میشود. برای اثبات آن باید برای m تا گرادیان اول فرمولی نوشت. در ادامه برای مشاهده الگویی که قرار است استفاده شود، مقادیر چند m باز میشود:
$$m_0=0$$
$$m_1=beta_1m_0+(1-beta_1)g_1=(1-beta_1)g_1$$
$$m_2=beta_1m_1+(1-beta_1)g_2=beta_1(1-beta_1)g_1+(1-beta_1)g_2$$
$$m_3=beta_1m_2+(1-beta_1)g_3=beta^2_1(1-beta_1)g_1+beta_1(1-beta_1)g_2+(1-beta_1)g_3$$
همان طور که در اثبات فوق قابل مشاهده است، هر چقدر که مقدار m بیشتر گسترش داده شود، مقادیر اولیه گرادیانها کمتر به مقدار کلی کمک میکنند، زیرا آنها در بتای کوچکتر و کوچکتری ضرب میشوند. با به دست آوردن این الگو، میتوان فرمول میانگین متحرک را به صورت زیر بازنویسی کرد:
$$m_t=(1-beta_1)sum^t_{i=0}beta^{t-i}_1g_i$$
اکنون با ملاحظه مقدار موردانتظار m و چگونگی ارتباط درست آن با مومنت اول، اختلاف این دو به صورت زیر اصلاح میشود:
$$E[m_t]=E[(1-beta_1)sum_{i=1}^tbeta^{t-i}_1g_i]$$
$$=E[g_i](1-beta_1)sum_{i=1}^tbeta^{t-i}_1+zeta$$
$$=E[g_i](1-beta_1^t)+zeta$$
فرمول فوق، اصلاح اختلاف معیار برای تخمینگر مومنت اول است. در سطر اول، از فرمول جدیدی برای میانگین متحرک استفاده شده تا m را گسترش دهد. سپس $$g[i] $$ با $$g[t] $$ تقریب زده میشود. حال میتوان آن را از مجموع خارج کرد، زیرا اکنون به i وابستگی ندارد. از آنجایی که تقریب در حال جایگذاری است در فرمول خطای C ظاهر میشود. در خط آخر، فرمول فقط برای جمع سریهای هندسی محدود استفاده شده است. دو نکته قابل توجه در معادله وجود دارد که در بخش زیر مطرح شدهاند:
- تخمینگر اختلاف معیار شده در معادله وجود دارد. این فقط برای آدام صحیح نیست در حالی که همین معادله برای الگوریتمها با استفاده از میانگینهای متحرک (SGD با گشتاور، RMSprop و موارد دیگر) صدق میکند.
- این تاثیر زیادی نخواهد داشت، مگر این که درخواست آموزش باشد، زیرا مقدار بتا به توان t با سرعت به سمت صفر میرود.
حال باید تخمینگر اصلاح شود تا مقدار مورد انتظار همانی باشد که مدنظر است. معمولاً این گام به عنوان اصلاح اختلاف معیار شناخته میشود. فرمول نهایی برای این تخمینگر به صورت زیر خواهد بود:
$$hat{m}_t=frac{m_t}{1-beta^t_1}$$
$$hat{v}_t=frac{v_t}{1-beta^t_2}$$
فرمولهای فوق برای تخمینگرهای اصلاح شده اختلاف معیار گشتاورهای اول و دوم هستند. تنها چیزی باید انجام شود این است که از آن میانگینهای متحرک استفاده شود تا نرخ یادگیری به طور منحصر به فردی برای هر پارامتر مقیاس شود. روشی که در آدام انجام میشود بسیار ساده است، برای بهروزرسانی کردن وزن موارد زیر انجام میشود:
$$w_t=w_{t-1}-etafrac{hat{m}_t}{sqrt{hat{v}_t}+in}$$
در فرمول بالا، w وزن مدل و نماد اتا (η | Eta) طول گام (میتواند به تکرار وابسته باشد) محسوب میشود. این قاعده بهروزرسانی برای آدام است. برای بعضی از افراد درک چنین مفاهیمی در کد میتواند آسانتر باشد. در ادامه پیادهسازی آدام در پایتون تا حد امکان آورده شده است:
for t in range(num_iterations):
g = compute_gradient(x, y)
m = beta_1 * m + (1 - beta_1) * g
v = beta_2 * v + (1 - beta_2) * np.power(g, 2)
m_hat = m / (1 - np.power(beta_1, t))
v_hat = v / (1 - np.power(beta_2, t))
w = w - step_size * m_hat / (np.sqrt(v_hat) + epsilon)دو تغییر کوچک در Adam وجود دارد که در فریمورکهای یادگیری عمیق پیادهسازی شدهاند و در ادامه به اختصار به آنها پرداخته میشود:
تغییر اول به نام آدامکس (Adamax) که توسط نویسنده آدام در همین مقاله معرفی شده بود. ایده آدامکس این است که مقدار v به عنوان نُرم L2 از گرادیانهای گذشته و فعلی در نظر گرفته شود. میتوان آن را به قاعده بهروزرسانی Lp تعمیم داد، اما برای مقادیر بزرگ p بسیار ناپایدار میشود. اما اگر از حالت خاص نُرم L-infinity استفاده شود، الگوریتمی بسیار پایدار و با عملکرد بسیار خوب را نتیجه میدهد. در ادامه نحوه پیادهسازیAdamax با پایتون آمده است:
for t in range(num_iterations):
g = compute_gradient(x, y)
m = beta_1 * m + (1 - beta_1) * g
m_hat = m / (1 - np.power(beta_1, t))
v = np.maximum(beta_2 * v, np.abs(g))
w = w - step_size * m_hat / vتغییر دوم: درک تغییر دوم که الگوریتم بهینه سازی نادام (Nadam) نام دارد، کمی سختتر است. این الگوریتم توسط Timothy Dozat در مقاله «پیوستن گشتاور Nesterov به آدام» منتشر شد. همان طور که از نام آن مشخص است، این ایده برای استفاده از اصطلاح گشتاور نستروف (Nesterov) برای اولین میانگینهای متحرک است. در ادامه قاعده بهروزرسانی SGD با گشتاور ذکر شده است:
$$m_t=beta m_{t-1}+eta g_t$$
$$w_t=w_{t-1}-m_t=w_{t-1}-beta m_{t-1}-eta g_t$$
فرمول فوق، قاعده بهروزرسانی SGD با گشتاور است. در فرمول بالا مشاهده میشود که قاعده بهروزرسانی معادل با برداشتن گامی در جهت بردار گشتاور و سپس برداشتن گامی در جهت گرادیان است. با این حال، گام گشتاور به گرادیان فعلی وابسته نیست، بنابراین میتوان از طریق بهروزرسانی پارامترها با گام گشتاور قبل از محاسبه گرادیان، جهت گام گرادیان با کیفیت بالاتری را به دست آورد. برای دستیابی به آن، نیاز است که بهروزرسانی به صورت زیر تغییر پیدا کند:
$$g_t=triangledown f(w_{t-1}-beta m_{t-1})$$
$$m_t = beta m_{t-1}+eta g_t$$
$$w_t = w_{t-1}-m_t$$
در فرمول فوق، f نماد تابع هزینه برای بهینهسازی محسوب میشود. بنابراین با گشتاور شتاب نستروف، ابتدا پرشی بزرگ در جهت گرادیان فراهم شده قبلی انجام میشود و سپس گرادیانی که در انتها به آن رسیده اندازهگیری میشود تا اصلاح صورت بگیرد. در ادامه تصویری برای تجسم این موارد آورده شده است:
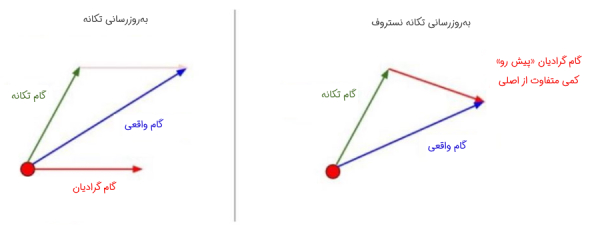
همین روش را میتوان از طریق تغییر اولین میانگین متحرک به گشتاور شتاب نستروف در الگوریتم بهینه سازی آدام ترکیب کرد. یک ترفند محاسباتی را میتوان در اینجا به کار برد:
به جای بهروزرسانی پارامترها برای ایجاد گام گشتاور و تغییر مجدد، میتوان همان نتیجه را از طریق فقط یکبار به کار بردن گام گشتاور مرحله زمانی t + 1 در طی بهروزرسانی گام زمانی قبلی t به جای t+1 به دست آورد. با استفاده از این ترفند، پیادهسازی Nadam ممکن است به صورت زیر باشد:
for t in range(num_iterations):
g = compute_gradient(x, y)
m = beta_1 * m + (1 - beta_1) * g
v = beta_2 * v + (1 - beta_2) * np.power(g, 2)
m_hat = m / (1 - np.power(beta_1, t)) + (1 - beta_1) * g / (1 - np.power(beta_1, t))
v_hat = v / (1 - np.power(beta_2, t))
w = w - step_size * m_hat / (np.sqrt(v_hat) + epsilon)جمعبندی
در این مقاله آموزشی به معرفی و شرح الگوریتم بهینهسازی آدام پرداخته شد. الگوریتم آدام قطعاً یکی از بهترین الگوریتمهای بهینهسازی برای یادگیری عمیق محسوب میشود و محبوبیت آن به سرعت در حال افزایش است. درست است که محققان متوجه مشکلاتی در استفاده از الگوریتم Adam در نواحی خاص شدهاند، اما در حال کار روی راهحلها هستند تا بتوانند نتایج آدام را بهبود دهند.
Adam یک الگوریتم بهینهسازی جایگزین برای گرادیان کاهشی تصادفی برای آموزش مدلهای یادگیری عمیق است. این الگوریتم بهترین ویژگیهای الگوریتمهای AdaGrad و RMSProp را ترکیب میکند و یک الگوریتم بهینهسازی ارائه میدهد که میتواند گرادیانهای پراکنده را در مسائل نویزدار مدیریت کند. در این مقاله دورههای آموزشی مرتبط با بهینه سازی هوشمند و یادگیری ماشین نیز برای یادگیری سایر مباحث بهینه سازی معرفی شدهاند.

