پیاده سازی اندیکاتور ایچیموکو در پایتون — راهنمای گام به گام

ارسال شده توسط

itsme

در 18 آبان, 1402

0 نظر

اندیکاتور «ایچیموکو» (Ichimoku) یک ابزار بسیار قدرتمند برای پیش‌بینی و توجیه رفتار قیمت است که علاوه بر دقت و توانایی بالا، پرکاربرد نیز هست. در این مطلب، با پیاده سازی اندیکاتور ایچیموکو در پایتون آشنا می‌شویم.

فهرست مطالب این نوشته

آشنایی با اندیکاتور ایچیموکو

فراخوانی مجموعه داده در پایتون

پیاده‌سازی اندیکاتور ایچیموکو در پایتون

مصورسازی نمودار اندیکاتور ایچیموکو

طراحی ویژگی‌ها برای محاسبه سیگنال

رسم نمودار سیگنال‌ها

جمع‌بندی

آشنایی با اندیکاتور ایچیموکو

این اندیکاتور شامل ۵ جزء اصلی است:

«تنکان سن» (Tenkan-sen): این جزء یک میانگین متحرک از بیشترین و کمترین قیمت مشاهده شده در 9 دوره گذشته است.
«کیجون سن» (Kijun-sen): این جزء یک میانگین متحرک از بیشترین و کمترین قیمت مشاهده شده در 26 دوره گذشته است.
«چیکو اسپن» (Chikou span): این جزء همان مقدار Close است که در 26 دوره گذشته رسم شده است.
«سنکو اسپن» A (Sekou span A): این جزء میانگین تنکان سن و کیجون سن را در 26 دوره بعد رسم می‌کند.
«سنکو اسپن» B (Senkou span B): این جزء یک میانگین متحرک از بیشترین و کمترین قیمت مشاهده شده در 52 دوره گذشته است که در 26 دوره بعد رسم می‌شود.

جزء دیگری نیز به نام «ابر کومو» (Kumo Cloud) وجود دارد که ناحیه بین سنکو اسپن A و سنکو اسپن B است.

فیلم آموزش تحلیل تکنیکال با ایچیموکو Ichimoku برای سرمایه گذاری – مقدماتی در تم آف

کلیک کنید

فراخوانی مجموعه داده در پایتون

ابتدا کتابخانه‌های مورد نیاز را فراخوانی می‌کنیم:

import numpy as np
import pandas as pd
import pandas_datareader as pdt
import matplotlib.pyplot as plt

این کتابخانه‌ها به ترتیب برای موارد زیر استفاده خواهند شد:

کار با آرایه (Array) و محاسبات برداری
کار با دیتافریم (Dataframe) و محاسبات مربوط به اندیکاتور
دریافت مجموعه داده (Dataset) مربوط به قیمت نمادها به صورت آنلاین (Online)
رسم نمودار قیمت و اندیکاتور (Indicator)

تنظیمات زیر را برای نمودارها اعمال می‌کنیم:

plt.style.use('ggplot')

حال مجموعه داده روزانه مربوط به رمزارز (Cryptocurrency) بیتکوین (Bitcoin) را به شکل یک دیتافریم دریافت می‌کنیم:

DF = pdt.DataReader('BTC-USD',
                    data_source='yahoo',
                    start='2020-01-01',
                    end='2022-01-01')

به این ترتیب، مجوعه داده دریافت می‌شود. برای مشاهده 10 سطر اول مجموعه داده به شکل زیر عمل می‌کنیم:

print(DF.head(10))

و خواهیم داشت:

                   High          Low         Open        Close       Volume    Adj Close
Date
2020-01-01  7254.330566  7174.944336  7194.892090  7200.174316  18565664997  7200.174316
2020-01-02  7212.155273  6935.270020  7202.551270  6985.470215  20802083465  6985.470215
2020-01-03  7413.715332  6914.996094  6984.428711  7344.884277  28111481032  7344.884277
2020-01-04  7427.385742  7309.514160  7345.375488  7410.656738  18444271275  7410.656738
2020-01-05  7544.497070  7400.535645  7410.451660  7411.317383  19725074095  7411.317383
2020-01-06  7781.867188  7409.292969  7410.452148  7769.219238  23276261598  7769.219238
2020-01-07  8178.215820  7768.227539  7768.682129  8163.692383  28767291327  8163.692383
2020-01-08  8396.738281  7956.774414  8161.935547  8079.862793  31672559265  8079.862793
2020-01-09  8082.295898  7842.403809  8082.295898  7879.071289  24045990466  7879.071289
2020-01-10  8166.554199  7726.774902  7878.307617  8166.554199  28714583844  8166.554199

حال برای نمایش مجموعه داده می‌توانیم به شکل زیر عمل کنیم:

plt.plot(DF['Close'], ls='-', lw=1, c='k', label='Close')
plt.title('Bitcoin Price')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.yscale('log')
plt.legend()
plt.show()

توجه داشته باشید که تعیین yscale به شکل log باعث می‌شود که مقیاس محور عمودی به شکل لگاریتمی (Logarithm) باشد.

پس از اجرا، شکل زیر را خواهیم داشت.

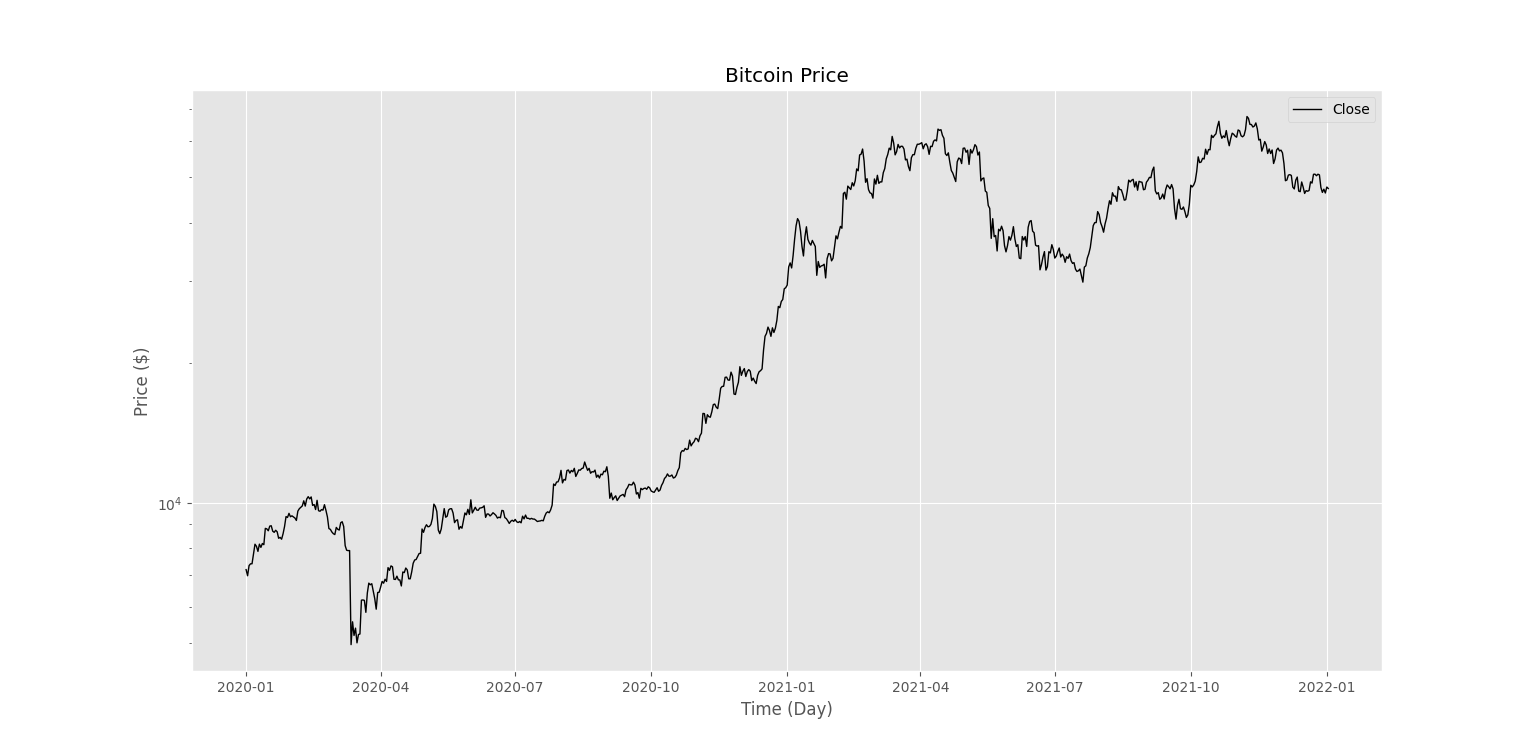
به این ترتیب، نمودار قیمت حاصل می‌شود.

فیلم آموزش تجزیه و تحلیل داده های مالی با پایتون – بخش یکم در تم آف

کلیک کنید

پیاده‌سازی اندیکاتور ایچیموکو در پایتون

برای پیاده‌سازی ایچیموکو، یک تابع ایجاد می‌کنیم که در ورودی، دیتافریم داده، طول پنجره تنکان سن، طول پنجره کیجون سن، طول جابه‌جایی (Displacement) و طول پنجره سنکو اسپن B را دریافت می‌کند:

def Ichimoku(DF:pd.core.frame.DataFrame, Lt:int=9, Lk:int=26, Ld:int=26, La:int=52):

حال برای محاسبه تنکان سن، یک ستون با این اسم تعریف و میانگین گفته‌شده را با استفاده از متدهای (Method) rolling, min, max اعمال می‌کنیم:

def Ichimoku(DF:pd.core.frame.DataFrame, Lt:int=9, Lk:int=26, Ld:int=26, La:int=52):
    DF['Tenkan-sen'] = (DF['High'].rolling(Lt).max() + DF['Low'].rolling(Lt).min()) / 2

حال مشابه کد فوق را برای کیجون سن نیز تکرار می‌کنیم:

def Ichimoku(DF:pd.core.frame.DataFrame, Lt:int=9, Lk:int=26, Ld:int=26, La:int=52):
    DF['Tenkan-sen'] = (DF['High'].rolling(Lt).max() + DF['Low'].rolling(Lt).min()) / 2
    DF['Kijun-sen'] = (DF['High'].rolling(Lk).max() + DF['Low'].rolling(Lk).min()) / 2

حال، نیاز است چیکو اسپن را پیاده‌سازی کنیم. برای این جزء تنها استفاده از متد shift کافی خواهد بود:

def Ichimoku(DF:pd.core.frame.DataFrame, Lt:int=9, Lk:int=26, Ld:int=26, La:int=52):
    DF['Tenkan-sen'] = (DF['High'].rolling(Lt).max() + DF['Low'].rolling(Lt).min()) / 2
    DF['Kijun-sen'] = (DF['High'].rolling(Lk).max() + DF['Low'].rolling(Lk).min()) / 2
    DF['Chikou span'] = DF['Close'].shift(-Ld)

برای پیاده‌سازی سنکو اسپن A تنها از عملگر جمع و تقسیم ستون‌ها استفاده می‌کنیم. سپس با متد shift این ستون را در زمان به جلو جابه‌جا می‌کنیم:

def Ichimoku(DF:pd.core.frame.DataFrame, Lt:int=9, Lk:int=26, Ld:int=26, La:int=52):
    DF['Tenkan-sen'] = (DF['High'].rolling(Lt).max() + DF['Low'].rolling(Lt).min()) / 2
    DF['Kijun-sen'] = (DF['High'].rolling(Lk).max() + DF['Low'].rolling(Lk).min()) / 2
    DF['Chikou span'] = DF['Close'].shift(-Ld)
    DF['Senkou span A'] = ((DF['Tenkan-sen'] + DF['Kijun-sen']) / 2).shift(Ld)

برای پیاده‌سازی سنکو اسپن B نیز همانند تنکان سن و کیجون سن عمل می‌کنیم، با این تفاوت که از shift نیز استفاده می‌کنیم:

def Ichimoku(DF:pd.core.frame.DataFrame, Lt:int=9, Lk:int=26, Ld:int=26, La:int=52):
    DF['Tenkan-sen'] = (DF['High'].rolling(Lt).max() + DF['Low'].rolling(Lt).min()) / 2
    DF['Kijun-sen'] = (DF['High'].rolling(Lk).max() + DF['Low'].rolling(Lk).min()) / 2
    DF['Chikou span'] = DF['Close'].shift(-Ld)
    DF['Senkou span A'] = ((DF['Tenkan-sen'] + DF['Kijun-sen']) / 2).shift(Ld)
    DF['Senkou span B'] = ((DF['High'].rolling(La).max() + DF['Low'].rolling(La).min()) / 2).shift(Ld)

به این ترتیب، هر پنج جزء جداگانه محاسبه و به دیتافریم اضافه می‌کنیم. در انتهای تابع، نیازی به برگرداندن دیتافریم نیست، زیرا تغییرات بر روی دیتافریم اصلی اعمال شده است و از این طریق قابل دسترسی است.

برای استفاده از تابع پیاده‌سازی شده، به شکل زیر عمل می‌کنیم:

Ichimoku(DF)

به این ترتیب، هر پنج جزء اندیکاتور ایچیموکو با تنظیمات پیش‌فرض به دیتافریم افزوده می‌شود.

مصورسازی نمودار اندیکاتور ایچیموکو

حال می‌توانیم یک نمودار برای قیمت و اندیکاتور در کنار هم رسم کنیم:

plt.plot(DF['Close'], ls='-', lw=1, c='k', label='Close')
plt.plot(DF['Tenkan-sen'], ls='-', lw=0.8, c='r', label='Tenkan-sen')
plt.plot(DF['Kijun-sen'], ls='-', lw=0.8, c='b', label='Kijun-sen')
plt.plot(DF['Chikou span'], ls='--', lw=0.8, c='g', label='Chikou span')
plt.plot(DF['Senkou span A'], ls='--', lw=0.8, c='g', label='Senkou span A')
plt.plot(DF['Senkou span B'], ls='--', lw=0.8, c='r', label='Senkou span B')
plt.fill_between(DF.index, DF['Senkou span A'], DF['Senkou span B'], where=(DF['Senkou span A'] > DF['Senkou span B']), color='lime', alpha=0.7)
plt.fill_between(DF.index, DF['Senkou span A'], DF['Senkou span B'], where=(DF['Senkou span A']

پس از اجرا کد، نمودار زیر حاصل می‌شود.

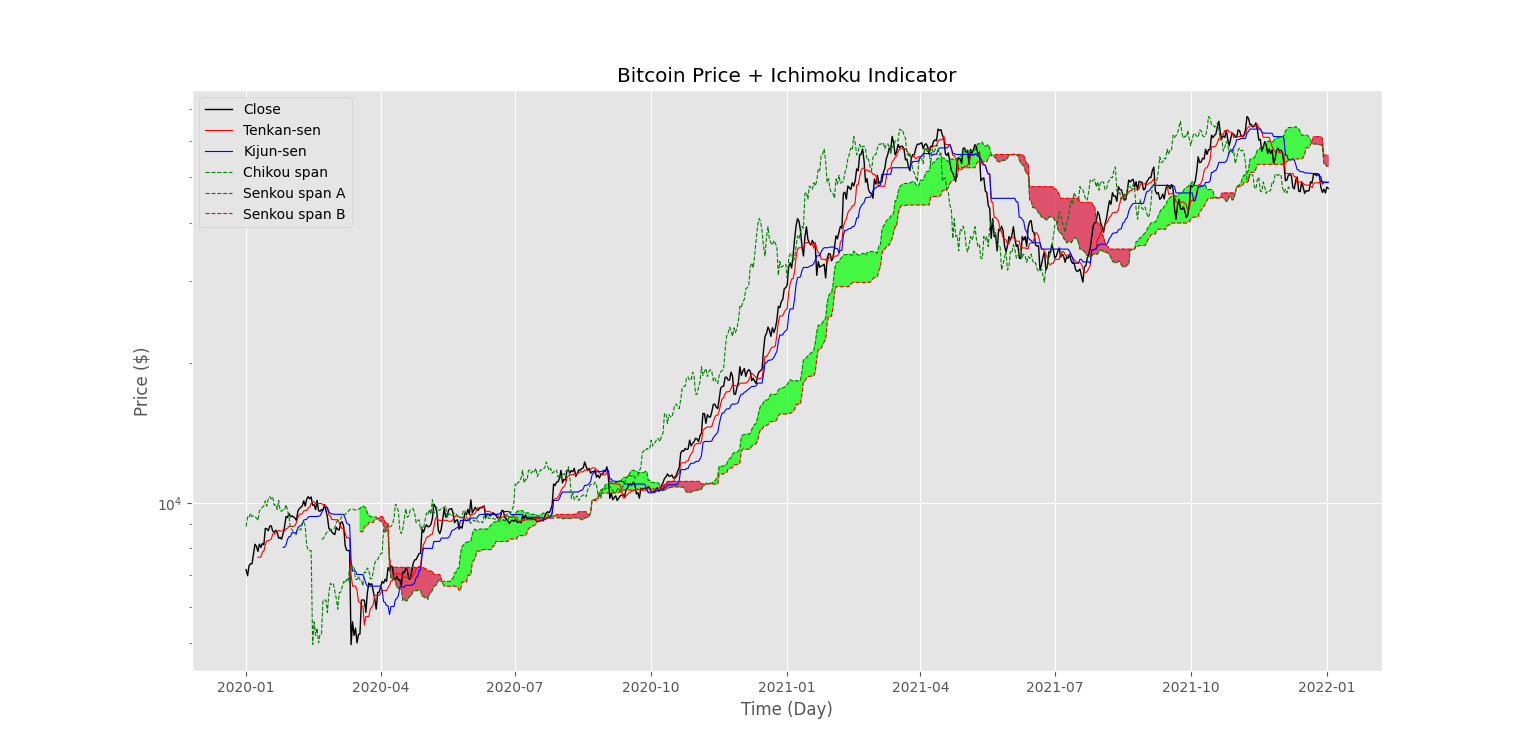
به این ترتیب، مشاهده می‌کنیم که اندیکاتور به خوبی رفتار مورد انتظار را از خود نشان می‌دهد.

فیلم آموزش تحلیل تکنیکال با ایچیموکو Ichimoku برای سرمایه گذاری- تکمیلی در تم آف

کلیک کنید

طراحی ویژگی‌ها برای محاسبه سیگنال

از اجزای مختلف این اندیکاتور می‌توان سیگنال‌های مختلفی گرفت. برای مثال:

موقعیت قیمت نسبت به تنکان سن
موقعیت قیمت نسبت به کیجون سن
موقعیت تنکان سن نسبت به کیجون سن
رنگ و ضخامت ابر کومو (موقعیت سنکو اسپن A نسبت به سنکو اسپن B)
موقعیت قیمت دوره فعلی نسبت به قیمت 26 دوره گذشته
موقعیت قیمت نسبت به سنکو اسپن A
موقعیت قیمت نسبت به سنکو اسپن B

توجه داشته باشید که به جز هفت مورد اشاره شده، ویژگی‌های زیاد دیگری نیز می‌توانند محاسبه شوند. در این مطلب تنها به این هفت مورد بسنده خواهیم کرد.

فیلم آموزش کاربرد پایتون در بازارهای مالی – دریافت و پردازش قیمت رمزارزها (رایگان) در تم آف

کلیک کنید

توجه داشته باشید که برای محاسبه موقعیت نسبی یک ویژگی نسبت به دیگری، روش‌های مختلفی وجود دارد که در این مطلب قصد داریم از لگاریتم نسبت استفاده کنیم. برای محاسبه این مقدار بین ویژگی $$S_1$$ و $$S_2$$ به شکل زیر عمل می‌کنیم:

$$ L R_{t}=log left(frac{S_{1 t}}{S_{2 t}}right) $$

به این ترتیب، این 7 معیار می‌توانند پرکاربرد باشند. برای محاسبه این سیگنال‌ها، می‌توان تابعی جدید ایجاد کرد که با گرفتن دیتافریم شامل مقادیر اندیکاتور، این 7 سیگنال را محاسبه کند. با توجه به اینکه محاسبه موقعیت نسبی برای هر 7 معیار نیاز است، می‌توانیم آن را به شکلی جداگانه در قالب یک تابع ایجاد کنیم. این تابع در ورودی دو ستون را گرفته و در خروجی لگاریتم نسبت آن دو را برمی‌گرداند:

def LR(S1:pd.core.frame.Series, S2:pd.core.frame.Series):
    lr = np.log(S1 / S2)
    return lr

حال می‌توانیم تابع مربوط به سیگنال ایچیموکو را پیاده‌سازی کنیم. این تابع در ورودی دیتافریم نهایی حاصل از مرحله قبل و طول جابه‌جایی را دریافت می‌کند و تغییرات مورد نیاز را بر روی آن اعمال می‌کند:

def Ichimoku2(DF:pd.core.frame.DataFrame, Ld:int=26):

توجه داشته باشید که می‌توانیم به جای قیمت Close از قیمت HLC که به شکل زیر محاسبه می‌شود استفاده کنیم:

$$ H L C_{t}=frac{H i g h_{t}+L o w_{t}+ { Close }_{t}}{3} $$

برای محاسبه این ستون خواهیم داشت:

def Ichimoku2(DF:pd.core.frame.DataFrame, Ld:int=26):
    DF['HLC'] = (DF['High'] + DF['Low'] + DF['Close']) / 3

حال، می‌توانیم اولین ویژگی را بین ستون HLC و ستون Tenkan-sen محاسبه و اضافه کنیم:

def Ichimoku2(DF:pd.core.frame.DataFrame, Ld:int=26):
    DF['HLC'] = (DF['High'] + DF['Low'] + DF['Close']) / 3
    DF['LR(HLC, Tenkan-sen)'] = LR(DF['HLC'], DF['Tenkan-sen'])

به این ترتیب، برای ویژگی‌های دوم، سوم و چهارم نیز خواهیم داشت:

def Ichimoku2(DF:pd.core.frame.DataFrame, Ld:int=26):
    DF['HLC'] = (DF['High'] + DF['Low'] + DF['Close']) / 3
    DF['LR(HLC, Tenkan-sen)'] = LR(DF['HLC'], DF['Tenkan-sen'])
    DF['LR(HLC, Kijun-sen)'] = LR(DF['HLC'], DF['Kijun-sen'])
    DF['LR(Tenkan-sen, Kijun-sen)'] = LR(DF['Tenkan-sen'], DF['Kijun-sen'])
    DF['LR(Senkou span A, Senkou span B)'] = LR(DF['Senkou span A'], DF['Senkou span B'])

به این ترتیب، چهار ویژگی اول محاسبه می‌شود. برای محاسبه ویژگی پنجم به شکل زیر عمل می‌کنیم:

def Ichimoku2(DF:pd.core.frame.DataFrame, Ld:int=26):
    DF['HLC'] = (DF['High'] + DF['Low'] + DF['Close']) / 3
    DF['LR(HLC, Tenkan-sen)'] = LR(DF['HLC'], DF['Tenkan-sen'])
    DF['LR(HLC, Kijun-sen)'] = LR(DF['HLC'], DF['Kijun-sen'])
    DF['LR(Tenkan-sen, Kijun-sen)'] = LR(DF['Tenkan-sen'], DF['Kijun-sen'])
    DF['LR(Senkou span A, Senkou span B)'] = LR(DF['Senkou span A'], DF['Senkou span B'])
    DF['LR(HLC, HLC)'] = LR(DF['HLC'], DF['HLC'].shift(Ld))

حال، برای محاسبه ویژگی‌های ششم و هفتم خواهیم داشت:

def Ichimoku2(DF:pd.core.frame.DataFrame, Ld:int=26):
    DF['HLC'] = (DF['High'] + DF['Low'] + DF['Close']) / 3
    DF['LR(HLC, Tenkan-sen)'] = LR(DF['HLC'], DF['Tenkan-sen'])
    DF['LR(HLC, Kijun-sen)'] = LR(DF['HLC'], DF['Kijun-sen'])
    DF['LR(Tenkan-sen, Kijun-sen)'] = LR(DF['Tenkan-sen'], DF['Kijun-sen'])
    DF['LR(Senkou span A, Senkou span B)'] = LR(DF['Senkou span A'], DF['Senkou span B'])
    DF['LR(HLC, HLC)'] = LR(DF['HLC'], DF['HLC'].shift(Ld))
    DF['LR(HLC, Senkou span A)'] = LR(DF['HLC'], DF['Senkou span A'])
    DF['LR(HLC, Senkou span B)'] = LR(DF['HLC'], DF['Senkou span B'])

به این ترتیب، هر هفت ویژگی محاسبه شدند.

حال تابع ایجاد شده را اعمال می‌کنیم:

Ichimoku2(DF)

توجه داشته باشید که DF نهایی حاصل از این کد، مراحل زیر را طی کرده است:

DF = pdt.DataReader('BTC-USD',
                    data_source='yahoo',
                    start='2020-01-01',
                    end='2022-01-01')

Ichimoku(DF)

Ichimoku2(DF)

رسم نمودار سیگنال‌ها

حال برای رسم نمودار اولین ویژگی در کنار نمودار قیمت و تنکان سن، می‌توانیم به شکل زیر عمل کنیم:

plt.subplot(3, 1, (1, 2))
plt.plot(DF['Close'], ls='-', lw=0.8, c='k', label='Close')
plt.plot(DF['Tenkan-sen'], ls='-', lw=0.8, c='r', label='Tenkan-sen')
plt.title('Bitcoin Price')
plt.ylabel('Price ($)')
plt.yscale('log')
plt.xlim(left=DF.index[0], right=DF.index[-1])
plt.legend()
plt.tight_layout()

plt.subplot(3, 1, 3)
m=DF['LR(HLC, Tenkan-sen)'].abs().max()
plt.plot(DF['LR(HLC, Tenkan-sen)'], ls='-', lw=0.7, c='k')
plt.fill_between(DF.index, DF['LR(HLC, Tenkan-sen)'], np.zeros(len(DF['LR(HLC, Tenkan-sen)'])), where=(DF['LR(HLC, Tenkan-sen)']>0), color='lime', alpha=0.7)
plt.fill_between(DF.index, DF['LR(HLC, Tenkan-sen)'], np.zeros(len(DF['LR(HLC, Tenkan-sen)'])), where=(DF['LR(HLC, Tenkan-sen)']

به این ترتیب، دو سوم صفحه به نمودار «نیمه-لگاریتمی» (Semi-Logarithm) قیمت و تنکان سن تخصیص داده می‌شود و لگاریتم نسبت HLC به تنکان سن در زیر آن رسم می‌شود. با توجه به اینکه برای تمامی روزها، نسبت گفته شده قابل محاسبه نیست، باید محور x هر دو نمودار بین تاریخ شروع مجموع داده و تاریخ اتمام آن ثابت شود که به این منظور از plt.xlim استفاده می‌کنیم. مقادیر تاریخ داده‌های نیز از طریق DF.index قابل دسترس است که عضو اول و آخری مربوط به روزهای شروع و اتمام مجموعه داده است.

فیلم آموزش برنامه نویسی پایتون Python – مقدماتی در تم آف

کلیک کنید

توجه داشته باشید که ویژگی حاصل با این‌که رفتار قرینه دارد، ولی ممکن است در یک بازه مشخص، مقادیر مثبت یا منفی بیشتری به خود گرفته باشد که این اتفاق باعث می‌شود تا خط صفر (Zero Line) در وسط فریم نمودار قرار نگیرد. به همین دلیل از بیشترین مقدار قدرمطلق نسبت، برای محدود کردن محور y نیز استفاده می‌کنیم که با استفاده از plt.ylim قابل انجام است.

پس از اجرای کد، شکل زیر را خواهیم داشت.

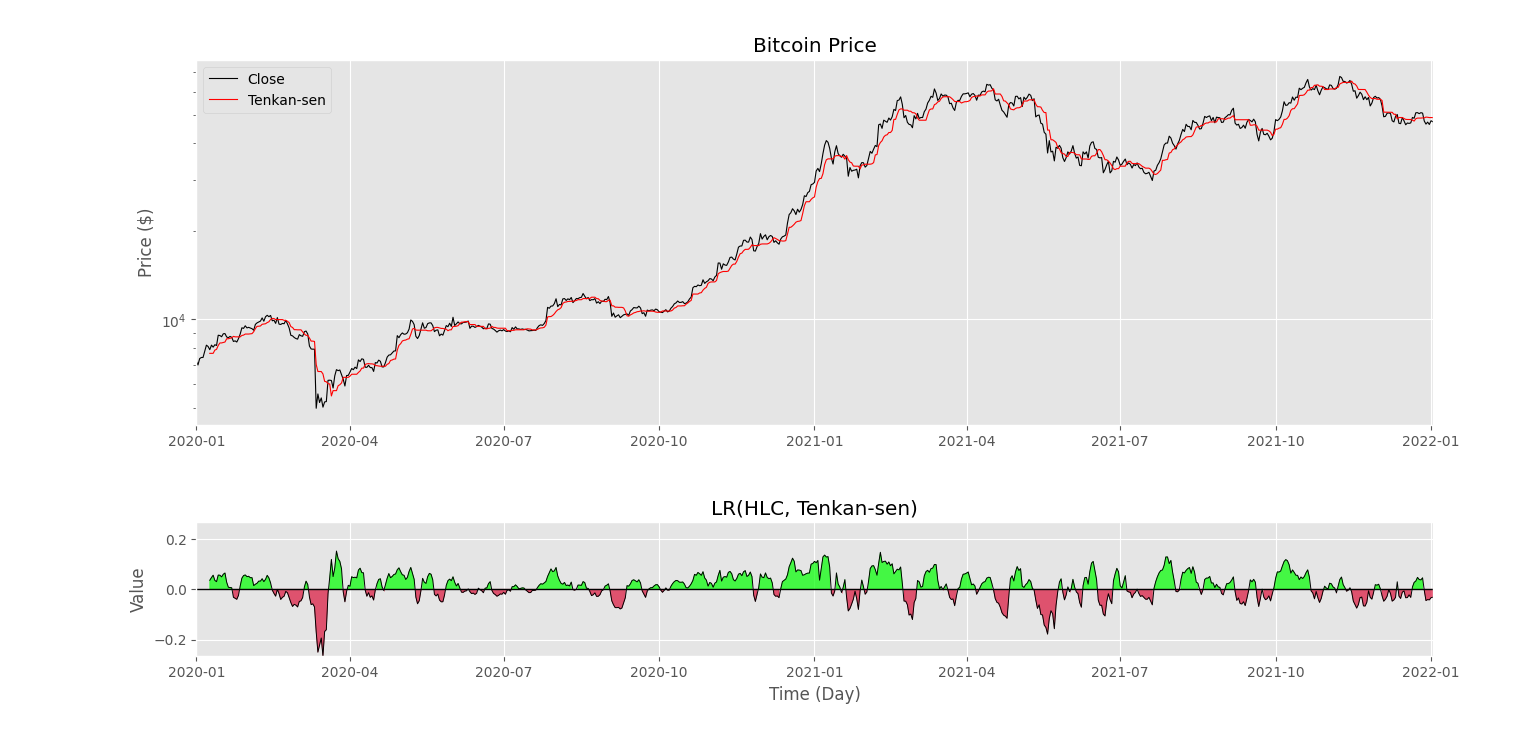
به این ترتیب، تطابق رنگ و مقدار سیگنال با موقعیت قیمت با تنکان سن کاملاً مشهود است. نکته مهمی که باید به آن توجه کرد، محاسبه این نسبت با استفاده از HLC است، در حالی که روی نمودار از قیمت Close استفاده شده است. به این دلیل، امکان مشاهده برخی اختلاف‌های ریز وجود دارد. نکته مهمی که وجود دارد، ادامه‌دار بودن روند صعودی در زمان تشکیل سیگنال سبز است.

اگر نمودار فوق را برای کیجون سن تکرار کنیم، شکل زیر را خواهیم داشت.

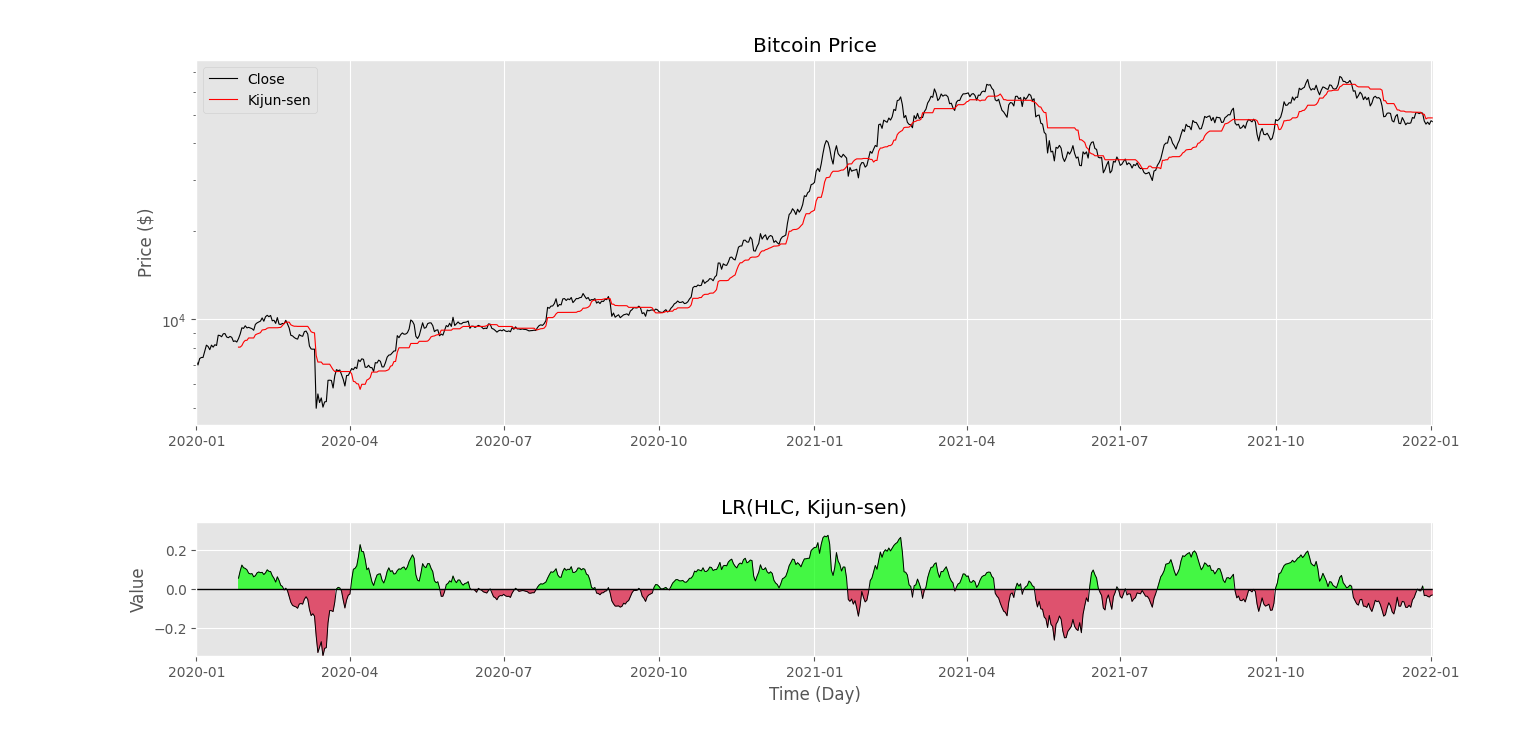
به این ترتیب، مشاهده می‌کنیم که رفتار در مورد کیجون سن، متعادل‌تر است که به دلیل بزرگ‌تر بودن بازه محاسبه آن است. نکته مهم دیگری که وجود دارد، همرنگی سیگنال با روند است، با این تفاوت که روندهای بلند مدت‌تر در این سیگنال قابل محاسبه هستند.

تا به اینجا 7 ویژگی مختلف محاسبه شد که هرکدام از جهتی سعی در نشان دادن وضعیت بازار دارند. برای ساخت یک سیستم معاملاتی خوب، نیاز داریم که همگی این موارد را در محاسبات دخیل کنیم که برای این کار روش‌های فراوانی وجود دارد. یکی از ساده‌ترین روش‌ها، میانگین‌گیری از سیگنال‌ها است و تنها به شرطی قابل انجام است که رنگ سبز سیگنال‌ها به معنی حرکات مثبت و صعودی باشد. با توجه به اینکه در مورد هر هفت سیگنال محاسبه‌شده این ویژگی صادق است، می‌توانیم میانگین آن‌ها را به عنوان سیگنال نهایی استفاده کنیم. به این منظور تابع Ichimoku2 را به شکل زیر تغییر می‌دهیم:

def Ichimoku2(DF:pd.core.frame.DataFrame, Ld:int=26):
    DF['HLC'] = (DF['High'] + DF['Low'] + DF['Close']) / 3
    DF['LR(HLC, Tenkan-sen)'] = LR(DF['HLC'], DF['Tenkan-sen'])
    DF['LR(HLC, Kijun-sen)'] = LR(DF['HLC'], DF['Kijun-sen'])
    DF['LR(Tenkan-sen, Kijun-sen)'] = LR(DF['Tenkan-sen'], DF['Kijun-sen'])
    DF['LR(Senkou span A, Senkou span B)'] = LR(DF['Senkou span A'], DF['Senkou span B'])
    DF['LR(HLC, HLC)'] = LR(DF['HLC'], DF['HLC'].shift(Ld))
    DF['LR(HLC, Senkou span A)'] = LR(DF['HLC'], DF['Senkou span A'])
    DF['LR(HLC, Senkou span B)'] = LR(DF['HLC'], DF['Senkou span B'])
    DF['TS'] = DF.iloc[:, -7:].mean(axis=1)

توجه داشته باشید که به دلیل طولانی شدن عبارات در صورت جمع زدن دستی ستون‌ها، از این فرمت استفاده کردیم. نکته دیگری که باید به ان توجه کرد، اضافه شدن ستون‌های جدید به انتهای دیتافریم است. به همین دلیل، هفت ستون آخر، مربوط به هفت سیگنال اضافه‌شده هستند.

اگر برای سیگنال نهایی نمودار را رسم کنیم، شکل زیر را خواهیم داشت.

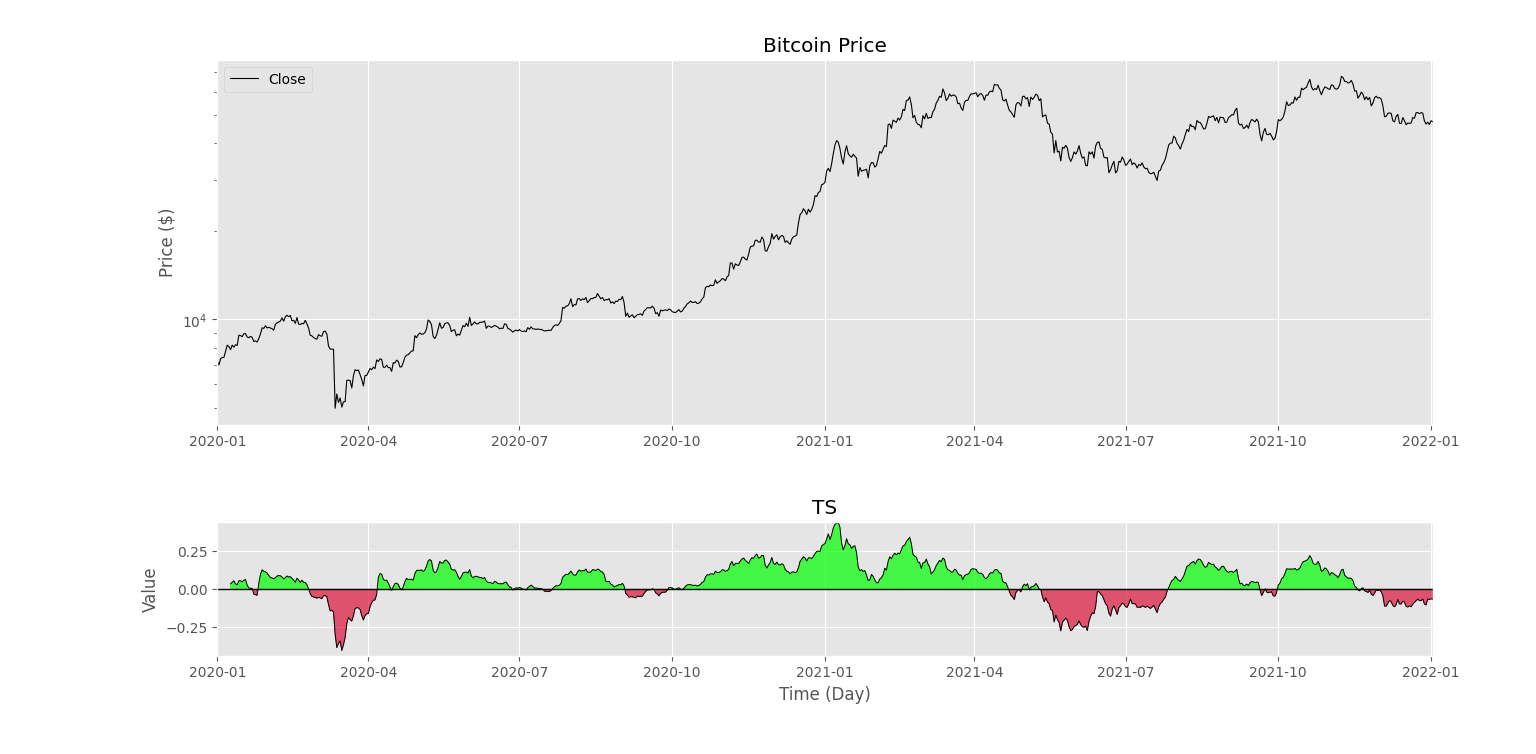
به این ترتیب، مشاهده می‌کنیم که میانگین هفت سیگنال، رفتار دقیق‌تری داشته و نسبت به روندهای کوتاه‌مدت واکنش کمتری داده است.

فیلم آموزش پیاده سازی اندیکاتورهای تکنیکال با پایتون Python – بخش یکم در تم آف

کلیک کنید

جمع‌بندی

در این مطلب با اندیکاتور ایچیموکو آشنا و آن را پیاده‌سازی کردیم. سپس روش استفاده معامله‌گران از این اندیکاتور را در قالب سیگنال‌هایی محاسبه کردیم و در قالب نمودارهایی آن‌ها را با نمودار قیمت تطبیق دادیم.

برای مطالعه بیشتر می‌توان موارد زیر را بررسی کرد:

چرا میانگین بیشترین و کمترین قیمت مشاهده شده در L دوره گذشته دارای اهمیت است؟
به جز موارد گفته شده، چه سیگنال‌های دیگری می‌توان از این اندیکاتور گرفت؟
چگونه می‌توان یک ربات معامله‌گر بر پایه اندیکاتور ایچیموکو ایجاد کرد؟
نمودار مربوط به 5 سیگنال دیگر را رسم و دقت هرکدام را بررسی کنید. هرکدام چه ویژگی‌هایی دارند؟
اگر به جای لگاریتم نسبت مقادیر، از تفاضل مقادیر استفاده می‌کردیم، چه مشکلاتی رخ می‌داد؟
اگر برای محاسبه این اندیکاتور، به جای کتابخانه Pandas از کتابخانه Numpy استفاده می‌کردیم، چه مشکلاتی ممکن بود رخ دهد؟
یکی از ویژگی‌های مهم سنکو اسپن B مسطح شدن (Flatten) آن است که اغلب قیمت واکنش بسیار خوبی به این مناطق می‌دهد. چگونه می‌توان این نواحی را شناسایی و استفاده کرد؟

آموزش وردپرس

آشنایی با اندیکاتور ایچیموکو

فراخوانی مجموعه داده در پایتون

پیاده‌سازی اندیکاتور ایچیموکو در پایتون

مصورسازی نمودار اندیکاتور ایچیموکو

طراحی ویژگی‌ها برای محاسبه سیگنال

رسم نمودار سیگنال‌ها

جمع‌بندی

دیدگاهتان را بنویسید لغو پاسخ