شبیه سازی پیاده روی تصادفی در پایتون — راهنمای گام به گام

پیاده روی تصادفی (Random Walk) فرایندی است که در طول زمان رخ می‌دهد و هر قدم (Step) به‌صورت تصادفی ایجاد می‌شود و موقعیت بعدی را ایجاد می‌کند. در این آموزش، با روش شبیه سازی پیاده روی تصادفی در پایتون آشنا می‌شویم.

پیاده روی تصادفی چیست؟

در شکل زیر حرکت براونی (Brownian Motion) برای ذرات گاز نشان داده شده است که نقطه ابتدا و انتها نشان داده شده و نمونه‌ای از پیاده روی تصادفی است.

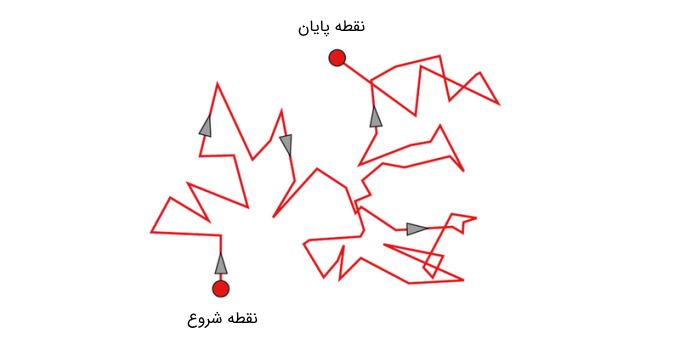
در پیاده‌روی تصادفی، از توزیع‌های مختلف مانند یکنواخت و نرمال می‌توان استفاده کرد. اندازه گام نیز می‌تواند پیوسته یا گسسته باشد.

ابتدا می‌خواهیم یک پیاده‌روی تصادفی در دو بعد ایجاد کنیم. بدین منظور، یک موقعیت برای ذره تعریف می‌کنیم:

$$ begin{aligned}
&x_{0}=0 \
&y_{0}=0
end{aligned} $$

سپس به تعداد مراحلی مشخص (N) اعدادی تصادفی با توزیع یکنواخت از $$-1$$ تا $$+1$$ ایجاد می‌کنیم:

$$begin{aligned}
&Delta x_{t}=text { uniform }(-1,+1) \
&Delta y_{t}=text { uniform }(-1,+1)
end{aligned}$$

سپس، می‌توانیم موقعیت ذره را اصلاح کنیم:

$$begin{aligned}
&x_{t}=x_{t-1}+Delta x_{t} \
&y_{t}=y_{t-1}+Delta y_{t}
end{aligned}$$

به این ترتیب، موقعیت در هر لحظه، از روی موقعیت قبلی و با تغییراتی تصادفی ایجاد می‌شود.

فیلم آموزش پیاده سازی اندیکاتورهای تکنیکال با پایتون Python – بخش یکم در تم آف

کلیک کنید

پیاده روی تصادفی در پایتون

برای پیاده‌سازی، وارد محیط برنامه‌نویسی می‌شویم:

import numpy as np
import matplotlib.pyplot as plt

حال تنظیمات زیر را اعمال می‌کنیم:

np.random.seed(0)
plt.style.use('ggplot')

در ابتدا، موقعیت‌های اولیه را تعریف می‌کنیم:

x0 = 0
y0 = 0

سپس تعداد گام‌های شبیه‌سازی را تعریف می‌کنیم:

N = 100

حال یک فهرست برای ذخیره Xها و یک فهرست دیگر برای ذخیره Yها ایجاد می‌کنیم:

X = [x0]
Y = [y0]

حال می‌توانیم یک حلقه ایجاد می‌کنیم و در هر مرحله، به‌صورت تصادفی اندازه گام محاسبه و به آخرین موقعیت اضافه کنیم:

for _ in range(N):
    dx = np.random.uniform(low=-1, high=+1)
    dy = np.random.uniform(low=-1, high=+1)
    newx = X[-1] + dx
    newy = Y[-1] + dy
    X.append(newx)
    Y.append(newy)

به این ترتیب، مقادیر محاسبه و در دو فهرست ذخیره می‌شود. حال می‌توانیم یک نموداری براساس دو لیست ایجاد کنیم تا حرکات به‌خوبی مشاهده شود:

plt.plot(X, Y, ls='--', lw=0.9, c='crimson', marker='o', ms=4)
plt.title('Random Walk')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

به این ترتیب، نمودار زیر مشاهده می‌شود.

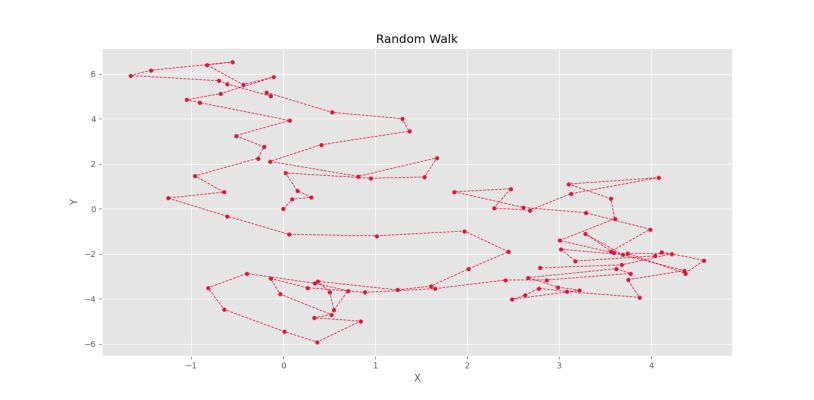
به این ترتیب، حرکات به‌خوبی نشان داده می‌شود.

برای یادگیری برنامه‌نویسی با زبان پایتون، پیشنهاد می‌کنیم به مجموعه آموزش‌های مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه آموزش‌های برنامه نویسی پایتون (Python) — مقدماتی تا پیشرفته + اینجا کلیک کنید.

می‌توانیم برنامه را به‌شکل زیر اصلاح کنیم و به‌شکل برداری بنویسیم:

P = np.zeros((N+1, 2))

for i in range(N):
    P[i+1] = P[i] + np.random.uniform(low=-1, high=+1, size=(2, ))

plt.plot(P[:, 0], P[:, 1], ls='--', lw=0.9, c='crimson', marker='o', ms=4)
plt.title('Random Walk')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

در این حالت نیز نتایج قبلی ایجاد خواهد شد. می‌توان گام‌ها را به‌صورت تصادفی با توزیع نرمال ایجاد کرد:

for i in range(N):
    P[i+1] = P[i] + np.random.normal(loc=0, scale=1, size=(2, ))

که در این صورت، نموداری به شکل زیر خواهد بود.

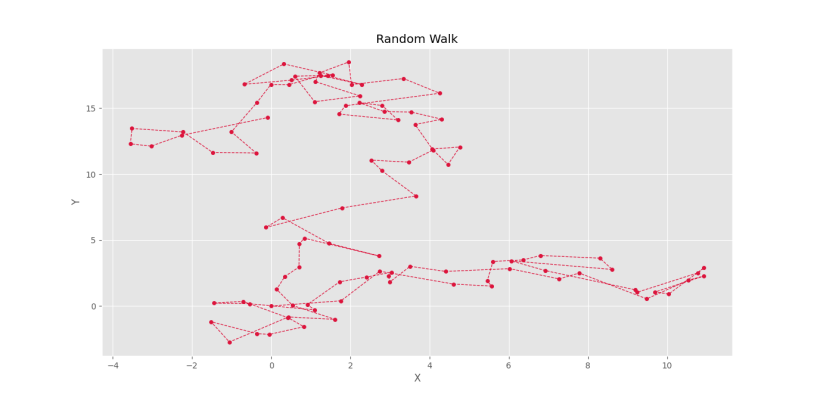
توجه داشته باشید که با توجه به رفتار هر سیستم، باید از توزیع متناسبی استفاده کرد.

به این ترتیب، شبیه‌سازی پیاده‌روی تصادفی دوبعدی پیاده‌سازی شد.

حال می‌خواهیم در بخش دوم از مطلب، به شبیه‌سازی پیاده‌روی تصادفی قیمت یک نماد بپردازیم. توجه داشته باشید که در این حالت، پیشفرضمان را به این صورت در نظر می‌گیریم که رفتار سری زمانی کاملاً تصادفی بوده و توزیع حرکات را می‌دانیم.

به این منظور، کتابخانه‌های مورد نیاز را فراخوانی می‌کنیم و تنظمات را اعمال می‌کنیم:

import numpy as np
import yfinance as yf
import matplotlib.pyplot as plt

np.random.seed(0)
plt.style.use('ggplot')

حال می‌توانیم داده‌های روزانه را برای سه سال دریافت کرده و تغییرات نسبی روزانه را محاسبه کنیم:

DF = yf.download('BTC-USD', start='2019-01-01', end='2022-01-01', interval='1d')
C = DF['Close'].to_numpy()
R = C[1:] / C[:-1] - 1

توجه داشته باشید که می‌توان به‌شکل زیر نیز عمل کرد:

DF = yf.download('BTC-USD', start='2019-01-01', end='2022-01-01', interval='1d')
C = DF['Close'].to_numpy()
R = DF['Close'].pct_change().dropna().to_numpy()

حال می‌توانیم یک نمودار هیستوگرام (Histogram Plot) برای تغییرات نسبی قیمت رسم کنیم:

plt.hist(R, bins=51, color='crimson', alpha=0.8)
plt.title('Relative Change Histogram')
plt.xlabel('Relative Change')
plt.ylabel('Frequency')
plt.show()

که شکل زیر را خواهیم داشت.

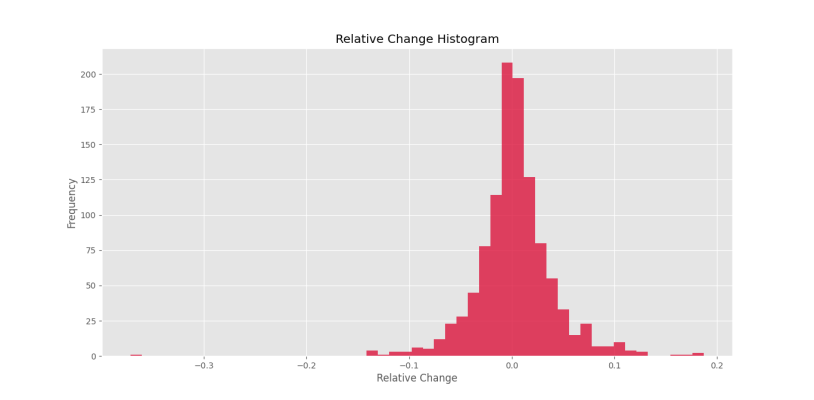
مشاهده می‌کنیم که توزیع داده‌ها به توزیع نرمال نزدیک است. به همین دلیل، می‌توانیم از توزیع نرمال برای تولید گام‌ها استفاده کنیم. برای ایجاد این توزیع، میانگین (Mean) و انحراف معیار (Standard Deviation) داده‌ها را محاسبه می‌کنیم:

m = np.mean(R)
s = np.std(R)

حال می‌توانیم موقعیت اولیه را تعریف کنیم:

p = C[-1]

حال تعداد گام را تعیین و یک آرایه برای ذخیره مقادیر جدید ایجاد می‌کنیم:

N = 200

P = np.zeros(N)

حال می‌توانیم حلقه اصلی را ایجاد کنیم و مقدایر گام را تعیین کنیم:

for i in range(N):
    r = np.random.normal(loc=m, scale=s)

عدد $$r$$ نشان‌دهنده تغییرات نسبی خواهد بود:

$$ r=frac{P_{t+1}}{P_{t}}-1 Rightarrow r+1=frac{P_{t+1}}{P_{t}} Rightarrow P_{t+1}=P_{t} times(r+1) $$

اکنون مقدار بعدی را می‌توانیم محاسبه کنیم:

for i in range(N):
    r = np.random.normal(loc=m, scale=s)
    p *= (r + 1)
    P[i] = p

به این ترتیب، مقادیر محاسبه شد. برای رسم نمودار، به شکل زیر عمل می‌کنیم:

plt.semilogy(T1, C, lw=0.8, c='crimson', label='Real Data')
plt.semilogy(T2, P, lw=0.8, c='teal', label='Random Walk')
plt.title('Real Data + Random Walk')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()

که در این صورت، نمودار به شکل زیر خواهد بود.

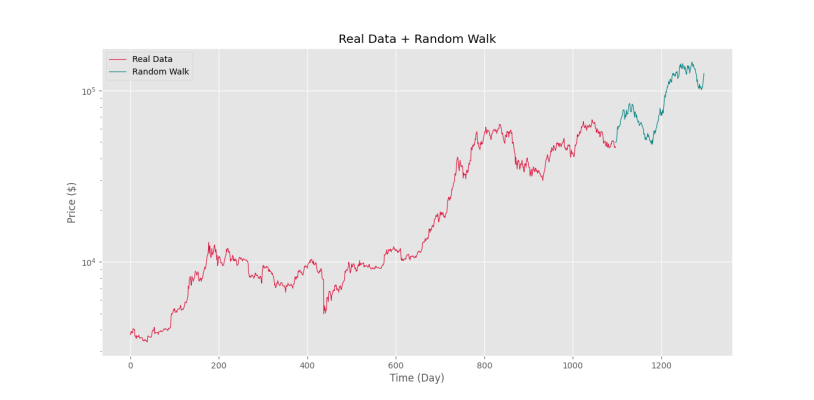
به این ترتیب، مشاهده می‌کنیم که اندازه و توزیع تغییرات، بسیار نزدیک به نمودار واقعی است. توجه داشته باشید که می‌توان ابتدا روند خطی را از داده‌‌ها حذف کرده و سپس پیاده‌روی تصادفی را شبیه‌سازی کنیم که در این صورت، داده‌های تولیدشده به واقعیت نزدیک خواهند بود. همچنین، می‌توان خودهمبستگی (Autocorrelation) تغییرات با روزهای گذشته خود را مدل و براساس آن حرکات تصادفی را ایجاد کرد.

اگر بخواهیم چندین سناریو را به‌صورت همزمان در نمودار نشان دهیم، می‌توانیم به شکل زیر کد را تغییر دهیم:

N = 200
nScenario = 10

T1 = np.arange(start=0, stop=C.size)
T2 = np.arange(start=C.size, stop=C.size + N)

plt.semilogy(T1, C, lw=0.8, c='crimson', label='Real Data')
for i in range(nScenario):
    p = C[-1]
    P = np.zeros(N)
    for i in range(N):
        r = np.random.normal(loc=m, scale=s)
        p *= (r + 1)
        P[i] = p
    plt.semilogy(T2, P, lw=0.6)
plt.title('Real Data + Random Walk')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()

که در این صورت، به تعداد ۱۰ بار، پیاده‌روی تصادفی انجام می‌شود و نتایج زیر حاصل می‌شود.

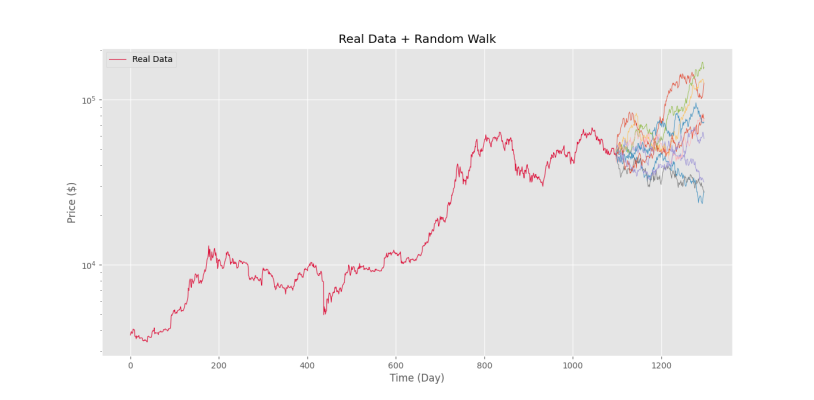
به این ترتیب، مشاهده می‌کنیم که هر سناریو از یک نقطه شروع شده ولی رفته‌رفته فاصله هرکدام از سایرین افزایش می‌یابد. با انجام یک مدل‌سازی مناسب و دقیق‌تر، می‌توان پیش‌بینی‌هایی انجام داد که به واقعیت نزدیک هستند و در نتیجه، با بررسی سناریو‌های مختلف، احتمال مشاهده قیمتی مشخص در تاریخی مشخص را محاسبه کرد.

جمع‌بندی

در این مطلب، با پیاده‌روی تصادفی آشنا شدیم و دو شبیه‌سازی با استفاده از آن انجام دادیم. برای مطالعه بیشتر، می‌توان به موارد زیر مراجعه کرد:

1. روند (Trend) در داده‌های سری زمانی
2. اجزای تشکیل‌دهنده یک سری زمانی
3. توزیع‌های احتمال پرکاربرد
4. خودهمبستگی در سری‌های زمانی