ساخت ربات معامله گر رمزارز با میانگین متحرک ساده در پایتون — بخش دوم

در بخش اول مطالب گذشته مجله تم آف به ساخت ربات معامله گر رمزارز با استفاده از استراتژی میانگین متحرک ساده در پایتون پرداختیم و آن را روی مجموعه داده آموزش (Train Dataset) ارزیابی کردیم. در این مطلب، قصد داریم با ایجاد تغییراتی در کدهای نوشته‌شده، قابلیت ارزیابی ربات معامله‌گر روی مجموعه داده آزمایش (Test Dataset) را نیز اضافه کنیم.

بهبود ربات معامله گر رمزارز

حال وارد محیط برنامه‌نویسی پایتون می‌شویم و کد نوشته شده مربوط به کلاس smaLR را وارد می‌کنیم:

import numpy as np
import pandas as pd
import pyswarm as ps
import pandas_datareader as pdt
import matplotlib.pyplot as plt

class smaLR:
    def __init__(self):
        self.TrainLog = []
    def GetData(self, Ticker:str, Start:str, End:str):
        self.Ticker = Ticker
        self.Start = Start
        self.End = End
        self.DF = pdt.DataReader(Ticker,
                                 data_source='yahoo',
                                 start=Start,
                                 end=End)
        self.DF.drop(labels=['High', 'Low', 'Volume', 'Adj Close'],
                     axis=1,
                     inplace=True)
    def ProcessData(self, L:int):
        self.L = L
        self.DF[f'SMA({L})'] = self.DF['Close'].rolling(L).mean()
        self.DF[f'Log-Ratio({L})'] = np.log(self.DF['Close'] / self.DF[f'SMA({L})'])
        self.DF['FP'] = self.DF['Open'].shift(-1)
        self.DF.dropna(inplace=True)
        self.nD = len(self.DF)
    def Trade(self, Parameters:np.ndarray):
        Moneys = np.zeros(self.nD)
        Shares = np.zeros(self.nD)
        Values = np.zeros(self.nD)
        Signals = np.zeros(self.nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        money = 1
        share = 0
        for i in range(self.nD):
            fp = self.DF['FP'][i]
            lr = self.DF[f'Log-Ratio({self.L})'][i]
            signal = Parameters[0] + Parameters[1] * lr
            if signal > 0 and share == 0:
                share = money / fp
                money = 0
                Buys['Time'].append(i)
                Buys['Price'].append(fp)
            elif signal  0:
                money = share * fp
                share = 0
                Sells['Time'].append(i)
                Sells['Price'].append(fp)
            Moneys[i] = money
            Shares[i] = share
            Values[i] = money + share * fp
            Signals[i] = signal
        Return = 100 * ((Values[-1] / Values[0])**(1 / (self.nD - 1)) - 1)
        return Moneys, Shares, Values, Signals, Buys, Sells, Return
    def Loss(self, P:np.ndarray):
        Return = self.Trade(P)[-1]
        self.TrainLog.append(Return)
        return -Return
    def Train(self, MaxIteration:int, SwarmSize:int):
        lb = -1 * np.ones(2)
        ub = +1 * np.ones(2)
        self.P, BestLoss = ps.pso(self.Loss,
                                  lb,
                                  ub,
                                  swarmsize=SwarmSize,
                                  maxiter=MaxIteration)
        BestReturn = -BestLoss
        print('_'*50)
        print('Optimization Result:')
        print(f'tBest Parameters: {self.P}')
        print(f'tBest Return: {BestReturn} %')
        print('_'*50)

فیلم آموزش پیاده سازی اندیکاتورهای تکنیکال با پایتون Python – بخش یکم در تم آف

کلیک کنید

حال نیاز داریم متد سازنده را اصلاح کنیم. برای جدا کردن مجموعه داده به دو بخش آموزش و آزمایش که نسبت اندازه مجموعه داده آموزش به کل عدد تعیین‌کننده در جداسازی مجموعه داده خواهد بود. این عدد در ورودی متد سازنده دریافت خواهد شد:

    def __init__(self, sTrain:float=0.8):

حال، کد قبلی را حفظ کرده و در انتها این نسبت را در شی ذخیره می‌کنیم:

    def __init__(self, sTrain:float=0.8):
        self.TrainLog = []
        self.sTrain = sTrain

متد بعدی با اسم GetData نیاز به تغییرات ندارد، زیرا قبل از فرایند تقسیم داده و پردازش است.

برای یادگیری برنامه‌نویسی با زبان پایتون، پیشنهاد می‌کنیم به مجموعه آموزش‌های مقدماتی تا پیشرفته پایتون تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه آموزش‌های برنامه نویسی پایتون (Python) — مقدماتی تا پیشرفته + اینجا کلیک کنید.

متد بعدی با اسم ProcessData نیاز است تا تغییر کند و دو دیتافریم برای مجموعه داده آموزش و آزمایش ایجاد شود. در انتهای کد قبلی، دیتافریم کامل ایجاد می‌شود و تنها نیاز است سایز هر مجموعه را محاسبه کنیم:

    def ProcessData(self, L:int):
        self.L = L
        self.DF[f'SMA({L})'] = self.DF['Close'].rolling(L).mean()
        self.DF[f'Log-Ratio({L})'] = np.log(self.DF['Close'] / self.DF[f'SMA({L})'])
        self.DF['FP'] = self.DF['Open'].shift(-1)
        self.DF.dropna(inplace=True)
        self.nD = len(self.DF)
        self.nDtr = round(self.sTrain * self.nD)
        self.nDte = self.nD - self.nDtr

حال می‌توانیم nDtr سطر اول دیتافریم را برای آموزش و بقیه را برای آزمایش جدا می‌کنیم:

    def ProcessData(self, L:int):
        self.L = L
        self.DF[f'SMA({L})'] = self.DF['Close'].rolling(L).mean()
        self.DF[f'Log-Ratio({L})'] = np.log(self.DF['Close'] / self.DF[f'SMA({L})'])
        self.DF['FP'] = self.DF['Open'].shift(-1)
        self.DF.dropna(inplace=True)
        self.nD = len(self.DF)
        self.nDtr = round(self.sTrain * self.nD)
        self.nDte = self.nD - self.nDtr
        self.trDF = self.DF.iloc[:self.nDtr, :]
        self.teDF = self.DF.iloc[self.nDtr:, :]

به این ترتیب، دو مجموعه داده از یکدیگر جدا و در شی ذخیره می‌شوند.

حال می‌توانیم تابع مربوط به Trade را نیز اصلاح کنیم. با توجه به اینکه دو مجموعه داده وجود دارد، باید در ورودی تابع، مجموعه داده مورد استفاده را نیز تعریف کنیم. به این ترتیب، خواهیم داشت:

    def Trade(self, Parameters:np.ndarray, DF:pd.core.frame.DataFrame):

حال، باید اندازه دیتافریم را محاسبه کنیم:

    def Trade(self, Parameters:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)

حال آرایه (Array) و دیکشنری‌های (Dictionary) مربوط به تاریخچه را ایجاد می‌کنیم:

    def Trade(self, Parameters:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Signals = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}

حال همانند روندی که در برنامه گذشته وجود داشت، سرمایه اولیه و سهام اولیه را تعریف و حلقه اصلی مربوط به انجام معامله را ایجاد می‌کنیم:

    def Trade(self, Parameters:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Signals = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        money = 1
        share = 0
        for i in range(nD):

حال داده‌های مربوط به روز را استخراج و سیگنال را محاسبه می‌کنیم:

    def Trade(self, Parameters:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Signals = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        money = 1
        share = 0
        for i in range(nD):
            fp = DF['FP'][i]
            lr = DF[f'Log-Ratio({self.L})'][i]
            signal = Parameters[0] + Parameters[1] * lr

حال در مورد روز موردنظر تصمیم‌گیری کرده و در انتها موارد موردنظر را در تاریخچه ذخیره می‌کنیم:

    def Trade(self, Parameters:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Signals = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        money = 1
        share = 0
        for i in range(nD):
            fp = DF['FP'][i]
            lr = DF[f'Log-Ratio({self.L})'][i]
            signal = Parameters[0] + Parameters[1] * lr
            if signal > 0 and share == 0:
                share = money / fp
                money = 0
                Buys['Time'].append(i)
                Buys['Price'].append(fp)
            elif signal  0:
                money = share * fp
                share = 0
                Sells['Time'].append(i)
                Sells['Price'].append(fp)
            Moneys[i] = money
            Shares[i] = share
            Values[i] = money + share * fp
            Signals[i] = signal

در نهایت نیز میانگین درصد سود روزانه را محاسبه کرده و به همراه تاریخچه برمی‌گردانیم:

    def Trade(self, Parameters:np.ndarray, DF:pd.core.frame.DataFrame):
        nD = len(DF)
        Moneys = np.zeros(nD)
        Shares = np.zeros(nD)
        Values = np.zeros(nD)
        Signals = np.zeros(nD)
        Buys = {'Time':[], 'Price':[]}
        Sells = {'Time':[], 'Price':[]}
        money = 1
        share = 0
        for i in range(nD):
            fp = DF['FP'][i]
            lr = DF[f'Log-Ratio({self.L})'][i]
            signal = Parameters[0] + Parameters[1] * lr
            if signal > 0 and share == 0:
                share = money / fp
                money = 0
                Buys['Time'].append(i)
                Buys['Price'].append(fp)
            elif signal  0:
                money = share * fp
                share = 0
                Sells['Time'].append(i)
                Sells['Price'].append(fp)
            Moneys[i] = money
            Shares[i] = share
            Values[i] = money + share * fp
            Signals[i] = signal
        Return = 100 * ((Values[-1] / Values[0])**(1 / (nD - 1)) - 1)
        return Moneys, Shares, Values, Signals, Buys, Sells, Return

به این ترتیب، متد را به گونه‌ای تغییر می‌دهیم که به جای self.DF از دیتافریم ورودی استفاده کند. متد بعدی که باید اصلاح شود، مربوط به تابع هزینه است که با اسم Loss تعریف شده. این متد نیز باید در ورودی علاوه بر پارامترها، دیتافریم را نیز دریافت کند:

    def Loss(self, P:np.ndarray, DF:pd.core.frame.DataFrame):

حال می‌توانیم فراخوانی متد Trade را نیز اصلاح کنیم و ادامه تابع را بدون تغییر داشته باشیم:

    def Loss(self, P:np.ndarray, DF:pd.core.frame.DataFrame):
        Return = self.Trade(P, DF)[-1]
        self.TrainLog.append(Return)
        return -Return

به این ترتیب، این متد اصلاح می‌شود. تنها متد باقی‌مانده، مربوط به Train است. این تابع در ورودی نیازی به تغییر ندارد و تنها باید برای الگوریتم بهینه‌ساز، ورودی دیگری تعریف کنیم که دیتافریم آموزش را به تابع هزینه پاس دهد:

    def Train(self, MaxIteration:int, SwarmSize:int):
        lb = -1 * np.ones(2)
        ub = +1 * np.ones(2)
        self.P, BestLoss = ps.pso(self.Loss,
                                  lb,
                                  ub,
                                  swarmsize=SwarmSize,
                                  maxiter=MaxIteration,
                                  args=(self.trDF, ))
        BestReturn = -BestLoss
        print('_'*50)
        print('Optimization Result:')
        print(f'tBest Parameters: {self.P}')
        print(f'tBest Return: {BestReturn} %')
        print('_'*50)

به این ترتیب، همه متدهای مربوط به کلاس اصلاح می‌شود. حال تنظیمات زیر را اعمال می‌کنیم:

np.random.seed(0)
plt.style.use('ggplot')

حال از کلاس اصلاح شده یک شی ایجاد می‌کنیم:

Trader = smaLR()

حال مجموعه داده را دریافت، پردازش‌های مورد نیاز را اعمال و در نهایت مدل را آموزش می‌دهیم:

Trader.GetData('BTC-USD', '2017-01-01', '2022-04-01')

Trader.ProcessData(40)

Trader.Train(30, 40)

در کد فوق، سه مرحله زیر انجام می‌شود:

1. مجموعه داده مربوط به قیمت بیتکوین (Bitcoin) بین دو تاریخ 2017/01/01 تا 2022-04-01 دریافت می‌شود.
2. میانگین متحرک ساده (Simple Moving Average | SMA) بر روی قیمت اعمال و لگاریتم نسبت قیمت به میانگین متحرک ساده محاسبه می‌شود.
3. سپس، مجموعه داده آموزش و آزمایش از یکدیگر جدا می‌شود.

فیلم آموزش میانگین متحرک – تحلیل تکنیکال در بورس و سرمایه گذاری در بازارهای مالی با Moving Average در تم آف

کلیک کنید

الگوریتم بهینه‌سازی ازدحام ذرات (Particle Swarm Optimization | PSO) با 80 ذره به تعداد 60 مرحله کار می‌کند و پارامترهای ربات بهینه می‌شود.

پس از اجرا، نتایج زیر حاصل می‌شود:

Optimization Result:
        Best Parameters: [-0.00424805  0.34820413]
        Best Return: 0.30380404578569387 %

به این ترتیب، میانگین درصد سود روزانه 0/3038 % حاصل شده است. حال می‌توانیم همانند مطلب گذشته، نمودار سود در طول آموزش مدل را رسم کنیم:

plt.plot(Trader.TrainLog, ls='-', lw=0.8, c='crimson')
plt.title('Model Return Over Function Evaluations')
plt.xlabel('Function Evaluation')
plt.ylabel('Average Daily Return (%)')
plt.show()

که پس از اجرا، شکل زیر را خواهیم داشت.

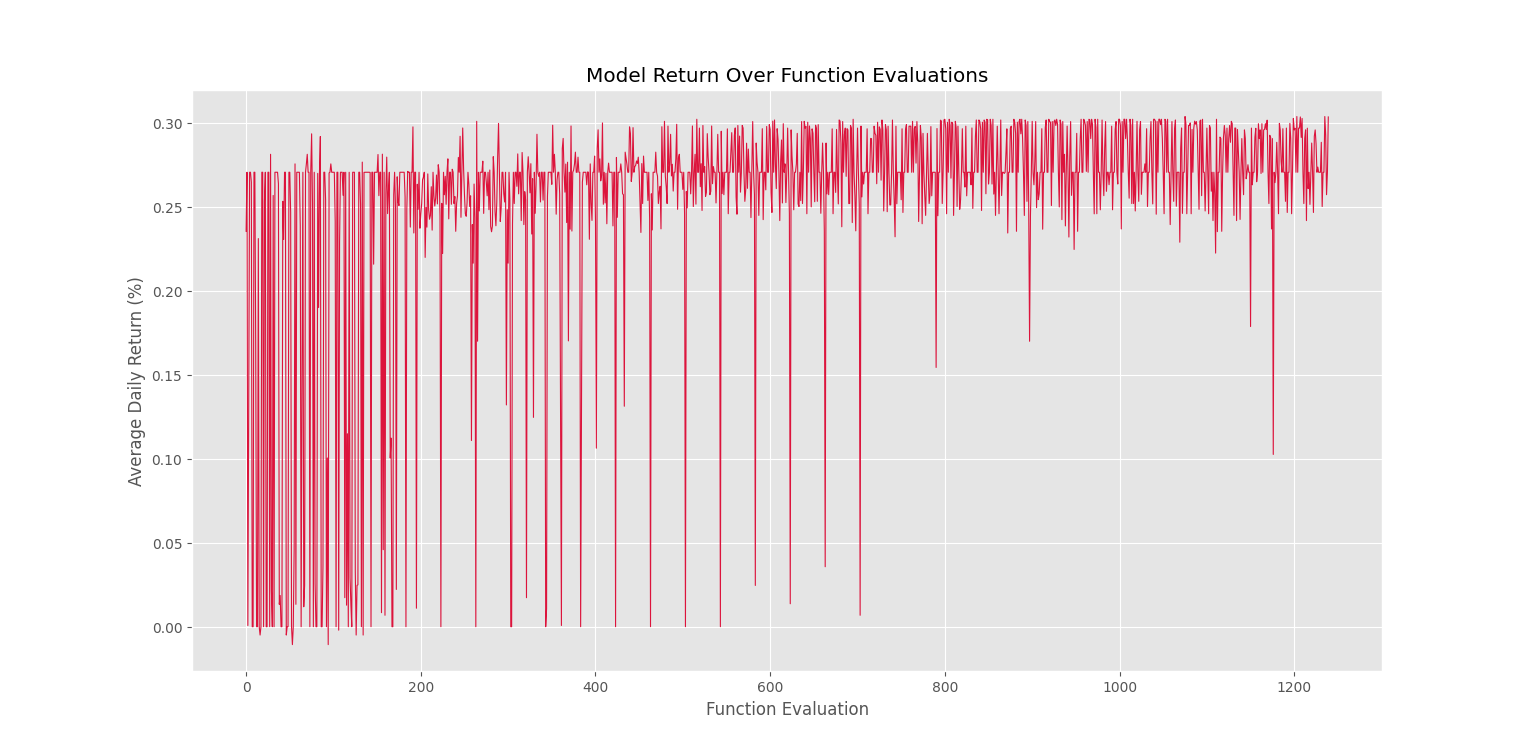
به این ترتیب، روند بهبود رفتار ربات کاملاً مشهود است. حال می‌توانیم ربات را روی مجموعه داده آموزش و آزمایش اجرا کرده و تاریخچه را دریافت کنیم:

_, _, trValues, trSignals, trBuys, trSells, trReturn = Trader.Trade(Trader.P, Trader.trDF)
_, _, teValues, teSignals, teBuys, teSells, teReturn = Trader.Trade(Trader.P, Trader.teDF)

حال می‌توانیم نمودار قیمت، میانگین متحرک و ارزش پرتفوی را همانند قبل رسم کنیم:

plt.subplot(1, 2, 1)
plt.semilogy(Trader.trDF['Close'].to_numpy(), ls='-', lw=0.8, c='k', label='Close')
plt.semilogy(Trader.trDF[f'SMA({Trader.L})'].to_numpy(), ls='-', lw=1, c='b', label=f'SMA({Trader.L})')
plt.title('Price Over Time (Train)')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()

plt.subplot(1, 2, 2)
trMeanValue = (1 + trReturn / 100)**np.arange(start=0, stop=trValues.size, step=1)
plt.semilogy(trValues, ls='-', lw=0.8, c='crimson', label='Real Values')
plt.semilogy(trMeanValue, ls='--', lw=1, c='k', label=f'Mean Values (Return: {round(trReturn, 4)} %)')
plt.title('Value Over Time (Train)')
plt.xlabel('Time (Day)')
plt.ylabel('Value')
plt.legend()

plt.show()

که شکل زیر را خواهیم داشت.

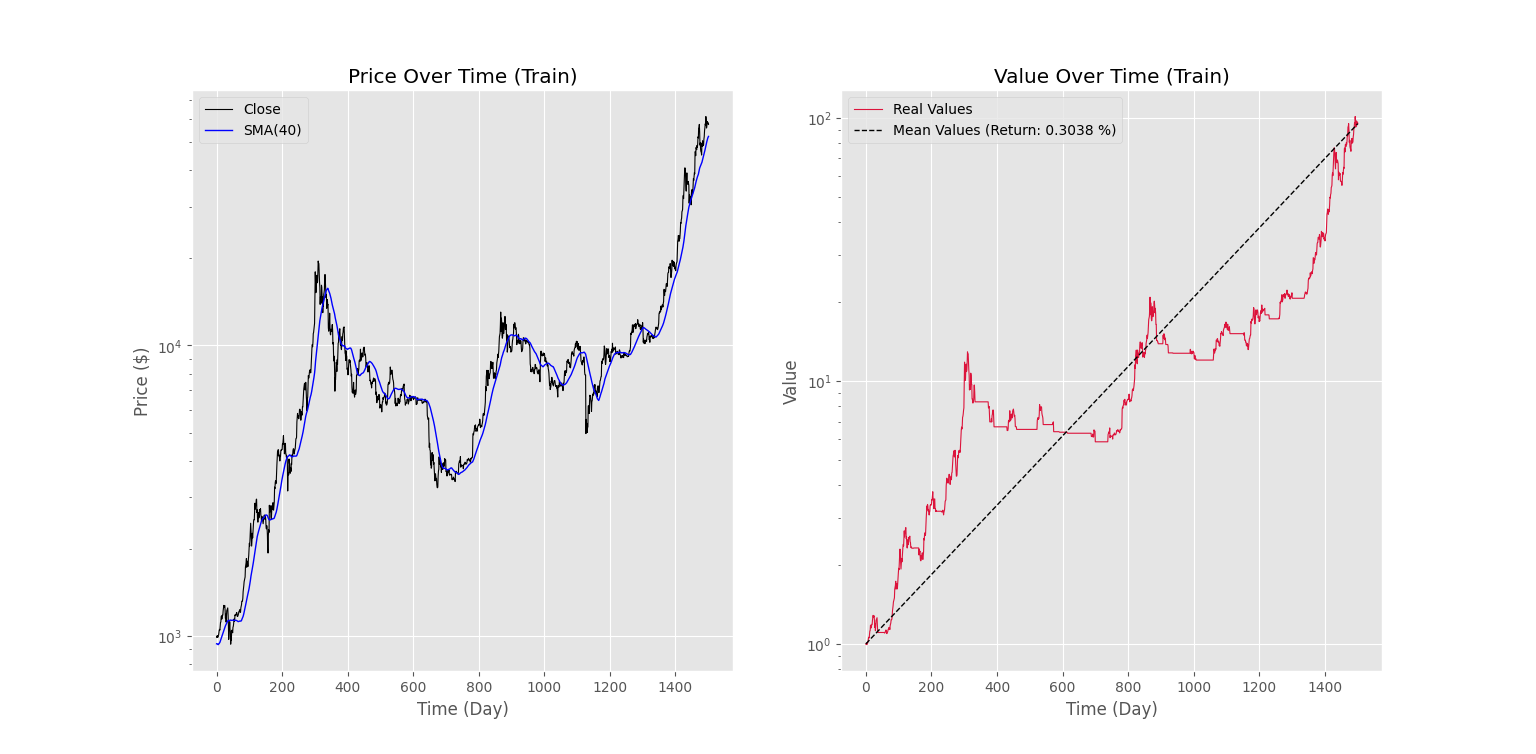
به این ترتیب، مشاهده می‌کنیم که ربات به خوبی توانسته روندها را شناسایی کند، و مانع از ضرر شود. توجه داشته باشید که ربات در طول مدت 1500 روز، توانسته سرمایه اولیه را به حدود 100 برابر مقدار اولیه برساند!

حال می‌توانیم برای نمایش مقدار سیگنال در طول این بازه، به شکل زیر عمل کنیم:

plt.subplot(3, 1, (1, 2))
plt.semilogy(Trader.trDF['Close'].to_numpy(), ls='-', lw=0.8, c='k', label='Close')
plt.semilogy(Trader.trDF[f'SMA({Trader.L})'].to_numpy(), ls='-', lw=1, c='b', label=f'SMA({Trader.L})')
plt.title('Price Over Time (Train)')
plt.ylabel('Price ($)')
plt.legend()

plt.subplot(3, 1, 3)
trZ = np.zeros_like(trSignals)
plt.plot(trSignals, ls='-', lw=0.7, c='k')
plt.fill_between(np.arange(trSignals.size), trSignals, trZ, where=(trSignals > trZ), color='lime', alpha=0.9, label='Buy Signal')
plt.fill_between(np.arange(trSignals.size), trSignals, trZ, where=(trSignals 

با اجرای کد، نمودار زیر نمایش داده خواهد شد.

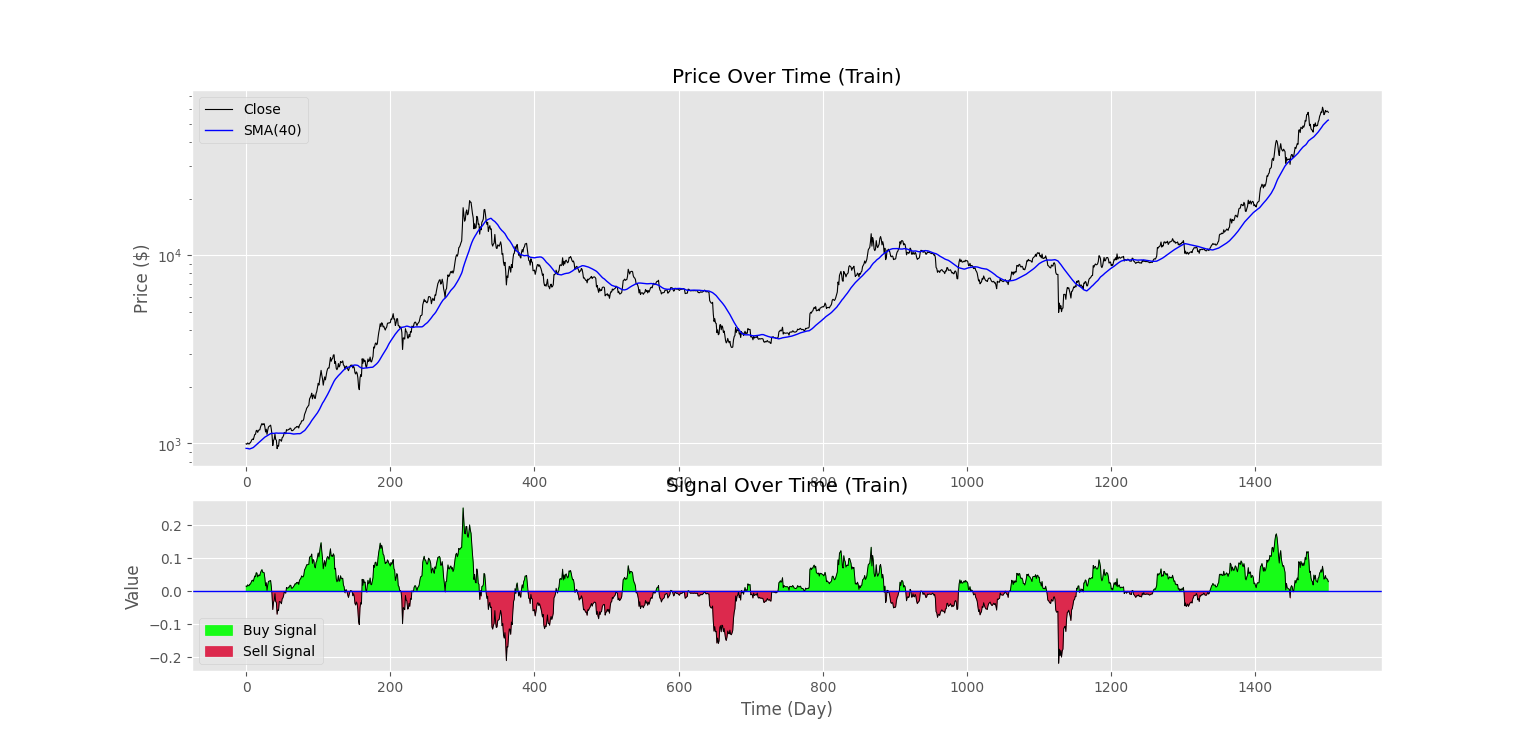
به این ترتیب، تطابق نمودار سیگنال با رفتار و روند بازار مشهود است. توجه داشته باشید که به دلیل کوتاه بودن طول میانگین متحرک (L=40)، معاملات ربات نیز بیشتر تحت تأثیر نوسان‌های کوتاه‌مدت (Short Term) قرار می‌گیرد، درحالیکه برای L=60 این نوسان‌های کوتاه‌مدت کمتر بود. تأثیرپذیری ربات از نوسان‌های کوتاه‌مدت، نقطه‌ضعف مدل نیست، چرا که می‌تواند سود بیشتری به همراه داشته باشد. به همین دلیل، تعیین طول پنجره اندیکاتورهای مورد استفاده مهم است.

برای نمایش نقاط خرید و فروش نیز، به شکل زیر عمل می‌کنیم:

plt.semilogy(Trader.trDF['Close'].to_numpy(), ls='-', lw=0.8, c='k', label='Close')
plt.semilogy(Trader.trDF[f'SMA({Trader.L})'].to_numpy(), ls='-', lw=1, c='b', label=f'SMA({Trader.L})')
plt.scatter(trBuys['Time'], trBuys['Price'], s=20, c='g', marker='o', label='Buy')
plt.scatter(trSells['Time'], trSells['Price'], s=20, c='r', marker='o', label='Sell')
plt.title('Price Over Time (Train)')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.legend()
plt.show()

و نمودار زیر به خوبی این نقاط را نشان می‌دهد.

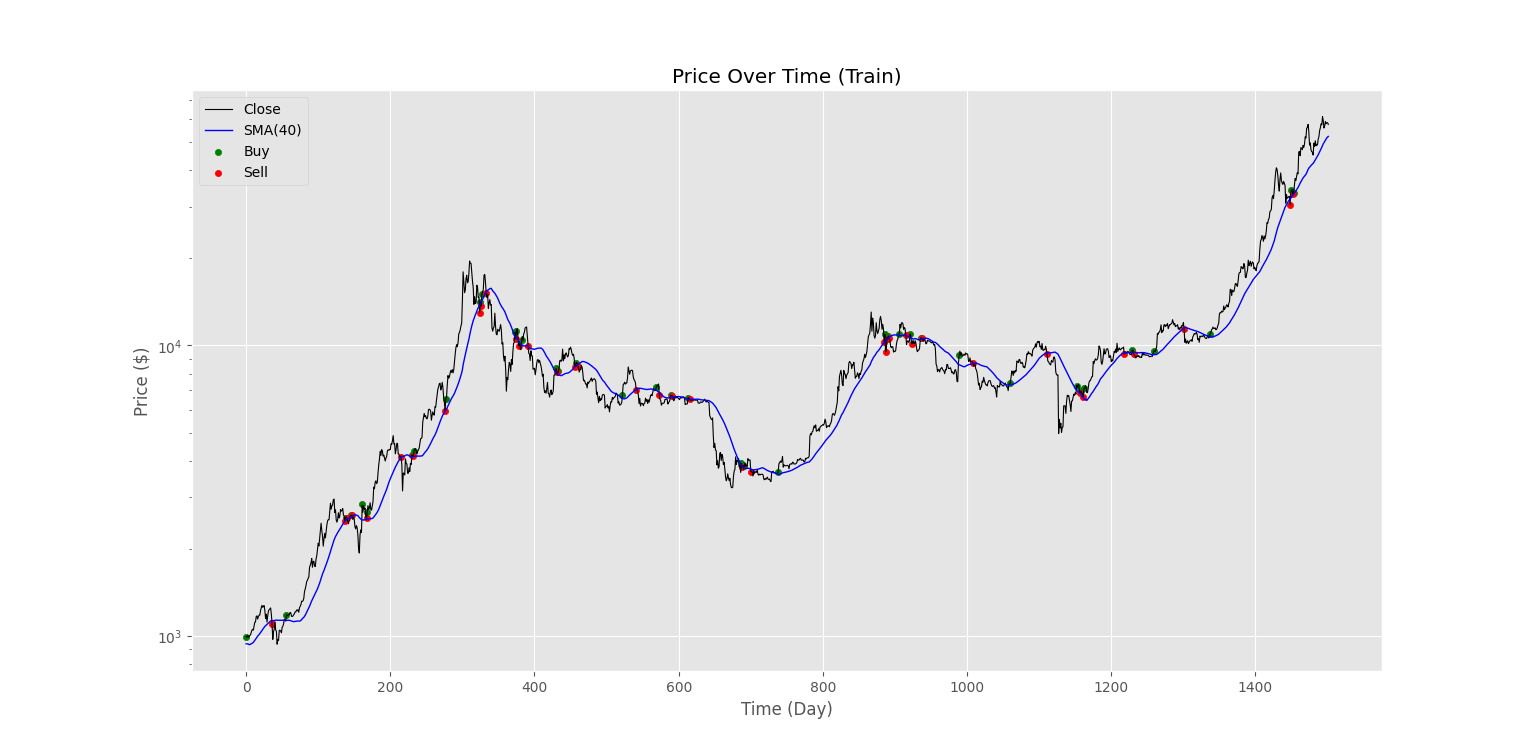
در نمودار بالا، خرید و فروش ربات در مواقع برخورد و شکست خط میانگین متحرک ساده مشاهده می‌شود. نکته مهم دیگری که وجود دارد، این است که تعداد معاملات بالا و عکس هم در محل برخورد با میانگین متحرک ساده است. این اتفاق در دنیای واقعی می‌تواند مشکل‌ساز باشد و نباید اجازه داد ربات با استناد به سیگنال‌های ضعیف، اقدام به معامله کند.

آزمایش مدل روی مجموعه داده آزمایش

به این ترتیب، 3 نمودار مهم برای مجموعه داده آموزش رسم و بررسی شد. حال نمودارهای آورده شده را برای مجموعه داده آزمایش نیز رسم می‌کنیم تا تعمیم‌پذیری (Generalizability) مدل را بررسی کنیم. در صورتی که ربات روی مجموعه داده آزمایش، به نتایج مشابه با مجموعه داده آموزش نرسد، به این نتیجه می‌رسیم که مدل قابل تعمیم نبود و در دنیای واقعی نتایج مورد انتظار را نخواهد گرفت.

فیلم آموزش پیاده سازی ربات معامله گر با مدل SVM در پایتون در تم آف

کلیک کنید

نمودار اول به شکل زیر حاصل می‌شود.

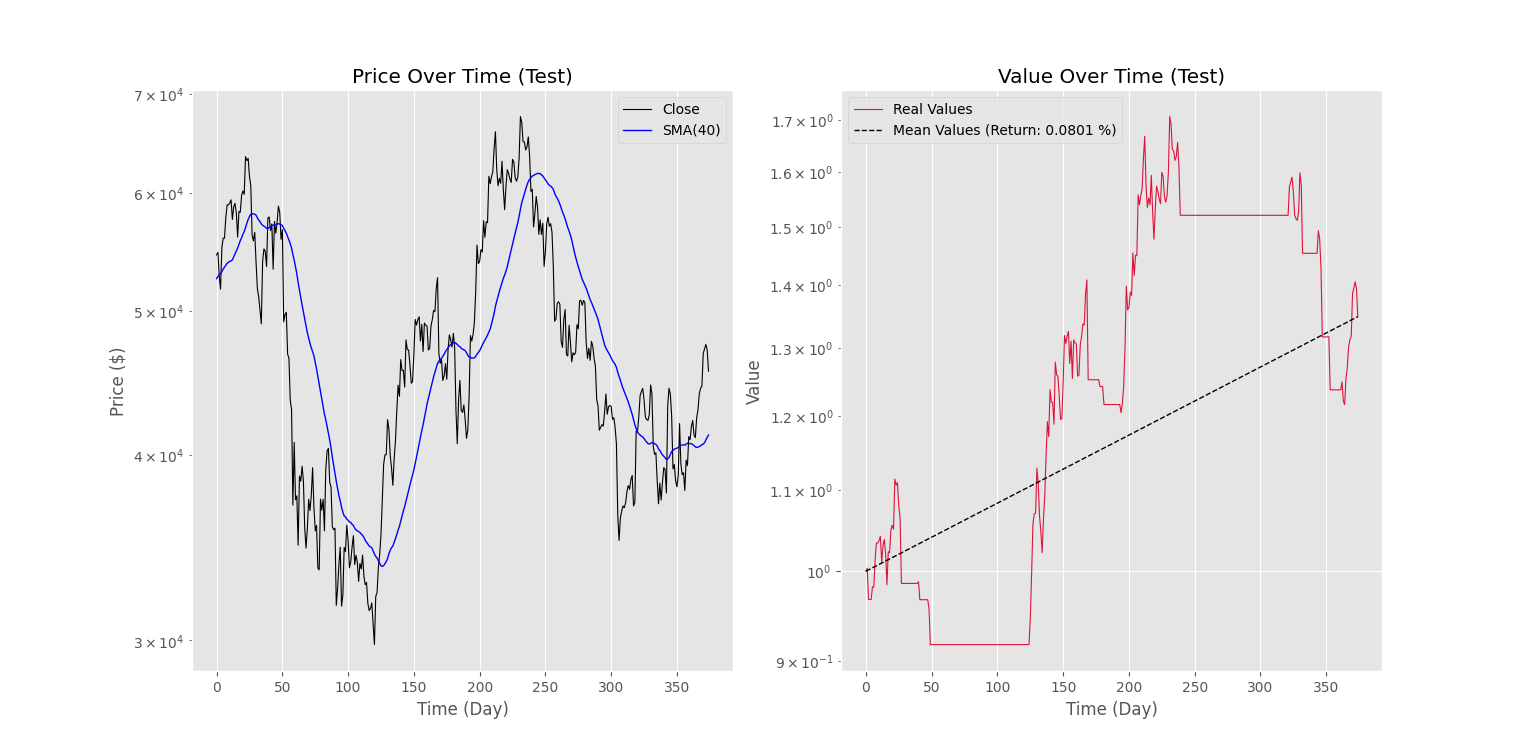
مشاهده می‌کنیم که میانگین درصد سود روزانه، برابر با 0.0801 % حاصل می‌شود که نسبت به مجموعه داده آموزش، کم است. البته باید به این نکته نیز توجه کرد که بخش بزرگی از این کاهش عملکرد، مربوط به شرایط نماد است. در 1500 روز مربوط به مجموعه داده آموزش، ارزش نماد 15 برابر شده است، ولی در 400 روز مربوط به مجوعه داده آزمایش، ارزش نماد 0.8 برابر شده است. به همین دلیل، می‌توان عملکرد مدل را قابل قبول دانست.

فیلم آموزش تجزیه و تحلیل داده های مالی با پایتون – بخش یکم در تم آف

کلیک کنید

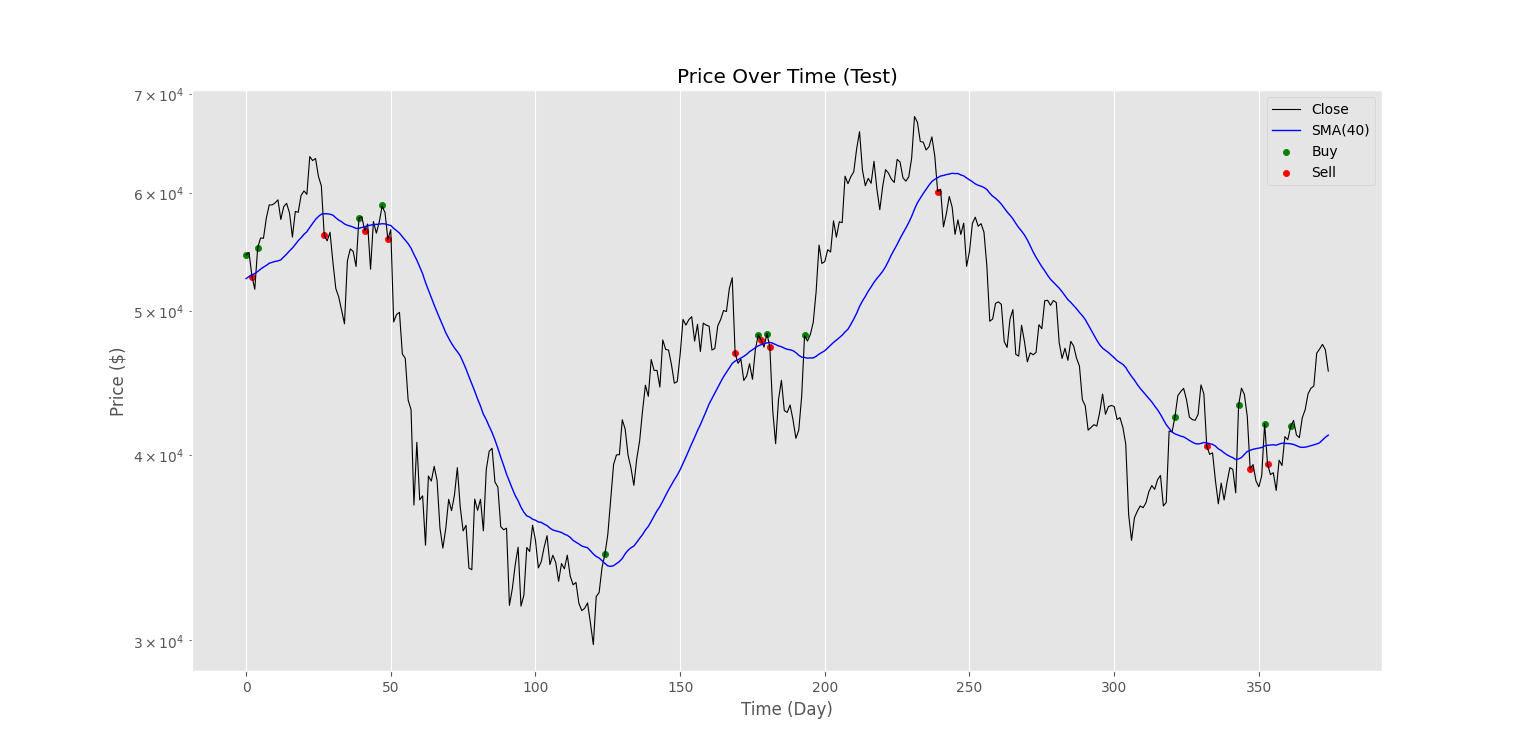
به همین دلیل، تنها اتکا به میانگین درصد سود روزانه، نمی‌تواند مناسب باشد و باید سود ربات نسبت به سود نماد سنجیده شود. توجه داشته باشید که در ربات در بازه‌هایی دچار ضرر نیز شده است و بخشی از سرمایه اول خود را نیز از دست داده است. در روزهایی که ارزش پرتفوی، کمتر از 1 واحد بوده، ربات ضرر داشته است. نمودار دوم به شکل زیر حاصل می‌شود.

مشاهده می‌کنیم که همانند مجموعه داده آموزش، ربات به خوبی توانسته روند و جهت قیمت را شناسایی و پیش‌بینی کند.

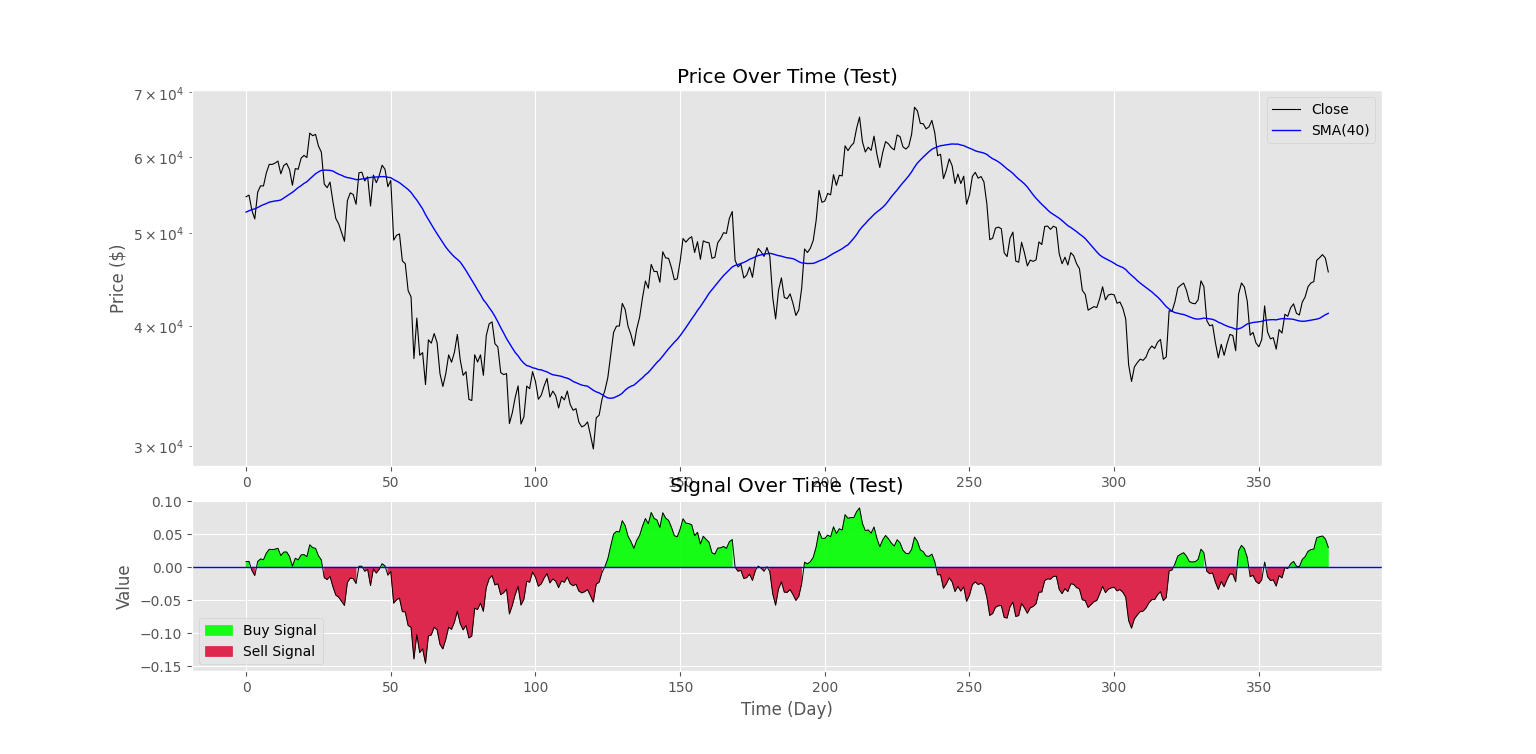
نمودار سوم به شکل زیر حاصل می‌شود.

به این ترتیب، مشاهده می‌کنیم که مدل در روندهای بلندمدت (Long Term)، سود مناسبی کسب کرده، ولی در شرایطی که بازار حالت نوسانی (Consolidation) و بدون روند (Range) داشته، اغلب معاملات دچار شکسته شده‌اند. به همین دلیل، نیاز است تا وجود روند در بازار و محاسبه دقت سیگنال، انجام شود.

جمع‌بندی

در این مطلب، به اهمیت مجموعه داده آزمایش و روش تقسیم مجموعه داده پرداختیم. برای مطالعه بیشتر، می‌توان موارد زیر را بررسی کرد:

1. چگونه می‌توان از انجام معاملات فراوان توسط ربات جلوگیری کرد؟
2. شرایط نوسانی در بازار را چگونه می‌توان شناسایی کرد؟
3. برای رسم نمودارهای آورده‌شده، متدهای در کلاس نوشته شده بنویسید که فرایند کدنویسی و رسم نمودار را تسهیل کنند.
4. برای بررسی شرایط ربات در طول آموزش، یک مجموعه داده اعتبارسنجی (Validation Dataset) ایجاد کنید و بهینه‌ترین مقدار Max Iteration و Swarm Size را بیابید.