ساخت ربات معامله گر رمزارز با استفاده از اسیلاتور استوکستیک — پیاده سازی در پایتون

در مطالب گذشته مجله تم آف، به ساخت ربات معاملهگر با استفاده از میانگین متحرک ساده (Simple Moving Average | SMA) و تقسیم مجموعه داده پرداختیم. در این مطلب، قصد داریم یک ربات معاملهگر با استفاده از اسیلاتور استوکستیک (Stochastic Oscillator) میپردازیم که یک اندیکاتور (Indicator) نوسانگر است.

اسیلاتور استوکستیک
این اندیکاتور موقعیت قیمت فعلی نسبت به بیشترین و کمترین قیمت مشاهده شده در L دوره گذشته را نشان میدهد. برای محاسبه خط K خواهیم داشت:
$$begin{aligned}
&L L_{t}=min left(left{L o w_{i} mid t-L+1 leq i leq tright}right) \
&H H_{t}=max left(left{H i g h_{i} mid t-L+1 leq i leq tright}right) \
&K_{t}=100 times frac{text { close }_{t}-L L_{t}}{H H_{t}-L L_{t}}
end{aligned}$$
خط K همواره عددی بین 0 و 100 است. اعداد بین 0 تا 30 نشاندهنده بیشفروش (Oversold) است و انتظار صعود قیمت را در آینده داریم. اعداد بین 70 تا 100 نیز نشاندهنده بیشخرید (Overbought) است و انتظار نزول قیمت را در آینده داریم.
سپس، یک خط D به صورت میانگین متحرک ساده 3 روزه از روی K محاسبه میشود:
$$D_t=SMA_t (K,3) $$
به خط K استوکستیک سریع (Fast Stochastic) و به خط D استوکستیک آرام (Slow Stochastic) گفته میشود.
تقاطع خط K با خط D به سمت بالا، سیگنال برای خرید میباشد و برعکس آن، تقاطع خط K با خط D به سمت پایین، سیگنال برای فروش است.
به این ترتیب، اختلاف خط K و خط D میتواند معیار مناسبی به عنوان سیگنال باشد:
$$ Signal _ t = K_t-D_t $$
برای پیادهسازی ربات، وارد محیط برنامهنویسی پایتون میشویم و کتابخانههای مورد نیاز را فراخوانی میکنیم:
import numpy as np
import pandas as pd
import pandas_datareader as pdt
import matplotlib.pyplot as plt
این کتابخانهها در کدنویسی به ترتیب برای موارد زیر استفاده خواهند شد:
- محاسبات برداری (Vectorized Calculation) و استفاده از آرایهها (Array)
- کار با دیتافریمها (Dataframe)
- دریافت آنلاین (Online) مجموعه داده مربوط به تاریخچه قیمتی (Historical Price) نمادها
- رسم نمودار قیمت، سیگنال و نقاط خرید و فروش ربات
حال تنظیمات مربوط به Randomness و Style را اعمال میکنیم:
np.random.seed(0)
plt.style.use('ggplot')پیادهسازی کلاس
یک کلاس مربوط به ربات ایجاد میکنیم:
class stcBot:این کلاس شامل 8 متد (Method) خواهد بود.
پیادهسازی متد سازنده
با توجه به اینکه طول پنجره محاسبه خط K به صورت دقیق معلوم نیست، باید بهینهسازی شود. به همین دلیل، حد بالا و پایین طول پنجره خط K، به همراه طول میانگین متحرک مربوط به خط D و در نهایت نسبت اندازه مجموعه داده آموزش (Train Dataset) به کل مجموعه داده در ورودی متن سازنده دریافت خواهند شد:
def __init__(self, Ld:int=5, MinL:int=2, MaxL:int=200, sTrain:float=0.6):حال موارد دریافتشده را در شی (Object) که با نام self میشناسیم، ذخیره میکنیم:
def __init__(self, Ld:int=4, MinL:int=2, MaxL:int=200, sTrain:float=0.6):
self.Ld = Ld
self.MinL = MinL
self.MaxL = MaxL
self.sTrain = sTrain
به این ترتیب، کد این متد کامل میشود.
پیادهسازی متد دریافت داده
این متد در ورودی اسم نماد، تاریخ شروع داده و تاریخ اتمام داده را دریافت میکند:
def GetData(self, Ticker:str, Start:str, End:str):حال ورودیهای دریافتشده را ذخیره و سپس مجموعه داده را با استفاده از کتابخانه Pandas Datareader دریافت میکنیم:
def GetData(self, Ticker:str, Start:str, End:str):
self.Ticker = Ticker
self.Start = Start
self.End = End
self.DF = pdt.DataReader(Ticker,
data_source='yahoo',
start=Start,
end=End)دو ستون Volume و Adj Close مورد نیاز نبوده و آنها را حذف میکنیم:
def GetData(self, Ticker:str, Start:str, End:str):
self.Ticker = Ticker
self.Start = Start
self.End = End
self.DF = pdt.DataReader(Ticker,
data_source='yahoo',
start=Start,
end=End)
self.DF.drop(labels=['Volume', 'Adj Close'],
axis=1,
inplace=True)به این ترتیب، مجموعه داده به راحتی دریافت و در شی ذخیره میشود.
پیادهسازی متد پردازش داده
این متد عملیاتی روی مجموعه داده خام (Raw Dataset) انجام میدهد و آن را به شکل قابل استفاده درمیآورد. با توجه به اینکه نیاز داریم تا تمامی Lهای بین$$L_min$$ و$$L_max$$ را بررسی کنیم، باید با استفاده از یک حلقه، برای تمامی Lها اندیکاتور را محاسبه کنیم:
def ProcessData(self):
for L in range(self.MinL, self.MaxL+1):
حال دو ستون LL و HH را با استفاده از متدهای rolling, min, max محاسبه میکنیم:
def ProcessData(self):
for L in range(self.MinL, self.MaxL+1):
self.DF['LL'] = self.DF['Low'].rolling(L).min()
self.DF['HH'] = self.DF['High'].rolling(L).max()حال میتوانیم خط K، خط D و سیگنال نهایی را محاسبه کنیم:
def ProcessData(self):
for L in range(self.MinL, self.MaxL+1):
self.DF['LL'] = self.DF['Low'].rolling(L).min()
self.DF['HH'] = self.DF['High'].rolling(L).max()
self.DF['K'] = (self.DF['Close'] - self.DF['LL']) / (self.DF['HH'] - self.DF['LL'])
self.DF['D'] = self.DF[f'K'].rolling(self.Ld).mean()
self.DF[f'Signal({L})'] = self.DF['K'] - self.DF['D']سپس ستونهای اضافی را حذف میکنیم:
def ProcessData(self):
for L in range(self.MinL, self.MaxL+1):
self.DF['LL'] = self.DF['Low'].rolling(L).min()
self.DF['HH'] = self.DF['High'].rolling(L).max()
self.DF['K'] = (self.DF['Close'] - self.DF['LL']) / (self.DF['HH'] - self.DF['LL'])
self.DF['D'] = self.DF[f'K'].rolling(self.Ld).mean()
self.DF[f'Signal({L})'] = self.DF['K'] - self.DF['D']
self.DF.drop(['LL', 'HH', 'K', 'D'], axis=1, inplace=True)به این ترتیب، برای هر L خط سیگنال محاسبه و به دیتافریم افزوده میشود.
حال نیاز داریم تا قیمت اولین فرصت خرید در روز مربوط را محاسبه کنیم:
def ProcessData(self):
for L in range(self.MinL, self.MaxL+1):
self.DF['LL'] = self.DF['Low'].rolling(L).min()
self.DF['HH'] = self.DF['High'].rolling(L).max()
self.DF['K'] = (self.DF['Close'] - self.DF['LL']) / (self.DF['HH'] - self.DF['LL'])
self.DF['D'] = self.DF[f'K'].rolling(self.Ld).mean()
self.DF[f'Signal({L})'] = self.DF['K'] - self.DF['D']
self.DF.drop(['LL', 'HH', 'K', 'D'], axis=1, inplace=True)
self.DF['FP'] = self.DF['Open'].shift(-1)با توجه به اینکه برخی ستونها برای برخی سطرها از مجموعه داده، مقدار Nan یا Not a Number به خود میگیرند، باید آنها را حذف کنیم. بنابراین، خواهیم داشت:
def ProcessData(self):
for L in range(self.MinL, self.MaxL+1):
self.DF['LL'] = self.DF['Low'].rolling(L).min()
self.DF['HH'] = self.DF['High'].rolling(L).max()
self.DF['K'] = (self.DF['Close'] - self.DF['LL']) / (self.DF['HH'] - self.DF['LL'])
self.DF['D'] = self.DF[f'K'].rolling(self.Ld).mean()
self.DF[f'Signal({L})'] = self.DF['K'] - self.DF['D']
self.DF.drop(['LL', 'HH', 'K', 'D'], axis=1, inplace=True)
self.DF['FP'] = self.DF['Open'].shift(-1)
self.DF.dropna(inplace=True)حال میتوانیم اندازه نهایی مجموعه داده را محاسبه و سپس مجموعه داده را به دو قسمت آموزش (Train) و آزمایش (Test) تقسیم میکنیم:
def ProcessData(self):
for L in range(self.MinL, self.MaxL+1):
self.DF['LL'] = self.DF['Low'].rolling(L).min()
self.DF['HH'] = self.DF['High'].rolling(L).max()
self.DF['K'] = (self.DF['Close'] - self.DF['LL']) / (self.DF['HH'] - self.DF['LL'])
self.DF['D'] = self.DF[f'K'].rolling(self.Ld).mean()
self.DF[f'Signal({L})'] = self.DF['K'] - self.DF['D']
self.DF.drop(['LL', 'HH', 'K', 'D'], axis=1, inplace=True)
self.DF['FP'] = self.DF['Open'].shift(-1)
self.DF.dropna(inplace=True)
self.nD = len(self.DF)
self.nDtr = round(self.sTrain * self.nD)
self.nDte = self.nD - self.nDtr
self.trDF = self.DF.iloc[:self.nDtr, :]
self.teDF = self.DF.iloc[self.nDtr:, :]به این ترتیب، این تابع سیگنالهای مورد نیاز را محاسبه، به دیتافریم اضافه و در نهایت مجموعه داده آموزش و آزمایش را ایجاد میکند.
پیادهسازی متد معامله
این متد در ورودی دیتافریم مربوط به مجموعه داده و طول پنجره اندیکاتور را دریافت میکند:
def Trade(self, DF:pd.core.frame.DataFrame, L:int):سپس، اندازه دیتافریم ورودی را محاسبه و آرایههای مورد نیاز برای ذخیره تاریخچه را ایجاد میکنیم:
def Trade(self, DF:pd.core.frame.DataFrame, L:int):
nD = len(DF)
Moneys = np.zeros(nD)
Shares = np.zeros(nD)
Values = np.zeros(nD)
Signals = np.zeros(nD)
Buys = {'Time':[], 'Price':[]}
Sells = {'Time':[], 'Price':[]}حال، سرمایه اولیه و سهام اولیه را تعیین میکنیم:
def Trade(self, DF:pd.core.frame.DataFrame, L:int):
nD = len(DF)
Moneys = np.zeros(nD)
Shares = np.zeros(nD)
Values = np.zeros(nD)
Signals = np.zeros(nD)
Buys = {'Time':[], 'Price':[]}
Sells = {'Time':[], 'Price':[]}
money = 1
share = 0سپس، به ازای هر روز از مجموعه داده، قیمت اولین فرصت خرید و سیگنال روز مربوطه را محاسبه میکنیم:
def Trade(self, DF:pd.core.frame.DataFrame, L:int):
nD = len(DF)
Moneys = np.zeros(nD)
Shares = np.zeros(nD)
Values = np.zeros(nD)
Signals = np.zeros(nD)
Buys = {'Time':[], 'Price':[]}
Sells = {'Time':[], 'Price':[]}
money = 1
share = 0
for i in range(nD):
fp = DF['FP'][i]
signal = DF[f'Signal({L})'][i]حال میتوانیم فرایند تصمیمگیری ربات را پیادهسازی کنیم. تصمیمگیری ربات در شرایط مختلف به شکل زیر خواهد بود:
| Signal | Signal=0 | Signal>0 | |
| Sell | Hold | Hold | Share>0 |
| Hold | Hold | Buy | Share=0 |
به این ترتیب، با پیادهسازی دو شرط منتهی به خرید و فروش، روند کامل خواهد بود:
def Trade(self, DF:pd.core.frame.DataFrame, L:int):
nD = len(DF)
Moneys = np.zeros(nD)
Shares = np.zeros(nD)
Values = np.zeros(nD)
Signals = np.zeros(nD)
Buys = {'Time':[], 'Price':[]}
Sells = {'Time':[], 'Price':[]}
money = 1
share = 0
for i in range(nD):
fp = DF['FP'][i]
signal = DF[f'Signal({L})'][i]
if signal > 0 and share == 0:
share = money / fp
money = 0
Buys['Time'].append(i)
Buys['Price'].append(fp)
elif signal 0:
money = share * fp
share = 0
Sells['Time'].append(i)
Sells['Price'].append(fp)حال میتوانیم تاریخچه و میانگین درصد سود روزانه را محاسبه و در خروجی متد برگردانیم:
def Trade(self, DF:pd.core.frame.DataFrame, L:int):
nD = len(DF)
Moneys = np.zeros(nD)
Shares = np.zeros(nD)
Values = np.zeros(nD)
Signals = np.zeros(nD)
Buys = {'Time':[], 'Price':[]}
Sells = {'Time':[], 'Price':[]}
money = 1
share = 0
for i in range(nD):
fp = DF['FP'][i]
signal = DF[f'Signal({L})'][i]
if signal > 0 and share == 0:
share = money / fp
money = 0
Buys['Time'].append(i)
Buys['Price'].append(fp)
elif signal 0:
money = share * fp
share = 0
Sells['Time'].append(i)
Sells['Price'].append(fp)
Moneys[i] = money
Shares[i] = share
Values[i] = money + share * fp
Signals[i] = signal
Return = 100 * ((Values[-1] / Values[0])**(1 / (nD - 1)) - 1)
return Moneys, Shares, Values, Signals, Buys, Sells, Returnبه این ترتیب، این متد کامل میشود.
پیادهسازی متد آموزش ربات
فرایند آموزش مدل، شامل تعیین بهترین مقدار L برای ربات است. طی این فرایند، به ازای هر L عملیات مربوط به معامله در مجموعه داده آموزش انجام و میانگین درصد سود روزانه ذخیره میشود.
ابتدا تمامی مقادیر L را محاسبه میکنیم و یک لیست خالی برای ذخیره میانگین درصد سود روزانه ایجاد میکنیم:
def Train(self):
self.Ls = np.arange(start=self.MinL, stop=self.MaxL + 1, step=1)
self.Rs = []حال با استفاده از یک حلقه، به ازای هر L تابع Trade فراخوانی و میانگین درصد سود روزانه به لیست Rs اضافه میکنیم:
def Train(self):
self.Ls = np.arange(start=self.MinL, stop=self.MaxL + 1, step=1)
self.Rs = []
for L in self.Ls:
R = self.Trade(self.trDF, L)[-1]
self.Rs.append(R)پس از اتمام حلقه، لیست Rs را به آرایه Numpy تبدیل میکنیم، سپس بیشترین میانگین درصد سود حاصل و بهترین L را ذخیره میکنیم و خروجی را نمایش میدهیم:
def Train(self):
self.Ls = np.arange(start=self.MinL, stop=self.MaxL + 1, step=1)
self.Rs = []
for L in self.Ls:
R = self.Trade(self.trDF, L)[-1]
self.Rs.append(R)
self.Rs = np.array(self.Rs)
self.BestReturn = self.Rs.max()
self.L = self.Ls[self.Rs.argmax()]
print('_' * 50)
print('Optimization Result:')
print(f'tBest L: {self.L}')
print(f'tBest Return: {self.BestReturn} %')
print('_' * 50)به این ترتیب، این متد بهترین L را برای ربات انتخاب و در شی ذخیره میکند.
تا به اینجا، 5 متد اصلی و مهم کلاس پیادهسازی شد. 3 متد بعدی مربوط به مصورسازی (Visualization) ربات هستند.
پیادهسازی متد رسم نمودار Return-L
این نمودار رابطه بین میانگین درصد سود روزانه با طول پنجره خط K را نشان میدهد. برای رسم این نمودار از دو آرایه Ls و Rs استفاده میکنیم:
def PlotRs(self):
plt.plot(self.Ls, self.Rs, ls='-', lw=0.8, c='teal', marker='o', ms=3, label='Points')
plt.scatter(self.L, self.BestReturn, s=50, marker='o', color='crimson', label='Best')
plt.title('Bot Return for Different Values of L')
plt.xlabel('L')
plt.ylabel('Average Daily Return (%)')
plt.legend()
plt.show()به این ترتیب، نمودار رسم شده و بهترین حالت مشخص میشود. این نمودار تنها با توجه به مجوعه داده آموزش رسم شده است.
پیادهسازی متد رسم نمودار Price-Time و Value-Time
این متد در ورودی مجموعه داده مورد نظر را دریافت خواهد کرد و سپس متد Trade روی آن اجرا خواهد شد:
def PlotValue(self, Data:str):
if Data == 'Train':
DF = self.trDF
elif Data == 'Test':
DF = self.teDF
_, _, Values, _, _, _, bReturn = self.Trade(DF, self.L)حال میتوانیم با استفاده از subplot در یک نمودار قیمت و میانگین سود حاصل را رسم کنیم. در نمودار دیگر نیز عملکرد ربات را نمایش میدهیم:
def PlotValue(self, Data:str):
if Data == 'Train':
DF = self.trDF
elif Data == 'Test':
DF = self.teDF
_, _, Values, _, _, _, bReturn = self.Trade(DF, self.L)
plt.subplot(1, 2, 1)
hReturn = 100 * ((DF['Close'][-1] / DF['Close'][0])**(1 / (len(DF) - 1)) - 1)
hMeanValue = DF['Close'][0] * (1 + hReturn / 100)**np.arange(start=0, stop=Values.size, step=1)
plt.plot(DF.index, DF['Close'], ls='-', lw=0.8, c='crimson', label='Close')
plt.plot(DF.index, hMeanValue, ls='--', lw=1, c='k', label=f'Mean Values (ADR: {round(hReturn, 4)} %)')
plt.title(f'Price Over Time ({Data})')
plt.xlabel('Time (Day)')
plt.ylabel('Price ($)')
plt.yscale('log')
plt.legend()
plt.subplot(1, 2, 2)
bMeanValue = (1 + bReturn / 100)**np.arange(start=0, stop=Values.size, step=1)
plt.plot(DF.index, Values, ls='-', lw=0.8, c='crimson', label='Real Values')
plt.plot(DF.index, bMeanValue, ls='--', lw=1, c='k', label=f'Mean Values (ADR: {round(bReturn, 4)} %)')
plt.title(f'Value Over Time ({Data})')
plt.xlabel('Time (Day)')
plt.ylabel('Value')
plt.yscale('log')
plt.legend()
plt.show()به این ترتیب، با استفاده از این متد میتوانیم برای مجموعه داده آموزش و آزمایش عملکرد ربات را در کنار عملکرد نماد رسم کنیم.
پیادهسازی متد رسم سیگنال
این متد، نمودار قیمت، نقاط ورود و خروج از نماد را به همراه نمودار سیگنال در زیر آن رسم میکند:
def PlotSignal(self, Data:str):
if Data == 'Train':
DF = self.trDF
elif Data == 'Test':
DF = self.teDF
_, _, _, Signals, Buys, Sells, _ = self.Trade(DF, self.L)
plt.subplot(3, 1, (1, 2))
plt.plot(DF.index, DF['Close'].to_numpy(), ls='-', lw=0.7, c='k', label='Close')
plt.scatter(DF.index[Buys['Time']], Buys['Price'], s=24, c='lime', marker='o', label='Buy')
plt.scatter(DF.index[Sells['Time']], Sells['Price'], s=24, c='crimson', marker='o', label='Sell')
plt.title(f'Price Over Time ({Data})')
plt.ylabel('Price ($)')
plt.yscale('log')
plt.tight_layout()
plt.legend()
plt.subplot(3, 1, 3)
Z = np.zeros_like(Signals)
plt.plot(DF.index, Signals, ls='-', lw=0.7, c='k')
plt.fill_between(DF.index, Signals, Z, where=(Signals > Z), color='lime', alpha=0.9, label='Buy Signal')
plt.fill_between(DF.index, Signals, Z, where=(Signals به این ترتیب، هر 8 متد مورد نیاز برای کلاس stcBot پیادهسازی شد. حال میتوانیم از کلاس ایجادشده استفاده کنیم.
استفاده از کلاس
حال یک شی از کلاس ایجاد میکنیم:
Trader = stcBot()سپس، مجموعه داده را دریافت میکنیم و پردازشهای مورد نیاز را انجام میدهیم:
Trader.GetData('BTC-USD', '2009-01-01', '2022-04-24')
Trader.ProcessData()سپس، مدل را آموزش میدهیم:
Trader.Train()که پس از اتمام آن، نتیجه به شکل زیر برگردانده میشود:
Optimization Result:
Best L: 80
Best Return: 0.2914800215035429 %به این ترتیب، مشاهده میکنیم که مقدار L=80 به عنوان بهترین طول پنجره استوکستیک سریع انتخاب شده است. در نتیجه استفاده از این طول پنجره، میانگین درصد سود روزانه برابر با 0.2914 % حاصل شده که مناسب است. باید توجه داشته که این سود تنها نشاندهنده عملکرد روی مجموعه داده آموزش است.
حال میتوانیم نمودار Return-L را رسم کنیم:
Trader.PlotRs()که شکل زیر را خواهیم داشت.
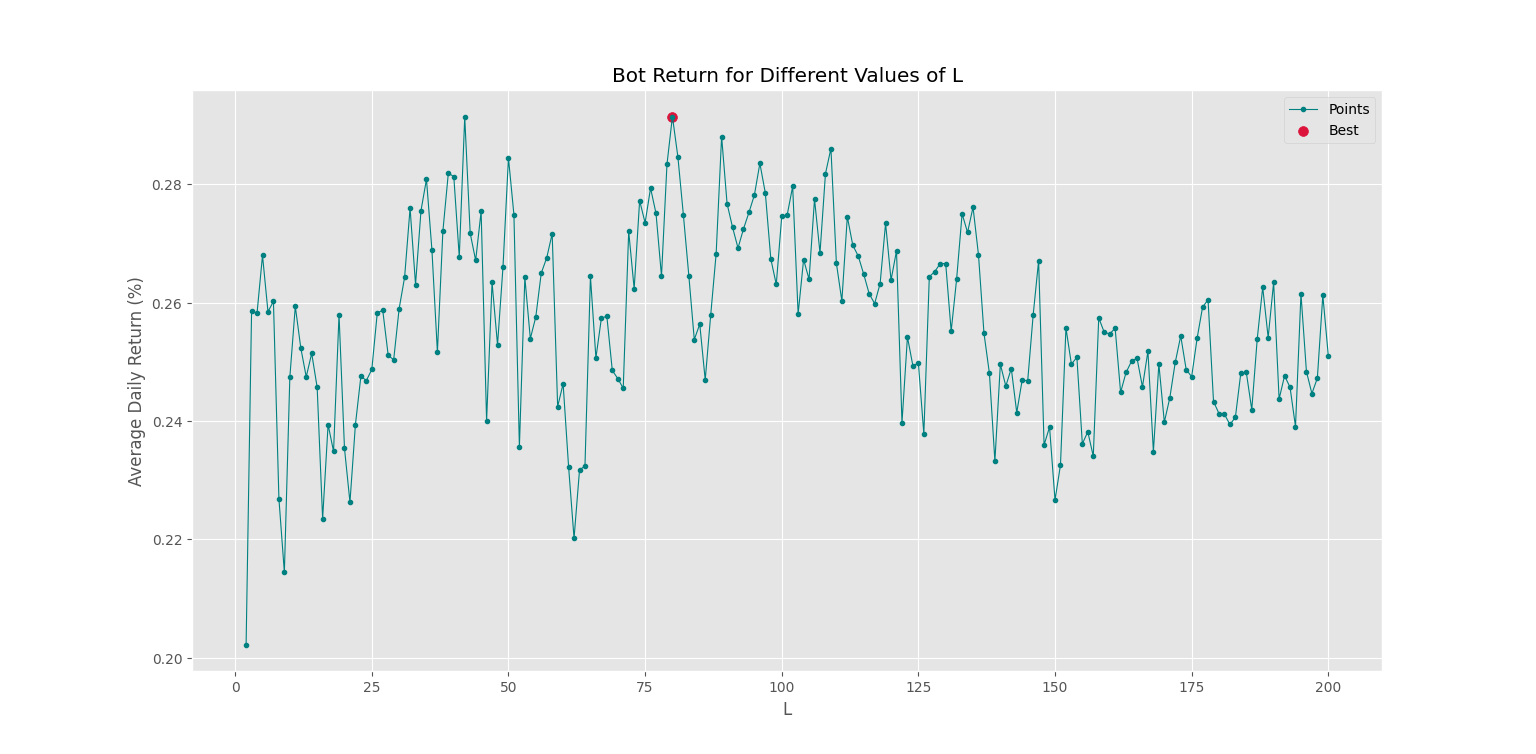
به این ترتیب، مشاهده میکنیم که این استراتژی به ازای تمامی Lها سودده است. همچنین، کمترین و بیشترین میانگین درصد سود روزانه به ترتیب مربوط به L=2 و L=80 است. توجه داشته باشید که L=41 نیز اختلاف ناچیزی با L=80 دارد. نکته مهم دیگر که باید به آن توجه کرد، اهمیت Ld است. طول میانگین متحرک ساده مربوط به خط D در سیگنال حاصل اثرگذار است، به همین دلیل با تغییر Ld نمودار فوق نیز تغییر خواهد کرد.
حال میتوانیم نمودار مربوط به قیمت در مقابل ارزش پرتفوی را نیز رسم کنیم:
Trader.PlotValue('Train')
Trader.PlotValue('Test')
که دو نمودار حاصل خواهد شد. نمودار اول بهصورت زیر است.
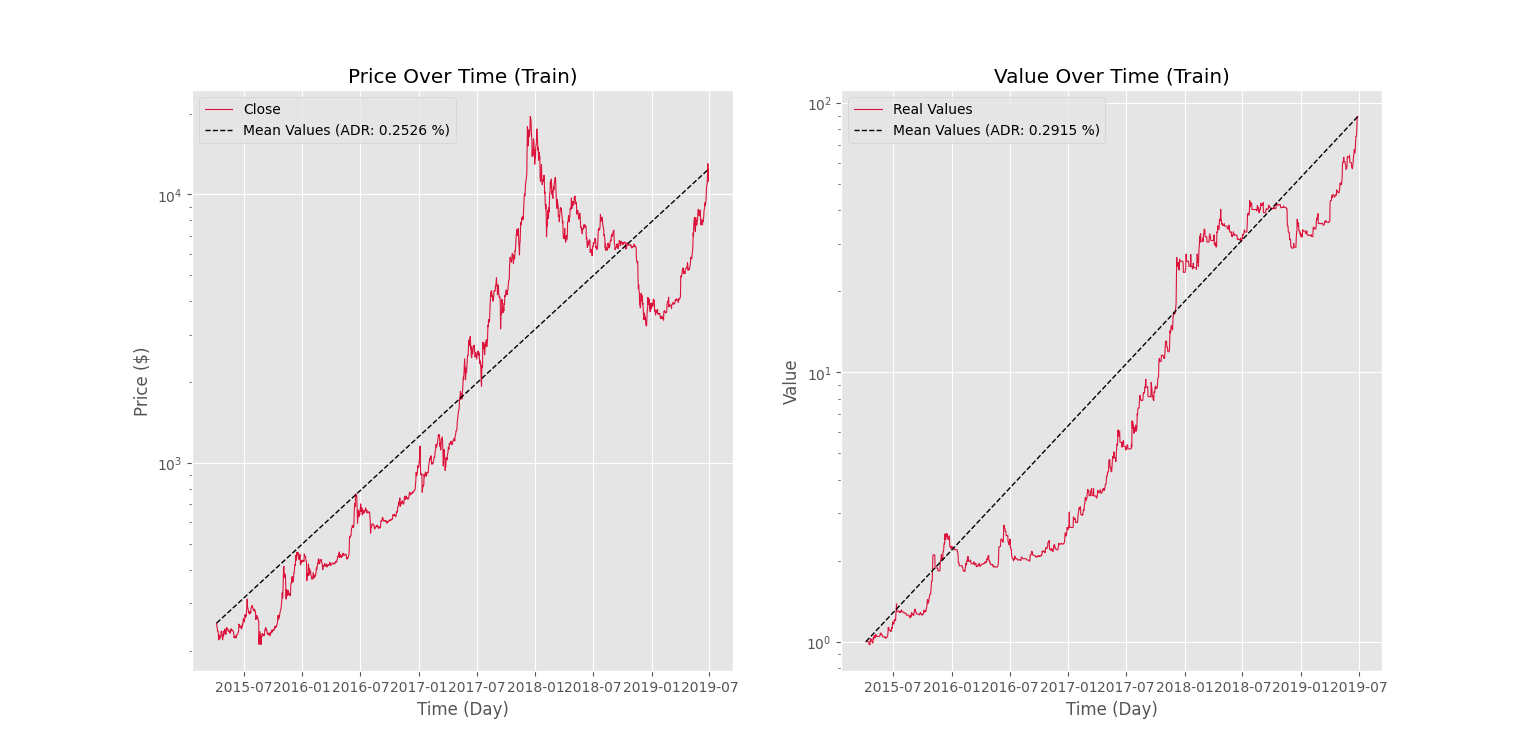
نمودار بعدی بهشکل زیر است.
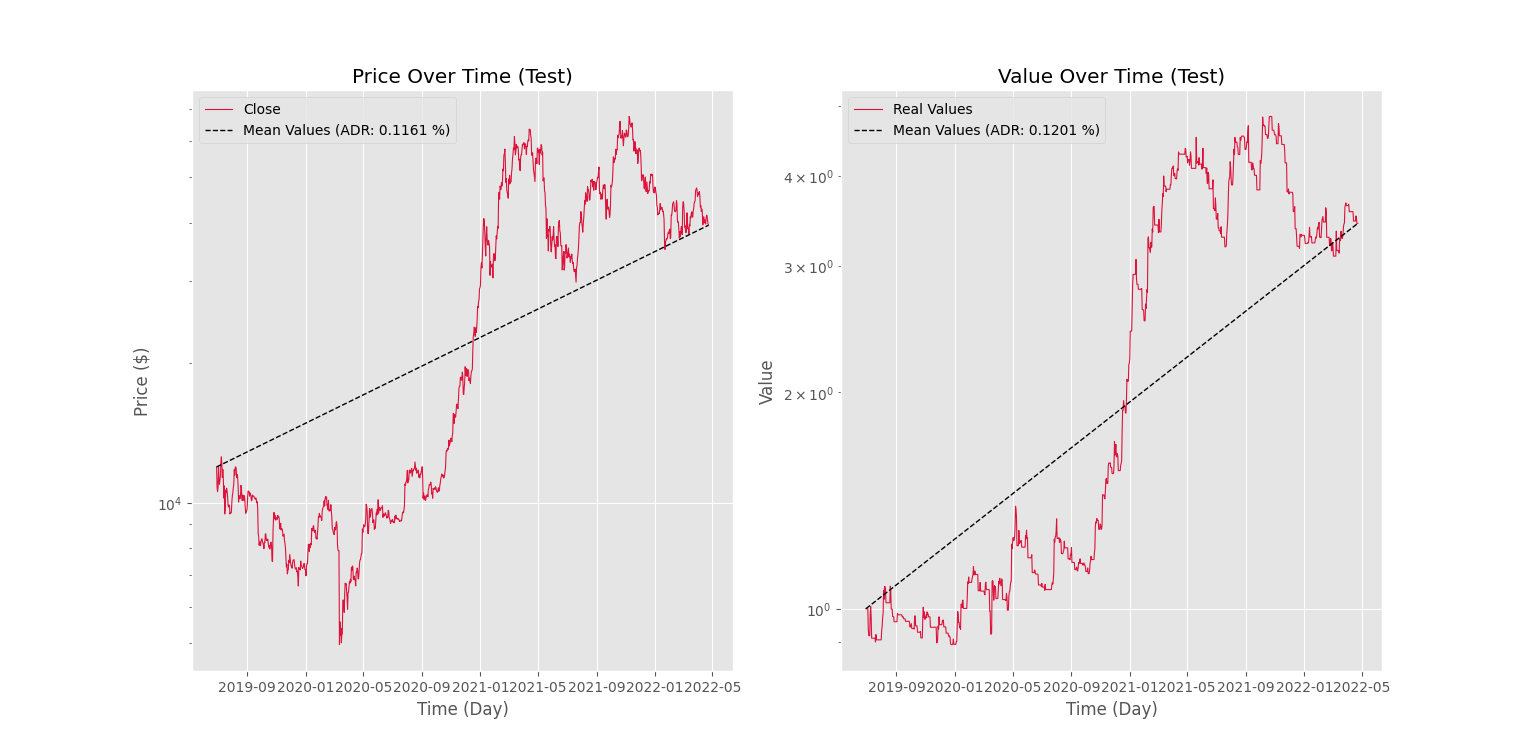
به این ترتیب، مشاهده میکنیم که ربات روی مجموعه داده آموزش به میانگین درصد سود روزانه 0.2915 % رسیده که نسبت به رسد خود نماد اندکی بهتر است. روی مجموعه داده آزمایش نیز ربات به میانگین درصد سود روزانه 0.1201 % رسیده است که شاید در نگاه اول مناسب نباشد، اما با در نظر گرفتن عملکرد نماد در مجموعه داده آزمایش، میتوان به این نتیجه رسید که ربات با توجه به شرایط موجود، عملکرد مناسب خود را حفظ کرده است. اگر نسبت میانگین درصد سود روزانه ربات با به میانگین درصد سود نماد حساب کنیم، خواهیم داشت:
$$begin{aligned}
&text { Train }=frac{0.2915}{0.2526}=1.15 \
&text { Test }=frac{0.1201}{0.1161}=1.03
end{aligned}$$
به این ترتیب، عملکرد مثبت ربات قابل مشاهده است.
حال، آخرین نمودار که برای سیگنال و نقاط خرید و فروش هست را رسم میکنیم:
Trader.PlotSignal('Train')
Trader.PlotSignal('Test')
که در نتیجه آن، شکلهای زیر را خواهیم داشت. نمودار اول به صورت زیر است.
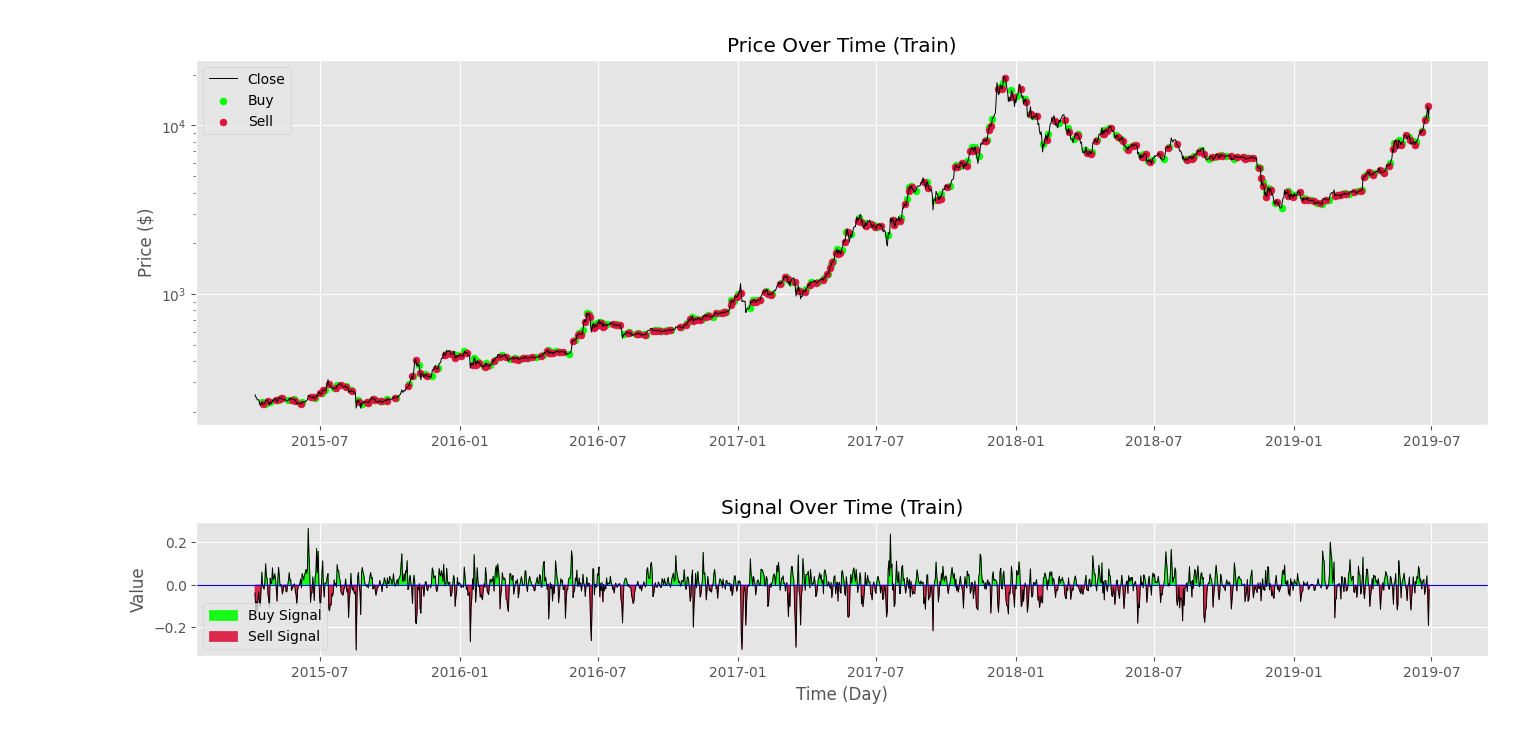
نمودار دوم نیز در ادامه آورده شده است.
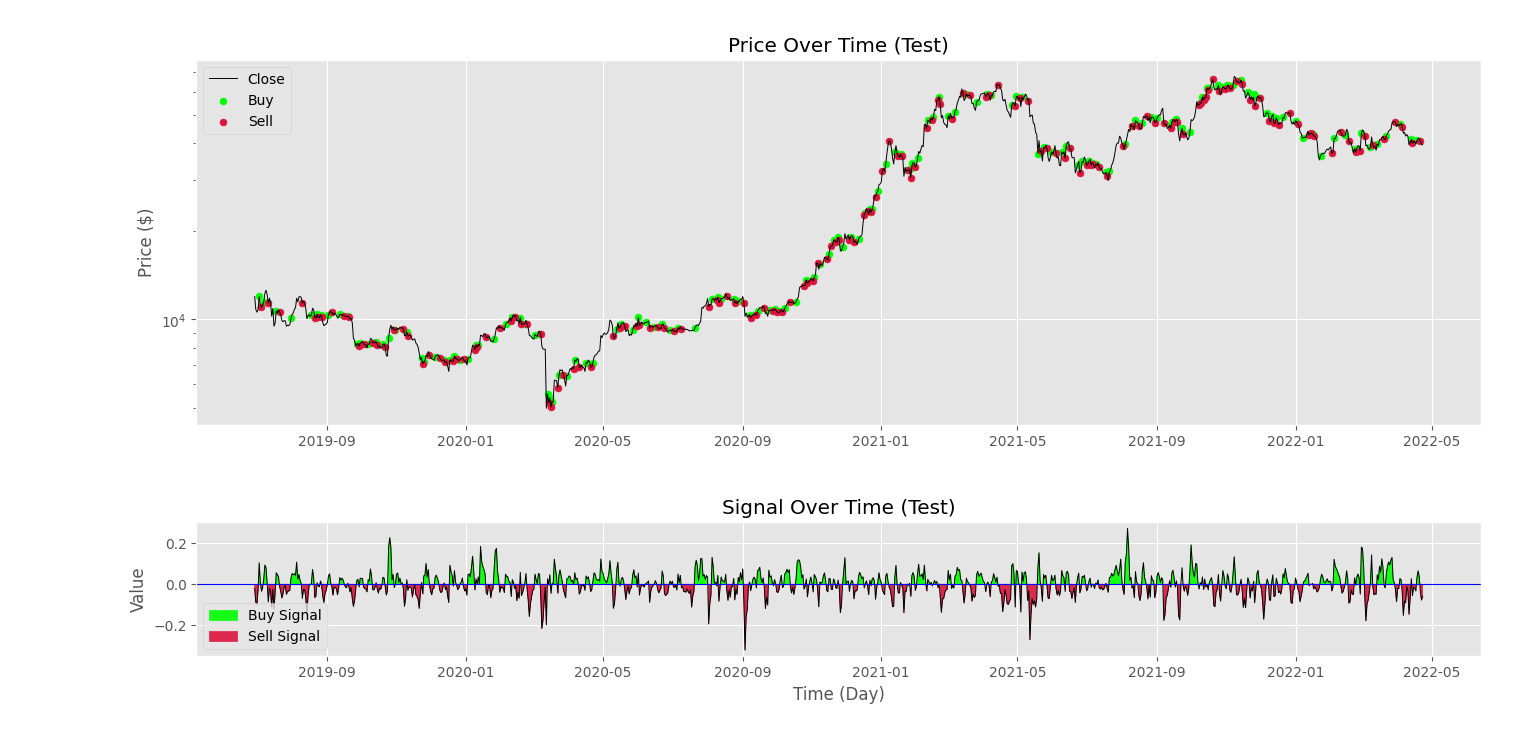
با توجه به استفاده از روش سیگنالگیری به کمک میانگین متحرک، سیگنالهای فراوانی از اندیکاتور دریافت میشود که در نتیجه آن معاملات با فرکانس بالاتری انجام میشوند.
نکته مهم دیگری که باید به آن پرداخت، نرخ بُرد (Win Rate) است. این معیار نشاندهنده نسبت تعداد معاملات برنده به کل معاملات است. برای محاسبه این معیار میتوانیم یک تابع ایجاد کنیم که در ورودی دیکشنری مربوط به نقاط خرید و نقاط فروش را دریافت میکند:
def WR(Buys:dict, Sells:dict):حال، یک متغیر برای ذخیره تعداد معاملات و تعداد معاملات موفق ایجاد میکنیم:
def WR(Buys:dict, Sells:dict):
nT = 0
nW = 0
اکنون یک حلقه ایجاد میکنیم و تعداد معاملات را بهروز (Update) میکنیم:
def WR(Buys:dict, Sells:dict):
nT = 0
nW = 0
for b, s in zip(Buys['Price'], Sells['Price']):
nT += 1
if s > b:
nW += 1
در نهایت نیز نسبت را محاسبه میکنیم و برمیگردانیم:
def WR(Buys:dict, Sells:dict):
nT = 0
nW = 0
for b, s in zip(Buys['Price'], Sells['Price']):
nT += 1
if s > b:
nW += 1
wr = 100 * nW / nT
return wr
بدین صورت، این تابع کامل میشود. این تابع را در انتهای متد Trade استفاده میکنیم:
def Trade(self, DF:pd.core.frame.DataFrame, L:int):
nD = len(DF)
Moneys = np.zeros(nD)
Shares = np.zeros(nD)
Values = np.zeros(nD)
Signals = np.zeros(nD)
Buys = {'Time':[], 'Price':[]}
Sells = {'Time':[], 'Price':[]}
money = 1
share = 0
for i in range(nD):
fp = DF['FP'][i]
signal = DF[f'Signal({L})'][i]
if signal > 0 and share == 0:
share = money / fp
money = 0
Buys['Time'].append(i)
Buys['Price'].append(fp)
elif signal 0:
money = share * fp
share = 0
Sells['Time'].append(i)
Sells['Price'].append(fp)
Moneys[i] = money
Shares[i] = share
Values[i] = money + share * fp
Signals[i] = signal
Return = 100 * ((Values[-1] / Values[0])**(1 / (nD - 1)) - 1)
wr = WR(Buys, Sells)
return Moneys, Shares, Values, Signals, Buys, Sells, wr, Return
به این ترتیب، این متد در هر بار اجرا، نرخ بُرد را نیز برخواهد گرداند. توجه داشته باشید که به دلیل تغییر در خروجیهای متد Trade باید در مواردی که این متد فراخوانی شده، اصلاحاتی انجام شود تا شاهد بروز خطا در کد نباشم.
اکنون برای دریافت نرخ بُرد میتوانیم بنویسیم:
_, _, _, _, _, _, trWR, _ = Trader.Trade(Trader.trDF, Trader.L)
_, _, _, _, _, _, teWR, _ = Trader.Trade(Trader.teDF, Trader.L)
print(f'Train Win Rate: {round(trWR, 2)} %')
print(f'Test Win Rate: {round(teWR, 2)} %')
پس از اجرا خواهیم داشت:
Train Win Rate: 47.66 % Test Win Rate: 37.25 %
به این ترتیب، مشاهده میکنیم که نرخ بُرد معاملات کم است و در مجموعه داده آزمایش کمتر نیز شده که به دلیل ضعیف شدن روند صعودی است. دلیل اصلی کم بودن نرخ بُرد، فرکانس بالای معاملات است. با اینکه ربات سود خوبی از معاملات گرفته است، ولی اغلب معاملات با ضرر بسته شدهاند. بنابراین، میتوان با راحتی متوجه شد که اغلب معاملاتی که با شکست روبهرو شدهاند، ضررهای کوچکی داشتهاند.
میتوان تنظیم L را با استفاده از نرخ بُرد نیز انجام داد، اما باید توجه داشته که ممکن است به اندازه میانگین درصد سود روزانه کاربردی نباشد.
جمعبندی
در این مطلب توانستیم یک ربات معاملهگر بر پایه اسیلاتور استوکستیک ایجاد کنیم و نتایج آن را به شکل نمودار و اعداد نشان دهیم. برای مطالعه بیشتر در این باره، میتوان موارد زیر را بررسی کرد:
- اندیکاتور استوکستیک RSI (Stochastic RSI) چیست و چه مزایایی دارد؟
- چگونه از انجام معاملات فراوان توسط ربات جلوگیری کنیم؟
- چرا پیادهسازی متدهای رسم نمودار به شکل متد، میتواند بهتر از پیادهسازی آنها به شکل تابع باشد؟
- کد ربات را بهگونهای تغییر دهید که علاوه بر بهینهسازی، مقدار را نیز بهینه کند.
- تابع بهینهساز Brute را از کتابخانه Scipy مطالعه کرده و شباهت آن به فرایند پیادهسازی شده در برنامه را بیابید.

