روش گوس سایدل در متلب — از صفر تا صد + آموزش کدنویسی

در آموزشهای پیشین مجله تم آف، با روش گوس سایدل آشنا شدیم. در این آموزش، میخواهیم به پیادهسازی آن بپردازیم و روش گوس سایدل در متلب را بررسی کنیم.

روش گوس سایدل یک روش تکراری متداول و پرکاربرد برای حل دستگاه معادلات خطی جبری است. این روش برای هر ماتریس همگرا با درایههای غیرصفر قطری قابل استفاده است. این روش از نام دو ریاضیدان آلمانی به نام »کارل فریدریش گوس» (Carolus Fridericus Gauss) و «فیلیپ لودویگ فون سایدل» (Philipp Ludwig von Seidel) گرفته شده است.
گاوس سایدل نسخه تصحیحشده روش گاوس ژاکوبی است. در این روش، مانند هر روش تکراری دیگر، حل تقریبی معادلات در نظر گرفته میشود و تا حصول درجه دقت مطلوب، تکرار انجام میشود.
در آموزشهای قبلی، الگوریتم روش گوس سایدل را بررسی کردیم. در این مطلب قصد داریم پیادهسازی روش گوس سایدل در متلب را انجام دهیم. اما پیش از آن، این روش را مرور میکنیم و مورد بحث قرار دهیم و پس از آن برنامه متلب را با مثالهای عددی ارائه میکنیم.
پیاده سازی روش گوس سایدل در متلب: مثال اول
در اینجا، مفاهیم ریاضی مختصری از روش گوس سایدل را مرور کنیم. ماتریسها، تکرارها و روشی که در زیر توضیح داده شده است، دستورالعملهای اساسی برای نوشتن کد برنامه برای روش گاوس-سیدل در متلب را پوشش میدهد.
دستگاه معادلات خطی زیر را در نظر بگیرید:
$$ begin {aligned}
& a _ { 1 1 } x _ { 1 } + a _ { 1 2 } x _ { 2 } + a _ { 1 3 } x _ { 3 } + a _ { 1 4 } x _ { 4 } + a _ { 1 5 } x _ { 5 } + a _ { 1 6 } x _ { 6 } ldots ldots + a _ { 1 n } x _ { n } = b_ { 1 } \
& a _ { 2 1 } x _ { 1 } + a _ { 2 2 } x _ { 2 } + a _ { 2 3 } x _ { 3 } + a _ { 24 } x _ { 4 } + a _ { 2 5 } x _ { 5 } + a _ { 2 6 } x _ { 6 } ldots ldots + a _ { 2 n } x _ { n } = b _ { 2 } \
& a _ { 3 1 } x _ { 1 } + a _ { 32 } x _ { 2 } + a _ { 3 3 } x _ { 3 } + a _ { 3 4 } x _ { 4 } + a _ { 3 5 } x _ { 5 } + a _ { 3 6 } x _ { 6 } ldots ldots . + a _ { 3 n } x _ { n } = b _ { 3 } \
& a _ {n 1} x _ { 1 } + a _ { n 2 } x _ { 2 } + a _ {n 3 } x _ { 3 } + a _ { n 4 } x _ { 4 } + a _ { n 5 } x _ { 5 } + a _ { n 6 } x _ { 6 } ldots ldots + a _ { n n } x _ { n } = b _ { n }
end {aligned} $$
که در آن، $$a_{ij}$$ ضریب عبارات مجهول $$x_i$$ را نشان میدهد.
معادلات فوق را میتوان به صورت ماتریسی زیر ارائه کرد:
$$ A = left [ begin {array} {cccc}
a _ { 1 1 } & a _ { 1 2 } & cdots & a _ { 1 n } \
a _ { 2 1 } & a _ { 2 2 } & cdots & a _ { 2 n } \
vdots & vdots & ddots & vdots \
a _ { n 1 } & a _ { n 2 } & cdots & a _ { n n }
end{array} right], quad mathbf { x } = left [begin{array}{ c }
x _ { 1 } \
x _ { 2 } \
vdots \
x _ { n }
end {array} right ] , quad mathbf { b } = left [ begin {array} { c }
b _ { 1 } \
b _ { 2 } \
vdots \
b _ { n }
end {array} right] $$
یا بهسادگی میتوان آن را بهصورت زیر نوشت:
$$ [A][X] = [B] $$
حال، با تجزیه ماتریس $$A$$ به دو بخش پایینمثلثی و بالامثلثی، بهدست میآوریم:
$$ A = L times U $$
که در آن،
$$ L _ {*} = left [ begin {array} {cccc}
a _ { 1 1 } & 0 & cdots & 0 \
a _ { 2 1 } & a _ { 2 2 } & cdots & 0 \
vdots & vdots & ddots & vdots \
a _ { n 1 } & a _ { n 2 } & cdots & a _ { n n }
end {array}right] , quad U = left [ begin {array} {cccc}
0 & a _ { 1 2 } & cdots & a _ { 1 n } \
0 & 0 & cdots & a _ { 2 n } \
vdots & vdots & ddots & vdots \
0 & 0 & cdots & 0
end {array} right] $$
علاوه بر این، دستگاه معادلات خطی را میتوان بهصورت زیر بیان کرد:
$$ L times X = B – UX qquad (*) $$
در روش گوس سایدل، معادله (*) بهصورت مکرر با حل مقدار سمت چپ $$X $$ و سپس با استفاده از $$X$$ قبلی بهدستآمده در سمت راست حل میشود. از نظر ریاضی، فرایند تکرار در روش گوس سایدل را میتوان بهصورت زیر بیان کرد:
$$ X ^ { ( k + 1 ) } = L ^ { – 1 } left ( B – U X ^ { ( k ) } right ) $$
با اعمال جایگزینی رو به جلو، عناصر $$X(k+1)$$ را می توان به صورت زیر محاسبه کرد:
$$ x _ { i } ^ { ( k + 1 ) } = frac { 1 } { a _ { i i } } left ( b _ { i } – sum _ { j i } a _ { i j } x _ { j } ^ { ( k ) } right ) , quad i , j = 1 , 2 , ldots , n . $$
روال فوق برای این روش در برنامه متلب پیادهسازی میشود. روند تکرار تا زمانی ادامه مییابد که مقادیر مجهولات زیر حد خطای مطلوب قرار گیرند.
برای آشنایی با نرمافزار متلب، پیشنهاد میکنیم به مجموعه آموزش نرم افزار متلب (MATLAB) تم آف مراجعه کنید که لینک آن در ادامه آورده شده است.
- برای مشاهده مجموعه آموزش نرم افزار متلب (MATLAB) + اینجا کلیک کنید.
کد زیر، تابعی است که ماتریسهای A و B را میگیرد و جواب x را ارائه میدهد.
% Gauss-Seidel Method in MATLAB
function x = gauss_siedel( A ,B )
disp ( 'Enter the system of linear equations in the form of AX=B')
%Inputting matrix A
A = input ( 'Enter matrix A : n')
% check if the entered matrix is a square matrix
[na , ma ] = size (A);
if na ~= ma
disp('ERROR: Matrix A must be a square matrix')
return
end
% Inputting matrix B
B = input ( 'Enter matrix B : ')
% check if B is a column matrix
[nb , mb ] = size (B);
if nb ~= na || mb~=1
disp( 'ERROR: Matrix B must be a column matrix')
return
end
% Separation of matrix A into lower triangular and upper triangular matrices
% A = D + L + U
D = diag(diag(A));
L = tril(A)- D;
U = triu(A)- D
% check for convergence condition for Gauss-Seidel method
e= max(eig(-inv(D+L)*(U)));
if abs(e) >= 1
disp ('Since the modulus of the largest Eigen value of iterative matrix is not less than 1')
disp ('this process is not convergent.')
return
end
% initial guess for X..?
% default guess is [ 1 1 .... 1]
r = input ( 'Any initial guess for X? (y/n): ','s');
switch r
case 'y'
% asking for initial guess
X0 = input('Enter initial guess for X :n')
% check for initial guess
[nx, mx] = size(X0);
if nx ~= na || mx ~= 1
disp( 'ERROR: Check input')
return
end
otherwise
X0 = ones(na,1);
end
% allowable error in final answer
t = input ( 'Enter the error allowed in final answer: ');
tol = t*ones(na,1);
k= 1;
X( : , 1 ) = X0;
err= 1000000000*rand(na,1);% initial error assumption for looping
while sum(abs(err) >= tol) ~= zeros(na,1)
X ( : ,k+ 1 ) = -inv(D+L)*(U)*X( : ,k) + inv(D+L)*B;% Gauss-Seidel formula
err = X( :,k+1) - X( :, k);% finding error
k = k + 1;
end
fprintf ('The final answer obtained after %g iterations is n', k)
X( : ,k)در کد بالا، ابتدا یک تابع x = gauss_siedel(A,B) تعریف شده است. در اینجا، A و B ماتریسهایی هستند که با ضرایب استفاده شده در سیستم خطی معادلات ایجاد میشوند. عناصر A و B طبق دستور اولیه برنامهنویسی متلب به برنامه وارد میشوند. دقت کنید که A و B باید ابعاد مناسبی داشته باشند. A باید یک ماتریس مربعی و B باید یک ماتریس ستونی باشد تا معیارهای روش گوس سایدل را برآورده کند. سپس، همانطور که توضیح داده شد، ماتریس A به قسمتهای بالامثلثی و پایینمثلثی تقسیم میشود تا مقدار تکرار اول بهدست آید.
مقدار متغیرهای بهدستآمده از تکرار اول برای شروع تکرار دوم استفاده میشود و برنامه به تکرار ادامه میدهد تا زمانی که جواب به زیر خطای مطلوب کاربر ارائه برسد.
نمونه خروجی پیاده سازی این کد روش گوس سایدل در متلب بهصورت زیر است:
Enter matrix A : [4 -1 -1 ; -2 6 1 ; -1 1 7] A = 4 -1 -1 -2 6 1 -1 1 7 Enter matrix B : [3 ; 9 ; -6] B = 3 9 -6 U = 0 -1 -1 0 0 1 0 0 0 Any initial guess for X? (y/n): 1 Enter the error allowed in final answer: 0.005 The final answer obtained after 6 iterations is ans = 1.0000 2.0000 -1.0000
معادلات مثال بالا عبارتاند از:
$$ begin{align}
4 x_{1}-x_{2}-x_{3} & =3 \
-2 x_{1}+6 x_{2}+x_{3} & =9 \
-x_{1}+x_{2}-7 x_{3} & =-6
end{align} $$
برای بهدست آوردن مقدار تکرار اول، معادلات دادهشده را بهصورت زیر مینویسیم:
$$ begin{align}
4x_1 – 0 –0 & =3 \
-2x_1 + 6x_2 + 0 & =9 \
-x_1 + x_2 – 7x_3 & =-6
end{align} $$
- از معادله اول $$x_1 = frac 34 = 0.750 $$ بهدست میآید.
- این مقدار $$x_1$$ را در معادله دوم جایگذاری میکنیم: $$ x_ 2 = frac {[9 + 2(0.750)]}{ 6} = 1.750 $$.
- مقادیر $$x_1$$ و $$x_ 2 $$ را در معادله سوم جایگذاری میکنیم: $$ x_ 3 = frac {[-6 + 0.750 − 1.750]}{ 7} = − 1.000 $$.
- بنابراین، نتیجه تکرار اول $$ ( 0.750, 1.750, -1.000 ) $$ است.
تکرارهای بیشتر در جدول زیر ارائه شده است که در آن، k تعداد تکرار است.
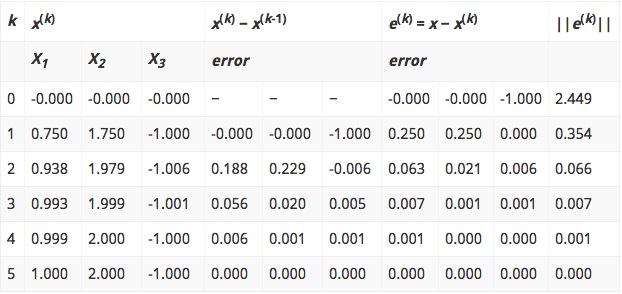
میبینیم که جواب نهایی $$(1.000, 2.000, -1.000)$$ است.
پیاده سازی روش گوس سایدل در متلب: مثال دوم
دیدیم که در روش گوس سایدل، دستگاه معادلات با استفاده از جایگزینی رو به جلو حل میشود، به طوری که هر بخش از آخرین مقدار بهدستآمده برای بخش قبلی استفاده میکند. این کار متفاوت از روش ژاکوبی است که در آن تمام اجزای یک تکرار بر اساس تکرار قبلی محاسبه میشوند. اکنون یک مثال دیگر از پیادهسازی روش گوس سایدل در متلب را بررسی میکنیم. یک دستگاه معادلات خطی $$Ax=b$$ با اندازه $$n$$ را میتوان به صورت زیر نوشت:
$$ left ( begin {array} {cccc}
a _ { 1 1 } & a _ { 1 2 } & cdots & a _ { 1 n } \
a _ { 2 1 } & a _ { 2 2 } & cdots & a _ { 2 n } \
vdots & vdots & vdots & vdots \
a _ { n 1 } & a _ { n 2 } & cdots & a _ { n n }
end {array} right ) left ( begin {array} {c}
x _ { 1 } \
x _ { 2 } \
vdots \
x _ { n }
end{array} right ) = left ( begin {array} {c}
b _ { 1 } \
b _ { 2 } \
vdots \
b _ { n }
end {array} right ) $$
سمت چپ معادله بالا را میتوان اینگونه نوشت:
$$ left ( begin {array} {cccc}
0 & a _ { 1 2 } & cdots & a _ { 1 n } \
0 & 0 & cdots & a _ { 2 n } \
vdots & vdots & vdots & vdots \
0 & 0 & cdots & 0
end {array} right ) left ( begin {array} {c}
x _ { 1 } \
x _ { 2 } \
vdots \
x _ { n }
end {array} right ) + left ( begin {array} {cccc}
a _ { 1 1 } & 0 & cdots & 0 \
a _ { 2 1 } & a _ { 2 2 } & cdots & 0 \
vdots & vdots & vdots & vdots \
a _ { n 1 } & a _ { n 2 } & cdots & a _ { n n }
end {array} right ) left ( begin {array} { c }
x _ { 1 } \
x _ { 2 } \
vdots \
x _ { n }
end {array} right ) = left ( begin {array} { c }
b _ { 1 } \
b _ { 2 } \
vdots \
b _ { n }
end {array} right ) $$
ماتریس $$A$$ را به دو ماتریس جدا کردهایم ($$A=U+L$$) که در آن $$U$$ یک ماتریس بالامثلثی با درایههای قطری صفر است، در حالی که $$L$$ یک ماتریس پایینمثلثی است که درایههای قطری آن برابر با درایههای قطری $$A$$ است. اگر با درایههای قطری غیرصفر $$A$$ شروع میکنیم، سپس میتوان از $$L$$ برای حل دستگاه با روش جایگزینی رو به جلو استفاده کرد:
$$ A x = b Rightarrow (U+L)x=bRightarrow Lx=b-Ux$$
همان معیار توقف روش ژاکوبی را میتوان برای روش گوس سایدل نیز استفاده کرد.
آنچه را که گفتیم، با یک مثال شرح میدهیم و در متلب پیادهسازی میکنیم. دستگاه معادلات زیر بهصورت $$Ax=b$$ داده شده است:
$$ left ( begin {array} {ccc}
3 & -0.1 & -0.2 \
0.1 & 7 & -0.3 \
0.3 & -0.2 & 10
end{array} right ) left ( begin{array} {c}
x _ { 1 } \
x _ { 2 } \
x _ { 3 }
end {array}right) = left ( begin {array} {c}
7.85 \
-19.3 \
71.4
end {array} right) $$
معیار توقف $$ varepsilon_S = 0.0001$$ را در نظر میگیریم. ابتدا معادلات را بهصورت زیر بازنویسی میکنیم:
$$ left ( begin {array} {ccc}
3 & 0 & 0 \
0.1 & 7 & 0 \
0.3 & -0.2 & 10
end {array} right ) left ( begin {array} { l }
x _ { 1 } \
x _ { 2 } \
x _ { 3 }
end {array} right ) = left ( begin {array} { c }
7 . 8 5 \
– 1 9 . 3 \
7 1 . 4
end {array} right ) – left ( begin {array} {ccc}
0 & – 0 . 1 & – 0 . 2 \
0 & 0 & -0.3 \
0 & 0 & 0
end {array} right ) left ( begin {array} { l }
x _ { 1 } \
x _ { 2 } \
x _ { 3 }
end {array} right ) $$
سپس، حدسهای اولیه برای درایههای $$x_1^{(0)}=1$$ ، $$x_2^{(0)}=1$$، $$x_3^{(0)}=1$$ برای محاسبه برآوردهای جدید با استفاده از جایگزینی رو به جلو استفاده میشود. توجه داشته باشید که در جایگزینی رو به جلو، مقدار $$x_2^{(1)}$$ از مقدار $$x_1^{(1)}$$ استفاده میکند و $$x_3^{(1)}$$ از مقادیر $$x_1^{(1)}$$ و $$x_2^{(1)}$$ استفاده میکند:
$$ begin {split} 3 x _ 1 ^ { ( 1 ) } = 7 . 8 5 + 0 . 1 ( 1 )+ 0 .2 ( 1 ) Rightarrow x _ 1 ^ { (1 ) } = 2.7 1 6 6 6 7 \0.1 x _ 1 ^ { ( 1 )} + 7x _ 2 ^ { ( 1 ) } = – 1 9 .3 + 0 . 3 ( 1 ) Rightarrow x _ 2 ^ { ( 1 ) } = – 2.7531 \ 0.3 x _ 1 ^ { ( 1 ) } – 0 . 2 x _ 2 ^ { ( 1) } + 1 0 x _ 3 ^{ ( 1 ) } = 7 1. 4 Rightarrow x _ 3 ^ { ( 1 ) } = 7 . 0 0 3 4 4 end {split} $$
خطای تقریبی نسبی در این مورد برابر است با
$$ varepsilon _ r = frac { sqrt { ( 2.716667-1 ) ^ 2 + ( – 2.7531 – 1 ) ^ 2 + ( 7.00344-1 ) ^ 2 } } { sqrt { 2.716667 ^ 2 +( – 2 .7531 ) ^ 2 + 7 . 0 0 34 4^ 2 } } = 0 . 9 1> varepsilon_s$$
برای تکرار دوم، داریم:
$$ begin{split}3x_1^{(2)}=7.85+0.1(-2.7531)+0.2(7.00344)Rightarrow x _ 1 ^ { ( 2 ) } = 2.99179 \ 0 . 1 x _ 1 ^ { ( 2 ) } + 7 x _ 2 ^ { ( 2 ) } = -19.3+0.3(7.00344)Rightarrow x_2^ { ( 2 ) } = – 2 . 4 9 9 7 4 \0.3x_1^{(2)}-0.2x_2^{(2)}+10x_3^{(2)}=71.4Rightarrow x _ 3 ^ { ( 2 ) } = 7. 00 0 2 5 end {split} $$
خطای تقریبی نسبی در این مورد برابر است با
$$ varepsilon _ r = frac { sqrt { ( 2.99179-2.716667) ^ 2 + ( -2.49974+2.7531 ) ^ 2 + ( 7.00025-7.00344)^2}}{sqrt{2.99179^2+(-2.49974)^2 + 7 . 0 0 0 2 5 ^ 2}}=0.047>varepsilon_s $$
برای تکرار سوم، خواهیم داشت:
$$ begin{split}3x_1^{(3)}=7.85+0.1(-2.49974)+0.2(7.00025)Rightarrow x_1^{(3)}=3.00003\0.1x_1^{(3)}+7x_2^{(3)}=-19.3+0.3(7.00025)Rightarrow x_2^{(3)}=-2.49999\0.3x_1^{(3)}-0.2x_2^{(3)}+10x_3^{(3)}=71.4Rightarrow x_3^{(3)}=7.end {split} $$
خطای تقریبی نسبی نیز برابر است با
$$ varepsilon_r=frac{sqrt{(3.00003-2.99179)^2+(-2.49999+2.49974)^2+(7.-7.00025)^2}}{sqrt{3.00003^2+(-2.49999)^2+7.^2}}=0.00103>varepsilon_s $$
تکرار چهارم نیز بهصورت زیر است:
$$ begin {split} 3 x_ 1 ^ { ( 4 ) } = 7 . 8 5 + 0. 1 (- 2 . 4 99 9 9 ) + 0 . 2 ( 7 ) Rightarrow x _ 1^ { ( 4 ) } = 3 . \ 0 . 1 x_ 1 ^{ ( 4 ) } + 7 x _ 2 ^{ ( 4 ) } = – 19 . 3 + 0 .3 ( 7 . ) Rightarrow x _ 2 ^{ ( 4 ) }= – 2 . 5 \ 0 . 3x _1 ^ { ( 4) } – 0. 2 x _2 ^{ ( 4 )} + 1 0x _ 3^ { ( 4) } = 7 1 . 4 Rightarrow x _ 3 ^ { ( 4 )} = 7 . end{split}$$
و خطای آن برابر است با
$$ varepsilon_r=frac{sqrt{(3.-3.00003)^2+(-2.5+2.49999)^2+(7.-7.)^2}}{sqrt{3^2+(-2.5)^2+7.^2}}=3.4times 10^{-6}
بنابراین، دستگاه معادلات پس از چهار تکرار همگرا میشود.
با روش جایگذاری رو به جلو در معادله $$ Lx^{(k+1)}=b-Ux^{(k)}$$، میتوان $$i$$اُمین درایه $$ x _ i ^ {(k+1)}$$ در تکرار $$ k+1 $$ را بهصورت زیر محاسبه کرد:
$$ begin{equation*}x_i^{(k+1)}=frac{b_i-sum_{j=i+1}^nA_{ij}x_j^{(k)}-sum_{j=1}^{i-1}A_{ij}x_j^{(k+1)}}{A_{ii}}end{equation*} $$
مثال کد MATLAB زیر برای تأکید بر رویکرد این مثال است و با $$L$$ و $$U$$ کار میکند. با این حال، الگوریتم را میتوان فشردهتر نوشت، مثلاً میتوان از فرمول اخیر استفاده کرد. دقت کنید که برنامه زیر برای حداکثر ۱۰۰ تکرار و خطای ۰٫۰۰۰۱ نوشته شده است.
function x = gauss_seidel(A,b,x0)
% Function to demonstrate the Gauss-Seidel method to solve a system Ax=b
%
% A is nxn matrix of coefficients
% b is nx1 column vector of constants
% xo is nx1 column vector of the initial guess
% x is the solution (nx1 column)
%
% Syntax: x = gauss_seidel(A,b,x0)
clc
[rA,cA] = size(A); % Determine the size of A
[rb,cb] = size(b); % Determine the size of b
% Input checks
if rA ~= cA
disp('Error: A is not a square matrix')
return
else
n = rA;
end
if cb ~= 1
disp('Error: b is not a column vector')
return
end
if cA ~= rb
disp('Error: Matrix and vector dimensions are not compatible')
return
end
dA = det(A);
if dA == 0
disp('Error: Matrix is singular')
return
end
% Initialize the variables
maxit = 100;
es = 0.0001;
er = 1;
xnew = x0;
count = 0;
% Prepare U and L matrices
U = zeros(n);
for i=1:n
for j = i+1:n
U(i,j)=A(i,j);
end
end
L = A - U;
% For display only
outmat = zeros(1,n+2);
outmat(1,:) = [count transpose(xnew) er];
% main loop
while(er>es && countبرای استفاده از تابع، ابتدا دستورات زیر را وارد میکنیم:
A = [3 -0.1 -0.2 ; 0.1 7 -0.3 ; 0.3 -0.2 10];
b = [7.85 ; -19.3 ; 71.4];
x0=[1 ; 1 ; 1];
gauss_seidel(A,b,x0);که نتیجه آن، بهصورت زیر خواهد بود:
Gauss-Seidel Method ------------------------------------------------- Output format: First column = iteration number Next columns = estimates of the components of x Last column = er 0 1.0000 1.0000 1.0000 1.0000 1.0000 2.7167 -2.7531 7.0034 0.9106 2.0000 2.9918 -2.4997 7.0003 0.0467 3.0000 3.0000 -2.5000 7.0000 0.0010 4.0000 3.0000 -2.5000 7.0000 0.0000 In 4 iterations, x was found to be: 3.0000 -2.5000 7.0000 er = 3.41268e-06 ans = 3.0000 -2.5000 7.0000
پیاده سازی روش گوس سایدل در متلب: مثال سوم
کد زیر یک روش دیگر برای نوشتن روش گوس سایدل در متلب است. همانطور که در این کد مشخص است، ماتریسها و بردارهای مربوط به دستگاه معادلات و مقدار خطای مطلوب تعیین شده و جواب نهایی در جایی که شرط خطا برآورده شود، نشان داده میشود.
%% Gauss Seidel Method
%% Solution of x in Ax=b using Gauss Seidel Method
% * _*Initailize 'A' 'b' & intial guess 'x'*_
%%
A=[5 -2 3 0;-3 9 1 -2;2 -1 -7 1; 4 3 -5 7]
b=[-1 2 3 0.5]'
x=[0 0 0 0]'
n=size(x,1);
normVal=Inf;
%%
% * _*Tolerence for method*_
tol=1e-5; itr=0;
%% Algorithm: Gauss Seidel Method
%%
while normVal>tol
x_old=x;
for i=1:n
sigma=0;
for j=1:i-1
sigma=sigma+A(i,j)*x(j);
end
for j=i+1:n
sigma=sigma+A(i,j)*x_old(j);
end
x(i)=(1/A(i,i))*(b(i)-sigma);
end
itr=itr+1;
normVal=norm(x_old-x);
end
%%
fprintf('Solution of the system is : n%fn%fn%fn%f in %d iterations',x,itr);خروجی این مثال روش گوس سایدل در متلب بهصورت زیر است:
A = 5 -2 3 0 -3 9 1 -2 2 -1 -7 1 4 3 -5 7 b = -1.0000 2.0000 3.0000 0.5000 x = 0 0 0 0 Solution of the system is : 0.178697 0.230293 -0.477635 -0.470549 in 8 iterations>>
جمعبندی
در این آموزش از مجله تم آف، با برنامهنویسی روش گاوس سایدل در متلب آشنا شدیم و آن را با چند روش متنوع همراه با مثالهای عددی بررسی کردیم.

